ИДЗ 12.1 – Вариант 0.

1. Доказать сходимость ряда и найти его сумму.
1.0
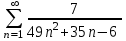
Знаменатель приравняем к нулю, решим квадратное уравнение



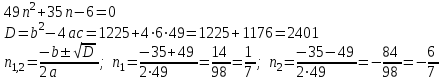
Тогда ряд можно представить в виде



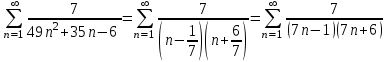
Общий член 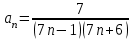данного ряда представим в виде суммы простейших дробей: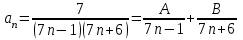



Тогда:

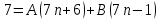
При ;

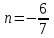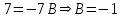
При ;

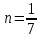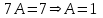
Поэтому

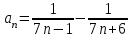
Найдем сумму первых n членов ряда:



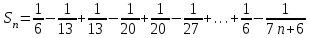
Вычислим сумму ряда:



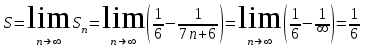
Сумма ряда 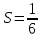, данный ряд сходится

2. Исследовать на сходимость указанные ряды с положительными членами.(2-6)
2.0

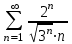
Воспользуемся признаком Д’Аламбера

Пусть для ряда 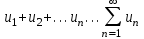, 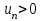(начиная с некоторого n=n₀) и существует предел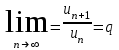

Тогда

1) при q<1 данный ряд сходится;

2) при q>1 данный ряд расходится.

где ,



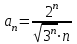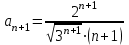
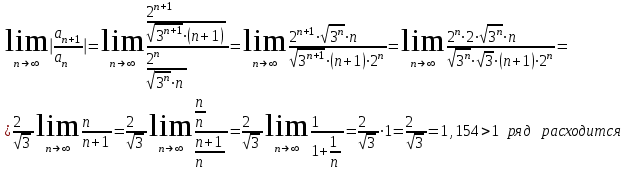
Ответ: ряд расходится


3.0

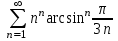
Если, начиная с некоторого n=n

---

₀, u_n > 0 и 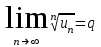, то

при q < 1 ряд сходится, а

при q > 1 ряд расходится

при q = 1 радикальный признак Коши не применим
Согласно радикальному признаку Коши, имеем:



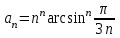
Заменим арксинус эквивалентной величиной



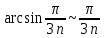
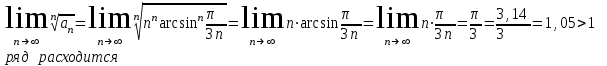
Ответ: ряд расходится

4.0

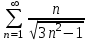
Воспользуемся интегральным признаком Коши.

Для этого исследуем несобственный интеграл:



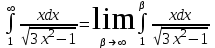
Решим неопределенный интеграл:



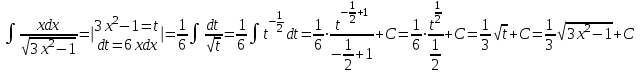
Тогда



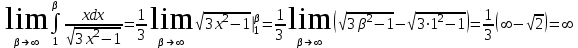
Так как интеграл расходится, следовательно, исследуемый ряд тоже расходится
Ответ: ряд расходится

5.0

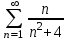
Сравним данный ряд с расходящимся гармоническим рядом .

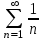Используем предельный признак сравнения



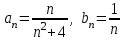
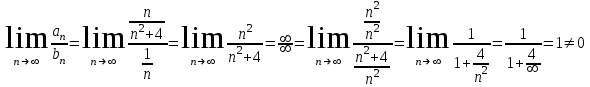
Таким образом, исследуемый ряд расходится вместе с гармоническим рядом

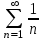
Ответ: ряд расходится

6.0

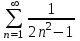
Сравним данный ряд со сходящимся рядом .

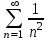Используем предельный признак сравнения


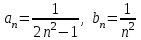
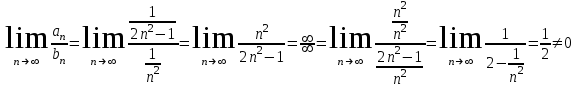
Получено конечное число, отличное от нуля, значит, исследуемый ряд сходится вместе с рядом

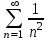
Ответ: ряд сходится

---

Исследовать на сходимость и абсолютную сходимость знакочередующиеся ряды. (7-8)
7.0

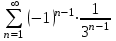
Используем признак Лейбница.

Данный ряд является знакочередующимся.

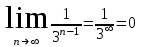- условие выполняется

Ряд сходится по признаку Лейбница.

Исследуем ряд на абсолютную сходимость:



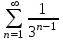
Воспользуемся признаком Д’Аламбера

где ,



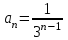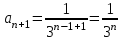
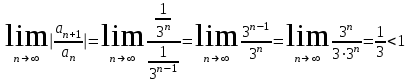
Так как 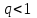, следовательно, исследуемый ряд сходится

Исходный ряд абсолютно сходится
Ответ: ряд абсолютно сходится

8.0

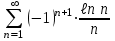
Используем признак Лейбница.

Данный ряд является знакочередующимся.

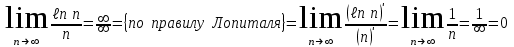- условие выполняется

Ряд сходится по признаку Лейбница.

Исследуем ряд на абсолютную сходимость:



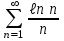
Воспользуемся интегральным признаком Коши.

Для этого исследуем несобственный интеграл:



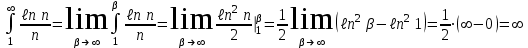
Так как интеграл расходится, следовательно, исследуемый ряд тоже расходится

Исходный ряд условно сходится
Ответ: ряд условно сходится


1>

---

Смотрите также файлы

• Отчет по лабораторной работе 14 По дисциплине.docx

• Задание 1 Сотрудники уголовного розыска должны отказаться от предложения потерпевшего, так как данное предложение можно расценивать, как взятку согласно п. 18 антикорупционного стандарта поведения. Задание 2.docx

• Архаическая культура.doc

• Цель мероприятия.pptx

• Хорошее качество, в полевой форме одежды, можно в полной экипировке.docx