ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 65
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
. Плоскость проходит через ось ОХ и точку М4 (9,-3, 8). Подставляем в это уравнение координаты точки М4 получим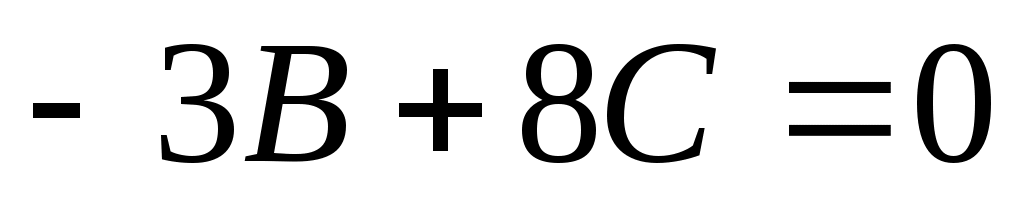 или
или 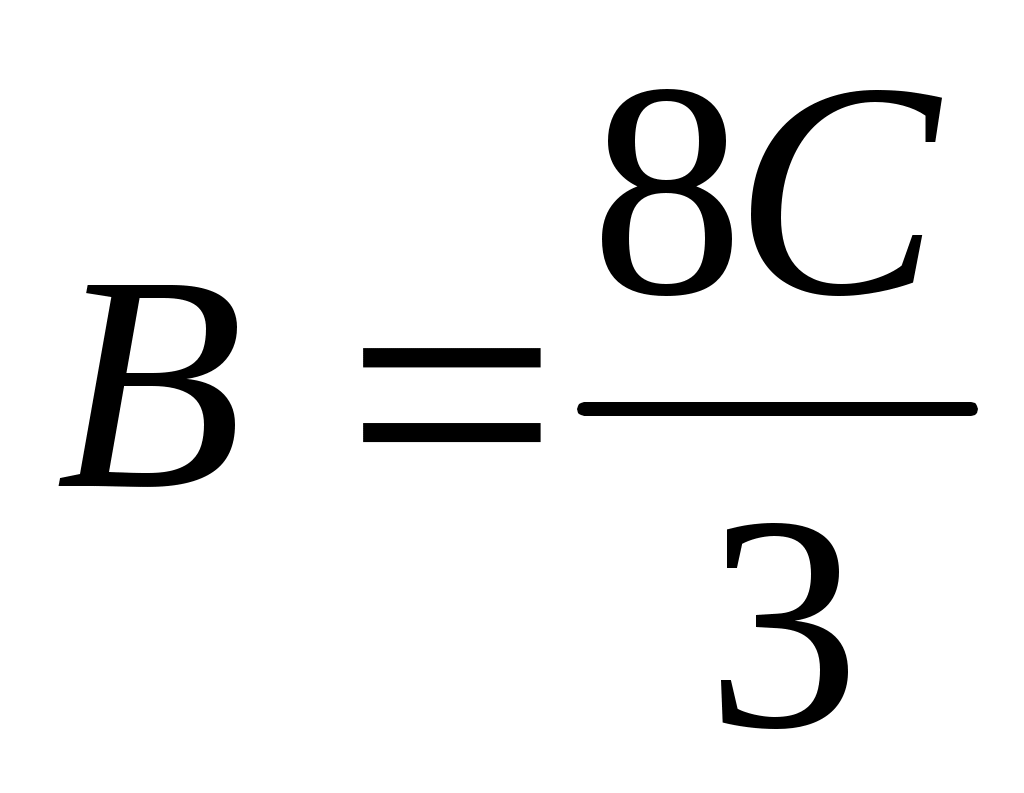 , таким образом, имеем
, таким образом, имеем 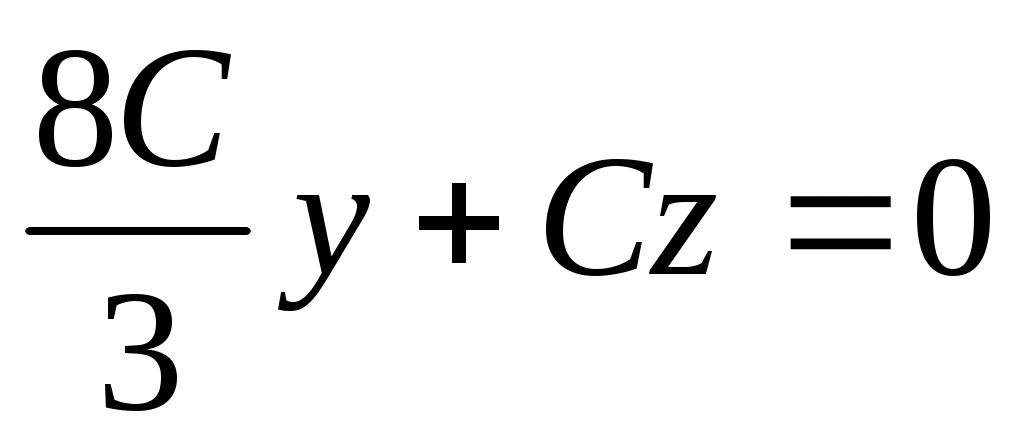 , т. е.
, т. е. 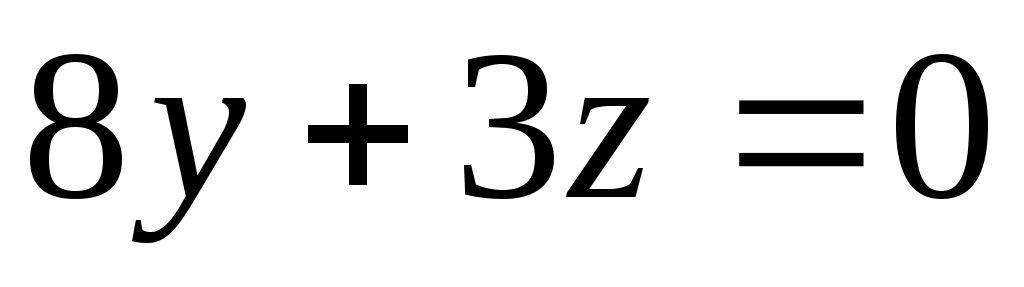 - уравнение плоскости .
- уравнение плоскости .
Угол между плоскостями определяется по формулам , где
, где 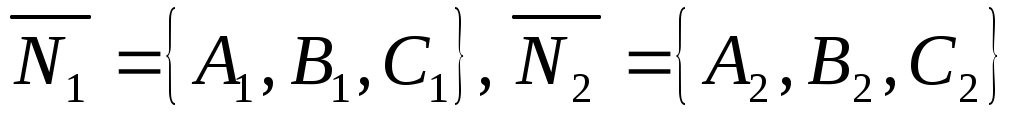 . Нормальный вектор плоскости :
. Нормальный вектор плоскости : 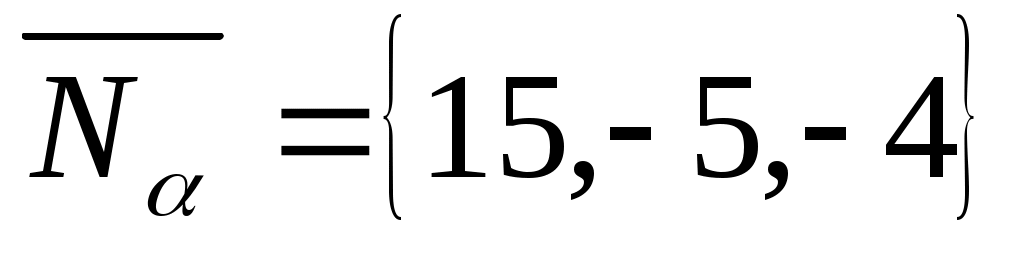 . Для плоскости :
. Для плоскости : 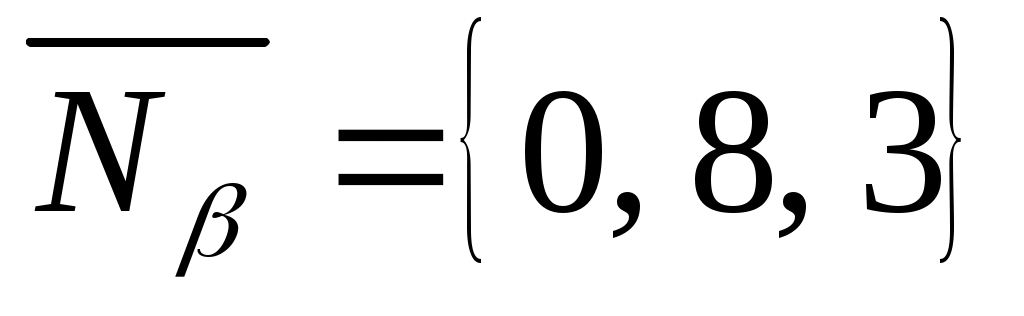 . Определяем острый угол между плоскостями и :
. Определяем острый угол между плоскостями и : 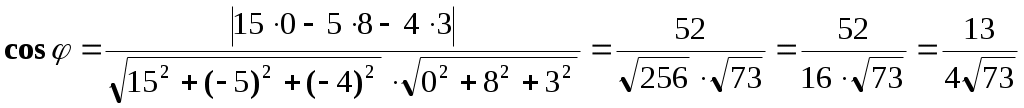
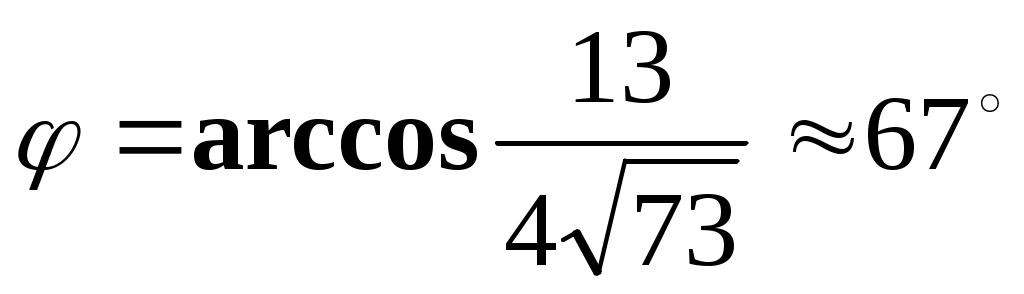 .
.
Решение:
Первый способ. Наметим такой план решения задачи: из системы исключим сначала y и выразим z через x, потом исключим х и выразим z теперь уже через y.
Для того чтобы из системы исключить у, сложим первое уравнение системы почленно со вторым. Получим, что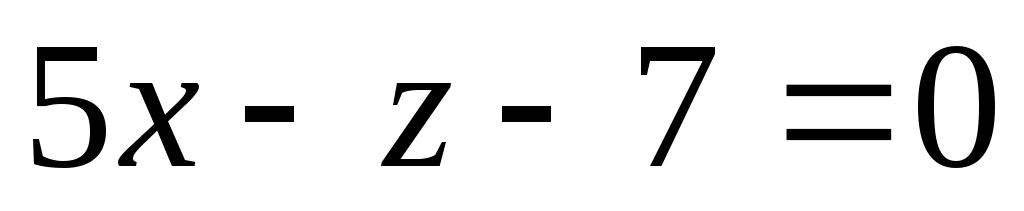 , откуда
, откуда 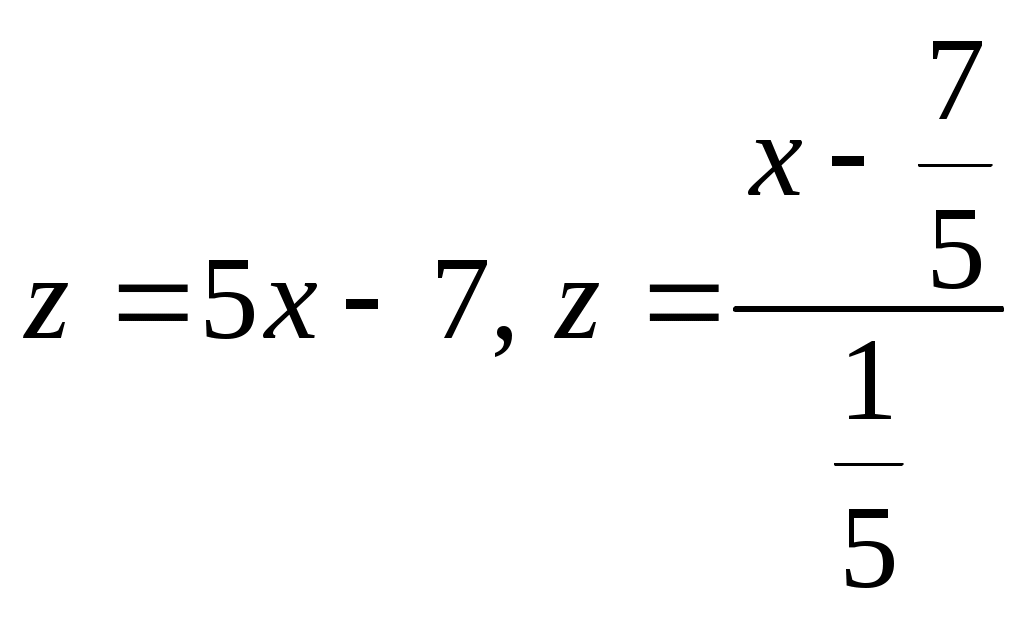 .
.
Умножая первое уравнение на (2), а второе на ,(-3) и складывая их почленно, получим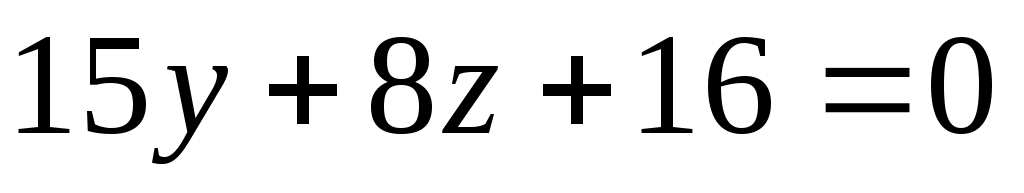 , откуда
, откуда 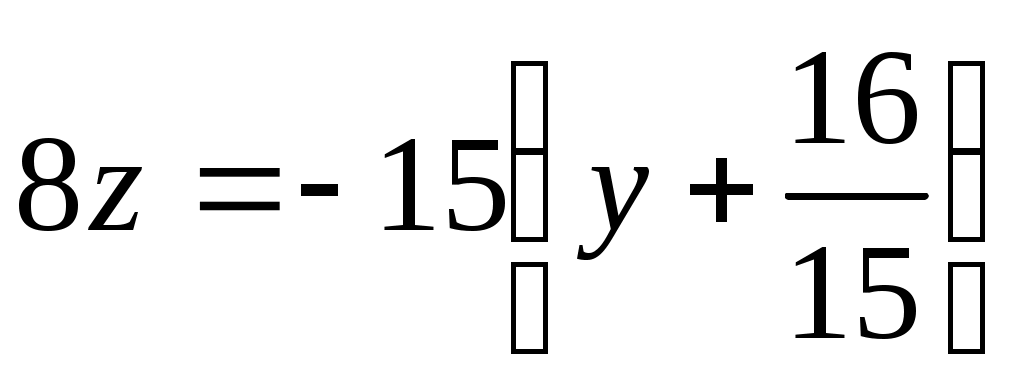 или
или 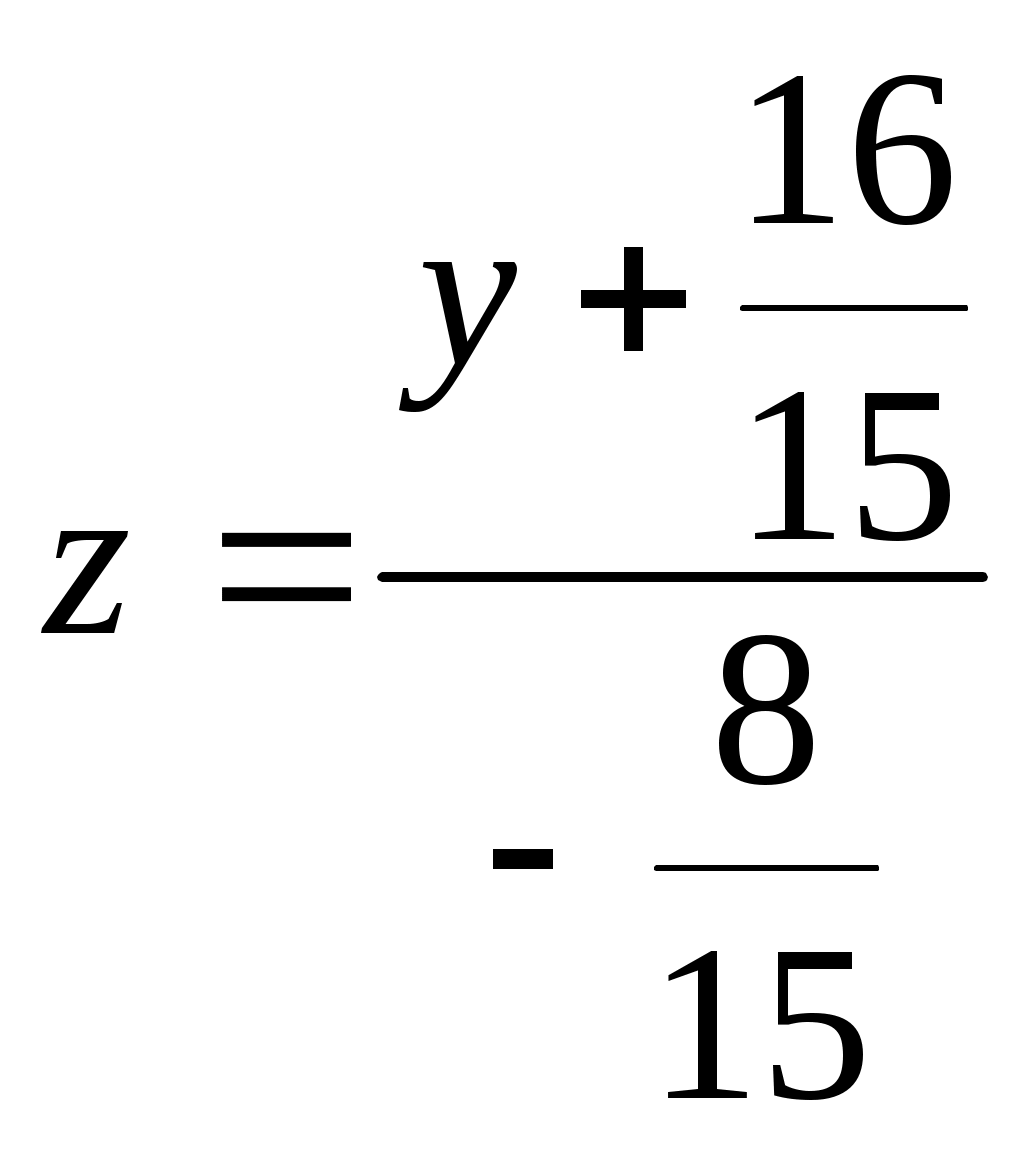 .
.
Сравнивая найденные значения z, получаем уравнение прямой в каноническом виде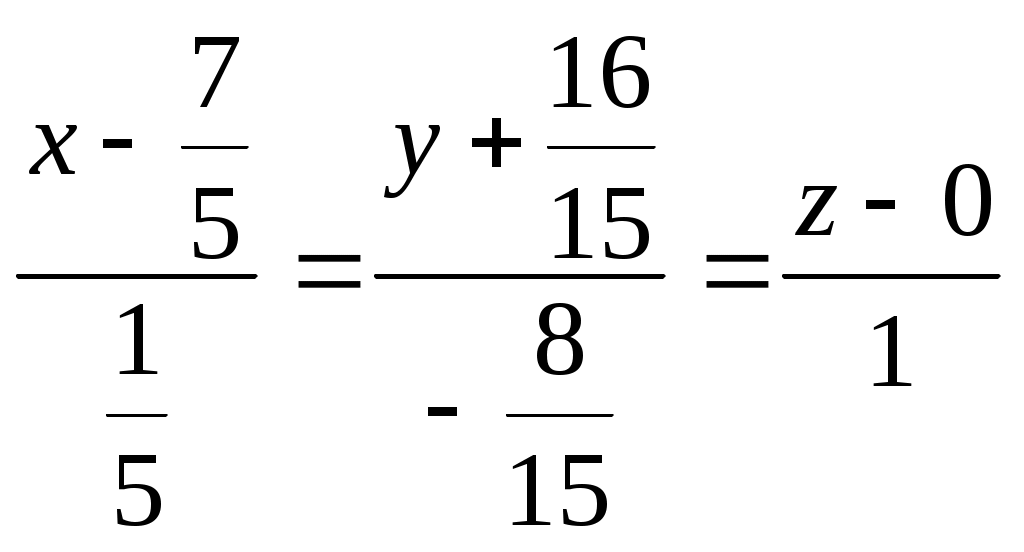 .
.
Умножая теперь все знаменатели на 15, окончательно получим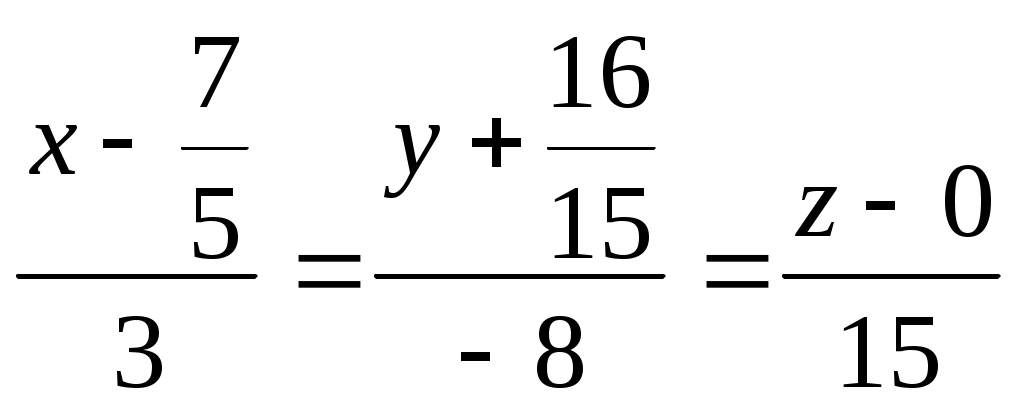
. Прямая проходит через точку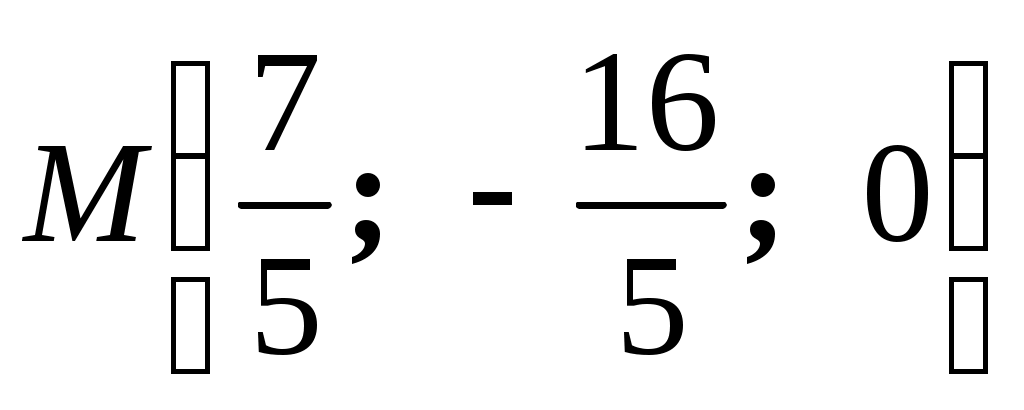 и имеет направляющий вектор
и имеет направляющий вектор 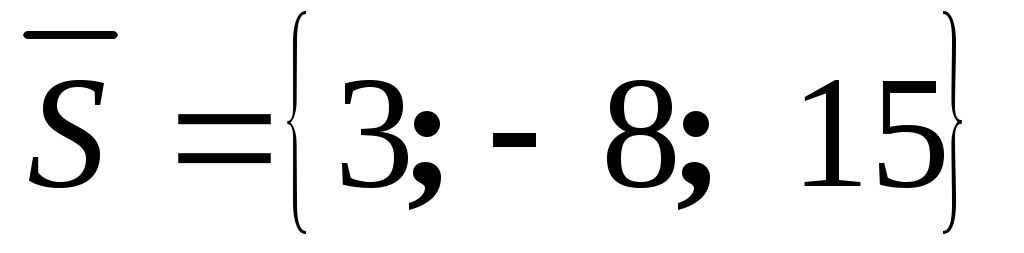 .
.
Второй способ. Найдем направляющий вектор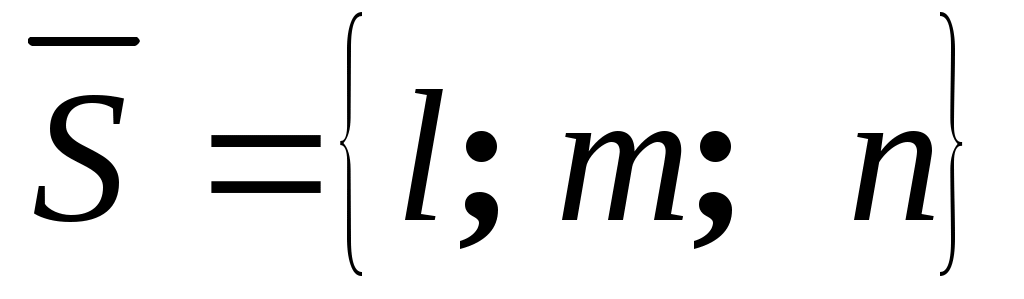 прямой. Так как он должен быть перпендикулярен нормальным векторам заданных плоскостей
прямой. Так как он должен быть перпендикулярен нормальным векторам заданных плоскостей 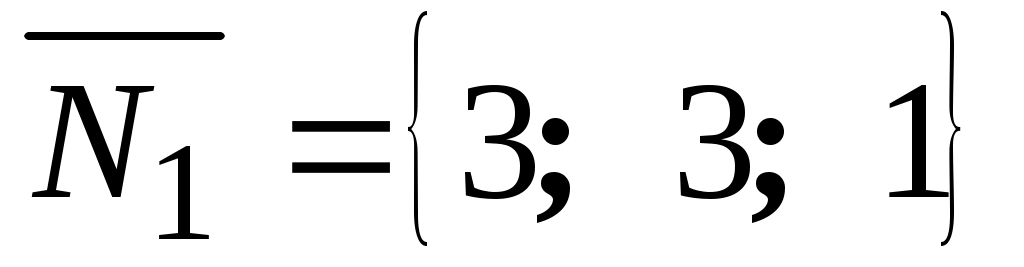 и
и 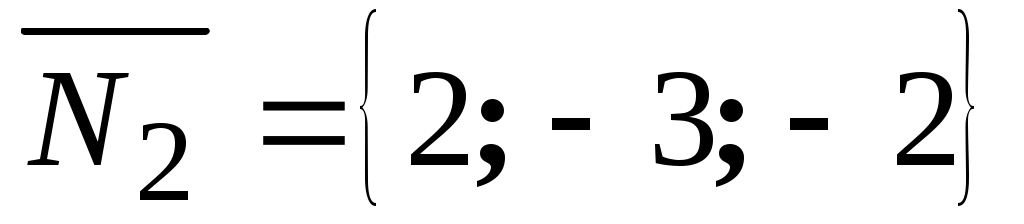 , то в качестве его можно взять векторное произведение векторов
, то в качестве его можно взять векторное произведение векторов 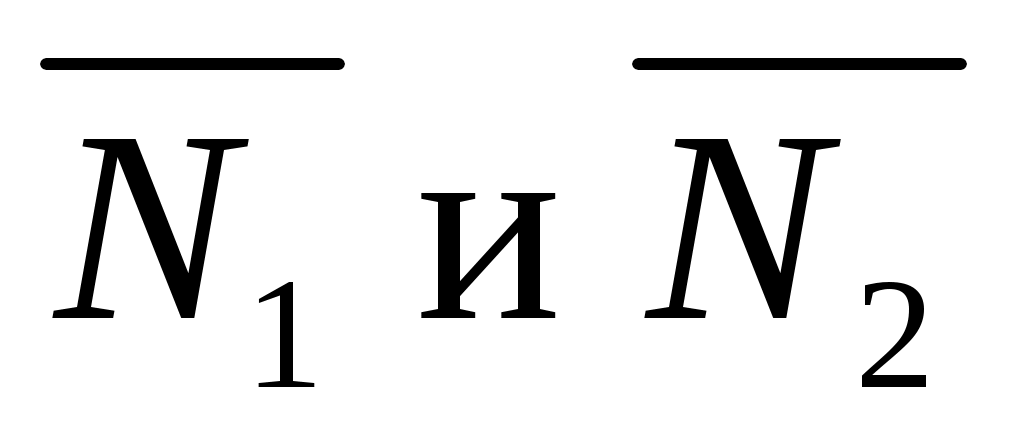 :
: 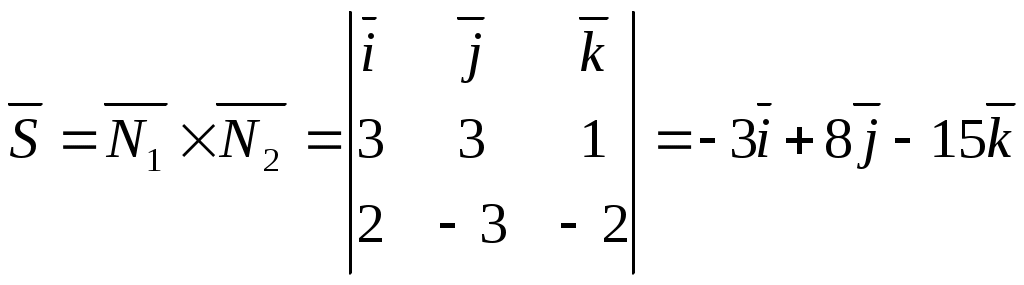 .
.
Таким образом, l = -3, m = 8, n = -15. За точку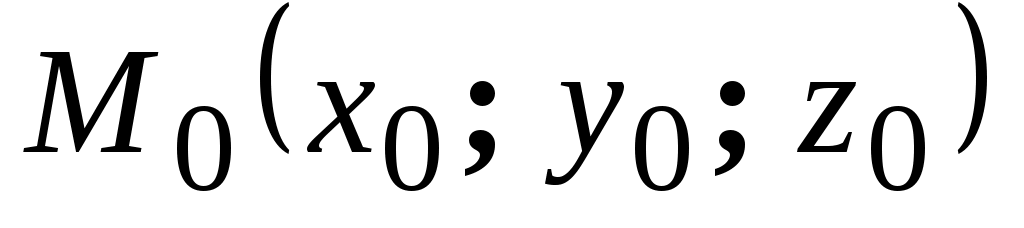 , через которую проходит искомая прямая, можно принять точку её пересечения с любой из координатных плоскостей, например с плоскостью ХOY. Поскольку при этом
, через которую проходит искомая прямая, можно принять точку её пересечения с любой из координатных плоскостей, например с плоскостью ХOY. Поскольку при этом 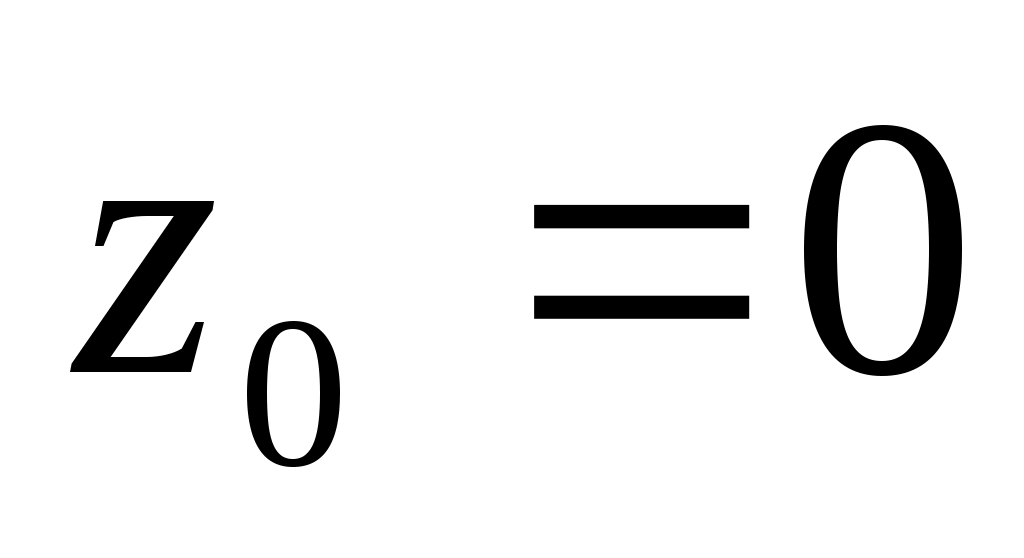 , координаты
, координаты 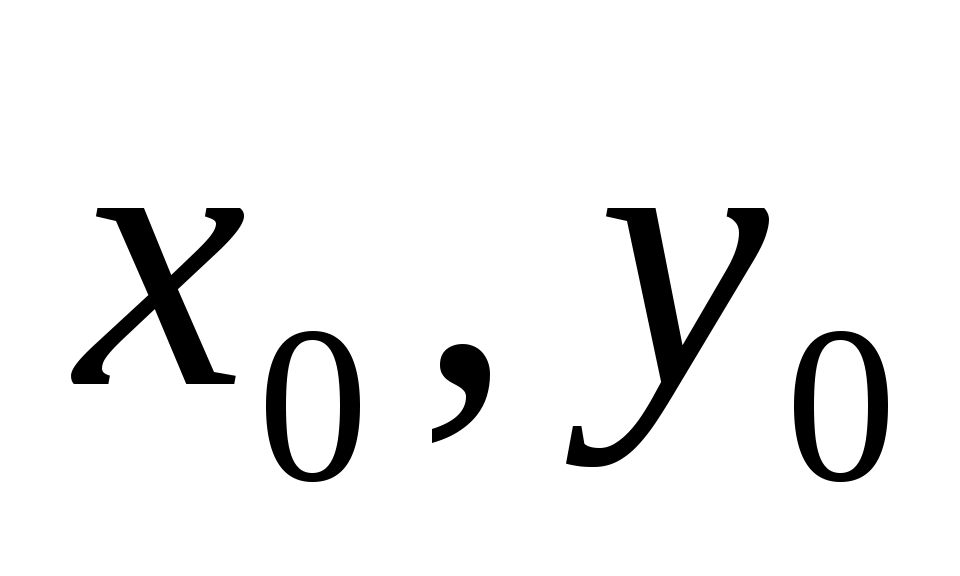 определяются из системы уравнений заданных плоскостей, если положить в них
определяются из системы уравнений заданных плоскостей, если положить в них 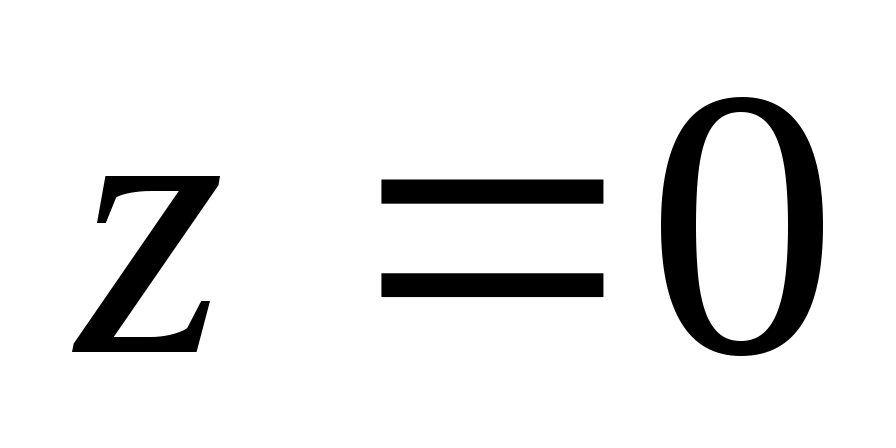
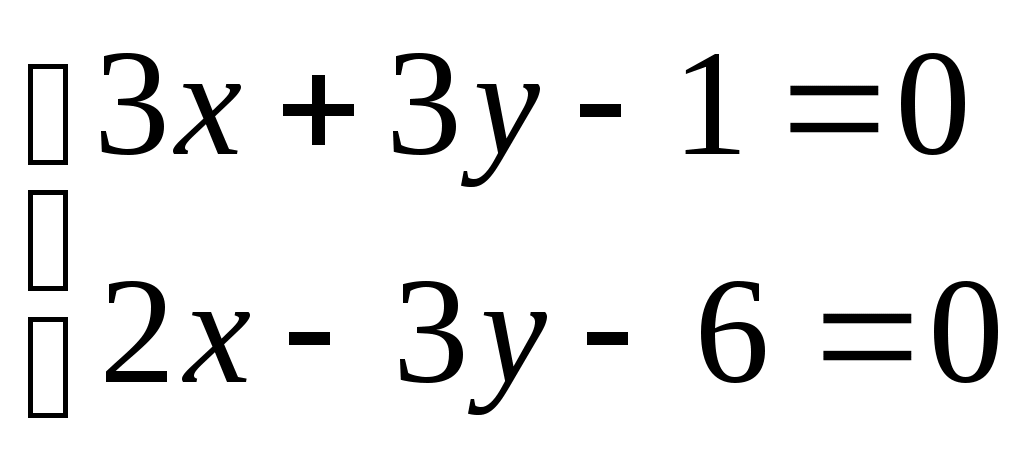 , отсюда получаем
, отсюда получаем 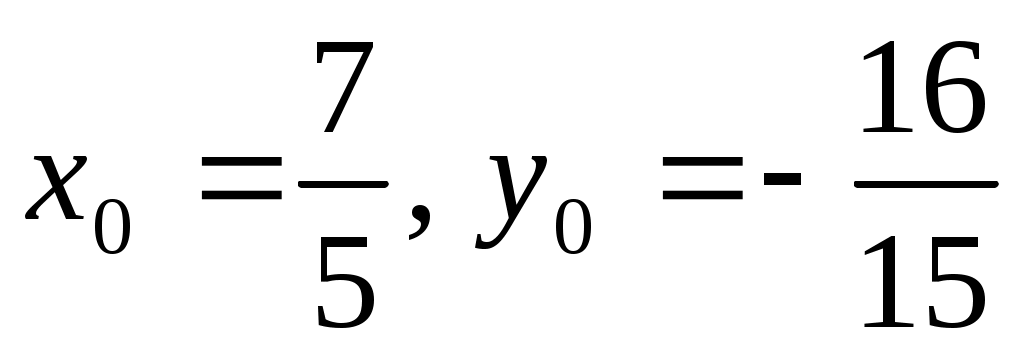 . Так как каноническое уравнение имеет вид
. Так как каноническое уравнение имеет вид 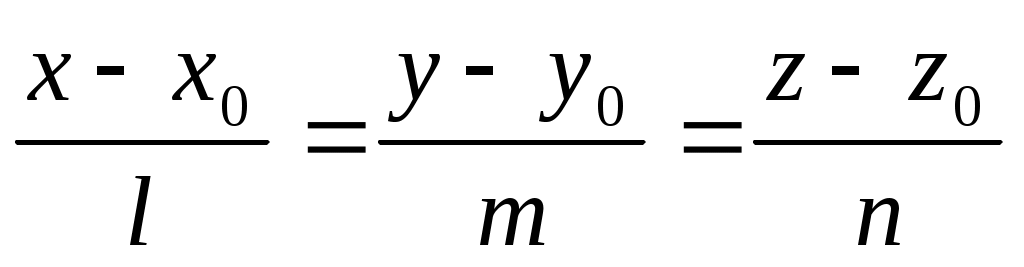 , то в данном случае
, то в данном случае 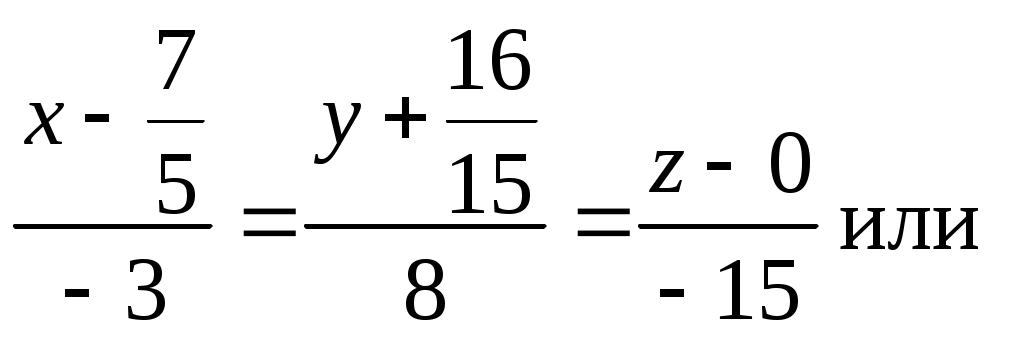
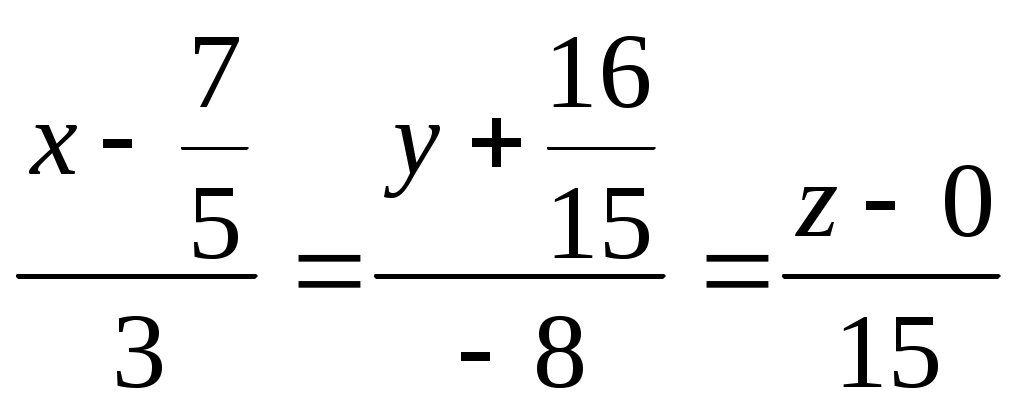 .
.
Решение: Уравнение прямой, проходящей через две данные точки М (х1; y1; z1) и N(x2; y2; z2):
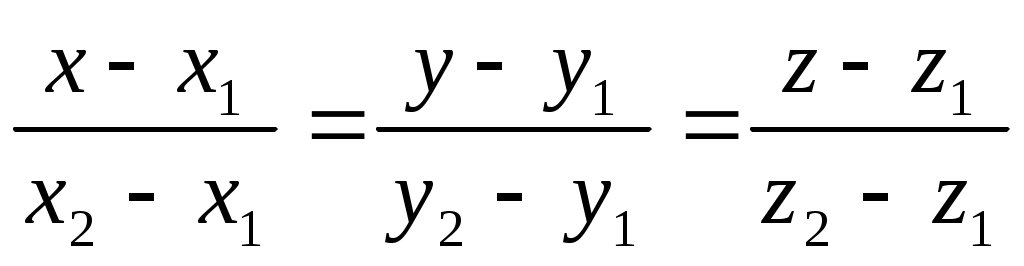
Прямая l: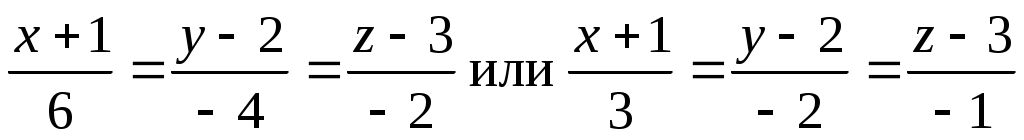 . Подставляем в эти уравнения координаты точек K, L, M, соответственно находим:
. Подставляем в эти уравнения координаты точек K, L, M, соответственно находим: 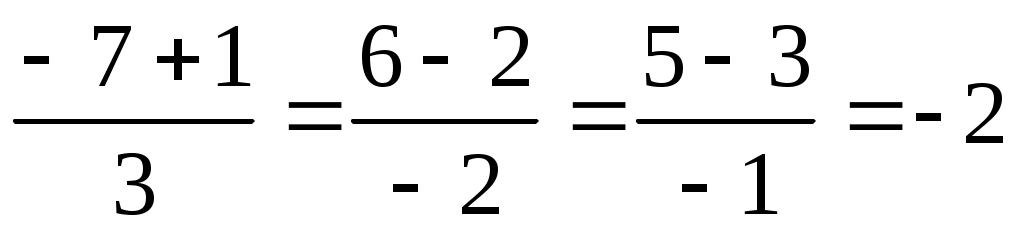 ;
; 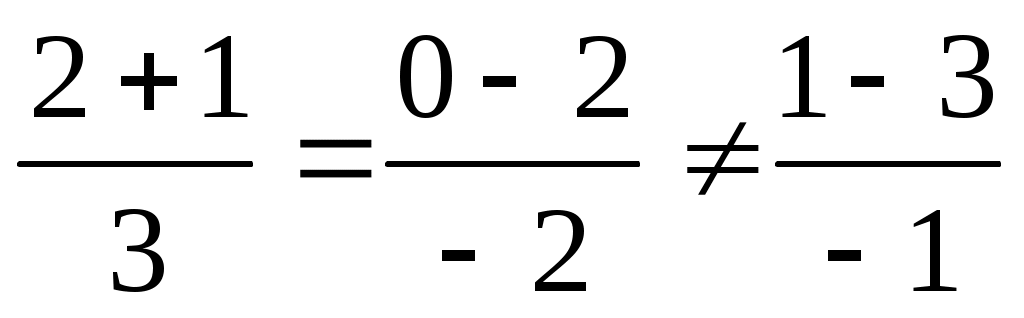 ;
; 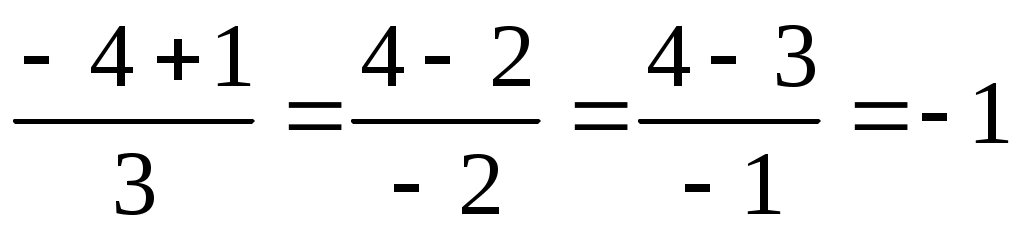 . Следовательно, Kl, Ml, Ll. Условие перпендикулярности двух прямых -
. Следовательно, Kl, Ml, Ll. Условие перпендикулярности двух прямых - 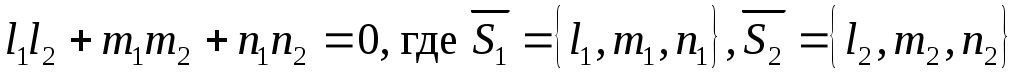 . В данном случае для прямой
. В данном случае для прямой 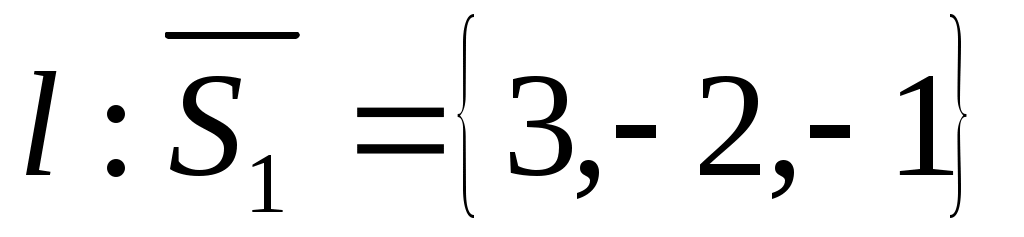
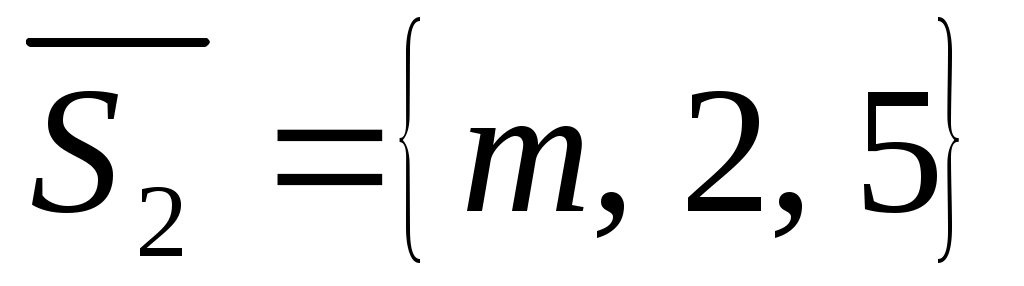 .
.
Тогда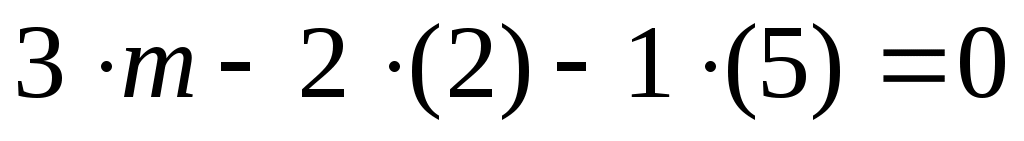
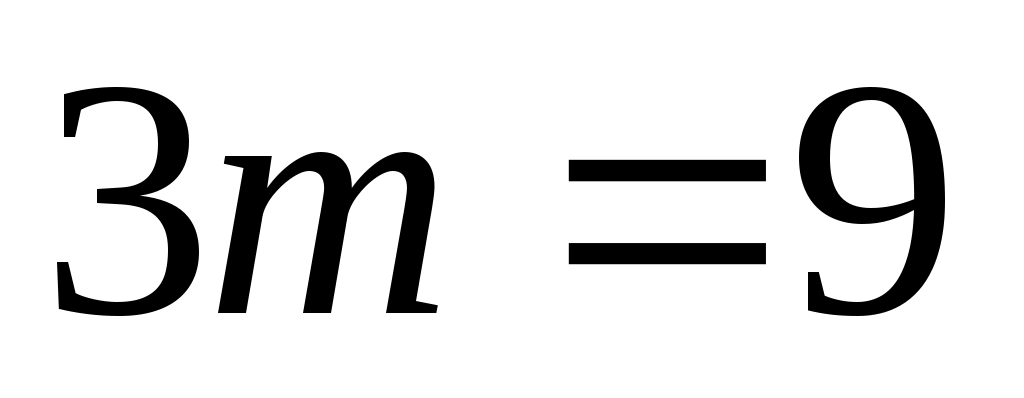
При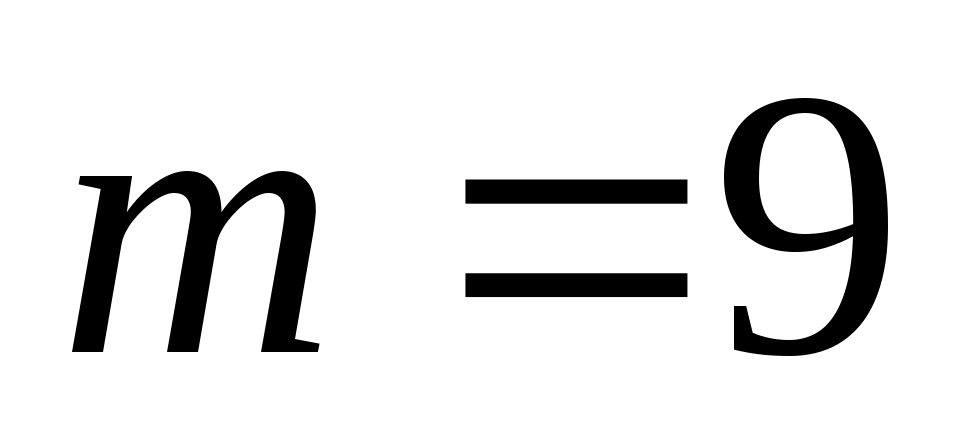 прямые перпендикулярны.
прямые перпендикулярны.
Решение: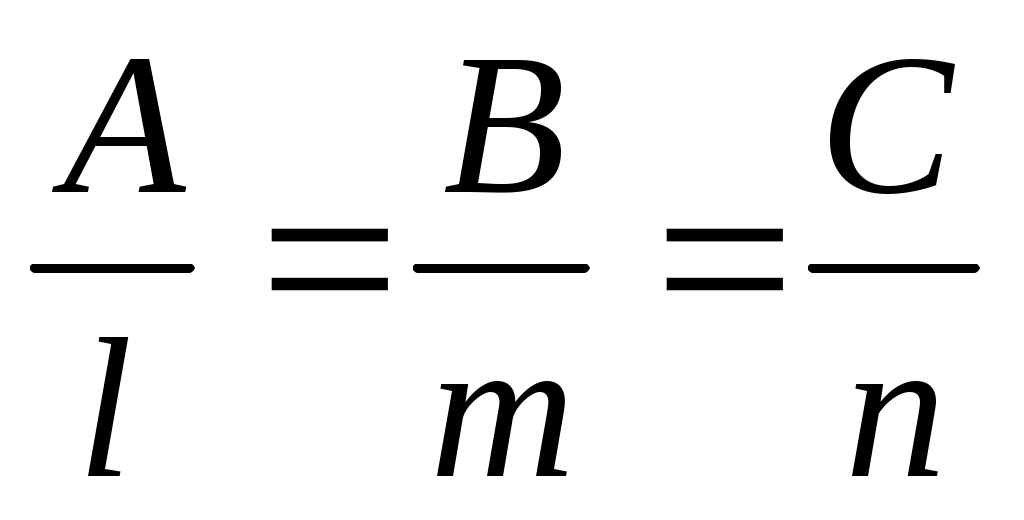 - условие перпендикулярности прямой и плоскости (Рис. 6).
- условие перпендикулярности прямой и плоскости (Рис. 6).
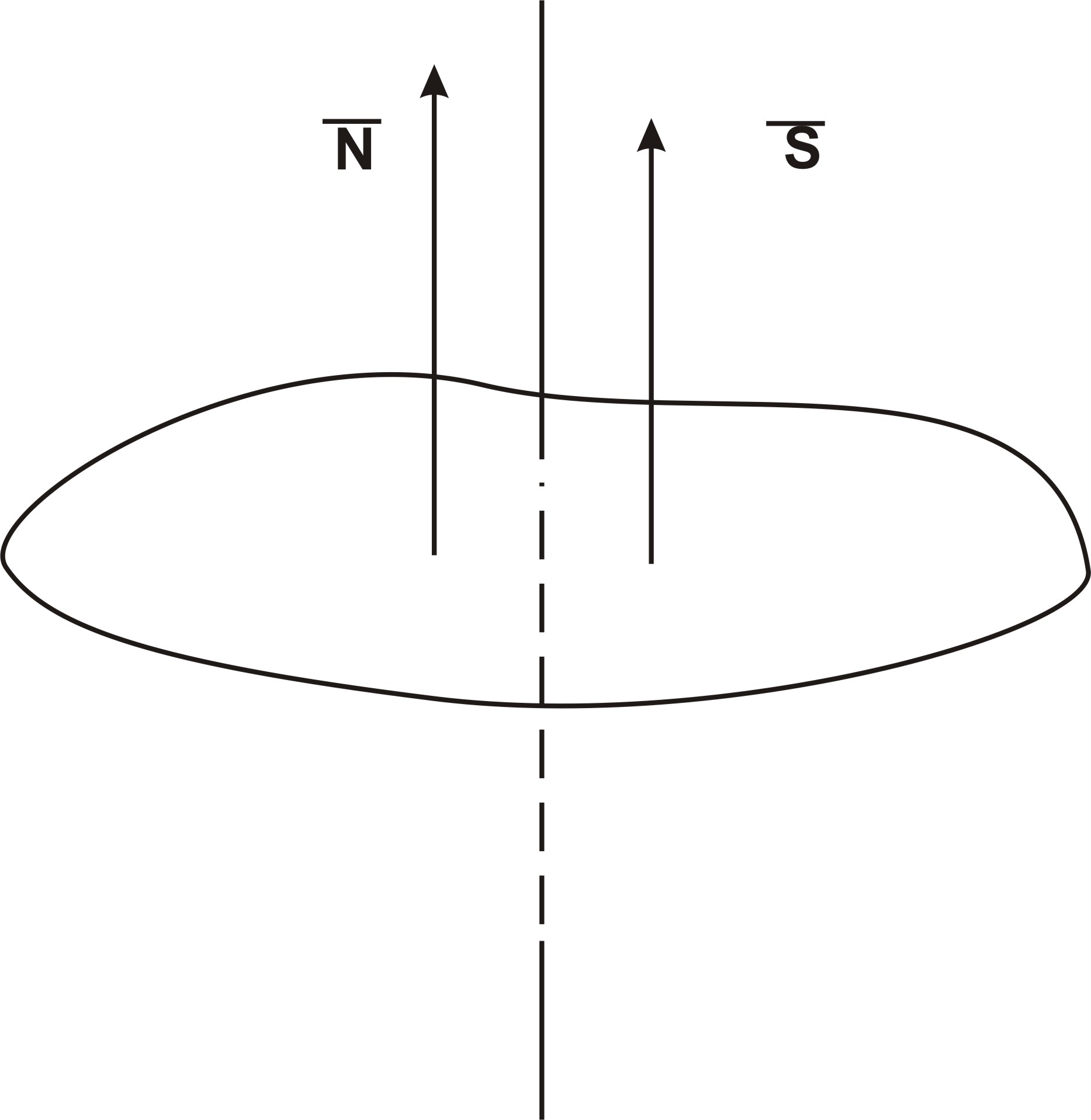
Рис. 6
В данном случае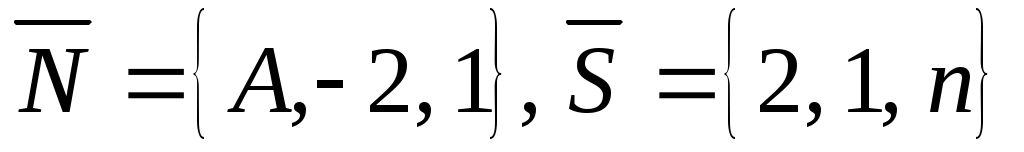
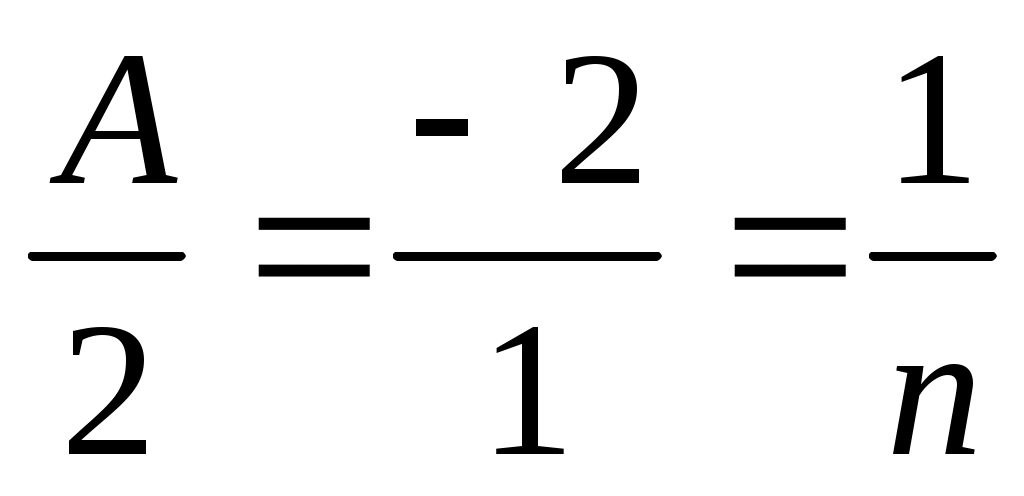
При А = -4; n =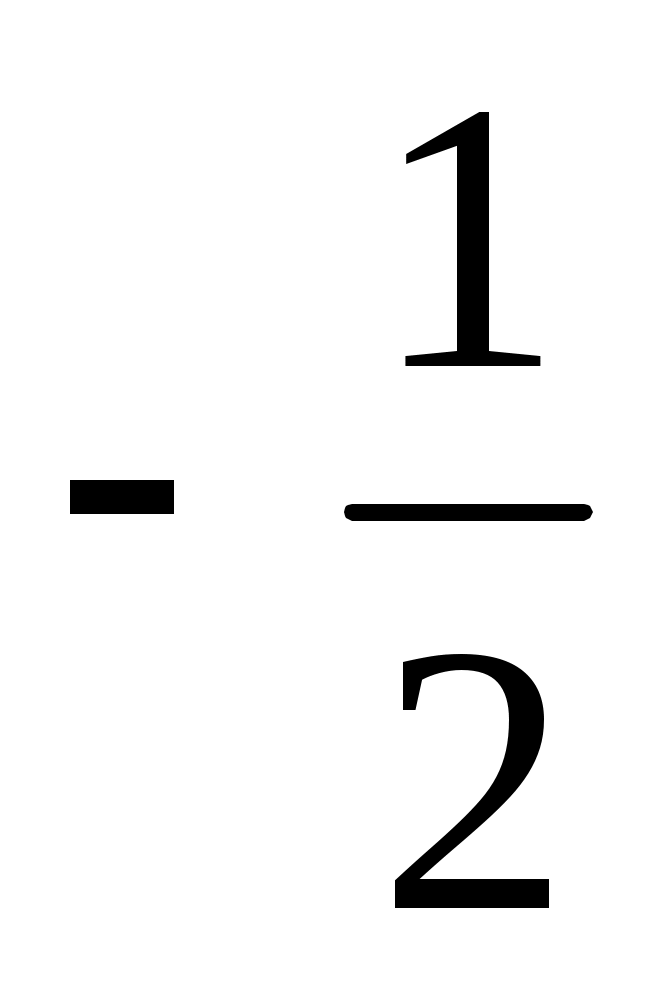 прямая и плоскость перпендикулярны.
прямая и плоскость перпендикулярны.
Если n = -1, то прямая имеет вид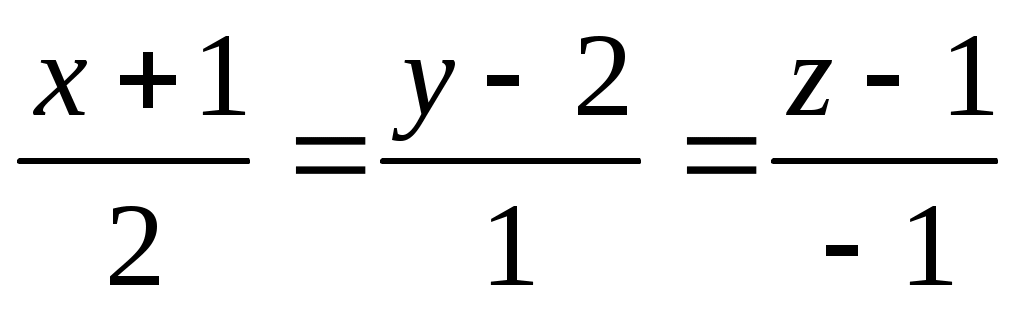 .
.
Если А = 3, то плоскость имеет вид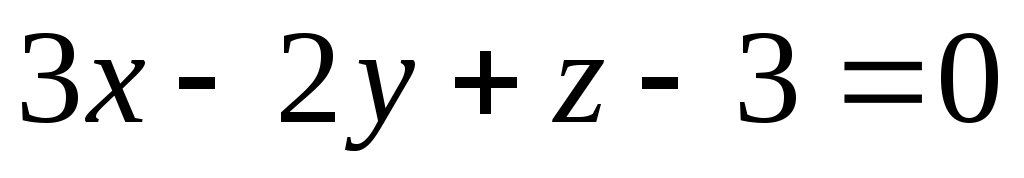 .
.
Запишем уравнение прямой в параметрическом виде: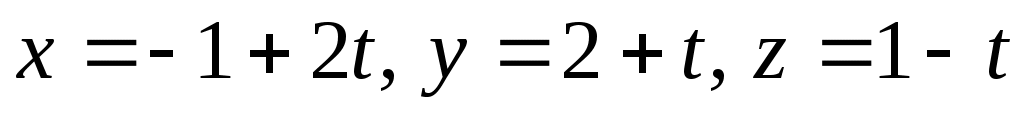 . Подставляя значения x, y, z в уравнение плоскости, имеем
. Подставляя значения x, y, z в уравнение плоскости, имеем
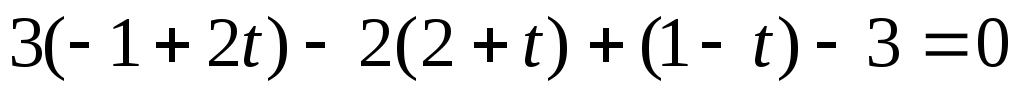 , откуда
, откуда 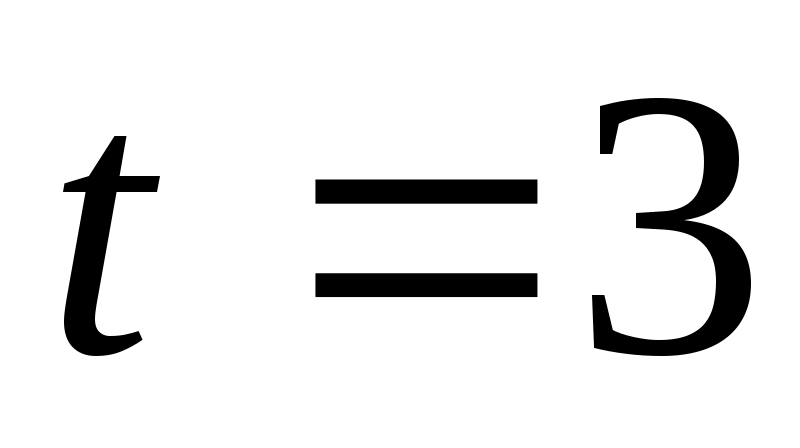 . Подставляя теперь это значение t в параметрические уравнения прямой, находим координаты точки пересечения:
. Подставляя теперь это значение t в параметрические уравнения прямой, находим координаты точки пересечения: 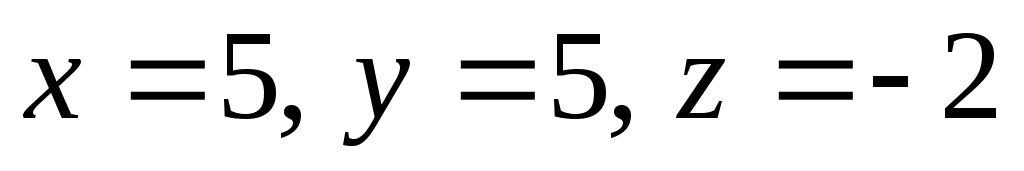 , М (5; 5; -2).
, М (5; 5; -2).
Острый угол между прямой и плоскостью
и плоскостью  определяется по формуле
определяется по формуле 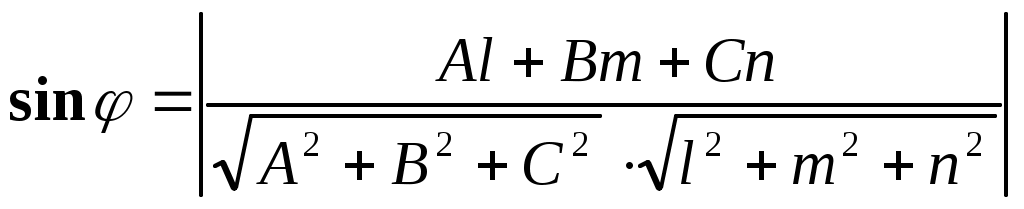 . Учитывая, что
. Учитывая, что 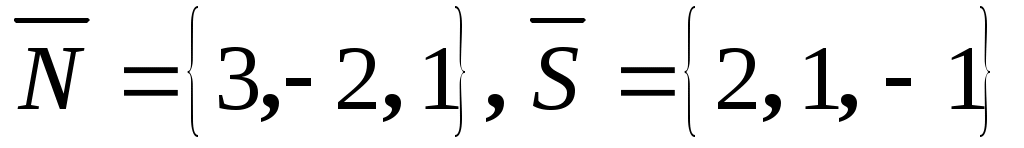 получаем
получаем 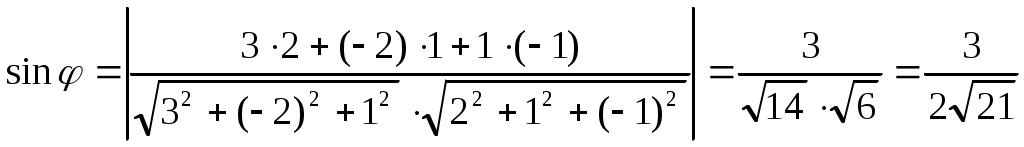

Решение: Проведем через М плоскость , перпендикулярную к данной прямой. :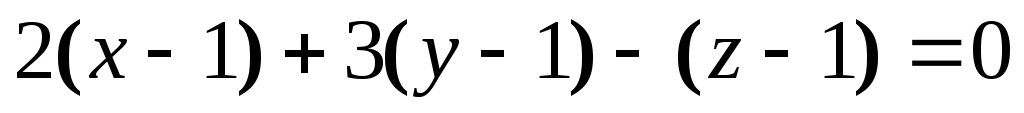 или
или 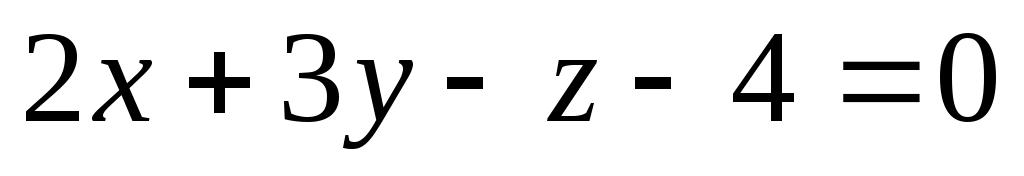 .
.
Найдем точку Q, где эта плоскость пересекает данную прямую. Запишем уравнение прямой в параметрическом виде: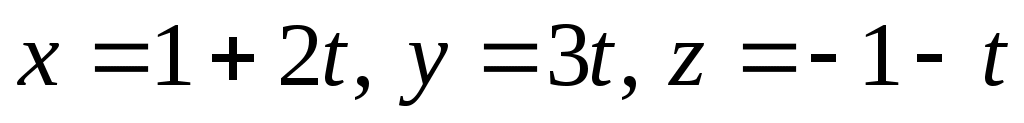 . Подставляя x, y, z в уравнение плоскости, получим
. Подставляя x, y, z в уравнение плоскости, получим 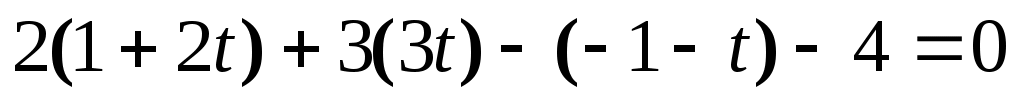 , отсюда
, отсюда 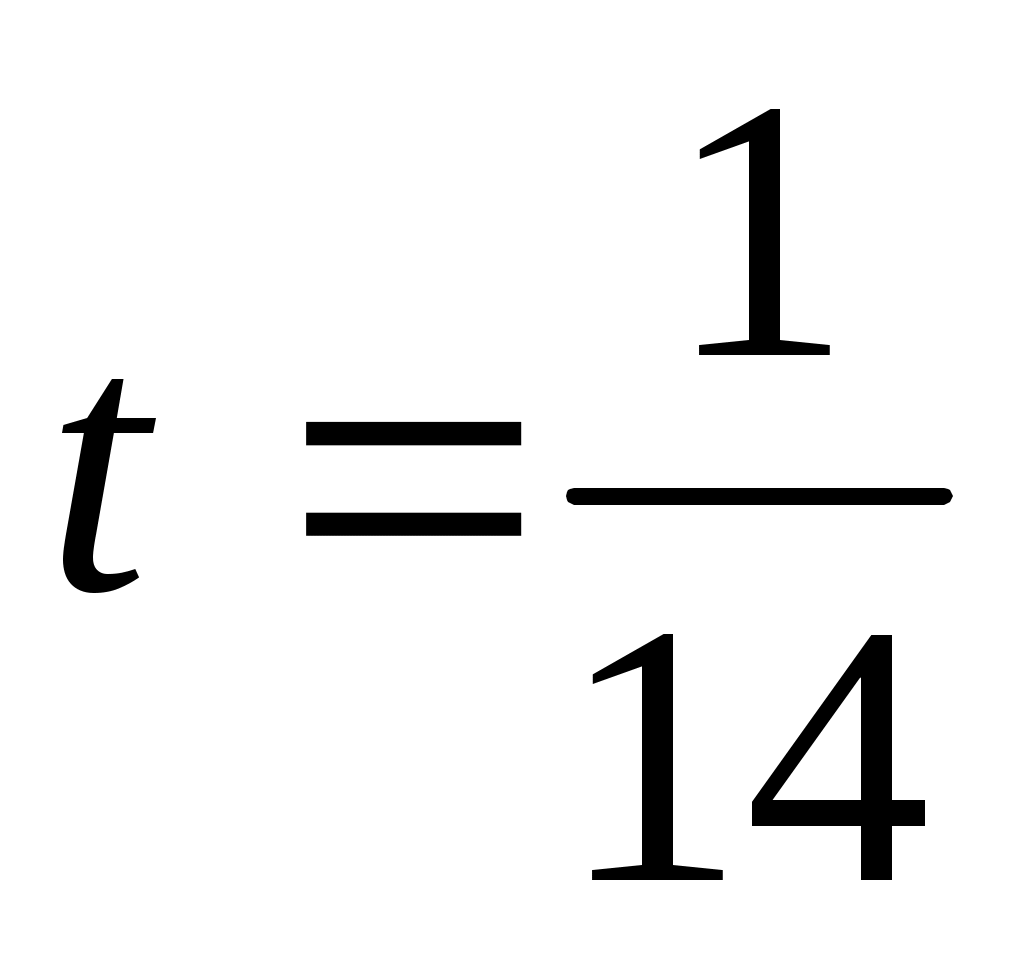
Точка Q имеет координаты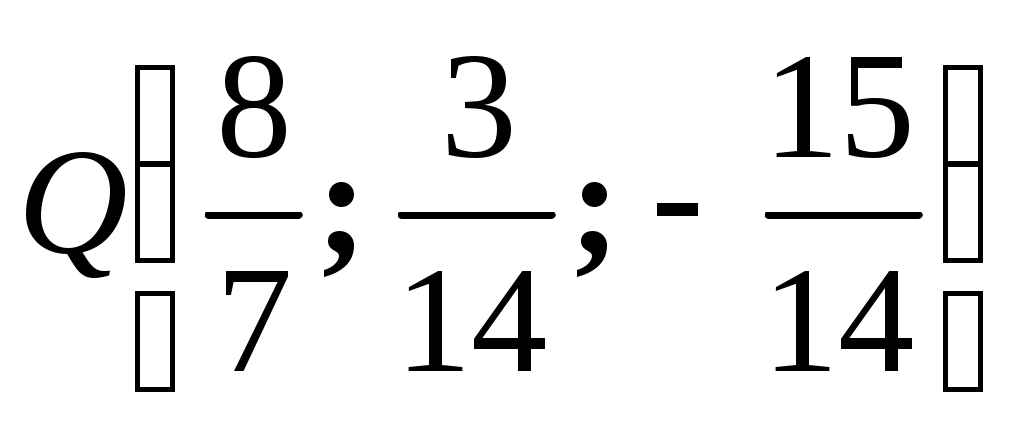 . Тогда координаты симметричной точки можно найти из формулы координат середины отрезка, т. е.
. Тогда координаты симметричной точки можно найти из формулы координат середины отрезка, т. е. 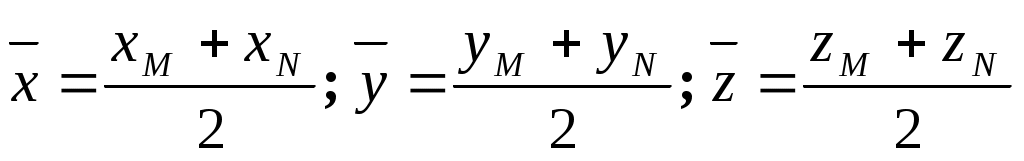 или
или 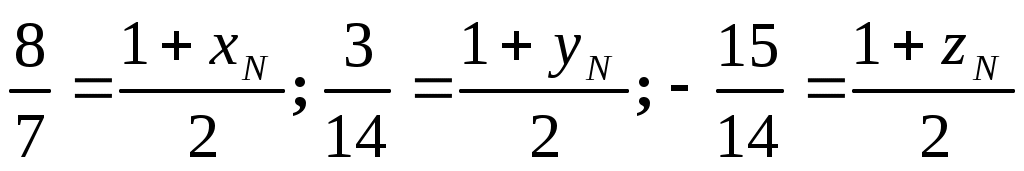 . Откуда
. Откуда 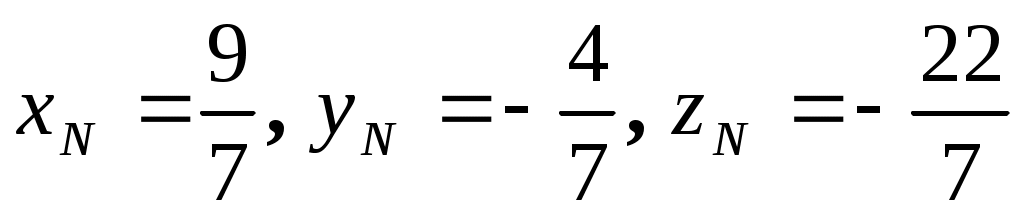 . Следовательно,
. Следовательно, 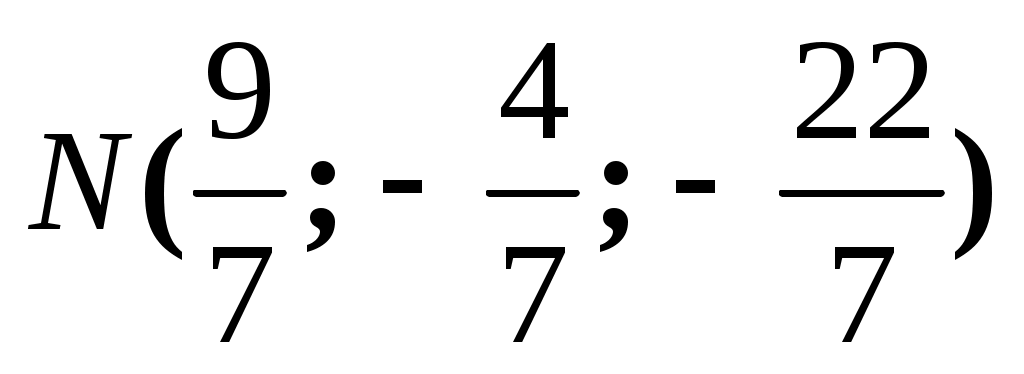
.
Угол между плоскостями определяется по формулам
 , где
, где -
Общее уравнение прямой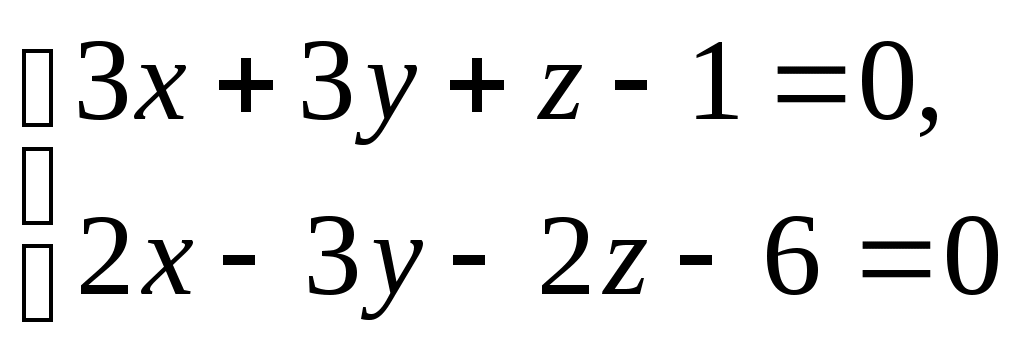 преобразовать к каноническому виду.
преобразовать к каноническому виду.
Решение:
Первый способ. Наметим такой план решения задачи: из системы исключим сначала y и выразим z через x, потом исключим х и выразим z теперь уже через y.
Для того чтобы из системы исключить у, сложим первое уравнение системы почленно со вторым. Получим, что
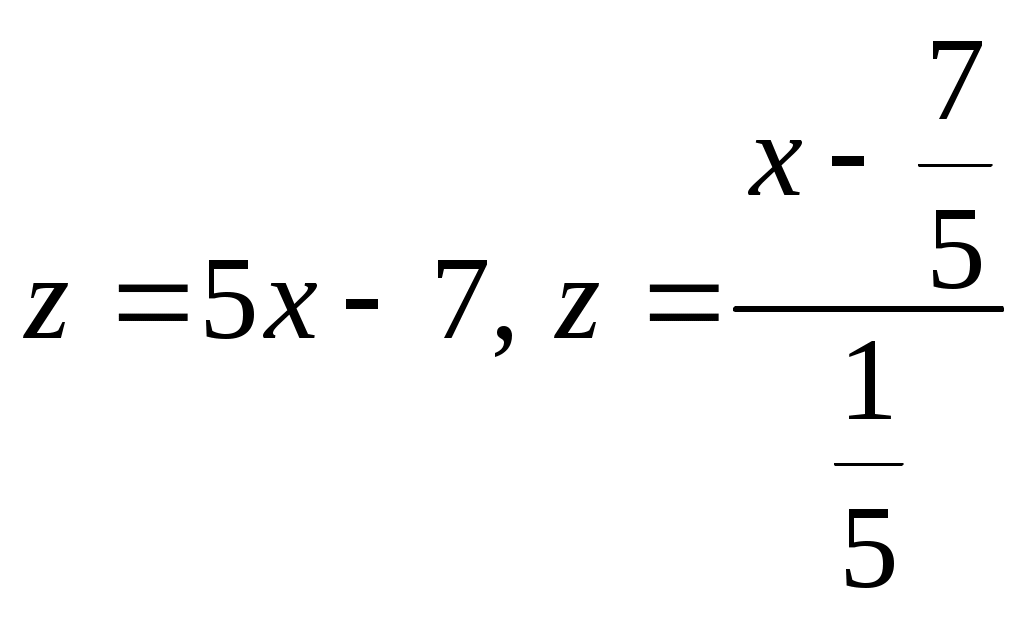 .
.Умножая первое уравнение на (2), а второе на ,(-3) и складывая их почленно, получим
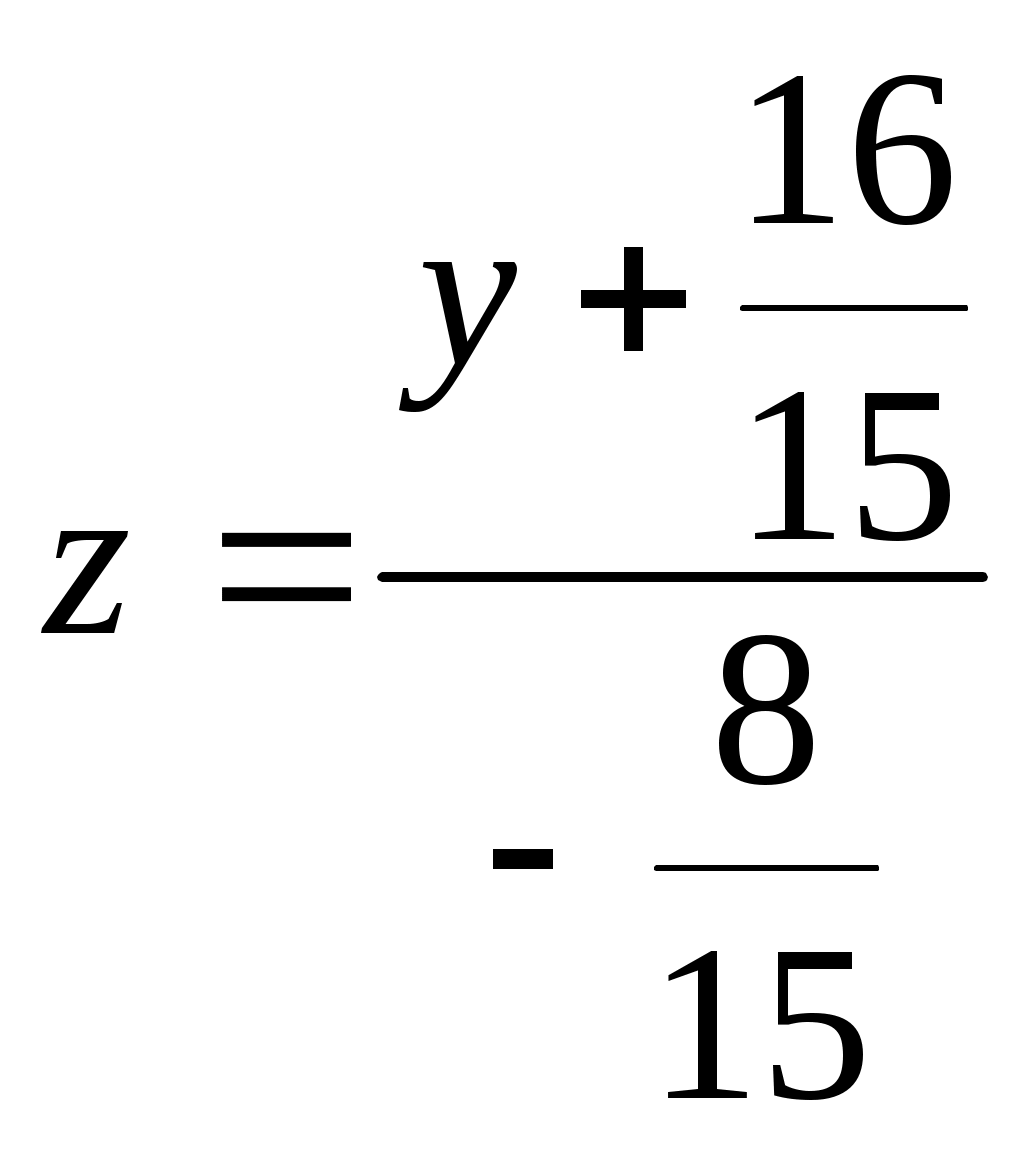 .
.Сравнивая найденные значения z, получаем уравнение прямой в каноническом виде
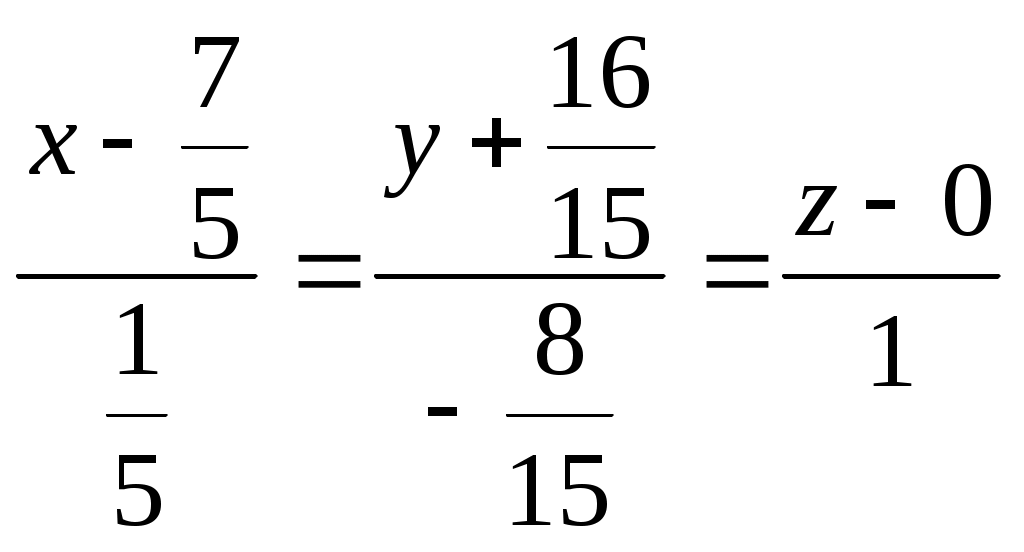 .
.Умножая теперь все знаменатели на 15, окончательно получим
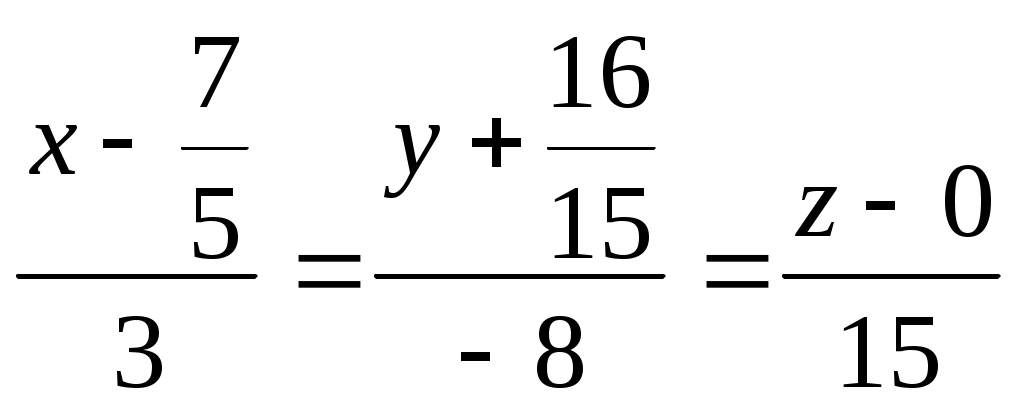
. Прямая проходит через точку
Второй способ. Найдем направляющий вектор
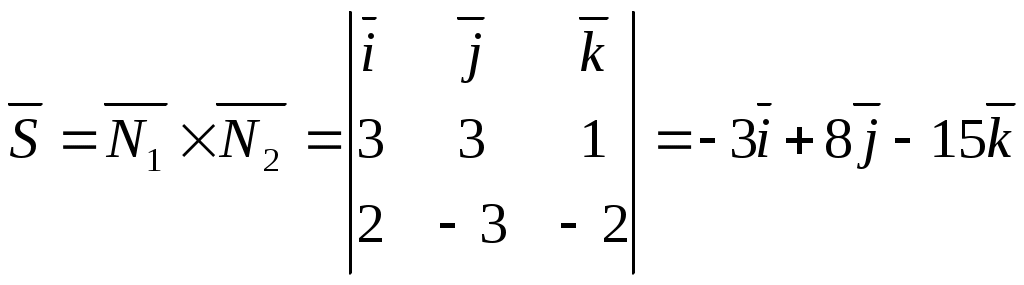 .
. Таким образом, l = -3, m = 8, n = -15. За точку
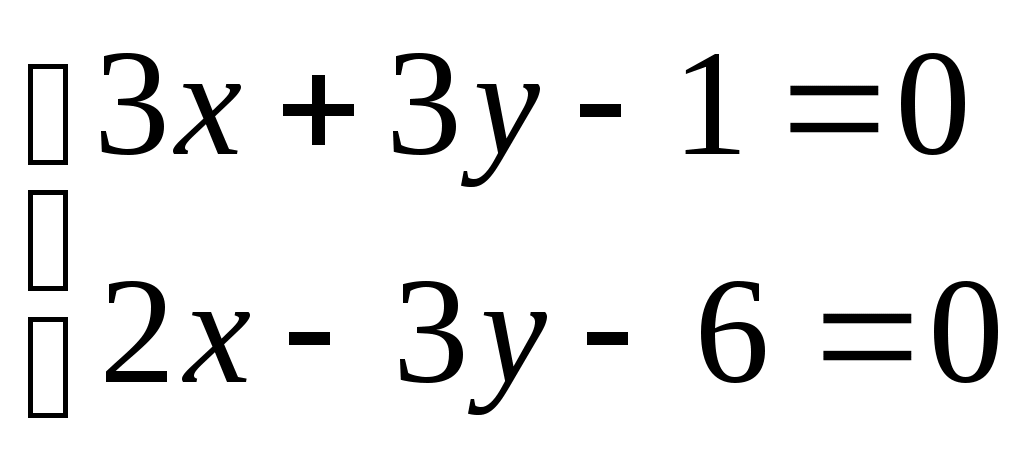 , отсюда получаем
, отсюда получаем 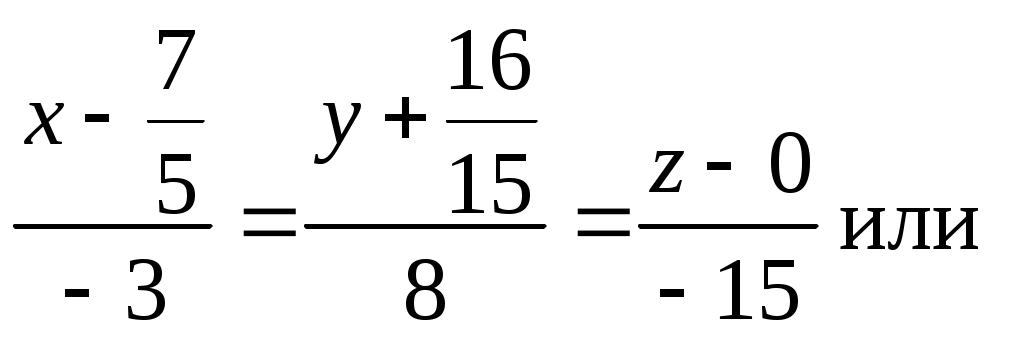
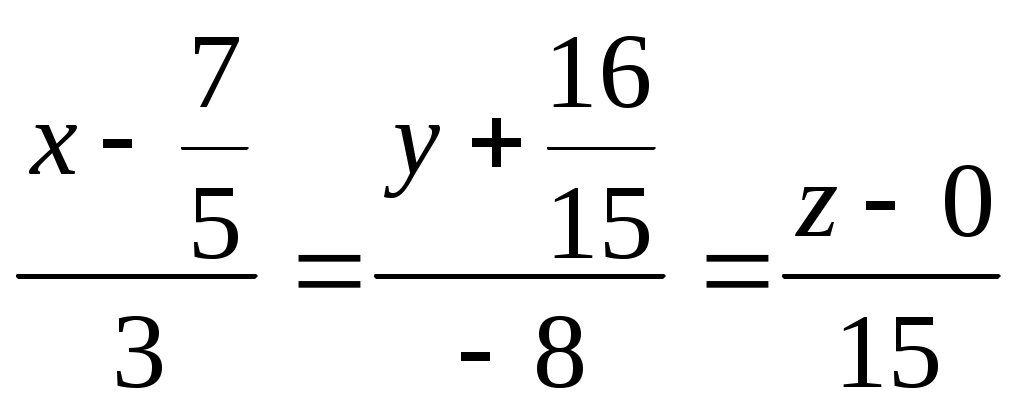 .
.-
Написать уравнение прямой l, проходящей через точки А (-1; 2; 3) и В (5; -2; 1). Лежат ли на этой прямой точки: К (-7; 6; 5), L (2; 0; 1), М (-4; 4; 4)? При каком значении m прямая l перпендикулярна прямой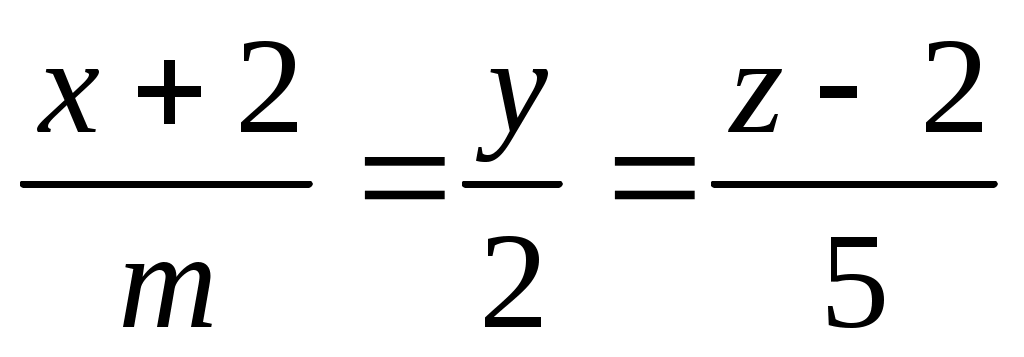 .
.
Решение: Уравнение прямой, проходящей через две данные точки М (х1; y1; z1) и N(x2; y2; z2):
Прямая l:
Тогда
При
-
При каких значениях n и А прямая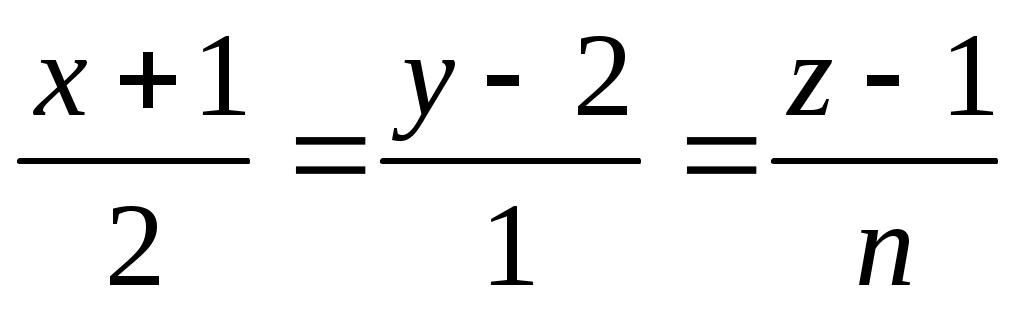 и плоскость
и плоскость 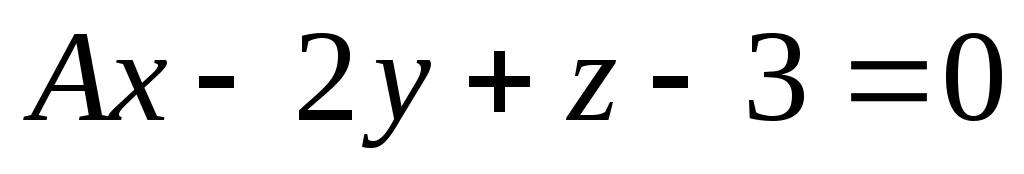 будут перпендикулярны? При n = -1 и А = 3 найти точку пересечения прямой с плоскостью и угол между ними.
будут перпендикулярны? При n = -1 и А = 3 найти точку пересечения прямой с плоскостью и угол между ними.
Решение:

Рис. 6
В данном случае
При А = -4; n =
Если n = -1, то прямая имеет вид
Если А = 3, то плоскость имеет вид
Запишем уравнение прямой в параметрическом виде:
Острый угол между прямой
-
Дана прямая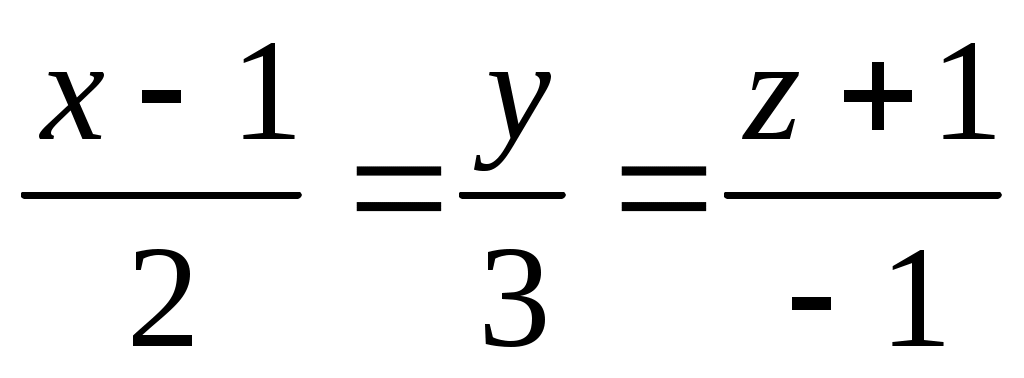 и вне её точка М (1; 1; 1). Найти точку N, симметричную М относительно данной прямой.
и вне её точка М (1; 1; 1). Найти точку N, симметричную М относительно данной прямой.
Решение: Проведем через М плоскость , перпендикулярную к данной прямой. :
Найдем точку Q, где эта плоскость пересекает данную прямую. Запишем уравнение прямой в параметрическом виде:
Точка Q имеет координаты
.