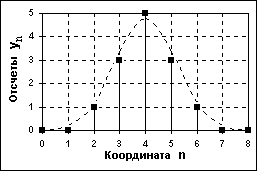
Рис. 1.2.2. Дискретный сигнал Рис. 1.2.3. Цифровой сигнал

y(nt) = 4.8 exp[-(nt-4)2/2.8], t = 1. y_n = Q_k[4.8exp(-(nt-4)2/2.8)], t =1, ,k = 5.

Цифровой сигнал квантован по своим значениям и дискретен по аргументу. Он описывается квантованной решетчатой функцией y_n = Q_k[y(nt)], где Q_k - функция квантования с числом уровней квантования k, при этом интервалы квантования могут быть как с равномерным распределением, так и с неравномерным, например - логарифмическим. Задается цифровой сигнал, как правило, в виде числового массива по последовательным значениям аргумента при t = const, но, в общем случае, сигнал может задаваться и в виде таблицы для произвольных значений аргумента.

По существу, цифровой сигнал является формализованной разновидностью дискретного сигнала при округлении значений последнего до определенного количества цифр, как это показано на рис 1.2.3. В цифровых системах и в ЭВМ сигнал всегда представлен с точностью до определенного количества разрядов, а следовательно всегда является цифровым, С учетом этих факторов при описании цифровых сигналов функция квантования обычно опускается (подразумевается равномерной по умолчанию), а для описания сигналов используются правила описания дискретных сигналов.

В принципе, квантованным по своим значениям может быть и аналоговый сигнал, зарегистрированный соответствующей цифровой аппаратурой (рис. 1.2.4). Но выделять эти сигналы в отдельный тип не имеет смысла - они остаются аналоговыми кусочно-непрерывными сигналами с шагом квантования, который определяется допустимой погрешностью измерений.

Большинство дискретных и цифровых сигналов, с которыми приходится иметь дело, являются аналоговыми по своей природе, дискретизированными в силу методических особенностей измерений или технических особенностей регистрации. Но существуют и сигналы, которые изначально относятся к классу счетных, например гамма-кванты, зарегистрированные по последовательным интервалам времени.



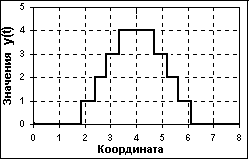
Рис. 1.2.4. Квантованный сигнал y(t) = Q_k[4.8 exp(-(t-4)2/2.8)], k = 5.

Спектральное представление сигналов. Кроме привычного временного (координатного) представления сигналов и функций при анализе и обработке данных широко используется описание сигналов функциями частоты, т.е. по аргументам, обратным аргументам временного (координатного) представления. Возможность такого описания определяется тем, что любой сколь угодно сложный по своей форме сигнал можно представить в виде суммы более простых сигналов, и, в частности, в виде суммы простейших гармонических колебаний, совокупность которых называется частотным спектром сигнала. Математически спектр сигналов описывается функциями значений амплитуд и начальных фаз гармонических колебаний по непрерывному или дискретному аргументу -

---

частоте. Спектр амплитуд обычно называется амплитудно-частотной характеристикой (АЧХ) сигнала, спектр фазовых углов - фазочастотной характеристикой (ФЧХ). Описание частотного спектра отображает сигнал так же однозначно, как и координатное описание.



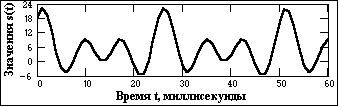
Рис. 1.2.5. Временное представление сигнала.

В качестве примера на рис. 1.2.5 приведен отрезок сигнальной функции, которая получена суммированием постоянной составляющей (частота постоянной составляющей равна 0) и трех гармонических колебаний. Математическое описание сигнала определяется формулой:

s(t) = ,

где A_n = {5, 3, 6, 8} - амплитуда колебаний; f_n = {0, 40, 80, 120} - частота колебаний в герцах; _n = {0, -0.4, -0.6, -0.8} - начальный фазовый угол в радианах, n = 0,1,2,3.

Частотное представление данного сигнала (спектр сигнала в виде АЧХ и ФЧХ) приведено на рис. 1.2.6. Обратим внимание, что частотное представление периодического сигнала s(t), ограниченного по числу гармоник спектра, составляет всего восемь отсчетов и весьма компактно по сравнению с непрерывным временным представлением, определенным в интервале от - до +.



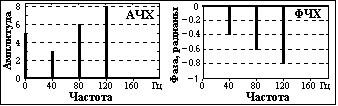
Рис. 1.2.6. Частотное представление сигнала.

Графическое отображение аналоговых сигналов (рис. 1.2.1) особых пояснений не требует. При графическом отображении дискретных и цифровых сигналов используется либо способ непосредственных дискретных отрезков соответствующей масштабной длины над осью аргумента (рис 1.2.6), либо способ огибающей (плавной или ломанной) по значениям отсчетов (пунктирная кривая на рис. 1.2.2). В силу непрерывности полей и, как правило, вторичности цифровых данных, получаемых дискретизацией и квантованием аналоговых сигналов, второй способ графического отображения будем считать основным.

1.3. Модели сигналов

Математическое описание сигналов. Сигналы могут быть объектами теоретических исследований и практического анализа только в том случае, если указан способ их математического описания - математическая модель сигнала.

Слово «модель» произошло от латинского modelium, что означает: мера, способ, образ. Назначение модели состоит в том, что она сохраняет лишь некоторые наиболее важные для исследователя черты объекта-оригинала.

---

Математическое описание позволяет абстрагироваться от физической природы сигнала и материальной формы его носителя, проводить классификацию сигналов, выполнять их сравнение, устанавливать степень тождества или различия, моделировать системы обработки сигналов. Математические модели сигналов позволяют возвращать физическую природу в модель только на заключительном этапе интерпретации данных.

Замечание. В теоретических работах по анализу сигналов конкретные значения величины сигнала (отсчеты значений по аргументу) часто именуют координатами сигнала. Под понятием координат сигнала будем понимать не только какие-либо пространственные координаты, но и любые другие аргументы, на числовой оси которых отложены значения или отсчеты сигнала и рассматривается динамика его изменения.

Математическое описание не может быть всеобъемлющим и идеально точным и, по существу, всегда отображает не реальные объекты, а их упрощенные гомоморфные модели. Как правило, возникает необходимость преодолеть противоречие: простая модель – огрубление свойств объекта; точная модель – учет несущественных свойств.

Модели могут задаваться таблицами, графиками, функциональными зависимостями, уравнениями состояний и переходов из одного состояния в другое и т.п. Формализованное описание может считаться математической моделью оригинала, если оно позволяет с определенной точностью прогнозировать состояние и поведение изучаемых объектов путем формальных процедур над их описанием.

Два вида моделей сигналов. При анализе физических данных используются два основных подхода к созданию математических моделей сигналов.

Первый подход оперирует с детерминированными сигналами, априорно известными или точно предсказуемыми. С математических позиций детерминированный сигнал - это сигнал, который с достаточной степенью точности можно описать явными математическими формулами или вычислительными алгоритмами.

Второй подход предполагает вероятностный (случайный) характер сигналов, которые можно описать только с использованием усредненных (статистических) характеристик. Случайность может быть обусловлена как собственной физической природой сигналов, так и определенным вероятностным характером регистрируемых сигналов как по времени их появления, так и по содержанию.

---

Между этими двумя видами сигналов нет резкой границы. Строго говоря, детерминированных процессов и отвечающих им детерминированных сигналов не существует. Даже сигналы, хорошо известные всегда осложнены случайными помехами, влиянием дестабилизирующих факторов и априорно неизвестными параметрами и строением внешней среды. С другой стороны, модель случайного поля часто аппроксимируется методом суперпозиции (сложения) сигналов известной формы.

На выбор математической модели поля в том или ином случае в немалой степени влияет также сложность математического аппарата обработки сигналов и сложившиеся традиции интерпретации результатов наблюдений. Не исключается и изменение модели, как правило, с переводом из вероятностной в детерминированную, в процессе накопления информации об изучаемом явлении или объекте.

1.3.1. Детерминированные сигналы

Классификация детерминированных сигналов осуществляется на основании существенных признаков соответствующих математических моделей сигналов. Обычно выделяют два класса детерминированных сигналов: периодические и непериодические.

К периодическим относят гармонические и полигармонические сигналы.

Гармонические сигналы(рис. 1.3.1), описываются следующими формулами:

s(t) = Asin(2f₀t+) = Asin(₀t+) или s(t) = Acos(₀t+),

где А, f₀, ₀,  - постоянные величины: А - амплитуда сигнала, f₀ - циклическая частота в герцах, ₀- угловая частота в радианах,  и - начальные фазовые углы в радианах. Период одного колебания T = 1/f₀. При  =  - /2 синусные и косинусные функции описывают один и тот же сигнал. Частотный спектр сигнала представлен амплитудным и фазовым значением одной частоты.



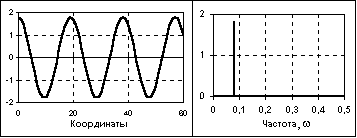
Рис. 1.3.1. Гармонический сигнал и его АЧХ.

Полигармонические сигналы составляют наиболее широко распространенную группу периодических сигналов (рис. 1.3.2) и описываются выражениями:

s(t) =

---

,

или: s(t) = y(t  kT_p), k = 1,2,3,..., где Т_p - период одного полного колебания сигнала. Число циклов колебаний за единицу независимой переменной t называют фундаментальной частотой f_p = 1/T_p. Полигармонические сигналы представляют собой сумму определенной постоянной составляющей и произвольного (в пределе - бесконечного) числа гармонических составляющих с частотами, кратными фундаментальной частоте f_p, и с произвольными значениями амплитуд A_nи фаз _n. Другими словами, частотный спектр полигармонических сигналов дискретен, поэтому получило широкое распространение математическое представление сигналов - в виде спектров (рядов Фурье).



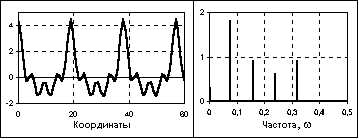
Рис. 1.3.2. Полигармонический сигнал и его АЧХ.

К непериодическим сигналам относят почти периодические и апериодические или переходные сигналы.

Почти периодические сигналы близки по своей форме к полигармоническим (pис. 1.3.3). Они также представляют собой сумму двух и более гармонических сигналов, но не с кратными, а с произвольными частотами, отношения которых (хотя бы двух частот минимум) не относятся к рациональным числам, вследствие чего фундаментальный период суммарных колебаний бесконечно велик. Как правило, почти периодические сигналы порождаются физическими процессами, не связанными между собой.

s(t) = .

Частотный спектр почти периодических сигналов также дискретен.



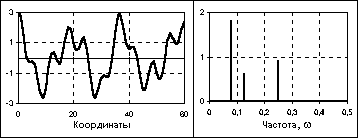
Рис. 1.3.3. Почти периодический сигнал и его АЧХ.

Апериодические сигналы составляют основную группу непериодических сигналов и задаются произвольными функциями времени. На рис. 1.3.4 показан пример апериодического сигнала, заданного формулой на интервале (0, ):

s(t) = exp(-0.15t) - exp(-0.17t).

Частотный спектр апериодических сигналов непрерывен и для их представления в частотной области используется интегральное преобразование Фурье.



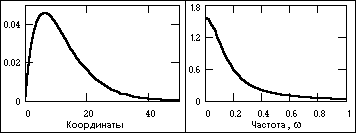
Рис. 1.3.4. Апериодический сигнал и модуль его спектра.

К апериодическим сигналам относятся также и

---

Смотрите также файлы

• Совершенствование техники чтения.ppt

• Лекция 15. Преобразователи кодов, шифраторы и дешифраторы Преобразователи кодов. Операция изменения кода числа называется его перекодированием..docx

• Влияние физической и социальной окружающей среды на межкультурное взаимодействие.doc

• Конкурса Бухгалтерпрофессионал 2019.doc

• Наименование разделов и тем Планируемые результаты.doc