Файл: Обработка сигналов введение в теорию сигналов введение в теорию сигналов общие сведения и понятия Понятие сигнала.doc
Добавлен: 10.01.2024
Просмотров: 85
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
импульсные сигналы. Импульсы представляют собой сигналы достаточно простой формы (рис. 1.3.5), существующие в пределах конечных временных интервалов.
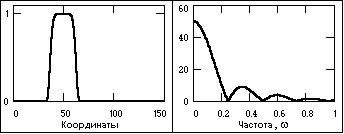
Рис. 1.3.5. Импульсный сигнал и модуль его спектра.
В классе импульсных сигналов выделяют подкласс радиоимпульсов. Пример радиоимпульса приведен на рис. 1.3.6. Уравнение радиоимпульса имеет вид
s(t) = u(t) cos(2f0 t+0).
где cos(2f0t+0) - гармоническое колебание заполнения радиоимпульса, u(t) – огибающая радиоимпульса или видеоимпульс.
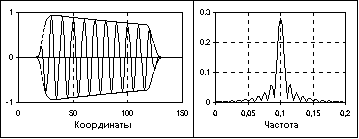
Рис. 1.3.6. Радиоимпульс и модуль его спектра.
1.3.2. Классификация случайных сигналов
Случайный сигнал отображает случайное физическое явление или физический процесс. Зарегистрированный в единичном наблюдении сигнал не воспроизводится с достаточной математической точностью при повторных наблюдениях и не может быть описан явной математической зависимостью. При регистрации случайного сигнала реализуется только один из возможных вариантов (исходов) случайного процесса, а достаточно полное и точное описание процесса в целом можно произвести только после многократного повторения наблюдений и вычисления определенных статистических характеристик ансамбля реализаций сигнала.
Случайные сигналы подразделяют на стационарные и нестационарные. Стационарные случайные сигналы сохраняют свои статистические характеристики в последовательных реализациях случайного процесса. Что касается нестационарных случайных сигналов, то их общепринятой классификации не существует. Как правило, из них выделяют различные группы сигналов по особенностям их нестационарности.

Рис. 1.3.5. Импульсный сигнал и модуль его спектра.
В классе импульсных сигналов выделяют подкласс радиоимпульсов. Пример радиоимпульса приведен на рис. 1.3.6. Уравнение радиоимпульса имеет вид
s(t) = u(t) cos(2f0 t+0).
где cos(2f0t+0) - гармоническое колебание заполнения радиоимпульса, u(t) – огибающая радиоимпульса или видеоимпульс.

Рис. 1.3.6. Радиоимпульс и модуль его спектра.
1.3.2. Классификация случайных сигналов
Случайный сигнал отображает случайное физическое явление или физический процесс. Зарегистрированный в единичном наблюдении сигнал не воспроизводится с достаточной математической точностью при повторных наблюдениях и не может быть описан явной математической зависимостью. При регистрации случайного сигнала реализуется только один из возможных вариантов (исходов) случайного процесса, а достаточно полное и точное описание процесса в целом можно произвести только после многократного повторения наблюдений и вычисления определенных статистических характеристик ансамбля реализаций сигнала.
Случайные сигналы подразделяют на стационарные и нестационарные. Стационарные случайные сигналы сохраняют свои статистические характеристики в последовательных реализациях случайного процесса. Что касается нестационарных случайных сигналов, то их общепринятой классификации не существует. Как правило, из них выделяют различные группы сигналов по особенностям их нестационарности.