где q1t1(T1), q0t0(T0) - это время, затраченное на производство всей продукции соответственно в текущем и базисном периодах.

Сводный индекс удельного расхода материалов Im , топлива определяют по формуле



где m1, m0 - удельный расход материалов (топлива), т.е. расход материалов (топлива) на единицу продукции соответственно в текущем и базисном периодах.

Он характеризует, как изменился в среднем расход различных видов материалов, топлива на единицу продукции.

Расчет индексов может быть выполнен в агрегатной форме и форме средних индексов - среднеарифметического взвешенного и среднегармонического. Все вышеприведенные индексы рассчитаны как агрегатные индексы. Выбор формы расчета индексов зависит от наличия исходных данных. Если известны значения индексируемого показателя и веса в текущем и базисном периодах, то пользуются агрегатной формой индексов. Если отсутствуют значения индексируемого показателя или веса в текущем или базисном периодах, но известны изменения индексируемого показателя или веса по отдельным единицам анализируемой совокупности, пользуются формой средних индексов. Например, известны плановый размер затрат по выпуску продукции на предприятии q0z0 и задание по росту выпуска продукции отдельных видов iq. Необходимо определить индекс физического объема продукции Iq. Индекс физического объема продукции определят по формуле



Для решения задачи неизвестен фактический выпуск продукции, но задан рост каждого вида продукции , который определяют по формуле

Отсюда определяем q1:

q1=i_qq₀
Подставляем найденную величину в исходную формулу



Это есть не что иное, как средняя арифметическая взвешенная индекса физического объема. Соответственно индекс называют среднеарифметическим индексом. Или, например, известны размер товарооборота в отчетном q₁

---

p₁ и плановом периодах q₀p₀, а также изменения цен в отчетном периоде относительно планового по отдельным видам изделий i_p. Необходимо определить, как в среднем изменились цены по всем видам изделий, т.е. индекс цен .

Индекс цен определяют по формуле



В нашем примере известен товарооборот в отчетном периоде p₁q₁ , а товарооборота в ценах планового периода нет, но заданы индивидуальные индексы цен по каждому виду изделий , которые определяют по формуле



Отсюда можно определить цены планового периода



Подставляем их в исходную формулу



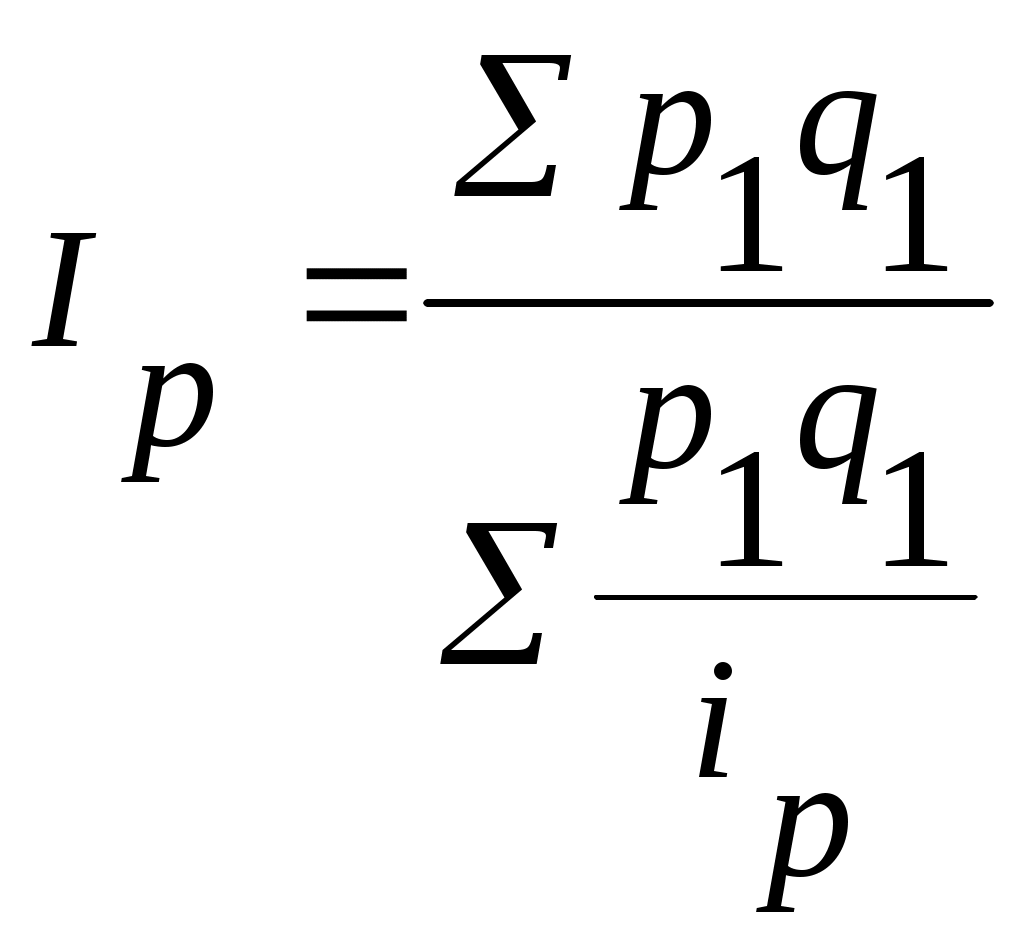
Это есть не что иное, как средняя гармоническая индекса цен. Соответственно его называют среднегармоническим индексом.

Индексы подчиняются той же взаимосвязи, что и характеризуемые ими показатели. Так, например, затраты определяют как произведение себестоимости продукции на объем продукции, соответственно и индекс затрат равен произведению индекса себестоимости и индекса физического объема продукции Iqz=IzIq

Докажем это:



Пользуясь взаимосвязью индексов, можно по величине двух из них определить величину третьего. Например, известно, что по плану на предприятии ожидается рост выпуска физического объема продукции на 18% и снижение себестоимости изделий в среднем на 3%. Необходимо определить изменение затрат на заданный объем работ. Пользуясь взаимосвязью индексов затрат Iqz физического объема Iq и себестоимости Iz определяем изменение затрат

Iqz = Iq Iz= или 114%

Таким образом, индекс затрат составляет 114%, т.е. затраты вырастут на 14%.

Индексы широко используются в факторном анализе для выявления меры влияния факторных показателей на средний уровень определяемого или результативного показателя. Например, необходимо определить, на сколько процентов изменение среднего уровня себестоимости перевозок обусловлено изменением самой себестоимости как таковой и на сколько процентов изменением структуры перевозок. Пусть известны объемы перевозок каждого рода груза и их себестоимость в текущем и базисном периодах, табл.2.(данные условные).

---

Таблица 2 - Динамика объема и себестоимости перевозок грузов

Род груза	Объем перевозок, млн.ткм		Себестоимость перевозок, руб./10 т.км
	базисный период	отчетный период	базисный период	отчетный период
Каменный уголь Руда Строительные материалы	14400 2000 600	17500 2500 1000	4,0 3,0 1,5	5,0 3,5 2,0

Изменение среднего уровня себестоимости определяется как отношение среднего уровня себестоимости перевозок по всем грузам в отчетном и базисном периодах.



Средняя себестоимость, в свою очередь определяется как отношение общих затрат на производство к объему продукции:

,

Сопоставляя средние уровни себестоимости отчетного и базисного периодов наблюдаем изменение двух факторов: себестоимости z и объема перевозок q:



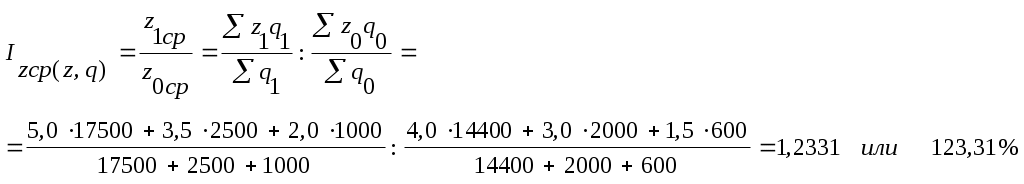
Средняя себестоимость перевозок всех грузов под влиянием роста себестоимости и объема перевозок возросла на 23,31 %. Этот индекс называется индексом переменного состава. Чтобы определить влияние изменения себестоимости перевозок отдельных грузов на среднюю себестоимость перевозок всех грузов, надо исключить влияние структуры перевозок на ее величину. Для этого объемы перевозок берут на одном уровне. Поскольку это объемный показатель, то берем их на уровне отчета.



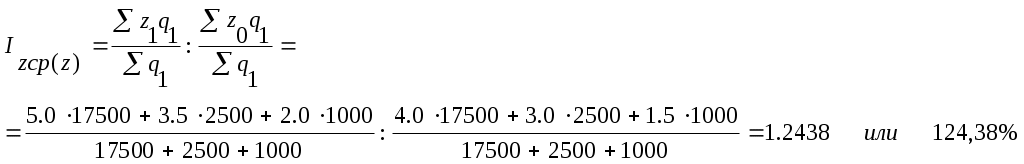
Как показывают расчеты, за счет роста себестоимости перевозок отдельных грузов в среднем себестоимость выросла на 24,38%.

Этот индекс называют индексом постоянного состава, он отражает влияние только индексируемого показателя. По существу это тот же сводный индекс себестоимости:

---

Для оценки влияния изменения объема перевозок по определенным грузам, т.е. влияние структуры перевозок на средний уровень себестоимости грузов, необходимо нивелировать влияние изменения себестоимости перевозок отдельных грузов на ее средний уровень. С этой целью себестоимость перевозки отдельных грузов берем на одном уровне - плановом, поскольку это качественный показатель:



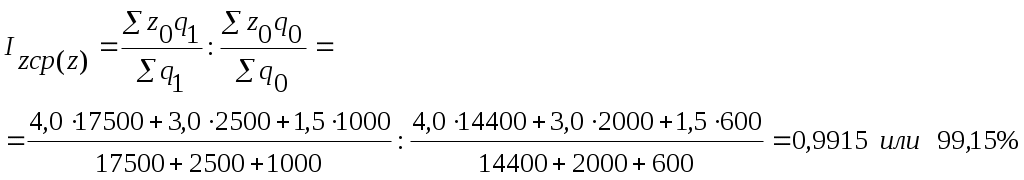
Как показывает расчет, за счет изменения структуры средняя себестоимость перевозок всех грузов снизилась на 0,85 %.

Этот индекс называют индексом структурных сдвигов, он отражает влияние структуры объема работ на средний уровень индексируемого показателя.

Правильность выполнения расчетов можно проверить через взаимосвязь индексов:



Расчеты по задаче должны быть выполнены с применением формул в развернутом виде и сопровождаются пояснениями и описанием результатов расчетов.
Методические указания к заданию 5

Выборочное наблюдение - это один из видов несплошного наблюдения, при котором учету подлежит только часть единиц наблюдаемого явления, и отбор единиц в выборочную совокупность производится по определенному закону. Статистические характеристики, полученные на основе выборочного наблюдения - выборочная средняя, выборочная дисперсия и т.д. всегда отличаются по величине от статистических характеристик генеральной совокупности, охватывающей все единицы изучаемого явления.

Разница статистических характеристик генеральной и выборочной совокупности называется ошибкой выборки или репрезентативности и обозначается



где хср.генер. и хср.выбор. - соответственно генеральная и выборочная средние.

Величина ошибки выборки средней зависит от числа наблюдений составляющих выборочную совокупность и дисперсии изучаемого признака . Чем больше величина выборки n тем ошибка выборки меньше. Чем больше дисперсия значений признака в выборке тем больше ошибка выборки. Аналитически это записывается так:

---

,

Дисперсию доли, как альтернативного признака, определяют по формуле



где w - доля

Соответственно, ошибка доли определяется по формуле



В математической статистике доказано, что с определенной вероятностью р можно утверждать, что при данной дисперсии изучаемого признака и числа наблюдений величина ошибки выборки не превысит определенной заранее заданной величины, называемой предельной ошибкой выборки .

Предельную ошибку средней определяют по формуле



где t - коэффициент доверия (отношение предельной и средней ошибки выборки).

Коэффициент доверия определяется по выписке из таблицы значений функции приведенную в конце настоящих методических указаний.

Предельную ошибку доли определяют по формуле:



В зависимости от способа отбора единицы в выборочную совокупность различают следующие виды выборки:

индивидуальную, серийную;

случайную, механическую, типологическую;

повторную, бесповторную;

При бесповторной выборке единица изучаемого явления может попасть в выборку только один раз, при повторном способе отбора единица изучаемого явления может попасть в выборку нескольких раз. Соответственно, ошибка выборки при бесповторном отборе рассчитывается по формуле:



где N - число единиц в генеральной совокупности:

при повторном отборе - по формуле



Задаваясь определенной допустимой ошибкой выборки с вероятностью ошибки р и зная дисперсию изучаемого признака определяют число единиц n подлежащих отбору в выборочную совокупность при бесповторном отборе (см. табл. 4.1.)

---

Смотрите также файлы

• Контрольная работа по теме вид.docx

• Конспект Проведений целевой тематической прогулки во второй младшей группе специальность 44. 02. 01.docx

• Памятка для родителей. Что делать, если ребёнок стал жертвой кибербуллинга.docx

• Практикум Экосистема сбер.pdf

• Дипломная работа организация процессов приготовления горячих блюд из птицы на базе студенческой столовой. Специальность.docx