Файл: Функции нескольких переменных с примерами решения Функции нескольких переменных.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 64
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Построить линии уровня функции
Решение:
Линия уровня
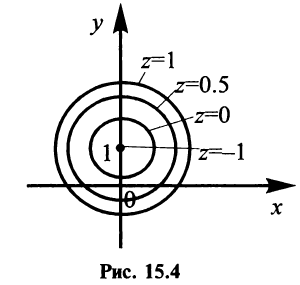
Точка
Предел и непрерывность
Большая часть понятий математического анализа, определенных ранее для функций одной переменной, может быть перенесена на случай двух переменных.
Определение. Число называется пределом функции
(т.е. при
Обозначается предел так:
Пример:
Найти предел
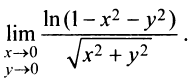
Решение:
Обозначим
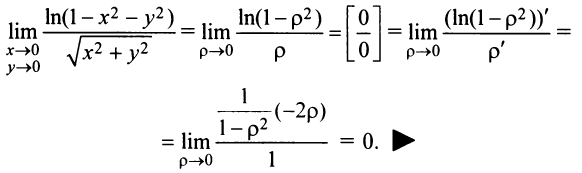
Как правило, вычисление пределов функций двух переменных оказывается существенно более трудной задачей по сравнению со случаем одной переменной. Причина заключается в том, что на прямой существуют всего два направления, по которым аргумент может стремиться к предельной точке — а именно, справа и слева. На плоскости же таких направлений — бесконечное множество, и пределы функции по разным направлениям могут не совпадать.
Пример:
Доказать, что
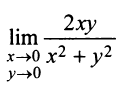 не существует.
не существует.Решение:
Будем приближаться к точке
Если
Получили, что значение предела зависит от углового коэффициента прямой. Но так как предел функции не должен зависеть от способа приближения точки
), то рассматриваемый предел не существует. ►
Определение. Функция
Геометрический смысл непрерывности очевиден: график в точке
Частные производные
Дадим аргументу приращение , аргументу — приращение Тогда функция получит наращенное значение
Полное приращение функции, вообще говоря, не равно сумме частных, т.е.
Пример:
Найти частные и полное приращения функции
Решение:
Получили, что
Определение. Частной производной функции нескольких переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению рассматриваемой независимой переменной при стремлении последнего к нулю (если этот предел существует).
Обозначается частная производная так:
Таким образом, для функции
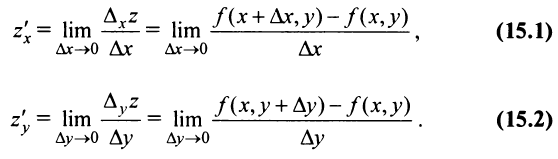
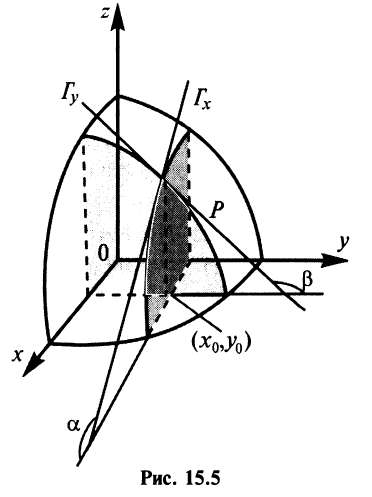
Геометрический смысл частных производных функции
Пусть график функции
В этом случае производная выражает угловой коэффициент касательной к кривой , в заданной точке
Из определения частных производных (15.1), (15.2) следует, что для нахождения производной
Пример:
Найти частные производные функций:
Решение:
а) Чтобы найти частную производную по , считаем постоянной величиной. Таким образом,
б) При фиксированном у имеем степенную функцию от . Таким образом,
Пример:
Поток пассажиров выражается функцией
Решение:
Производная
Дифференциал функции
Дифференциал функции