Файл: Функции нескольких переменных с примерами решения Функции нескольких переменных.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 65
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
определялся как главная, линейная относительно , часть приращения функции, равная произведению 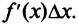
Обобщая определение дифференциала функции на случай двух независимых переменных, приходим к следующему определению.
Определение. Дифференциалом функции называется сумма произведений частных производных этой функции на приращения соответствующих независимых переменных, т.е.

Учитывая, что для функций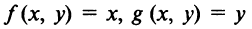 согласно (15.3)
согласно (15.3) 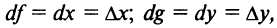 формулу дифференциала (15.3) можно записать в виде
формулу дифференциала (15.3) можно записать в виде

или
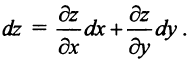
Определение. Функция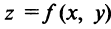 называется дифференцируемой в точке
называется дифференцируемой в точке 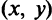 , если ее полное приращение может быть представлено в виде
, если ее полное приращение может быть представлено в виде

где — дифференциал функции,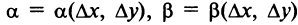 — бесконечно малые при
— бесконечно малые при 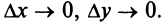
Таким образом, дифференциал функции двух переменных, как и в случае одной переменной, представляет главную, линейную относительно приращений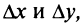 часть полного приращения функции.
часть полного приращения функции.
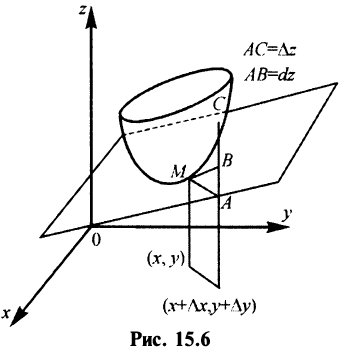
Можно показать, что если полное приращение функции представляет геометрически приращение аппликаты поверхности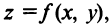
, то дифференциал функции есть приращение аппликаты касательной плоскости к поверхности в данной точке, когда переменные
в данной точке, когда переменные 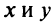 получают приращения
получают приращения 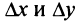 (см. рис. 15.6).
(см. рис. 15.6).
Следует отметить, что для функции одной переменной существование конечной производной
существование конечной производной 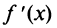 и представление приращения функции в виде (9.1), т.е.
и представление приращения функции в виде (9.1), т.е. 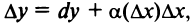 , являются равнозначными утверждениями, и любое из них могло быть взято за определение дифференцируемости функции.
, являются равнозначными утверждениями, и любое из них могло быть взято за определение дифференцируемости функции.
Для функции нескольких переменных дело обстоит иначе: существование частных производных является лишь необходимым, но недостаточным условием дифференцируемости функции.
Следующая теорема выражает достаточное условие дифференцируемости функции двух переменных.
Теорема. Если частные производные функции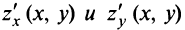 существуют в окрестности точки
существуют в окрестности точки 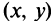 и непрерывны в самой точке
и непрерывны в самой точке 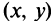 , то функция
, то функция 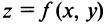 дифференцируема в этой точке.
дифференцируема в этой точке.
Обобщая определение дифференциала функции на случай двух независимых переменных, приходим к следующему определению.
Определение. Дифференциалом функции называется сумма произведений частных производных этой функции на приращения соответствующих независимых переменных, т.е.
Учитывая, что для функций
или
Определение. Функция
где — дифференциал функции,
Таким образом, дифференциал функции двух переменных, как и в случае одной переменной, представляет главную, линейную относительно приращений
Можно показать, что если полное приращение функции представляет геометрически приращение аппликаты поверхности
, то дифференциал функции есть приращение аппликаты касательной плоскости к поверхности

Следует отметить, что для функции одной переменной
Для функции нескольких переменных дело обстоит иначе: существование частных производных является лишь необходимым, но недостаточным условием дифференцируемости функции.
Следующая теорема выражает достаточное условие дифференцируемости функции двух переменных.
Теорема. Если частные производные функции