ЗДРАВСТВУЙТЕ ! Я ученик 9 класса школы №11 г. Дербент Асрян Самвел..Моя исследовательская работа называется

«Способы решения кубических уравнений».

Решение различных алгебраических и геометрических задач сводится к какому-либо уравнению. Уравнения мы встречаем также при решении практических задач. Мы подробно изучили правила решения линейных уравнений, формулы связанные с решением квадратных уравнений. А вот уравнениям третьей степени уделялось на уроках математики очень мало времени и решали графическим способом или методом разложения на множители.

Актуальность темы состоит в следующем: решение квадратного уравнения – знакомая процедура, идущая по формулам. Логичны вопросы: существует ли, наряду с этим алгоритмом, алгоритм вычисления корней кубического уравнения? Какие способы решения кубических уравнений применяются на практике?

Далее нас заинтересовали вопросы: 1) доказана ли формула для корней уравнения третьей степени, т.е. можно ли найти корни кубического уравнения, выполняя конечное число операций над коэффициентами такого уравнения. А удивительная теорема Франсуа Виета применима ли к кубическим уравнениям? Ознакомившись со справочной литературой, я выяснил, что формула для вычисления корней кубического уравнения существует, но она применяется редко. И мне захотелось узнать причину такой непопулярности формулы Кардано. Ведь итальянский математик Джироламо Кардано опубликовал эту формулу в книге «Великое искусство, или о правилах алгебры» в 1545 году. Однако нашей главной задачей в ходе работы стало нахождение более рационального способа для решения уравнений третьей степени.

Объект исследования–кубическое уравнение.

Предмет исследования - различные способы решения кубических уравнений.

Гипотеза - предположение о том, что существует связь между коэффициентами кубического уравнения и его корнями, и при решении таких уравнений можно применять разнообразные способы.

Цель работы – выявление связи между коэффициентами кубического уравнения и его корнями, систематизирование знаний о способах решения кубических уравнений, классификация кубических уравнений по методам и приемам их решений.

---

Задачи:

-анализ школьных учебников;

- анализ научной и справочной литературы;

- рассмотреть аналог теоремы Виета для уравнения третьей степени;

-рассмотреть формулу Кардано для уравнения третьей степени;

-рассмотреть элементарные способы и приемы решения кубических уравнений и сравнить их по степени сложности.

Так как в учебниках[1,3],большинство рассуждений и доказательств проводится не на конкретных примерах, а в общем виде, то я решил искать частные примеры, подтверждающие или опровергающие мою мысль. Рассмотрев немало практических примеров, мне удалось в результате исследования сделать выводы о причинах непопулярности формулы Кардано и о существовании рациональных способов решения кубических уравнений.

Первые попытки найти решения задач, сводящихся к кубическим уравнениям, были сделаны математиками древности (например, задачи об удвоении куба и трисекции угла). Математики средневековья создали довольно развитую теорию кубических уравнений. В Европе впервые в тригонометрической форме решение одного случая кубического уравнения дал Ф.Виет (1593г.). Первое решение в радикалах одного из видов кубических уравнений удалось найти С.Ферро (около 1515 г.), однако оно не было опубликовано. Открытие независимо повторил Н. Тарталья (1535г.), указав правило решения еще двух других видов кубических уравнений. Опубликованы эти открытия были в 1545 году Дж. Кардано, который упомянул об авторстве Н. Тартальи. Я изучил историю этих открытий и понял , что даже авторство найденных формул недостаточно ясно.

Методы исследования:

-изучение литературных и интернет- ресурсов;

- анализ и классификация информации;

-сравнение различных видов уравнений и их классификация;

-сравнение способов решения кубических уравнений;

-обобщение.

Работа состоит из введения, четырех глав основной экспериментальной части, заключения, списка литературы и приложений.
Основная часть

1. 
   Кубическое уравнение.
   

Кубическим уравнением называется уравнение вида: ax³+bx+cx+d=0 (1), где x-переменная, a,b,c,d, - некоторые числа, где а≠0.Число х, обращающее уравнение в верное равенство, называется корнем или решением уравнения. Оно также является корнем многочлена третьей степени, стоящего в левой части уравнения.Если а=1,то уравнение называют приведенным кубическим уравнением: х

---

³+bх²+cx+d=0 (2). Согласно основной теореме алгебры, кубическое уравнение может иметь три корня (с учетом кратности). Из справочной литературы я узнал, что для кубических уравнений тоже существует дискриминант, как и для квадратных уравнений, с помощью которого различаются три случая существования корней кубического уравнения (1).

Для приведенного квадратного уравнения

x²+px+q=0, если х₁ и х₂ – его корни, то х²+рх+q= (х-х₁)(х-х₂); х²+рх+q= х²-(х₁+х₂)*х+х₁+х₂,

т.е. х₁+х₂= -р, х₁*х₂=q.Это верно, так как два многочлена равны тогда и только тогда, когда равны их коэффициенты при соответствующих степенях переменной.

Рассуждая аналогичным образом, я убедился, что теорема Виета верна и для кубического уравнения (2).

Пусть х₁, х₂, х₃ – корни этого уравнения, тогда справедливо равенство х³+bх²+сх+d = (х-х₁)*(х-х₂)*(х-х₃).

Преобразуем его правую часть: (х-х₁)*(х-х₂)*(х-х₃)=х³-(х₁+х₂+х₃) * х²+(х₁х₂+х₁х₃+х₂х₃) *х-х₁х₂х₃.Сравнивая коэффициенты при одинаковых степенях х, получим систему равенств:

х₁+х₂+х₃= -b,

х₁х₂+х₁х₃+х

---

₂х₃=с,

х₁*х₂*х₃= -d.

Верна и теорема, обратная теореме Виета. Если числа х₁,х₂,х₃ таковы, что

х₁+х₂+х₃= -b,

х₁х₂+х₁х₃+х₂х₃=с,

х₁*х₂*х₃= -d,

то эти числа являются корнями уравнения х³+bх²+сх+d=0. А корни кубического уравнения (1) связаны с его коэффициентами a,b,c,d следующим образом:

х₁+х₂+х₃= - ,

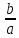х₁х₂+х₁х₃+х₂х₃= ,корень, если он существует, надо искать среди делителей свободного члена – числа х₁*х₂*х₃= - ,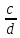

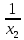+ + = - , d≠0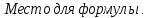



( Дальще по презентации примеры.)

Мне удалось выделить основные виды кубических уравнений и практические способы их решения. Еще я пришел к выводу, что использовать формулу Кардано для решения кубических уравнений не всегда целесообразно. Когда уравнение имеет три решения, выражение под квадратным корнем в формуле Кардано отрицательно. Если уравнение имеет всего одно решение, формула его и дает. Значит, причина непопулярности формулы (6) не только в её громоздкости, а в её ненадежности. Тогда зачем же она нужна? Дело в том, что формула (6) дает ответ на классический вопрос о «разрешимости уравнений третьей степени в радикалах». Это означает, что для решения уравнений третьей степени с целыми коэффициентами вполне хватает запаса рациональных чисел, расширенного корнями разных степеней.

---

Вывод. Решать кубические уравнения рациональнее, используя способы, разобранные в главе 4 основной части данной работы. Формулу Кардано удобно применять при решении кубических уравнений с параметром.

Во втором полугодии 9 класса мы изучали элективный курс «Тайны решения уравнений», на занятиях которого и познакомились с более интересными способами решения различных уравнений, в том числе и кубических. В конце изучения элективного курса мы провели эксперимент по практическому применению исследованных способов: 20 учащихся 9 класса получили задание решить кубическое уравнение х³ – 6х² + 11х -6 = 0 тремя способами:

1. C помощью формулы Кардано верно решили 5 человек.

2. Графическим способом верно решили 15 человек.

3. С помощью разложения на множители верно решили 18 человек.

Выводы о практическом применении способов решения кубических уравнений четко демонстрирует диаграмма (прил. рис.3).Считаю, что тема, которая меня заинтересовала достаточно многогранна и перспективна, можно продолжить исследование способов решения уравнений высших степеней. Результаты работы можно использовать для углубленного изучения данной темы на уроках и занятиях элективных курсов, для подготовки к ГИА и к олимпиадам учащимися 9-11 классов.

---

Смотрите также файлы

• Основная образовательная программа направления подготовки Клиническая психология 3.doc

• Русский язык соо (1 часть).odt

• Публицистический стиль.docx

• Курсовой проект по мдк 02. 02. Внутреннее электроснабжение промышленных и гражданских зданий.docx

• Подготовка к практике. В данном разделе содержится информация о том, на основании каких документов и в каких организациях Вам необходимо проходить практику, кто будет курировать процесс прохождения практики. Раздел Прохождение практики.docx