Реактивті қозғалыс принципі – зымыран қозғалысына мысал келтірсек. Қарапайым зымыран жану камерасы бар отын толтырған қабықтан тұрады. Отынның жануа кезінде жоғарғы температураға дейінгі қызған жоғары қысымдағы газ Сопло деп аталатын ерекше пішіні бар камерадан үлкен жылдамдықпен (4км/с-қа дейінгі) атқылап шығады.Есептеуді жеңілдету үшін қабықша ішіндегі отын түгел жанады да, жану өнімдері mv1 импульс алады деп есептейік, мұндағы v1 – атқылап шығатын газ жылдамдығы, m – жанған отынның массасы. Газ бен зымыранның өзара әрекеттесуі кезіндегі күштер сыртқы күштермен салыстырғанда өте үлкен болғандықтан, «зымыран – газ» жүйесін тұйық жүйе деп есептеуге болады. Бұлай қарастыру жүйеге импульстің сақталу заңын қолдануға мүмкіндік береді. Мәре алдындағы зымыранның сыртқы қабығымен және отынның қоса есептегендегі массасы М болсын. Онда газ сыртқа атқылап шыққаннан кейін де денелер жүйесінің қорытқы импульсі өзгермейді. Онда массасы М- m болатын зымыран қабығы модулі бойынша тең, бірақ газ импульсінің бағытына қарама – қарсы бағытталған (М – m) v2 импульс алады, мұндағы v2 – зымыран қабығының жылдамдығы, Онда mv1 = - (М – m) v2 болады. Ал бұдан v2 = - mv/(М- m)

ЛЕКЦИЯ №3

Салыстырмалылықтың арнайы теориясының элементтері.

Тұтас орта механикасының элементтері.

1. 
   Эйнштейн постулаттары.
   
2. 
   Лоренц түрлендірулері.
   
3. 
   Сұйықтағы және газдағы қысым.
   
4. 
   Бернулли теңдеуі.
   
5. 
   Сұйықтардың газдардың ламинарлық және турбуленттік ағыс режимдері.
   

Классикалық динамикада механикалық салыстырмалылық принципі орындалады (Галилейдің салыстырмалылық принципі) : барлық инерциялық жүйелерде механиканың заңдары біркелкі.

Арнайы салыстырмалылық теория негіздерінде Эйнштейн принциптері жатыр:

1.Салыстырмалылық принципі бойынша барлық инерциялық жүйелерде табиғаттың заңдары бірдей.

2.Жарық жылдамдығының тұрақтылық принципі бойынша жарықтың вакуумдегі жылдамдығы барлық инерциалдық жүйелерде бірдей, ол жарық көзі мен қабылдаушысының қозғалысына байланысты емес.
Классикалық механикада Галилей түрлендірулері орындалады,ол бойынша

,

---

, , (3.1)

,

Мұндағы қозғалмайтын К инерциал жүйесіндегі нүктенің координаттары К жүйесімен салыстырғанда тұрақты және түзу сызықты жылдамдықпен қозғалушы инерциал жүйесіндегі координаттары - жылдамдық векторының осьтеріне проекциялары, t- уақыт, нүктенің жүйелеріне салыстырғанда жылдамдықтары.

Лоренц түрлендірулері:

(3.2) 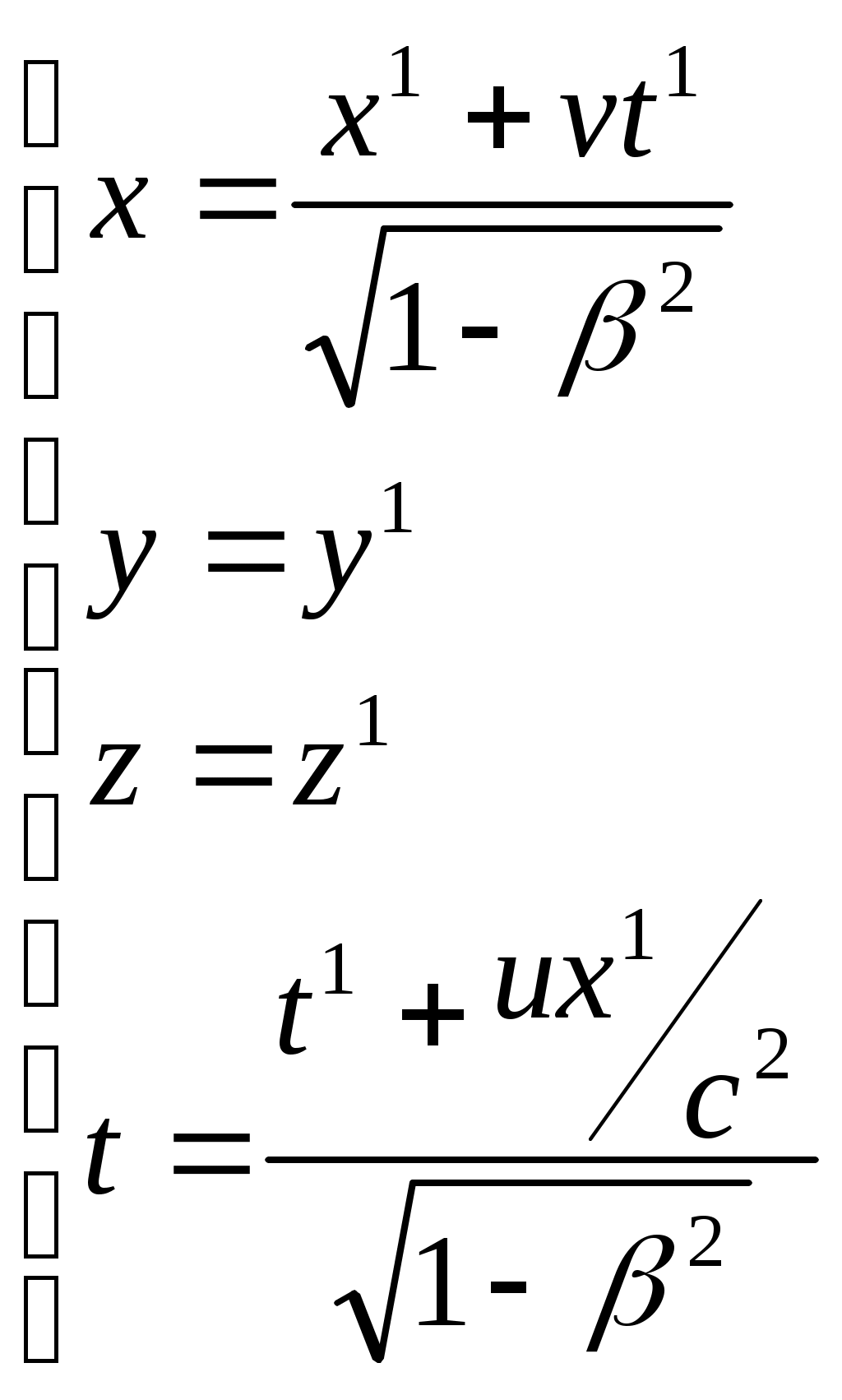мұндағы

Бұл түрлендірулерден

(3.3) ұзындықтың өзгеруі

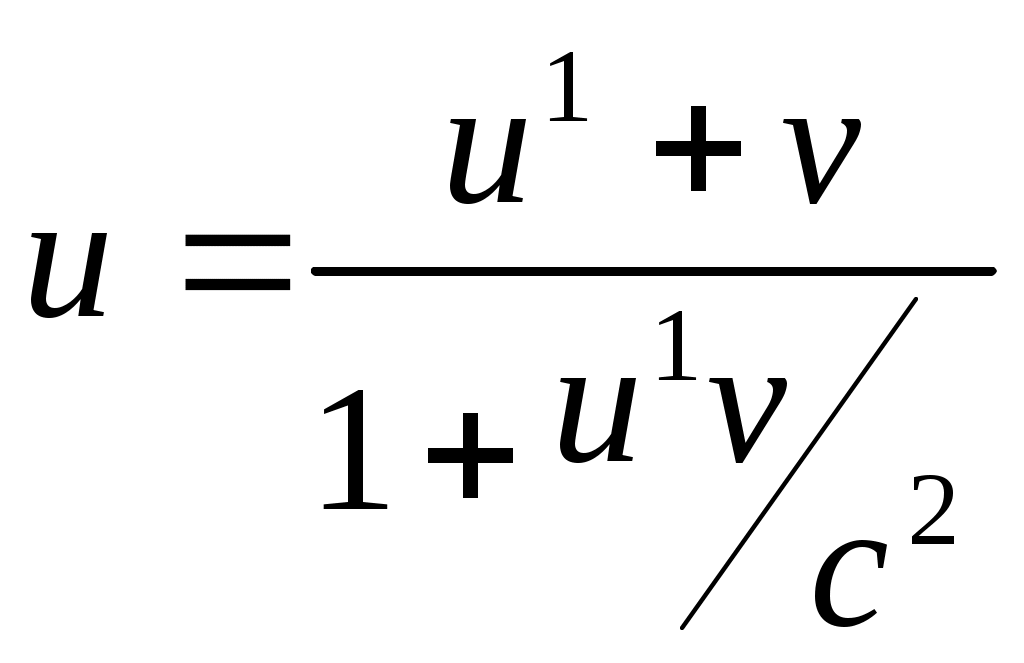(3.4) жылдамдықтар қосу заңы

Қозғалыстағы дененің релятивтік массасы

(3.5)

Релятивтік динамиканың негізгі заңы

(3.6)

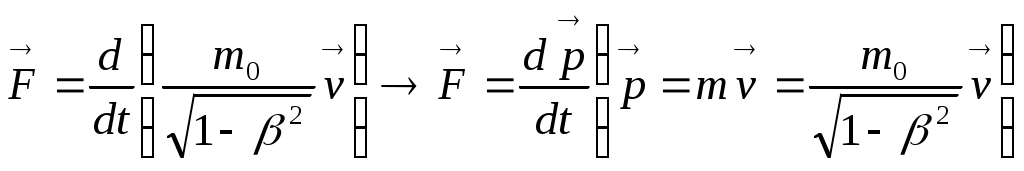
Сұйықтың қысымы деп

(3.7)

шаманы айтады.Мұндағы сұйықтың ауданға нормаль бағытта әсер етуші күш.

Өлшем бірлігі –паскаль(Па) 1Па=

---

Гидростатикалық қысым

(3.8)

-сұйықтың тығыздығы ,h-оның денгейі.
Үзіліссіздік теңдеуі :

(3.9)

Белгілеулер суретте
Б ернулли теңдеуі:

(3.10)

-статикалық қысым

-гидростатикалық қысым

-гидродинамикалық қысым
(3.11) - толық қысым дейді.

Ішкі үйкеліс күші.

(3.12)

-жылдамдық градиенті ,s- сұйықтық беттін ауданы.

-тұтқырлық коэффиценті,өлшем бірлігі-Па*с
Сұйықтың ағысы екі түрлі болады:

Ламинарлық-егер ағым бойынша әрбір жұқа қатар көрші қатарлармен араласпай қозғалса.

Турбуленттік(қүйынды)-егер ағында интенсивті құйындар пайда болады және сұйықтық араласа береді.

Ағын түрі өлшем бірлігі жоқ Рейнольдс санына байланысты

(3.13)

Мұндағы -кинетикалық тұтқырлық , -сұйықтық тығыздығы, -сұйықтың труба қимасы бойынша орташа жылдамдығы,сипаттамалы ұзындық өлшем (мыс.-труба диаметрі)

---

болғанда ағын ламинарлы

- ламинарлықтан турбуленттікке өтеді

- турбуленттік

Стокс өрнегі

(3.14)

F- кедергі күші (сұйықтықтағы қозғалыста денеге)

-тұтқырлық коэффиценті , -шарик радиусы, -оның жылдамдығы.

Пуазейль формуласы:

(3.15)

- капилляр радиусы, -оның ұзындығы, -қысым айырмасы , - t уақытта капиллярдан өткен сұйықтық көлемі .
ЛЕКЦИЯ №4

Тербелістер мен толқындар.

1. 
   Гармониялық тербелістер және олардың сипаттамалары.
   
2. 
   Резонанс.
   
3. 
   Толқындар: анықтамасы және негізгі сипаттамалары.
   
4. 
   Доплер эффектісі.
   
5. 
   Дыбыс. Ультрадыбыс.
   

Гармониялық тербеліс деп-уақыт бойынша қайталанатын қозалыс немесе процесстерді айтады.

Егер тербелістер бастапқы берілген энергия есебінен болып тұрса бұндай тербелісті еркін д.а.,тербеліп түрған шама синус(косинус)заңы бойынша өзгеріп тұрса оны гармоникалық тербеліс деп атайды.

Гармоникалық тербеліс

(4.1)

түсті функциямен өрнектеледі.

Мұндағы: -тербеліп тұрған шаманың максимал мәні-амплитудасы.д.а.

---

- дөңгелектік(циклдік)жиілігі, -бастапқы фаза, - уақыт моментіндегі тербеліс фазасы.

Гармоникалық тербелістерге серіппедегі жүктің ,математикалық, физикалық маятниктердің тербелістері мысал бола алады.

Тербеліс периоды (Т)деп толық бір тербеліске кеткен уақытты айтады.

-уақыт бірлігінде жасалатын толық тербелістер санын тербеліс жиілігі дейді. Жиілік бірлігі –герц(Гц). 1Гц=1/с

(4.2)

Гармоникалық тербелістің дифференциал теңдеуі:

(4.3)

Математикалық маятниктің тербеліс периоды

(4.4) -маятник ұзындығы.

Физикалық маятниктің тербеліс периоды

(4.5)

Мұндағы -іліну нүктесі бойынша есептелінген инерция моменті, -оның келтірілген ұзындығы.

Бір бағыттағы бір жиілікті екі тербелісті қосқанда:

(4.6)

- жаңа гармониялық тербеліс пайда болады.мұндағы



(4.7)

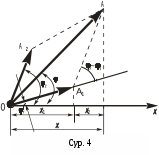
Жиіліктері жақын болған екі гармониялық тербелістерді қосқанда нәтижелеуші тербелістің амплитудасы белгілі бір периодпен өзгеріп тұруын соғу дейді. Гармониялық тербелістерді векторлық диаграммалар методын пайдаланып графикалық түрде кескіндейді. Ол үшін ұзындығы А болған векторды О нүкте арқылы

---

Смотрите также файлы

• Использование облачных технологий google docs (таблицы) и форма google в образовательном процессе аннотация.docx

• Законы Менделя Хромосомная теория Взаимодействие генов Изменчивость Наследственные болезни.docx

• Діагностика та лікування захворювань внутрішніх органів у людей похилого віку.pdf

• При выполнении задания студент должен.docx

• Тема Целостный педагогический процесс.docx