Файл: растырандар Сакипов Н. З., Беркутбаева Р. А., Сугирбекова А. К. Дрістік кешен Физика пні бойынша бб тобы.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 229
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ЛЕКЦИЯ №11
Электромагниттік тербелістер. Айнымалы ток.
-
Тербелмелі контур.
-
Айнымалы электр тоғы.
-
Кернеулер және токтар резонансы.
-
Электромагниттік өріс үшін толқындық теңдеу.
-
Электромагниттік энергияның ток тығыздығы.
Электромагниттік тербелістер кезінде электр шамалар ( зарядтар, токтар ) периодты өзгеріп тұрады және олармен бірге электр және магнит өрістері бір-біріне айналып тұрады. Электромагниттік тербелісті қоздыру және сақтап тұру үшін тербелмелі контур пайдаланады ол тізбектеліп, жалғанған индуктивтілік (L), сиымдылығы C болған конденсатор және кедергісі R болған резистордан тұрады. Тербелмелі контурдағы заряд тербелісінің дифференциал теңдеуі:
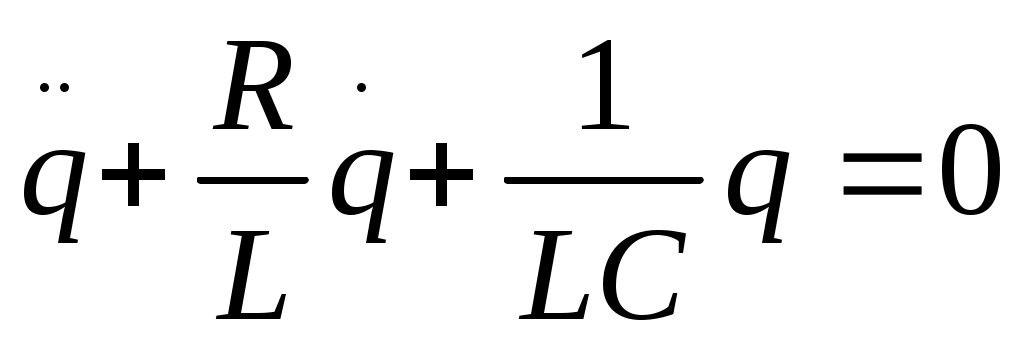 (11.1)
(11.1)
Бұл өшуші еркін тербеліс.
Тербелмелі контурдың меншікті жиілігі (R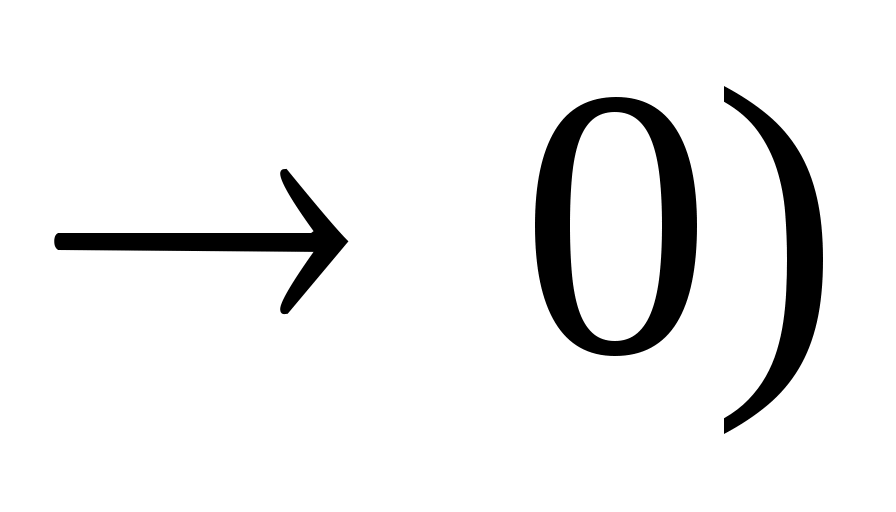
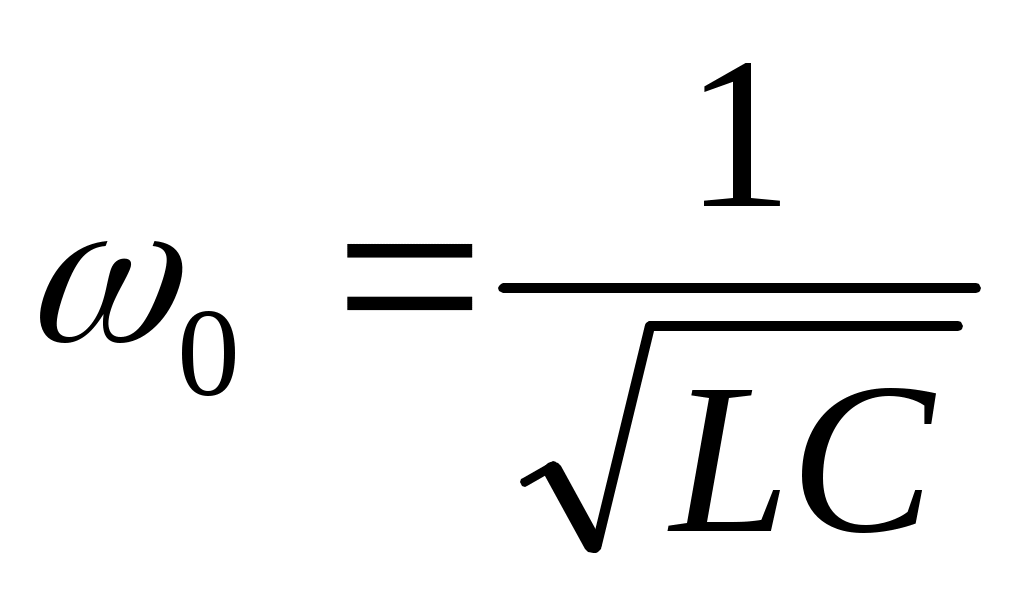 (11.2)
(11.2)
ал периоды
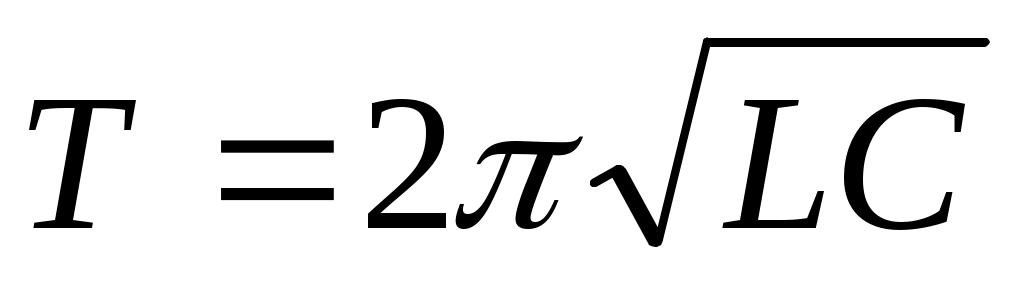 (11.3)
(11.3)
(11.3) формуласы Томсон формуласы деп аталады.
Тербелмелі контурдағы еріксіз тербеліс заңы:
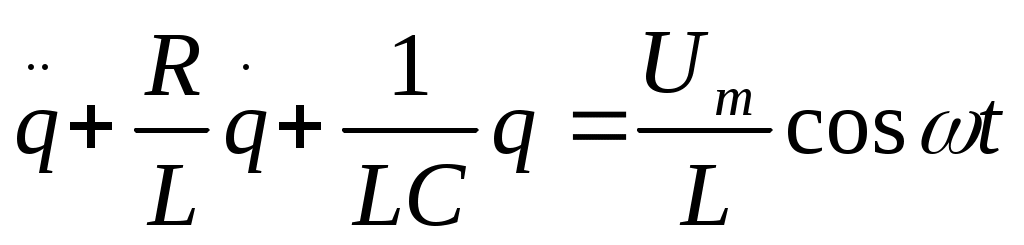 (11.4)
(11.4)
Бұл теңдеудің шешуі:
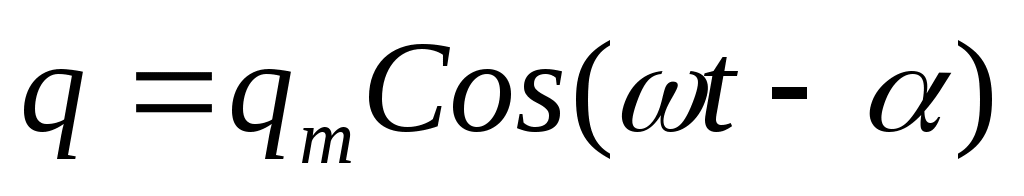 (11.5)
(11.5)
мұндағы
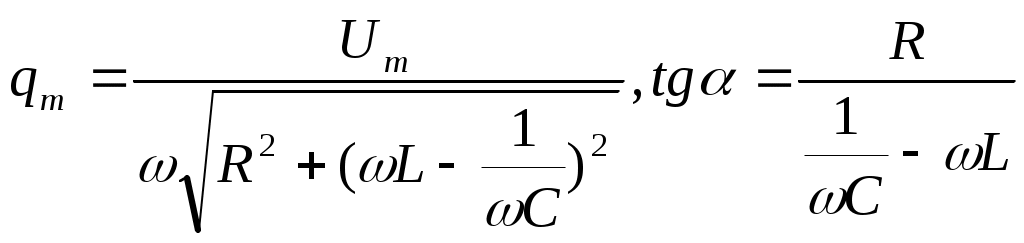 (11.6)
(11.6)
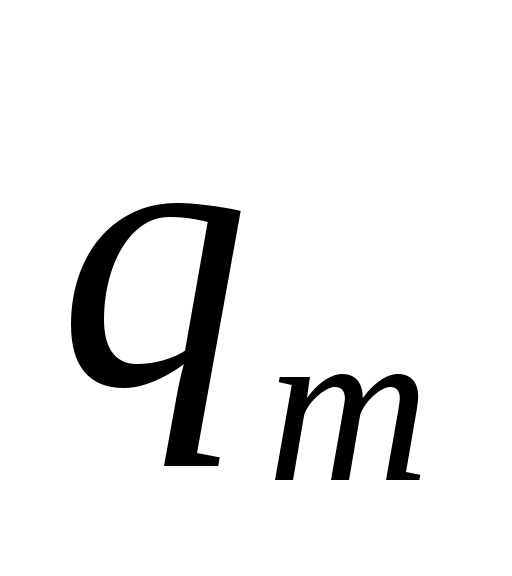 мәні жиілікке байланысты,
мәні жиілікке байланысты, 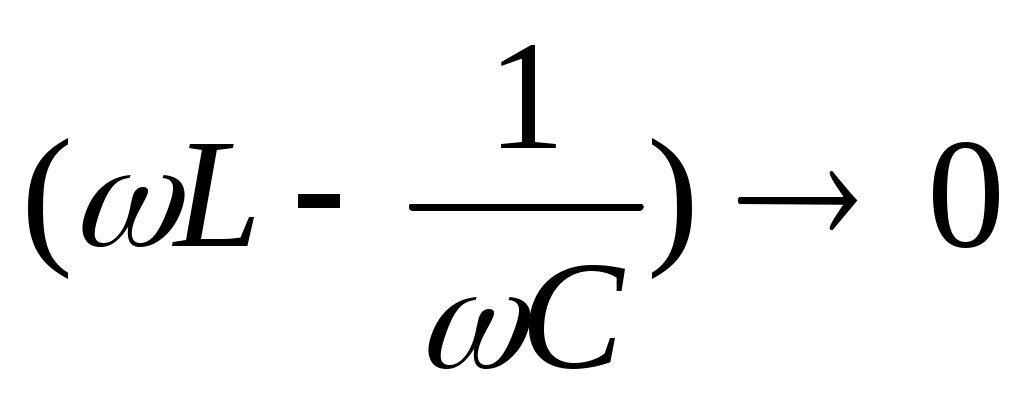 болғанда
болғанда 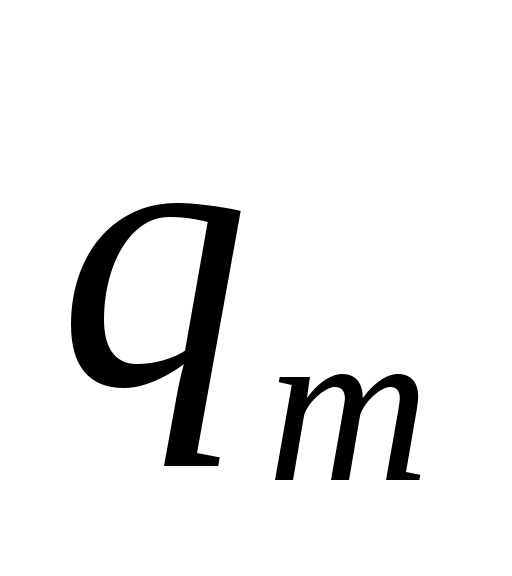 шамасы ең үлкен мәнге ие
шамасы ең үлкен мәнге ие 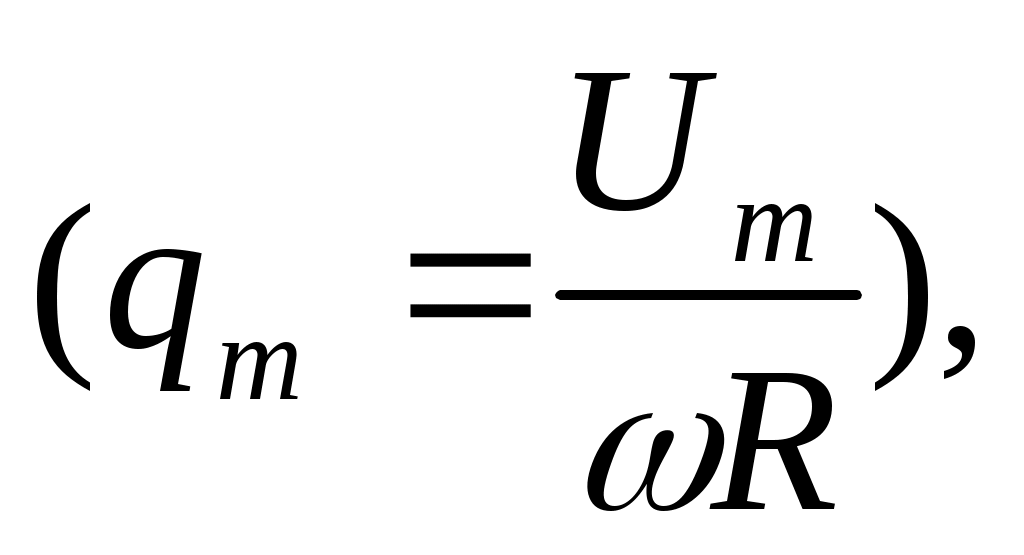 бұл құбылысты резонанс деп атайды.
бұл құбылысты резонанс деп атайды.
Егер тізбекке [оның құрамында резистор, индуктивтілік катушка және конденсатор бар] өзгеруші кернеу
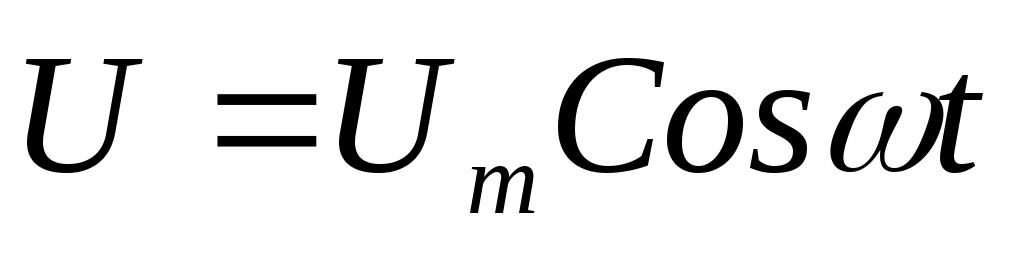 (11.8)
(11.8)
жалғанған болса, онда айнымалы ток өтеді, мұндағы 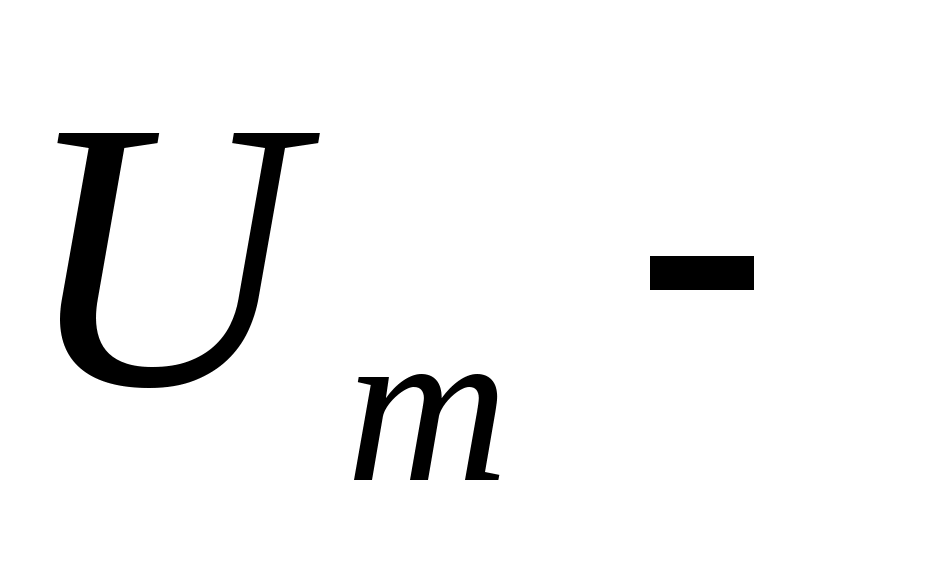 кернеу амплитудасы.
кернеу амплитудасы.
Резистордан айнымалы ток өткенде, ток күші
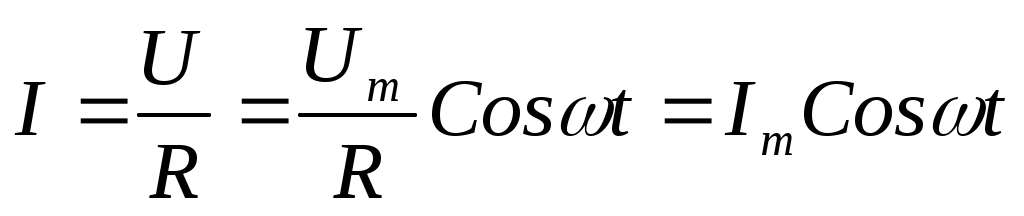 (11.8*)
(11.8*)
Заң бойынша өзгереді.
Мұндағы 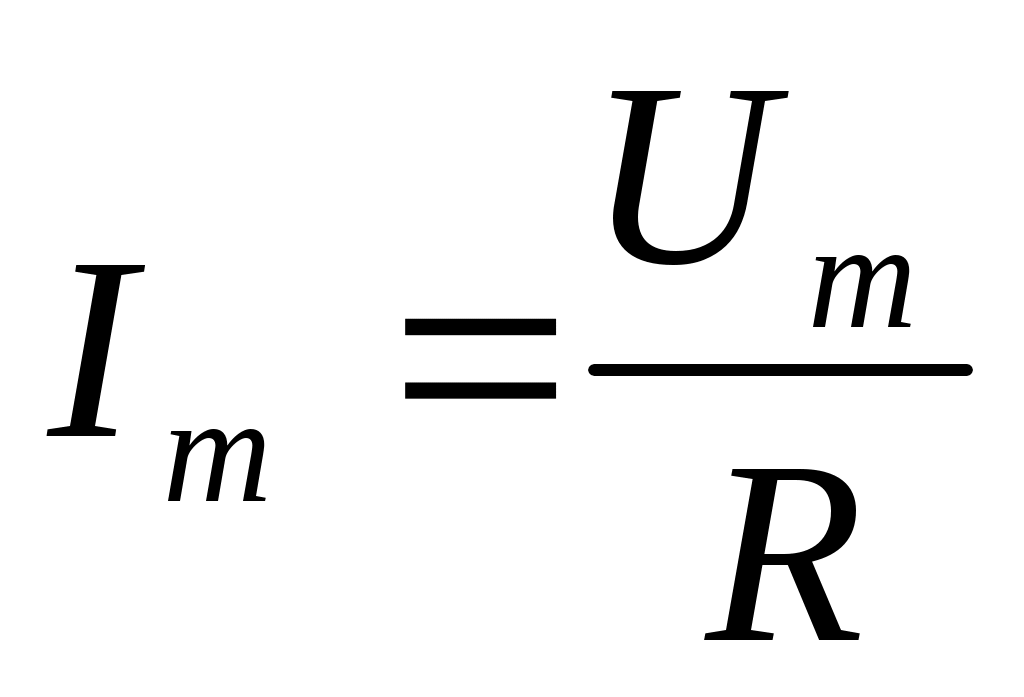 ток күшінің амплитудалық шамасы.
ток күшінің амплитудалық шамасы.
Айнымалы ток индуктивтілік шарғыдан өткенде, ток күші:
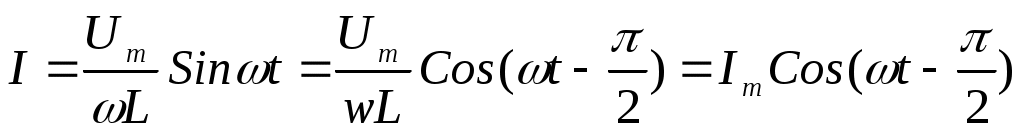 (11.9)
(11.9)
мұндағы 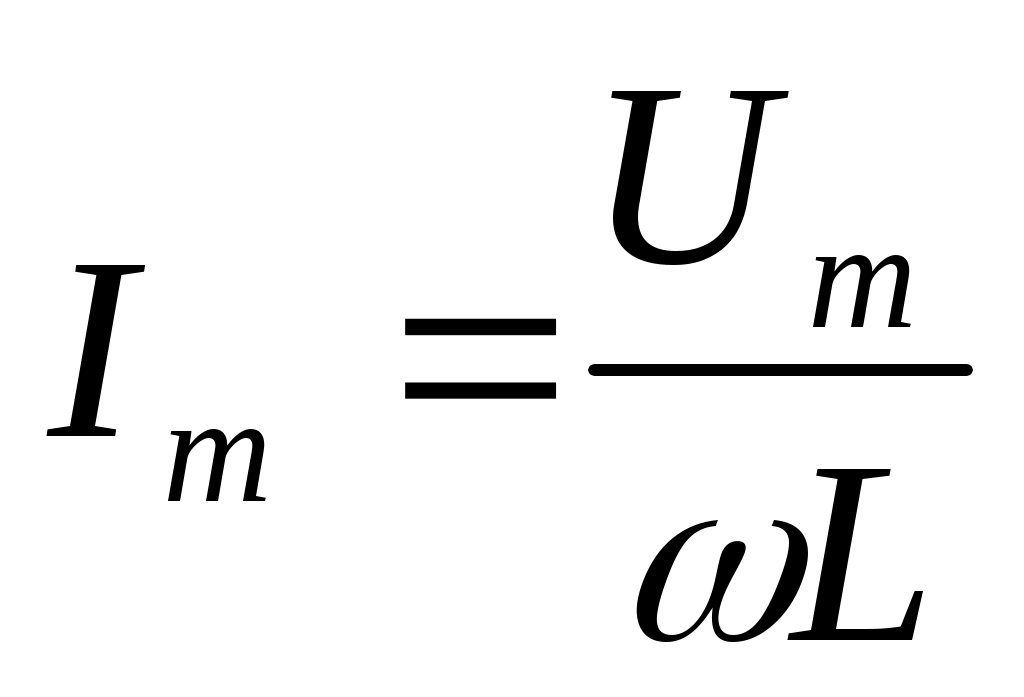 ток күшінің амплитудалық шамасы
ток күшінің амплитудалық шамасы 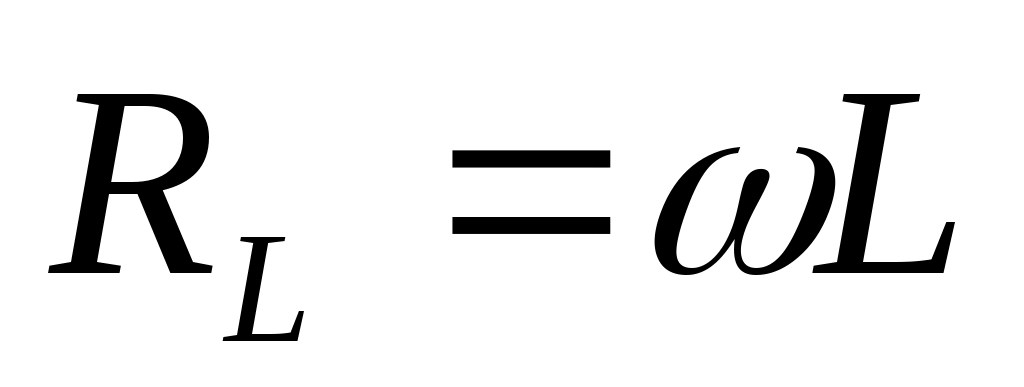 (11.10) шамасы реактивті индуктивті кедергі ( индуктивті кедергі ) деп аталады. Осы шарғыға түсіп тұрған кернеу
(11.10) шамасы реактивті индуктивті кедергі ( индуктивті кедергі ) деп аталады. Осы шарғыға түсіп тұрған кернеу
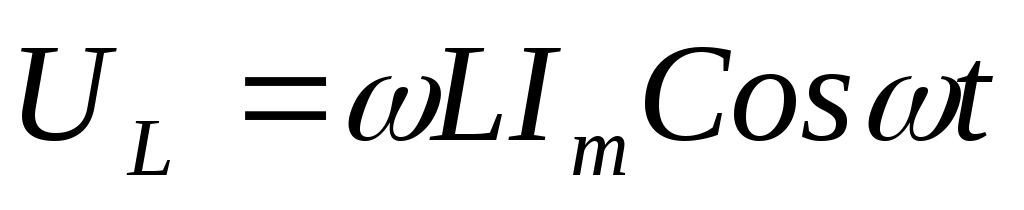 (11.11)
(11.11)
Конденсатордан айнымалы ток өткенде ток күші
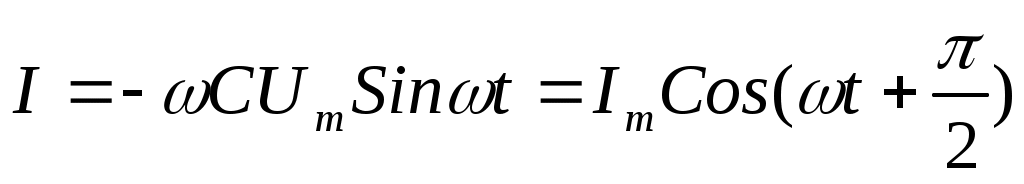 (11.12)
(11.12)
мұндағы
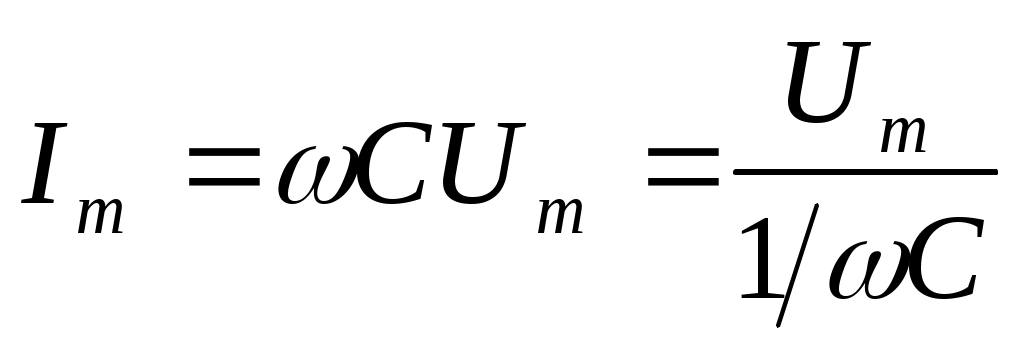 (11.13)
(11.13)
ток күшінің амплитудалық шамасы
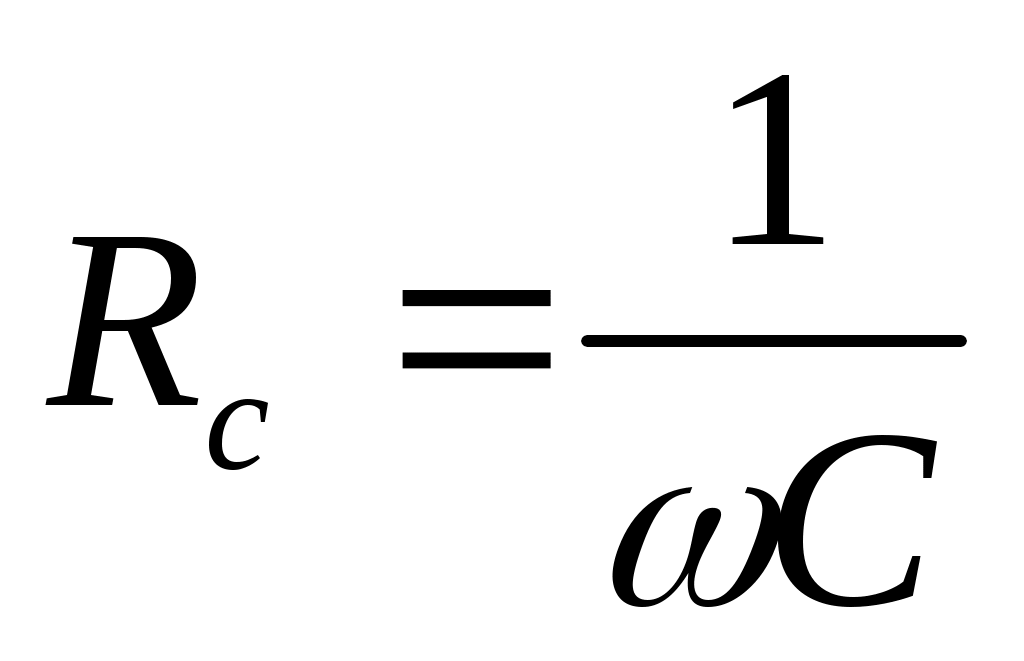 реактивті сиымдылық кедергі ( сиымдылық кедергі ) деп аталады.
реактивті сиымдылық кедергі ( сиымдылық кедергі ) деп аталады.
Конденсаторға түсетін кернеу
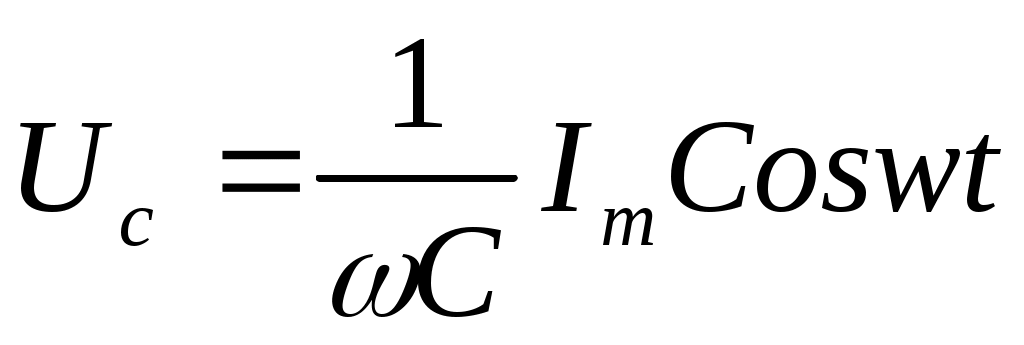 (11.14)
(11.14)
Тізбектеліп жалғанған редистор, шарғы, конденсатор бар тізбектен айнымалы ток өткенде ток күші
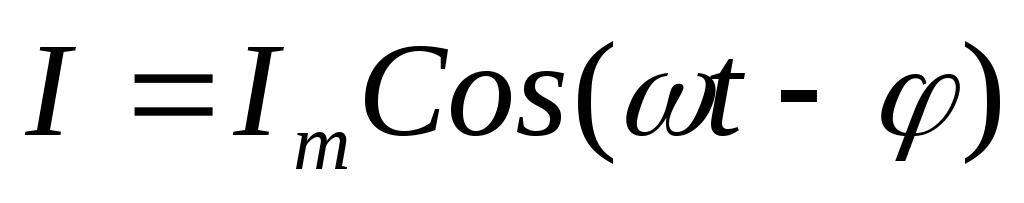 (11.15)
(11.15)
болады, мұндағы
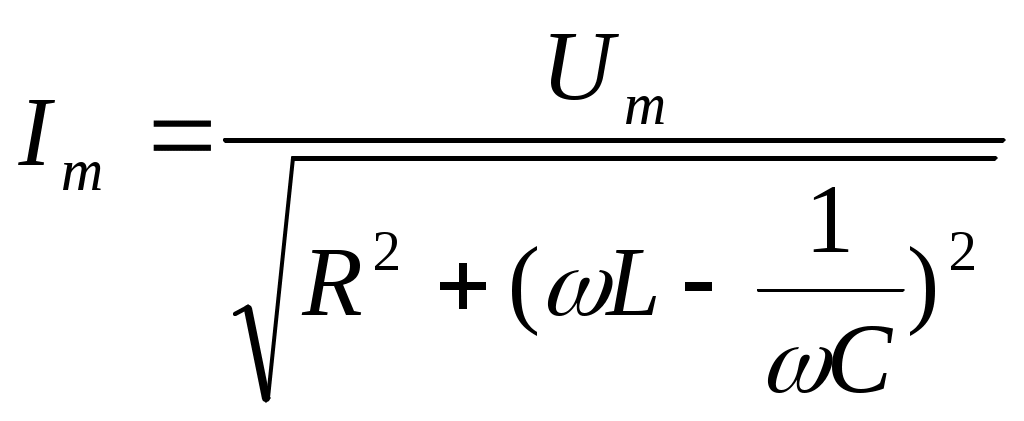 (11.16)
(11.16)
ток күшінің амплитудалық шамасы, кернеу мен ток күші фазалар айырымы
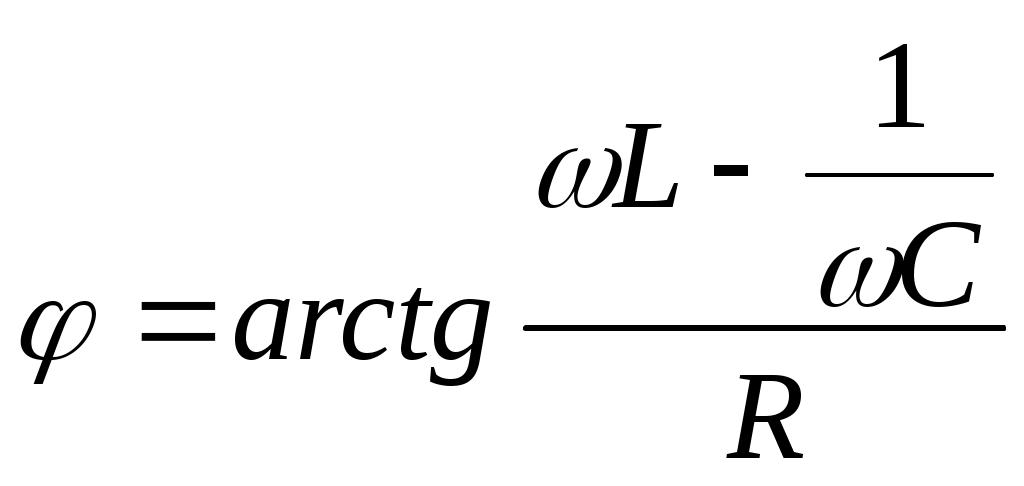 (11.17)
(11.17)
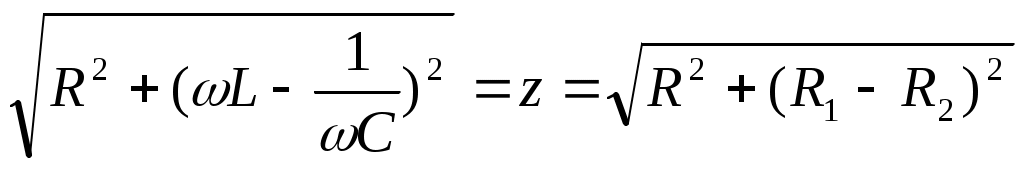 (11.18)
(11.18)
шама тізбектің толық кедергісі деп аталынады.
Айнымалы ток үшін Ом заңы
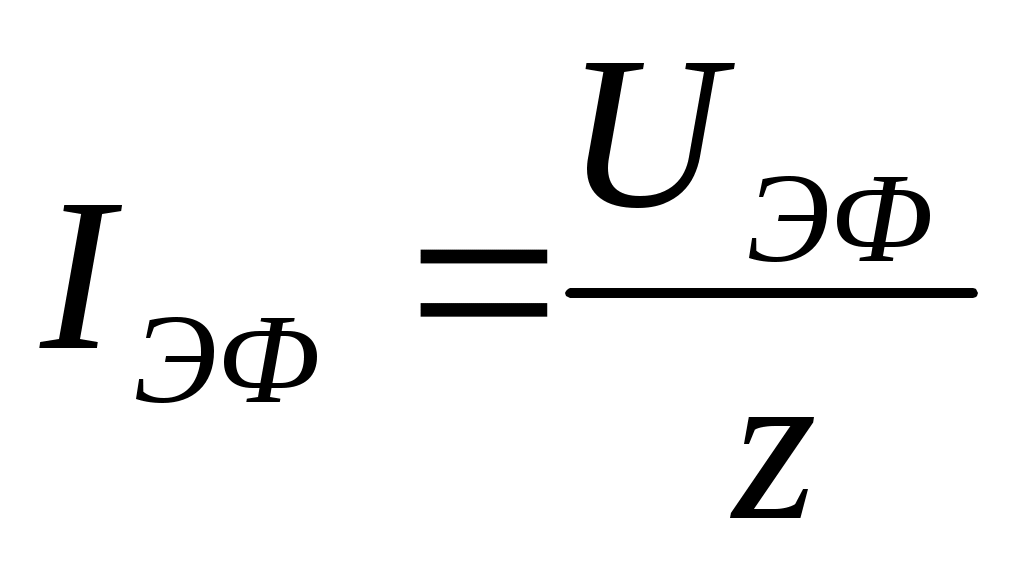 (11.19)
(11.19)
түрінде жазылады, мұндағы
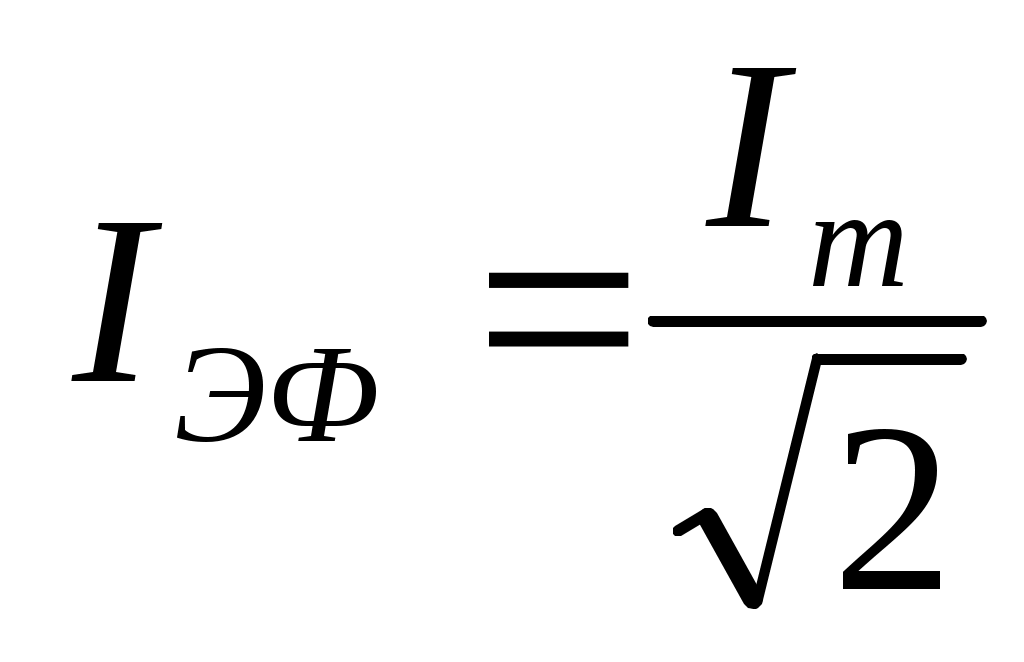 (11.20)
(11.20)
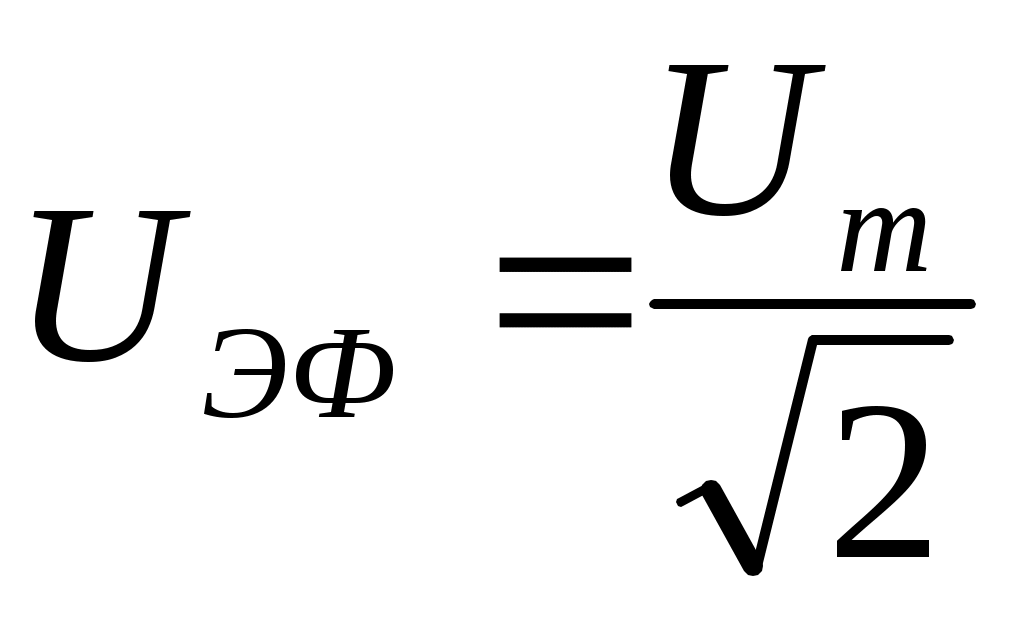 (11.20*)
(11.20*)
ток күші мен кернеудің эффективті мәндері деп аталады.
Айнымалы ток қуаты
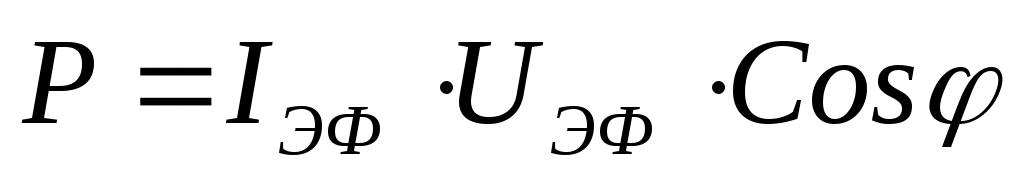 (11.21)
(11.21)
Егер
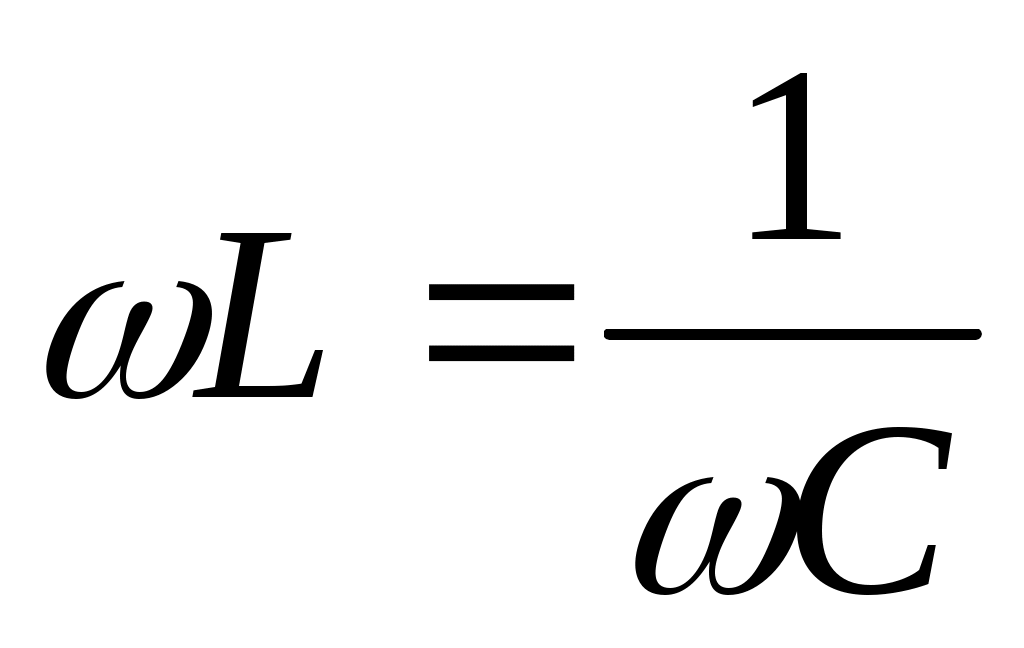 (11.22)
(11.22)
болса тізбектеліп жалғанған конденсатор 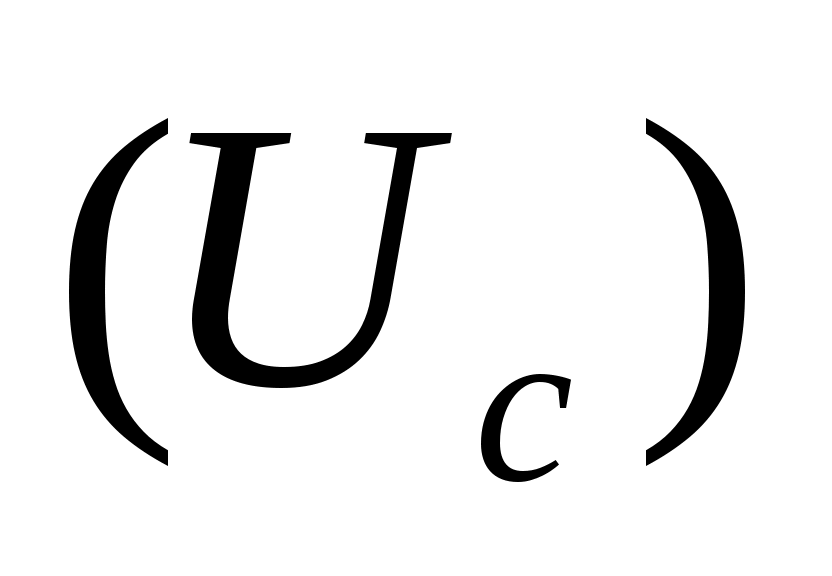 мен шарғыда
мен шарғыда 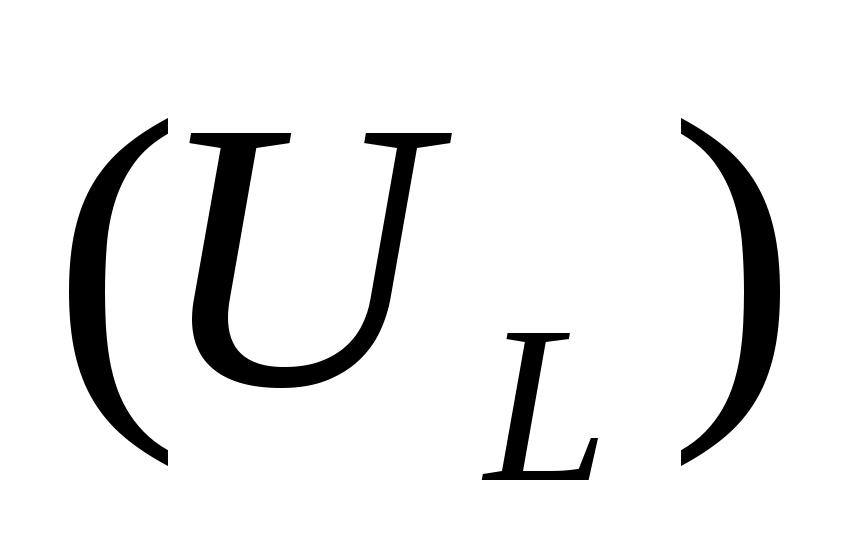 кернеулер амплитудалары тең фазалары қарама-қарсы болады, бұл құбылыс кернеулер резонансы ( тізбектелген резонанс ), ал
кернеулер амплитудалары тең фазалары қарама-қарсы болады, бұл құбылыс кернеулер резонансы ( тізбектелген резонанс ), ал
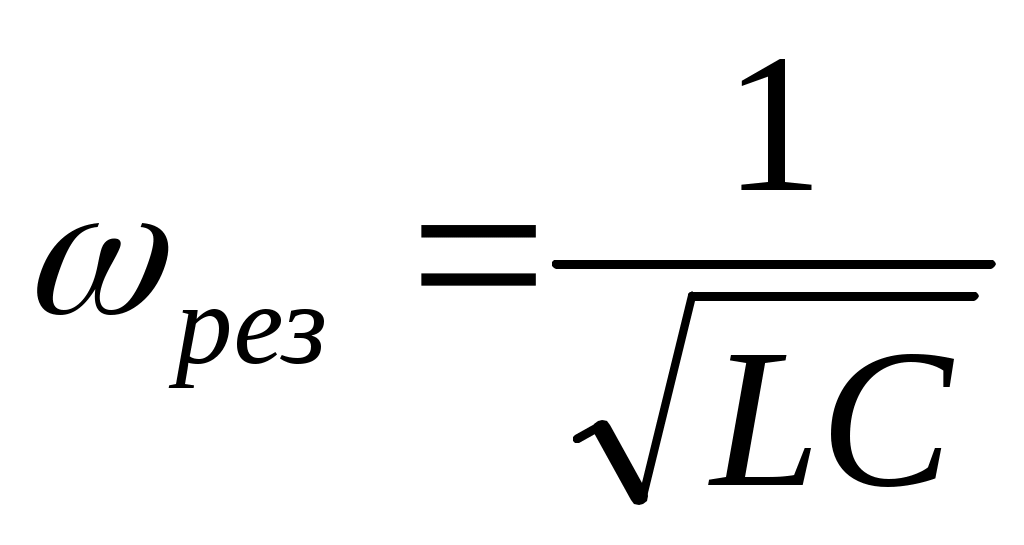 (11.23)
(11.23)
резонанс жиілігі деп аталады.
Егер параллель жалғанған конденсатор мен шарғыға түсіп тұрған кернеу жиілігі
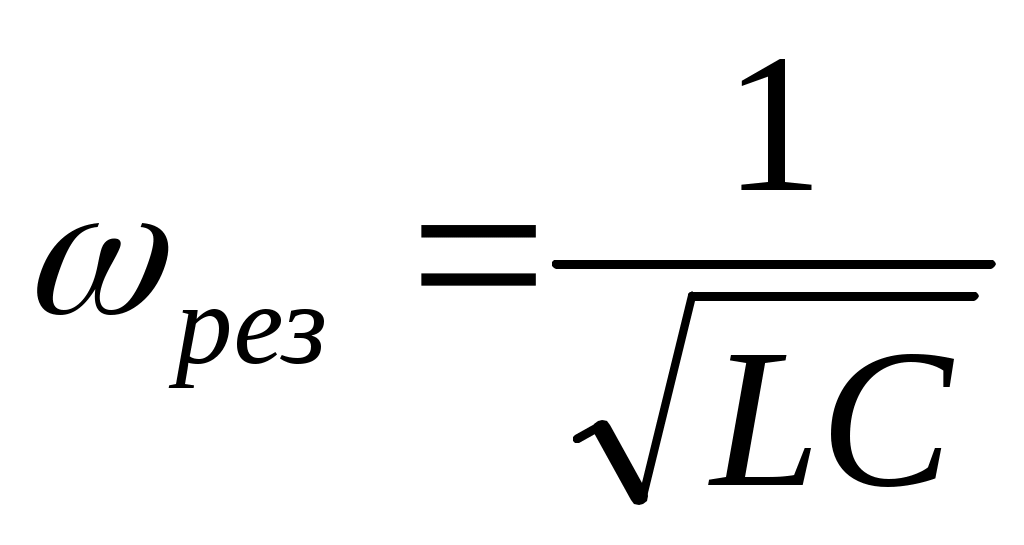 болса
болса
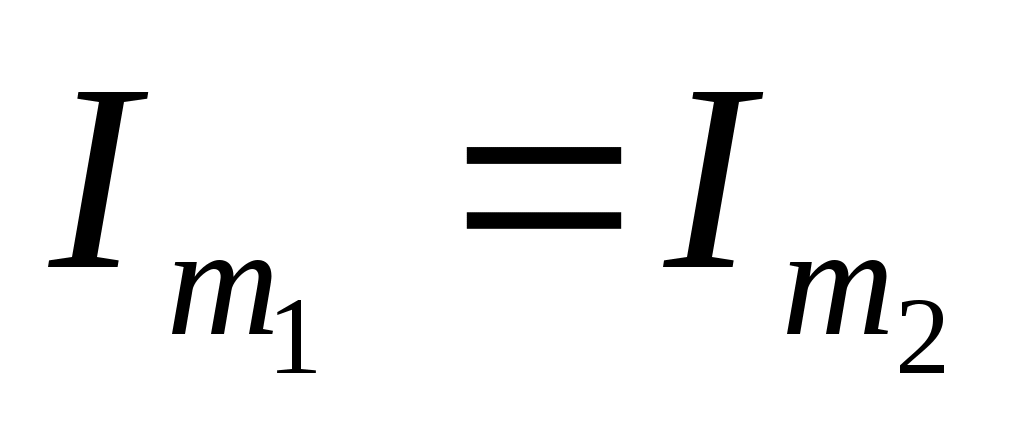 және
және 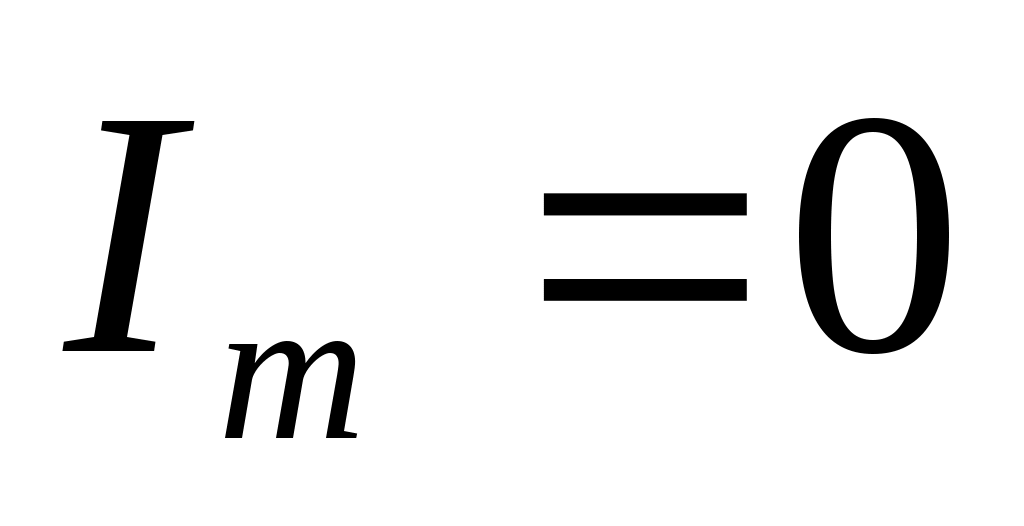 болады.
болады.
Бұл токтар резонансы параллель резонанс деп аталады.
Максвелл теңдеулерінен кеңістікте айнымалы электромагниттік өрістің шектеулі жылдамдықпен таралуы-электромагниттік толқынның таралуы келіп шығады. Электромагниттік толқын көзі кез келген электр тербелмелі контур немесе өткізгіш болуы мүмкін.
Максвелл теориясы бойынша электромагниттік толқынның көлденең толқын (  және
және 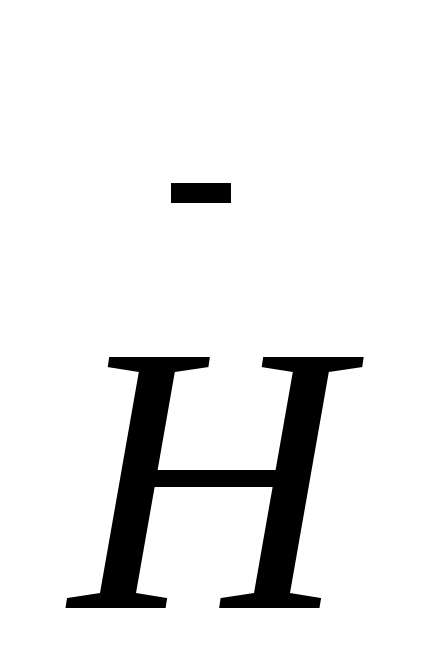 ) векторлары бір-біріне перпендикуляр және электромагниттік толқын таралу жылдамдығы
) векторлары бір-біріне перпендикуляр және электромагниттік толқын таралу жылдамдығы 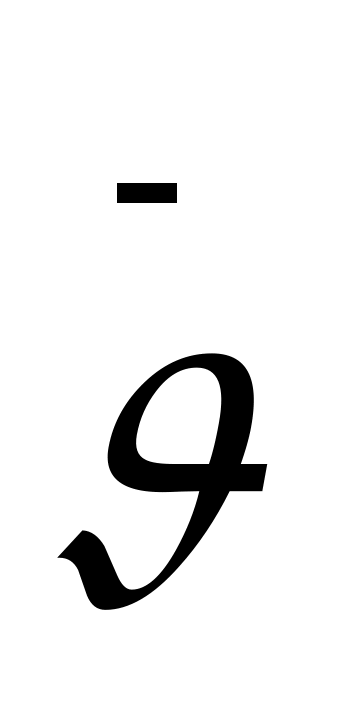 векторына перпендикуляр тегістікте жатады.
векторына перпендикуляр тегістікте жатады.  және
және 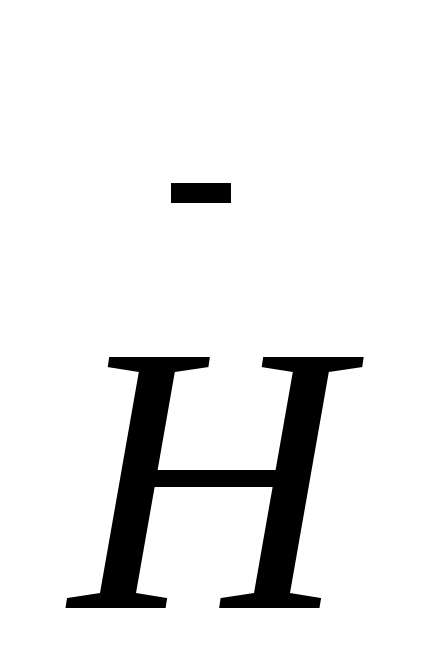 векторлары әр уақытта бір фазада тербеледі, олардың лездік мәндері кез келген нүктеде
векторлары әр уақытта бір фазада тербеледі, олардың лездік мәндері кез келген нүктеде
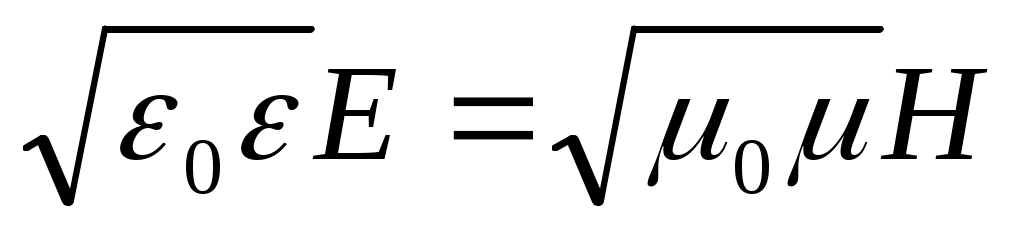 (11.24)
(11.24)
Электромагниттік толқын энергиясының көлемдік тығыздығы
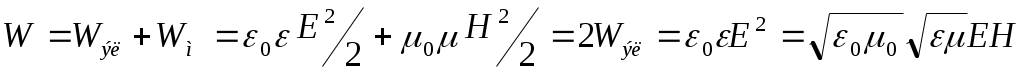 (11.25)
(11.25)
Электромагниттік толқынның фазалық жылдамдығы
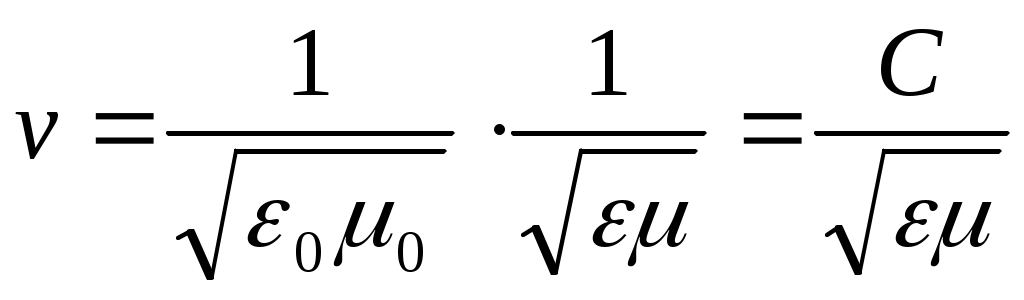 (11.26)
(11.26)
Бұлардың көбейтіндісі
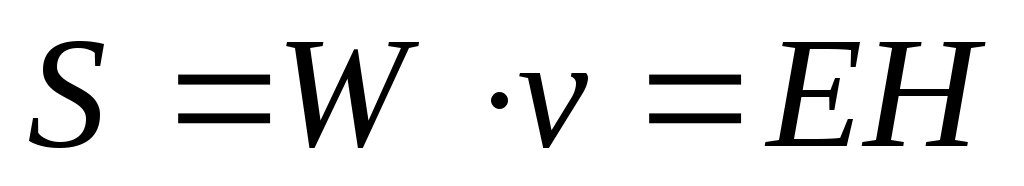 (11.27)
(11.27)
Электромагниттік энергия ағымының тығыздық векторы
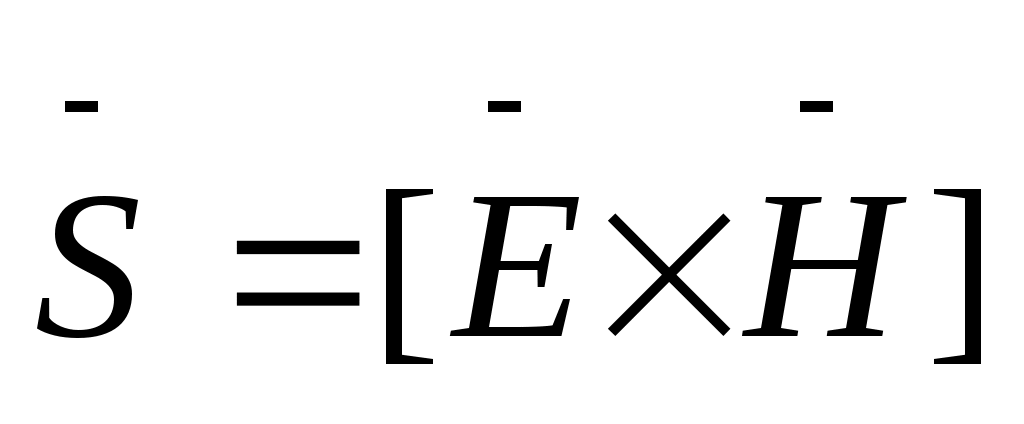 (11.28)
(11.28)
Умов-Пойнтинг векторы деп аталады.
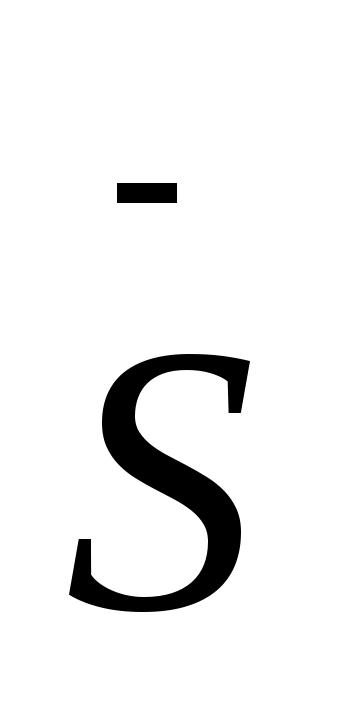 векторы электромагниттік толқын таралу бағытымен бірдей, оның модулі электромагниттік толқынның уақыт бірлігінде толқын таралу бағытына перпендикуляр жайласқан бірлік ауданшадан өткен энергияға тең.
векторы электромагниттік толқын таралу бағытымен бірдей, оның модулі электромагниттік толқынның уақыт бірлігінде толқын таралу бағытына перпендикуляр жайласқан бірлік ауданшадан өткен энергияға тең.
ЛЕКЦИЯ №12
Геометриялық оптика туралы түсінік.
Фотометрия. Жарық толқындарының қасиеттері.
-
Геометриялық оптиканың заңдары.
-
Оптикалық приборлар.
-
Фотометрия.
-
Жарық толқындарының интерференциясы. Интерферометрлер.
-
Толқын дифракциясы.
-
Голография.
Жарық табиғаты анықталмай тұрып-ақ оптиканың мынадай негізгі заңдары белгілі еді:
а) Жарықтың түзу сызық бойынша таралу заңы – жарық оптикалық біртекті ортада тұзу сызық бойынша таралады.
ә) Жарық шоқтарының тәуелсіздік заңы: бөлек жарық шоғының әсері онымен бір уақытта тағы да басқа бар ма, жоқ па оған байланысты емес.
в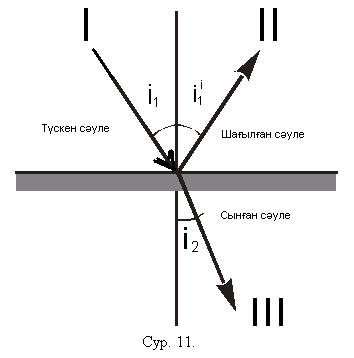 ) Шағылу заңы: қайтқан сәуле түскен сәулемен түсіп тұрған нүктеге қойылған перпендикуляр жататын тегістікте жатады, шағылу бұрышы түсу бұрышына тең.
) Шағылу заңы: қайтқан сәуле түскен сәулемен түсіп тұрған нүктеге қойылған перпендикуляр жататын тегістікте жатады, шағылу бұрышы түсу бұрышына тең.
г) Сыну заңы: түскен сәуле, сынған сәуле және түскен нүктеге қойылған перпендикуляр бір тегістікте жатады; түсу бұрышы синусының сыну бұрышының синусына қатынасы осы орталар үшін тұрақты шама болады:
sin i1 / sin i2 = n21 (12.1)
мұндағы n21 – ІІ ортаның І ортаға салыстырғандағы сыну көрсеткіші деп аталады, ол шама осы екі орталардың абсолют сыну көрсеткіштердің қатынас ына тең болады:
п21 = п2 /п1 (12.2)
Ортаның абсолют сыну көрсеткіші деп п = с/v (12.3) қатнасты айтады, бұл жердегі с – электромагниттік толқынның вакуумдегі жылдамдығы, v – осы ортадағы фазалық жылдамдығы.
(11.26) формуламен салыстырғанда
n=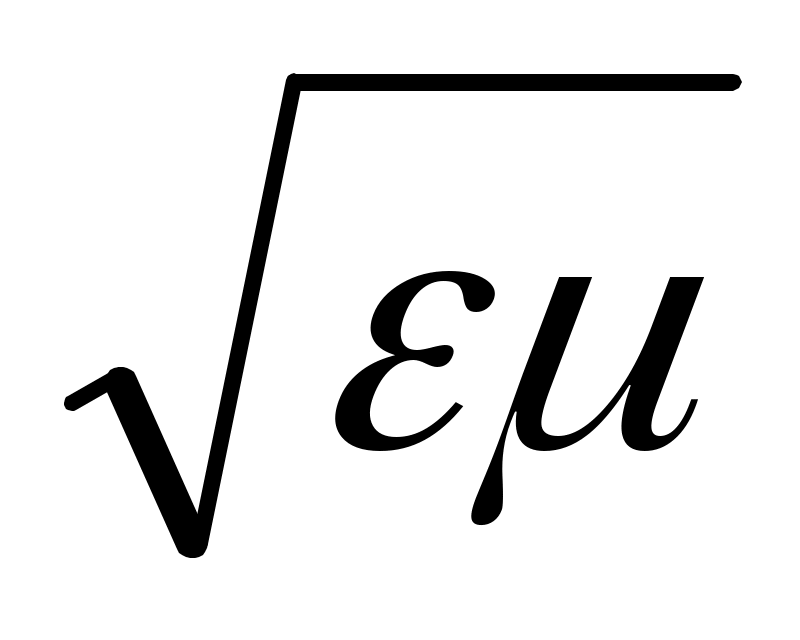 (12.4)
(12.4)
шығады, (12.2) формуласынан
n1sin i1=n2sin i2 (12.5)
шығады. (12.5) өрнектен жарық сәулелерінің қайтымдылығы келіп шығады.Егер жарық сыну көрсеткіші көбірек ортадан сыну көрсеткіші кемірек ортаға өтсе, онда 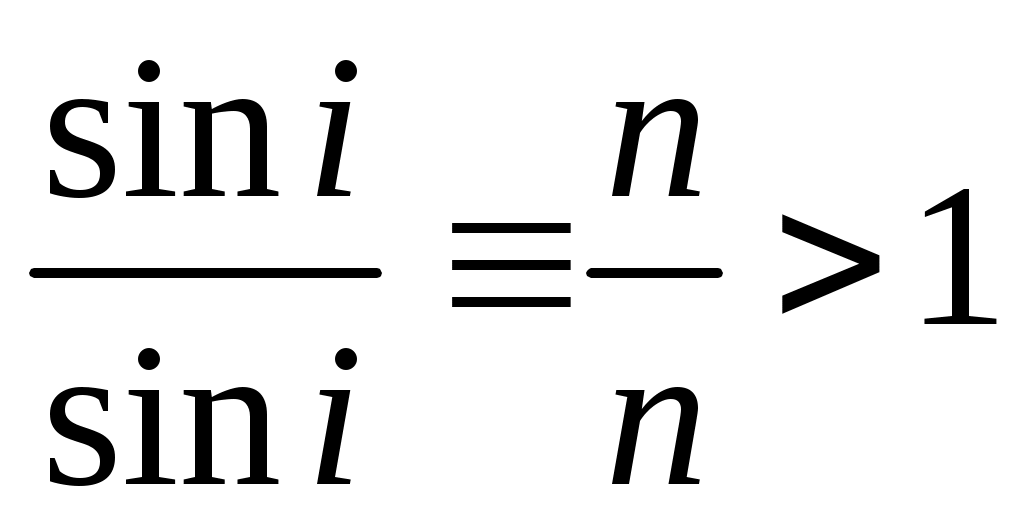

Сонда сынған нұр нормальдан алыстай түседі – сыну бұрышы (і2) түсу бұрышы- нан (і1) көбірек болады, түсу бұрышының бір шамасында (і1=ішек) сыну бұрышы π/2-ге тең болады, ішек – шекті бұрыш деп аталады. Түсу бұрышы і1> ішек болғанда жарық толығымен шағылып қайтады, бұл құбылыс толық ішке шағылу деп аталады. Сонда
sin ішек = п2/п1 = п21 (12.6).
п2 ≤ п1 шарты орындалу керек.
Толық ішке шағылу құбылысы оптикалық аспаптарда: бинокльдерде, перископтарда және т.б. кеңінен қолданылады.
Жарық таралу заңдылықтары жарық сәулелері түсінігіне негізделген оптиканың бөлімін геометриялық оптика деп аталады. Екі беттерімен шектелген мөлдір денелерді линза деп атайды. Оптикалық қасиеттері бойынша линзалар жинаушы және шашыратушы болып бөлінеді.
Ферма принципі (немесе ең аз уақыт принципі) – жарық әрқашан осы таралуға кез келген басқа жолдардың ішінен ең аз уақыт кететін жолмен таралады.
Линза формуласы бойынша:
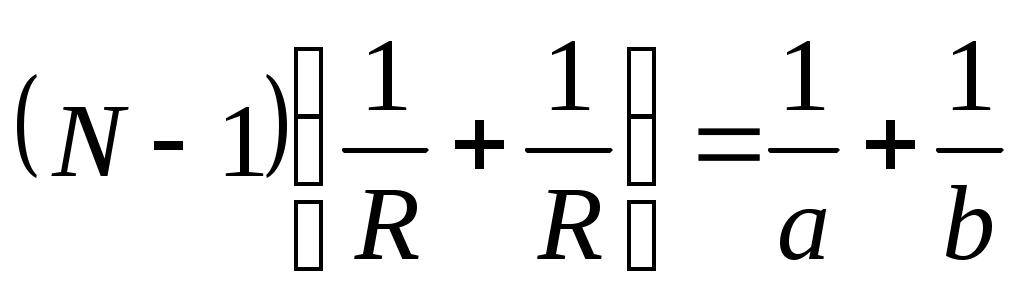
 (12.7)
(12.7)
Мұндағы N=n/n1 (n,n1 – линза мен қоршаған орта абсолют сындыру көрсеткіштері).
Е гер а ∞ (сәулелер параллель шоқ бойынша түсіп отыр) онда
гер а ∞ (сәулелер параллель шоқ бойынша түсіп отыр) онда 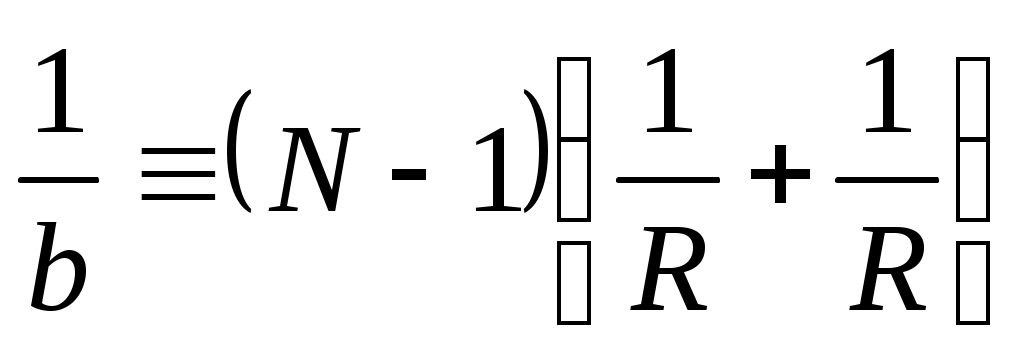 , осыған сәйкес
, осыған сәйкес
қашықтық b=OF=ƒ линзаның фокустық қашықтығы деп аталады.
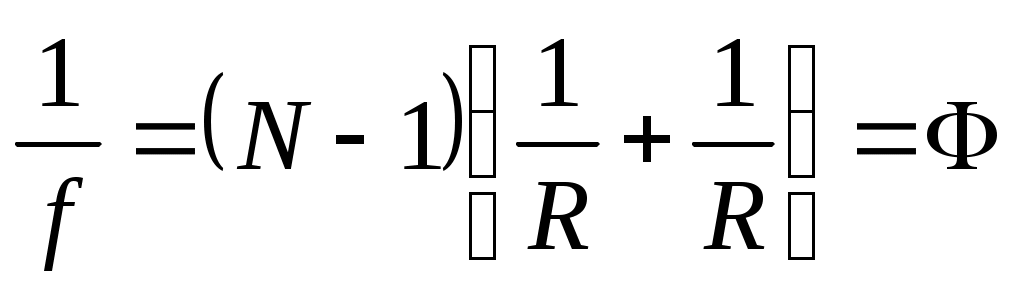 (12.8)
(12.8)
шама линзаның оптикалық күші деп аталады. Линза формуласын
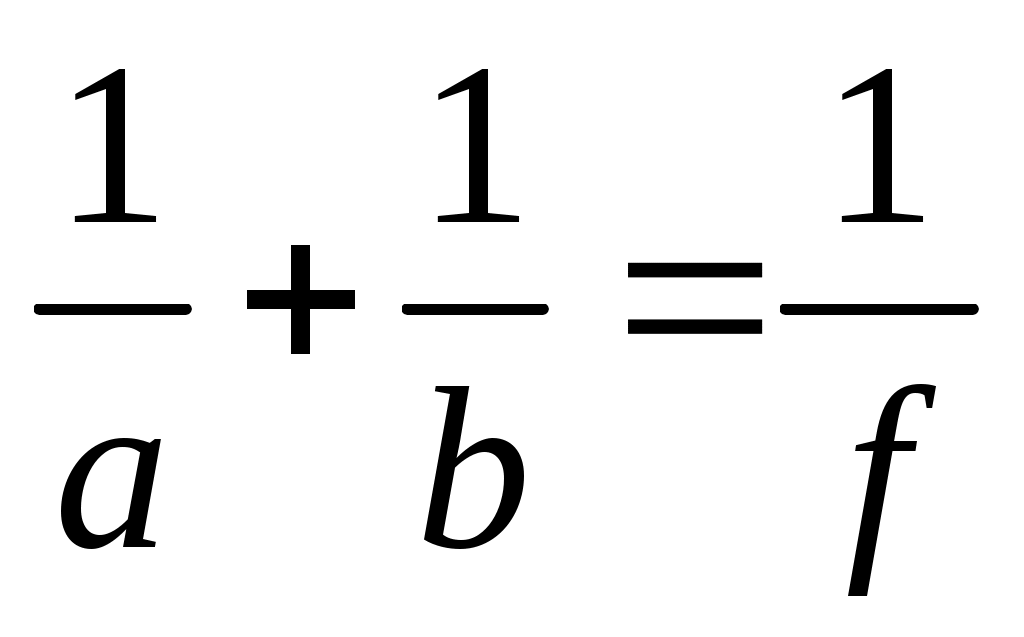 (12.9)
(12.9)
түрінде жазуға да болады. Шашыратушы линза үшін b мен f теріс деп алу керек.
Дененің кескінін линзаға салғанда мынадай сәулелер көмегімен салу керек:
-
Линзаның оптикалық осі арқылы өтетін сәуле таралу бағытын өзгертпейді.
-
Бас оптикалық оське параллель жүрген сәуле линзада сынғаннан кейін линзаның ІІ фокусы арқылы өтеді.
-
Линзаның І фокусы арқылы өткен сәуле линзада сынғаннан кейін оның бас оптикалық осіне параллель таралады.
Жарық және оның көздерінің интенсивтіліктерін зерттейтін оптиканың бөлімін фотометрия деп атайды.
БХЖ-да негізгі жарық өлшем бірлігі жарық күші -кандела.
Жарық ағыны Ф = J · Ω (11.10)
Өлшем бірлігі 1 люмен (лм) = 1лм = 1кд · 1ср
Жарық күші 1кд болған нүктелі жарық көзінің 1стерадиан (ср) денелік бұрышқа шығарып тұрған жарық ағыны. Жарқырау
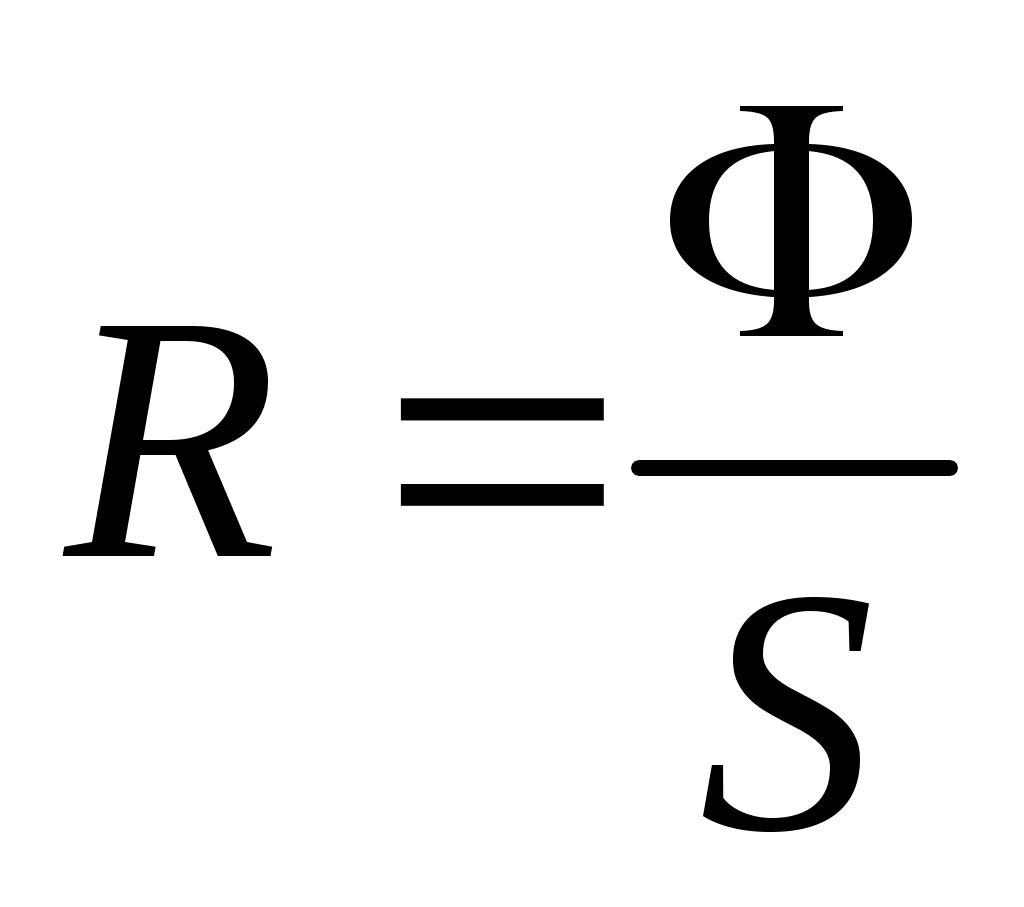 (12.11)
(12.11)
өрнекпен анықталады, өлшем бірлігі лм/м².
Жарықтылық
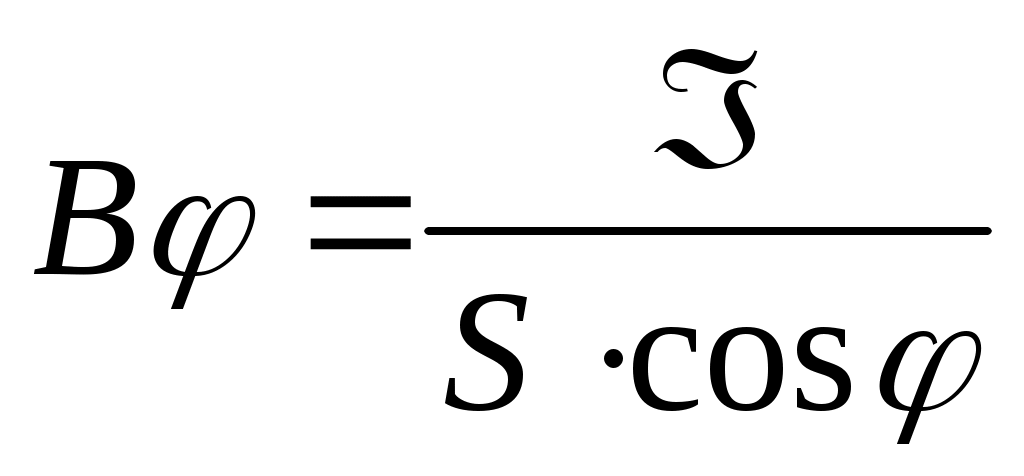 (12.12)
(12.12)
өлшем бірлігі кд/м².
Жарықталу – бетке түсіп тұрған жарық ағынының осы бет ауданына қатынасы:
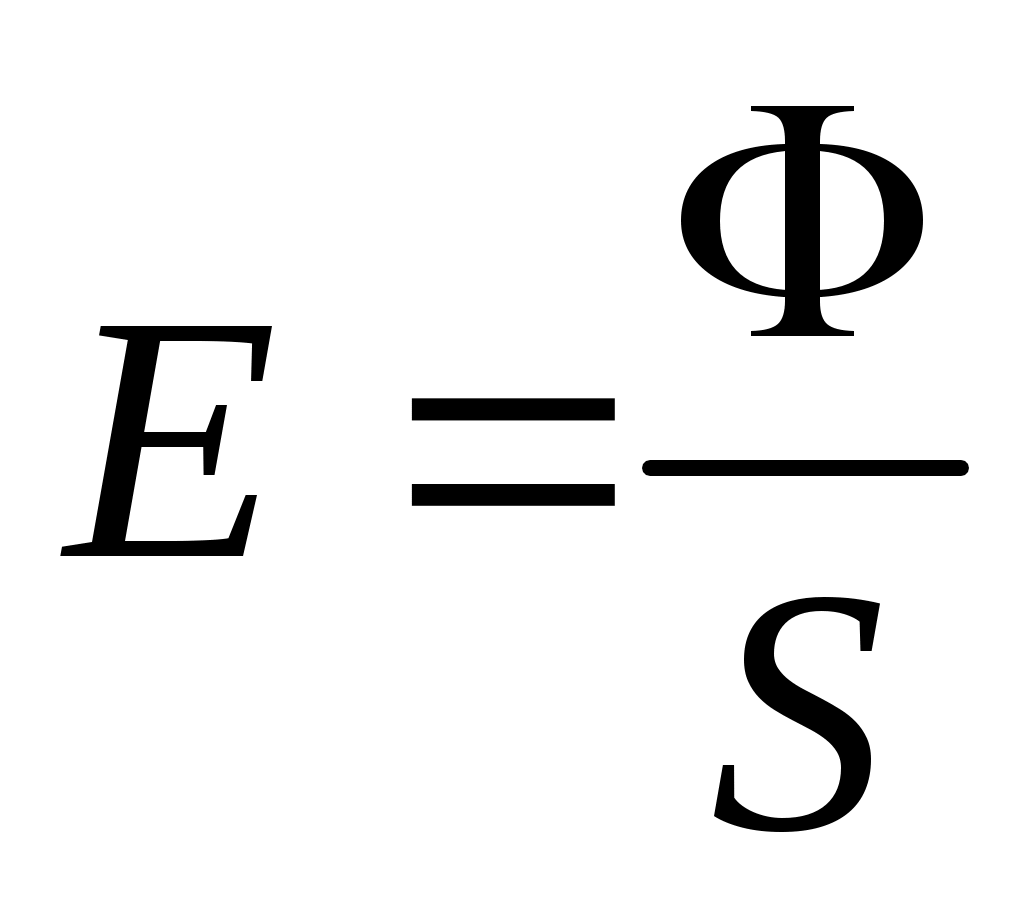 (12.13)
(12.13)
өлшем бірлігі люкс (лк) (1лк=1лм/ м²)
ХVII ғасырда жарықтың екі теориясы пайда болды: корпускулалық (Ньютон) және толқындық. Корпускулалық теория бойынша жарық жарқыраушы денелерден шығатын тік сызықты траекториялармен ұшушы бөлшектер (корпускулалар) ағымы. Жарық корпускулаларының қозғалысын Ньютон өзі тұжырымдаған механика заңдары бойынша қозғалуы керек. Бұл теория сол заманның өзінде біраз оптикалық құбылыстарды дұрыс түсіндіре алмады.
Толқындық теория бойынша жарық ерекше ортада - эфирде таралатын серпімді толқын. Эфир барлық әлем кеңістігін толтырады, барлық денелердің ішінде және механикалық қасиеттерге – серпімділік пен тығыздыққа ие. Толқындық теория Гюйгенс принципіне негізделген: толқын жеткен әрбір нүкте екінші толқынның центрі, ал сол толқындар сырты келесі мерзімдегі толқын шебі болып табылады.
Жарық толқындары бір-бірінен тәуелсіз таралып толқын суперпозиция (қабаттасу) принципі орындалады. Осы приципке негізделіп кез-келген синусоидалық емес толқынды оған эквивалент болған синусоидалық толқын жүйесі деп қарастыруға болады, демек толқын тобы немесе толқындық пакет түрінде көрсетуге болады. Қарапайым толқын тобы деп екі амплитудалары тең, жиіліктері жақын болған толқындар қосылғанда пайда болатын квазисинусоидалық жазық толқынды қарастыруға болады.
S=Aosin( t–kx)+Aosin[(
t–kx)+Aosin[( +d
+d )t–(k+dx)x]=2Aocos [(td
)t–(k+dx)x]=2Aocos [(td –kdk V2 sin (
–kdk V2 sin ( t–k)] (12.14).
t–k)] (12.14).
Оның таралу жылдамдығы деп осы толқындағы белгілі бір нүктенің орын ауыстыру жылдамдығын алады, ондағы амплитуда белгілі бір тұрақты шама болады. Демек
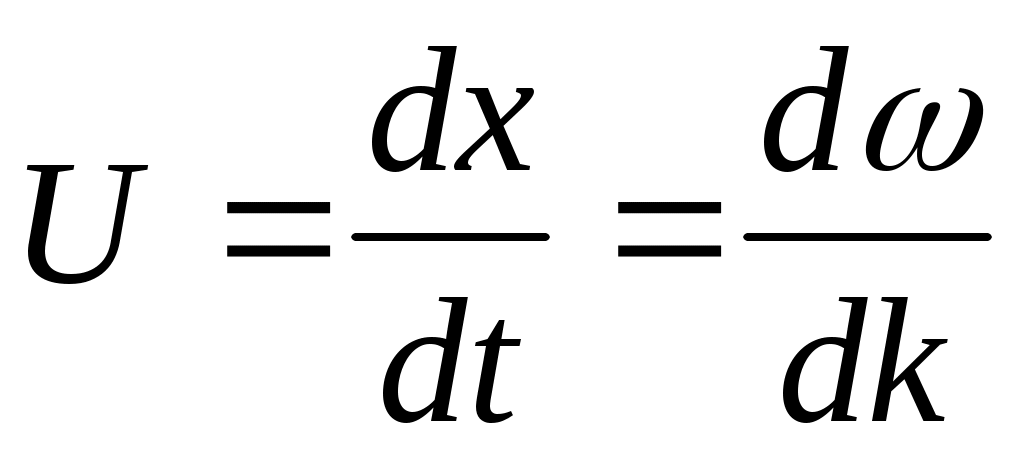 (12.15)
(12.15)
Осы шаманы толқынның топтық жылдамдығы деп атайды. Екі монохроматты жарық толқындары түйіскенде кеңістіктің белгілі бір нүктесінде бір бағыттағы тербелістерді қоздырады.
Х1 = A1cos ( t + φ1) және X2 = A2cos (
t + φ1) және X2 = A2cos ( t + φ2) (12.16)
t + φ2) (12.16)
Мұндағы Х1, Х2 деп толқындағы электр және магнит өрістерінің кернеулік векторлары. Нәтижелеуші тербеліс амплитудасы.
А² = A1² + A2² + 2A1A2 cos (φ2 – φ1) (12.17)
Егер екі толқын фазалар айырмасы уақытқа тәуелді болмай тұрақты болып қалатын болса ондай толқындарды когерентті дейді. Когерентті толқындар үшін cos(φ2 – φ1) шамасы тұрақты болады. Нәтижелеуші толқын интенсивтілігі (І А²) кеңістіктің cos(φ2 – φ1) > 0 болған нүктелерінде І > I1 + I2, ал cos(φ2 – φ1) < 0 болған нүктелерінде І < I1 + I2 , болады. Демек екі (немесе бірнеше) когерентті жарық толқындар түйіскенде кеңістіктің бір нүктелерінде интенсивтіліктің max, екінші бір нүктелерінде min пайда болады. Бұл құбылыс жарық интерференциясы деп аталады.
Толқындар интерференциясы болуы үшін түйісуші толқындар когерентті (толқындардың фазалық айырымы уақыт бойынша тұрақты)және монохроматты(тек жалғыз толқын ұзындығы болу) болуы керек.
1 2 3 4 5 6 7 8
Тербелмелі контур.
Айнымалы электр тоғы.
Кернеулер және токтар резонансы.
Электромагниттік өріс үшін толқындық теңдеу.
Электромагниттік энергияның ток тығыздығы.
Геометриялық оптиканың заңдары.
Оптикалық приборлар.
Фотометрия.
Жарық толқындарының интерференциясы. Интерферометрлер.
Толқын дифракциясы.
Голография.
в
 ) Шағылу заңы: қайтқан сәуле түскен сәулемен түсіп тұрған нүктеге қойылған перпендикуляр жататын тегістікте жатады, шағылу бұрышы түсу бұрышына тең.
) Шағылу заңы: қайтқан сәуле түскен сәулемен түсіп тұрған нүктеге қойылған перпендикуляр жататын тегістікте жатады, шағылу бұрышы түсу бұрышына тең.г) Сыну заңы: түскен сәуле, сынған сәуле және түскен нүктеге қойылған перпендикуляр бір тегістікте жатады; түсу бұрышы синусының сыну бұрышының синусына қатынасы осы орталар үшін тұрақты шама болады:
sin i1 / sin i2 = n21 (12.1)
мұндағы n21 – ІІ ортаның І ортаға салыстырғандағы сыну көрсеткіші деп аталады, ол шама осы екі орталардың абсолют сыну көрсеткіштердің қатынас ына тең болады:
п21 = п2 /п1 (12.2)
Ортаның абсолют сыну көрсеткіші деп п = с/v (12.3) қатнасты айтады, бұл жердегі с – электромагниттік толқынның вакуумдегі жылдамдығы, v – осы ортадағы фазалық жылдамдығы.
(11.26) формуламен салыстырғанда
n=
шығады, (12.2) формуласынан
n1sin i1=n2sin i2 (12.5)
шығады. (12.5) өрнектен жарық сәулелерінің қайтымдылығы келіп шығады.Егер жарық сыну көрсеткіші көбірек ортадан сыну көрсеткіші кемірек ортаға өтсе, онда
Сонда сынған нұр нормальдан алыстай түседі – сыну бұрышы (і2) түсу бұрышы- нан (і1) көбірек болады, түсу бұрышының бір шамасында (і1=ішек) сыну бұрышы π/2-ге тең болады, ішек – шекті бұрыш деп аталады. Түсу бұрышы і1> ішек болғанда жарық толығымен шағылып қайтады, бұл құбылыс толық ішке шағылу деп аталады. Сонда
sin ішек = п2/п1 = п21 (12.6).
п2 ≤ п1 шарты орындалу керек.
Толық ішке шағылу құбылысы оптикалық аспаптарда: бинокльдерде, перископтарда және т.б. кеңінен қолданылады.
Жарық таралу заңдылықтары жарық сәулелері түсінігіне негізделген оптиканың бөлімін геометриялық оптика деп аталады. Екі беттерімен шектелген мөлдір денелерді линза деп атайды. Оптикалық қасиеттері бойынша линзалар жинаушы және шашыратушы болып бөлінеді.
Ферма принципі (немесе ең аз уақыт принципі) – жарық әрқашан осы таралуға кез келген басқа жолдардың ішінен ең аз уақыт кететін жолмен таралады.
Линза формуласы бойынша:
Мұндағы N=n/n1 (n,n1 – линза мен қоршаған орта абсолют сындыру көрсеткіштері).
Е
 гер а ∞ (сәулелер параллель шоқ бойынша түсіп отыр) онда
гер а ∞ (сәулелер параллель шоқ бойынша түсіп отыр) онда қашықтық b=OF=ƒ линзаның фокустық қашықтығы деп аталады.
шама линзаның оптикалық күші деп аталады. Линза формуласын
түрінде жазуға да болады. Шашыратушы линза үшін b мен f теріс деп алу керек.
Дененің кескінін линзаға салғанда мынадай сәулелер көмегімен салу керек:
-
Линзаның оптикалық осі арқылы өтетін сәуле таралу бағытын өзгертпейді. -
Бас оптикалық оське параллель жүрген сәуле линзада сынғаннан кейін линзаның ІІ фокусы арқылы өтеді. -
Линзаның І фокусы арқылы өткен сәуле линзада сынғаннан кейін оның бас оптикалық осіне параллель таралады.
Жарық және оның көздерінің интенсивтіліктерін зерттейтін оптиканың бөлімін фотометрия деп атайды.
БХЖ-да негізгі жарық өлшем бірлігі жарық күші -кандела.
Жарық ағыны Ф = J · Ω (11.10)
Өлшем бірлігі 1 люмен (лм) = 1лм = 1кд · 1ср
Жарық күші 1кд болған нүктелі жарық көзінің 1стерадиан (ср) денелік бұрышқа шығарып тұрған жарық ағыны. Жарқырау
өрнекпен анықталады, өлшем бірлігі лм/м².
Жарықтылық
өлшем бірлігі кд/м².
Жарықталу – бетке түсіп тұрған жарық ағынының осы бет ауданына қатынасы:
өлшем бірлігі люкс (лк) (1лк=1лм/ м²)
ХVII ғасырда жарықтың екі теориясы пайда болды: корпускулалық (Ньютон) және толқындық. Корпускулалық теория бойынша жарық жарқыраушы денелерден шығатын тік сызықты траекториялармен ұшушы бөлшектер (корпускулалар) ағымы. Жарық корпускулаларының қозғалысын Ньютон өзі тұжырымдаған механика заңдары бойынша қозғалуы керек. Бұл теория сол заманның өзінде біраз оптикалық құбылыстарды дұрыс түсіндіре алмады.
Толқындық теория бойынша жарық ерекше ортада - эфирде таралатын серпімді толқын. Эфир барлық әлем кеңістігін толтырады, барлық денелердің ішінде және механикалық қасиеттерге – серпімділік пен тығыздыққа ие. Толқындық теория Гюйгенс принципіне негізделген: толқын жеткен әрбір нүкте екінші толқынның центрі, ал сол толқындар сырты келесі мерзімдегі толқын шебі болып табылады.
Жарық толқындары бір-бірінен тәуелсіз таралып толқын суперпозиция (қабаттасу) принципі орындалады. Осы приципке негізделіп кез-келген синусоидалық емес толқынды оған эквивалент болған синусоидалық толқын жүйесі деп қарастыруға болады, демек толқын тобы немесе толқындық пакет түрінде көрсетуге болады. Қарапайым толқын тобы деп екі амплитудалары тең, жиіліктері жақын болған толқындар қосылғанда пайда болатын квазисинусоидалық жазық толқынды қарастыруға болады.
S=Aosin(
Оның таралу жылдамдығы деп осы толқындағы белгілі бір нүктенің орын ауыстыру жылдамдығын алады, ондағы амплитуда белгілі бір тұрақты шама болады. Демек
Осы шаманы толқынның топтық жылдамдығы деп атайды. Екі монохроматты жарық толқындары түйіскенде кеңістіктің белгілі бір нүктесінде бір бағыттағы тербелістерді қоздырады.
Х1 = A1cos (
Мұндағы Х1, Х2 деп толқындағы электр және магнит өрістерінің кернеулік векторлары. Нәтижелеуші тербеліс амплитудасы.
А² = A1² + A2² + 2A1A2 cos (φ2 – φ1) (12.17)
Егер екі толқын фазалар айырмасы уақытқа тәуелді болмай тұрақты болып қалатын болса ондай толқындарды когерентті дейді. Когерентті толқындар үшін cos(φ2 – φ1) шамасы тұрақты болады. Нәтижелеуші толқын интенсивтілігі (І А²) кеңістіктің cos(φ2 – φ1) > 0 болған нүктелерінде І > I1 + I2, ал cos(φ2 – φ1) < 0 болған нүктелерінде І < I1 + I2 , болады. Демек екі (немесе бірнеше) когерентті жарық толқындар түйіскенде кеңістіктің бір нүктелерінде интенсивтіліктің max, екінші бір нүктелерінде min пайда болады. Бұл құбылыс жарық интерференциясы деп аталады.
Толқындар интерференциясы болуы үшін түйісуші толқындар когерентті (толқындардың фазалық айырымы уақыт бойынша тұрақты)және монохроматты(тек жалғыз толқын ұзындығы болу) болуы керек.
Когеренттік толқындар үшін cos(φ2 – φ1) = 1 болғанда max болатын нүктелерде І=4І, (І1=І2 болса), ал cos(φ2 – φ1) = -1 болатын нүктелерге min → І = 0 болады. Когеренттік емес толқындар үшін (φ2 – φ1) шамасы үздіксіз өзгеріп тұрады, сондықтан cos(φ2 – φ1) орташа мәні 0-ге тең болып барлық нүктелерде І=2І, (І1=І2). Когеренттік жарық толқындарын алу үшін бір толқын көзінен шыққан толқынды екіге бөліп қайта оларды түйістіреді, сүйтіп интерференция көрінісін бақылауға болады. Сонда бақылап тұрған нүктегегі тербелістер фаза айырмасы
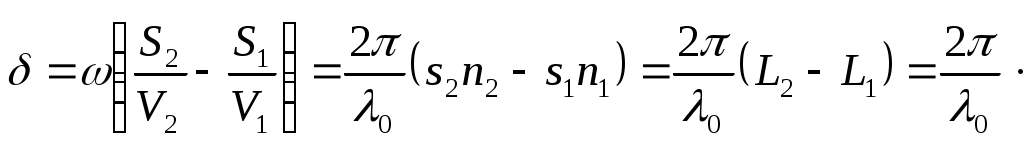 (12.18)
(12.18)
болады (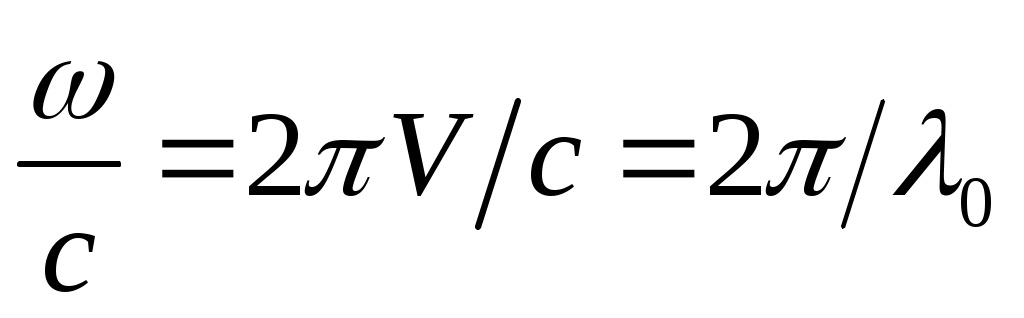 екенін ескердік,
екенін ескердік,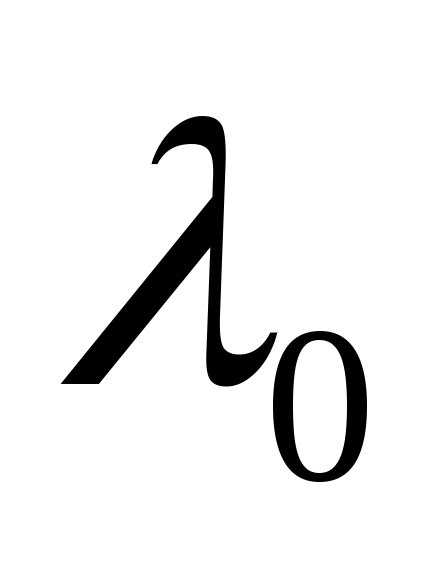 - вакуумдегі толқын ұзындығы), ▲= L2–L1 = S2n2 – S1n1 оптикалық жол айырымы деп аталады.
- вакуумдегі толқын ұзындығы), ▲= L2–L1 = S2n2 – S1n1 оптикалық жол айырымы деп аталады.
Егер оптикалық жол айырымы вакуумдегі толқын ұзындықтарының бүтін санына тең болса
▲= ± m λ0 (m = 0, 1, 2, ...) (12.19)
онда ▲= ± 2mπ болып осы нүктеде қозған екі толқын да бір фазада болып бір-бірін күшейтеді, бұл интерференция max шарты болып табылады. Егер де
▲= ± ( 2m + 1)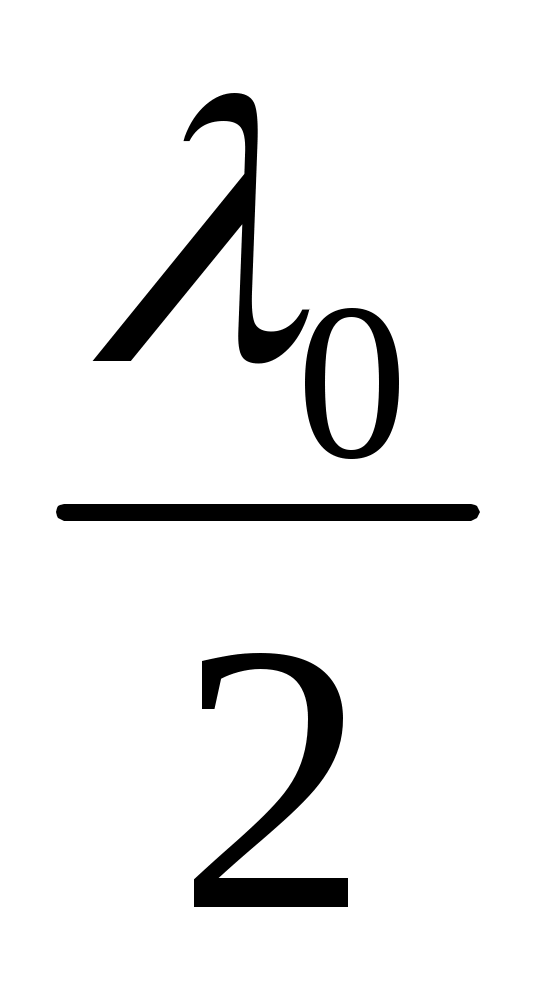 (m = 0, 1, 2, ...) (12.20)
(m = 0, 1, 2, ...) (12.20)
ол нүктедегі тербелістер қарама-қарсы фазада болады, тербелістер бір-бірін жояды, бұл интерференцияның минимум шарты болады.
Жарық интерференциясын жүзеге асыру үшін когерентті жарық шоқтары болу қажет, ол үшін әртүрлі әдістер пайдаланады. Лазерлер пайда болмастан бұрын бір көзден шыққан жарық шоқтарын бөліп кейін оларды қайтадан тоғыстыру нәтижесінде интерференцияны көру мүмкін еді.
Оған мысалдар: Юнг тәсілі, Френель бипризмасы мен айнасы және т.б.
Интерференция көкжиегінде интенсивтіліктің  максимумдері:
максимумдері:
Х max = ± 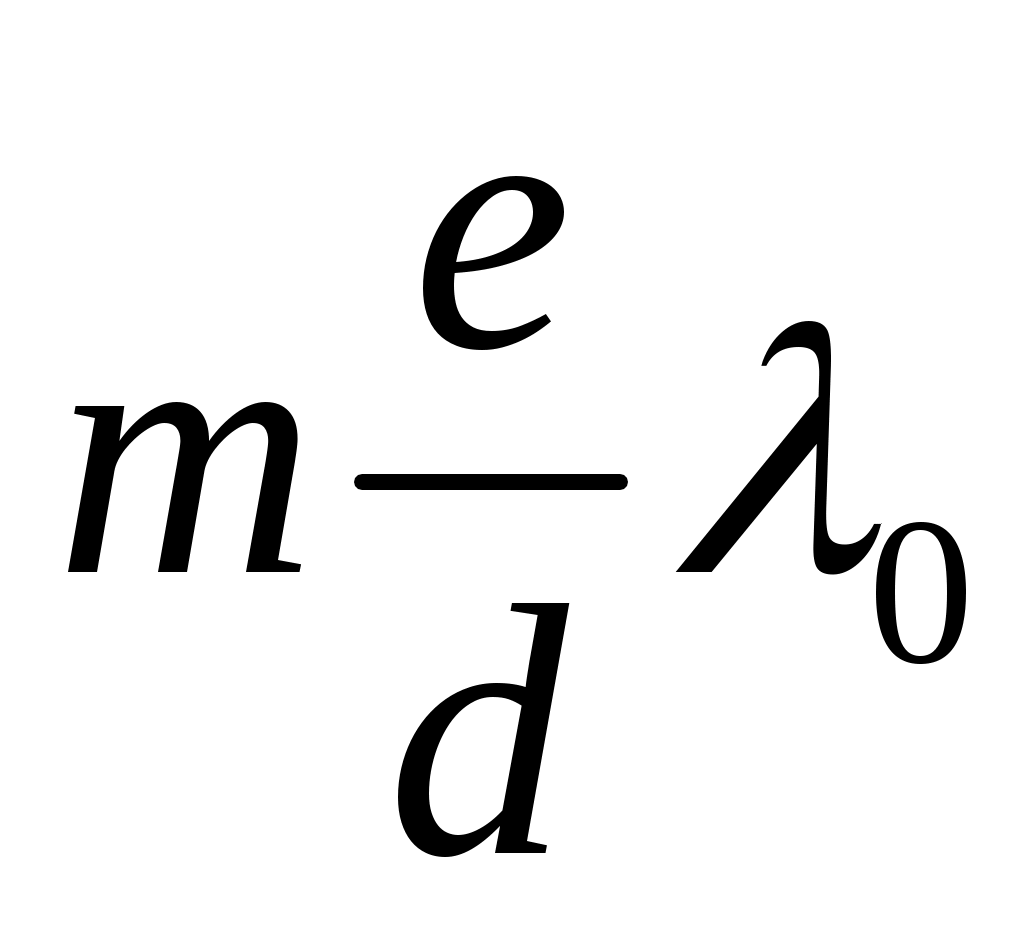 (m = 0, 1, 2, ...) (12.21)
(m = 0, 1, 2, ...) (12.21)
минимумдері:
Х min = ± 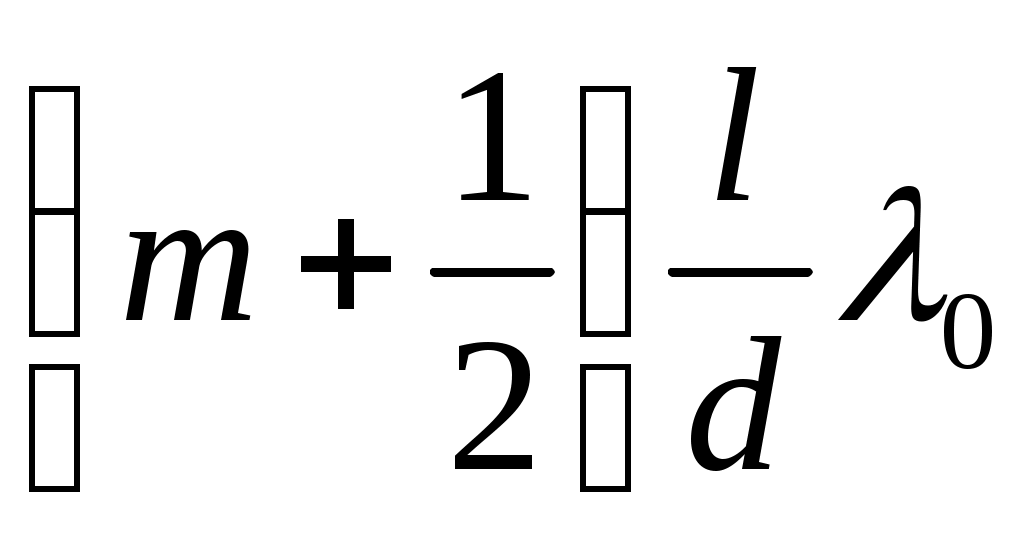 (m = 0, 1, 2, ...) (12.22)
(m = 0, 1, 2, ...) (12.22)
нүктелерінде көрінеді.
Ньютон сақиналары тең қалыңдық жолақтарына айқын мысал. Ондағы (шағылу жарық үшін) max шарты:
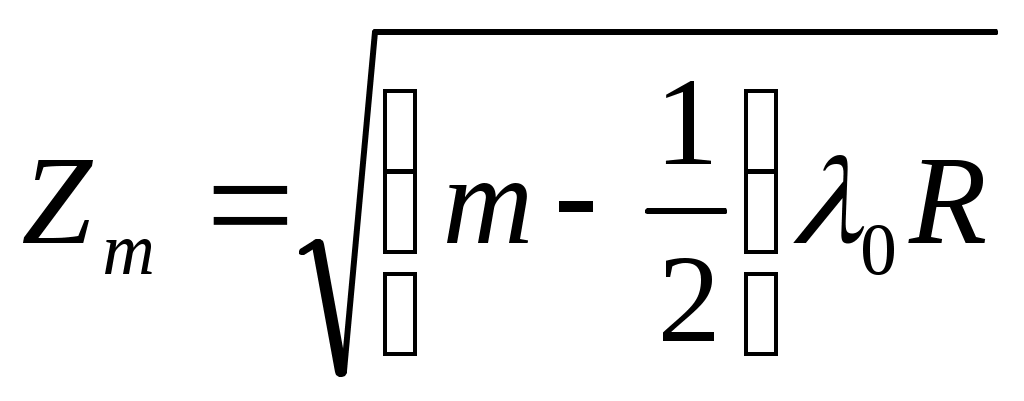 (m = 0, 1, 2, ...) (12.23)
(m = 0, 1, 2, ...) (12.23)
min шарты:
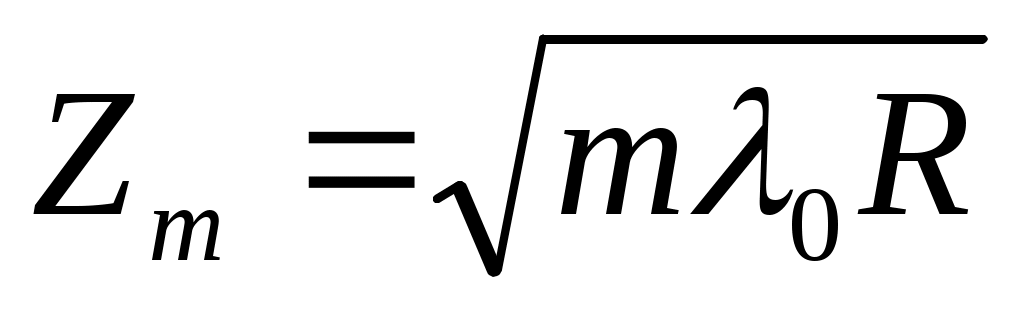 (m = 0, 1, 2, ...) (12.24)
(m = 0, 1, 2, ...) (12.24)
Өтуші жарық үшін max және min шарттары осы шарттардың орын ауыстыруы болады. Интерференция құбылысы интерферометр деп аталатын дәл өлшеуші аспаптарда пайдаланады.
Майкельсон интерферометрі жәрдемімен жоғары дәлдікпен (
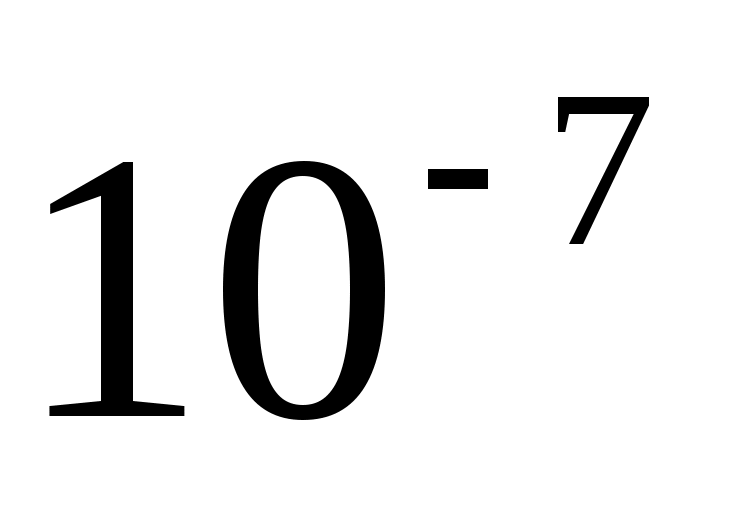 м) ұзындықтарды, температура өзгеруінде ұзындықтардың өзгеруін өлшеуге мүмкіншілік берді.
м) ұзындықтарды, температура өзгеруінде ұзындықтардың өзгеруін өлшеуге мүмкіншілік берді.
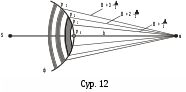 Гюйгенс-Френель принципі бойынша толқын көзі қоздырып тұрған толқынды жалған Ф жазықтығында жайласқан толқын көздері шығарып тұр деуге болады. Олар шығарған толқындар когерентті болады. Ол бетті сақина тәрізді зоналарға бөледі, көрші зоналарының шекарасынан М нүктесіне дейінгі қашықтықтар айырмасы λ/2 тең. Сонда әр зонадан шыққан тербелістер М нүктесінде қарама-қарсы фазада келеді, бір-бірін әлсіретеді. Сонда М нүктесіндегі нәтижелеуші жарық тербеліс амплитудасы
Гюйгенс-Френель принципі бойынша толқын көзі қоздырып тұрған толқынды жалған Ф жазықтығында жайласқан толқын көздері шығарып тұр деуге болады. Олар шығарған толқындар когерентті болады. Ол бетті сақина тәрізді зоналарға бөледі, көрші зоналарының шекарасынан М нүктесіне дейінгі қашықтықтар айырмасы λ/2 тең. Сонда әр зонадан шыққан тербелістер М нүктесінде қарама-қарсы фазада келеді, бір-бірін әлсіретеді. Сонда М нүктесіндегі нәтижелеуші жарық тербеліс амплитудасы
А = А1 – А2 + А3 – А4 + ... (12.25)
Френель зоналары ауданы
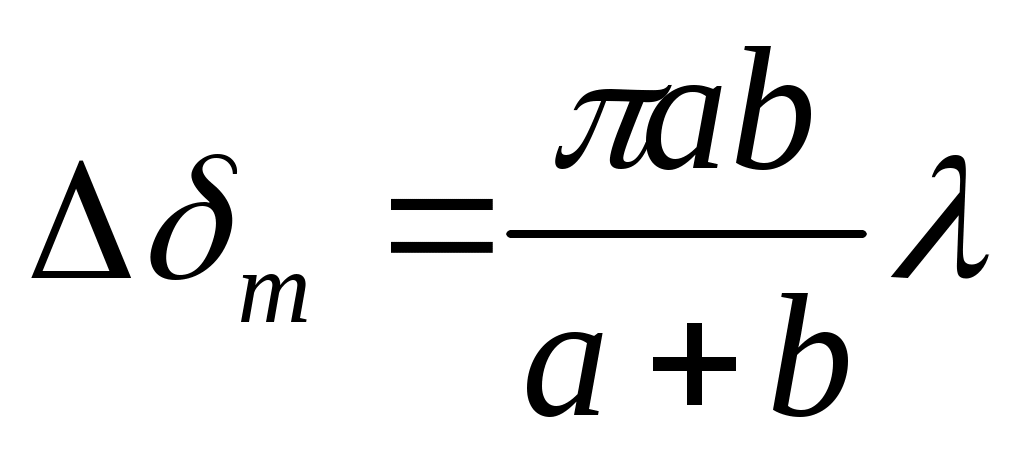 (12.26)
(12.26)
бұл өрнек т-ге тәуелді емес, тек a, b, λ мәндерімен анықталатын тұрақты шама. Сонда М нүктедегі тербеліс амплитудасы
А = А1 – А2 + А3 – А4 + ... =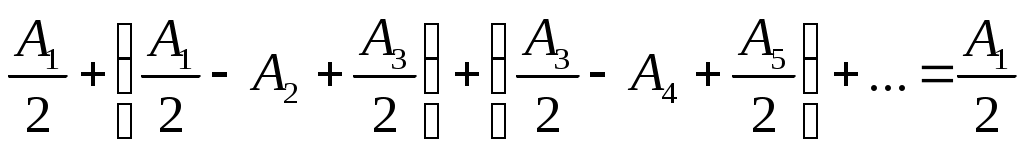 (12.27)
(12.27)
Мұндағы А1, А2, А3, ... -1, 2, 3, ... Френель зоналарының М нүктесінде қоздыратын тербелістер амплитудалары, жақша ішіндегі өрнектер 0-ге тең.
т-ші Френель зонасының радиусы
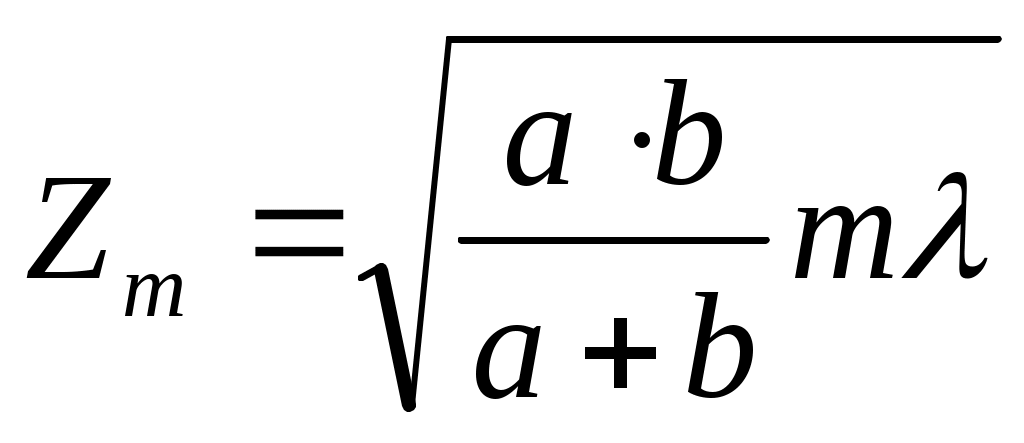 (12.28)
(12.28)
Т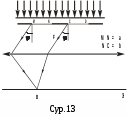 олқындардың жолдарындағы тосқауылдарды айналып өтуін немесе тосқауылға жақын жерлерде олардың таралуының геометриялық оптика заңдарынан ауытқуын дифракция деп атайды. Түйісетін сәулелер дифракциясын Френель дифракциясы дейді, оған мысалдар – дөңгелек тесіктердегі, дисктегі дифракция. Жазық толқындар немесе параллель сәулелер дифракциясын Фраунгофер дифракциясы дейді.
олқындардың жолдарындағы тосқауылдарды айналып өтуін немесе тосқауылға жақын жерлерде олардың таралуының геометриялық оптика заңдарынан ауытқуын дифракция деп атайды. Түйісетін сәулелер дифракциясын Френель дифракциясы дейді, оған мысалдар – дөңгелек тесіктердегі, дисктегі дифракция. Жазық толқындар немесе параллель сәулелер дифракциясын Фраунгофер дифракциясы дейді.  Ені а болған саңлауға параллель сәулелер шоғы түсіп тұрса Э экранға жететін жарық қалай үлесетінін Френель зоналар әдісін пайдаланып табуға болады. Дифракциялық минимум шарты
Ені а болған саңлауға параллель сәулелер шоғы түсіп тұрса Э экранға жететін жарық қалай үлесетінін Френель зоналар әдісін пайдаланып табуға болады. Дифракциялық минимум шарты
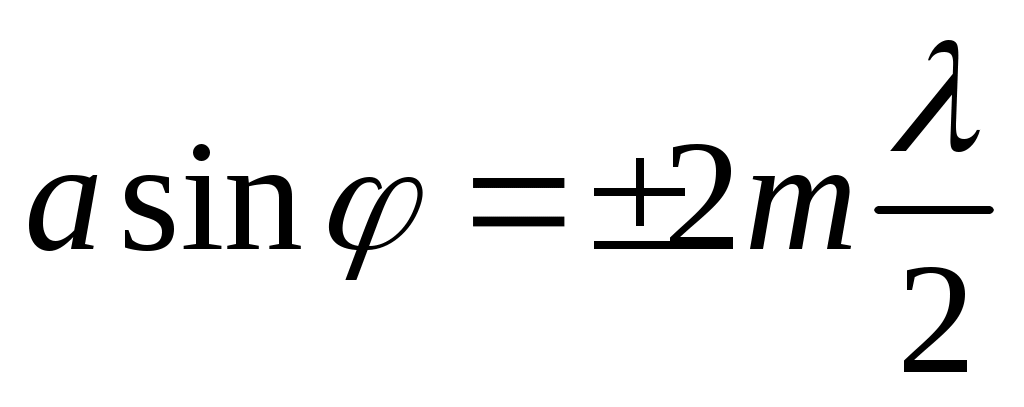 (т = 1, 2, 3, ...) (12.29)
(т = 1, 2, 3, ...) (12.29)
ал максимум шарты Во нүктесінде орталық дифракциялық максимум.
жайласқан, олардың арасындағы b аралықтан жарық қосымша минимумдер шарты
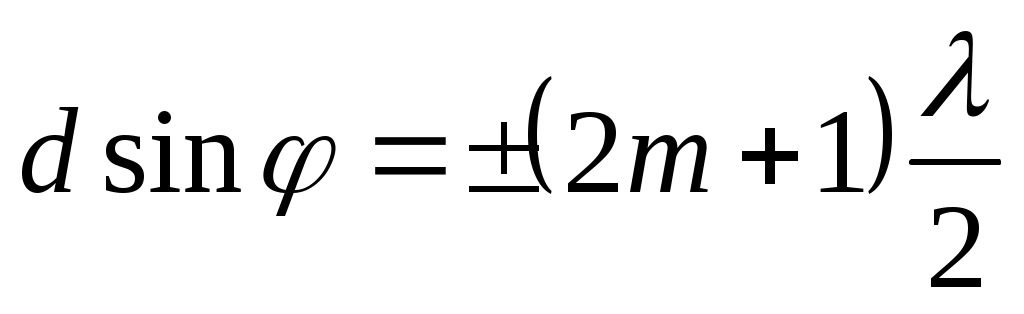 (т = 1, 2, 3, ...) (12.30).
(т = 1, 2, 3, ...) (12.30).
Дифракциялық тордағы басты максимумдер шарты
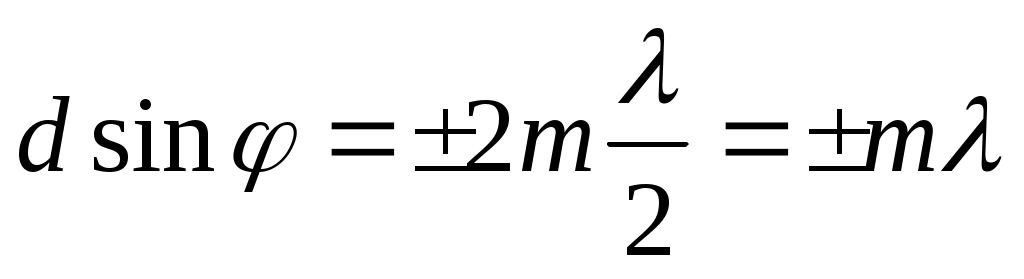 (т = 1, 2, 3, ...) (12.31)
(т = 1, 2, 3, ...) (12.31)
Спектрге жіктеу кеңінен спектрлік талдауда қолданылады.
ЛЕКЦИЯ №13
Заттағы электромагниттік тербеліс. Сәуленің кванттық табиғаты.
-
Жарықтың затта таралуы.
-
Жылулық сәулелену.
-
Абсолют қара дененің сәуле шығару қабілеті.
-
Кванттық гипотеза және Планк формуласы. Фотондар.
-
Фотоэффект.
-
Комптон эффектісі.
Заттың сыну көрсеткішінің жарық жиілігіне (толқын ұзындығына) байланыстылығы жарық дисперсиясы деп аталады.
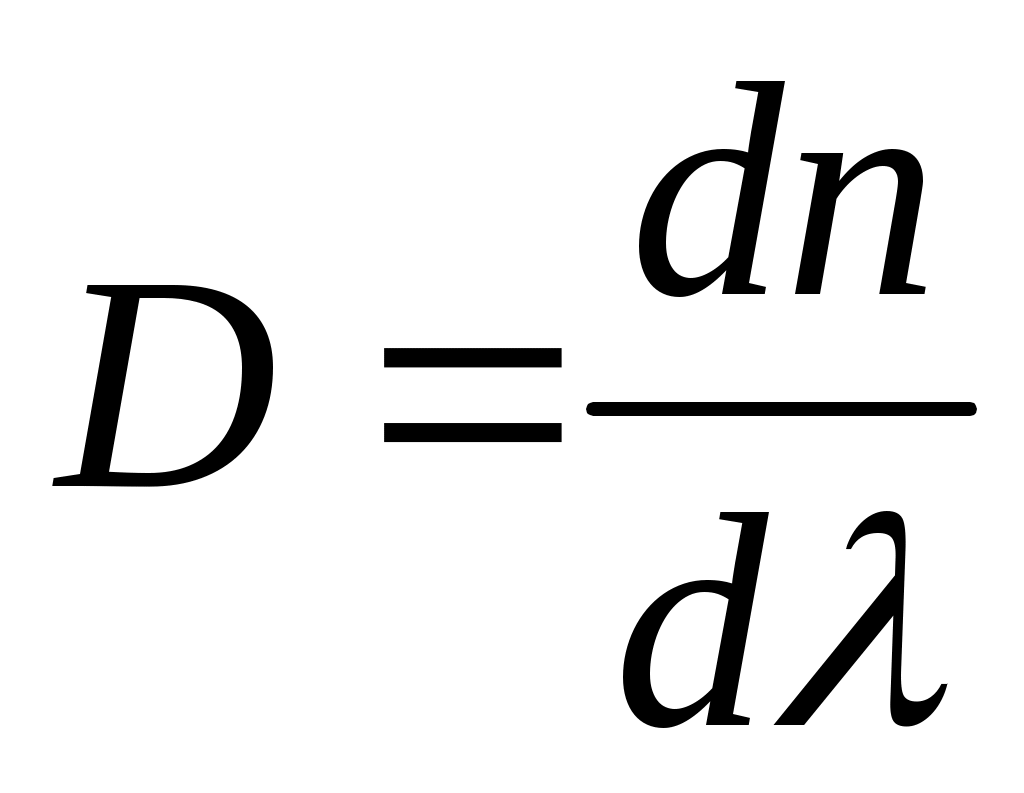 (13.1)
(13.1)
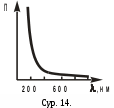 Толқын ұзындығы өскен сайын сыну көрсеткіші кемиді, бұл кәдімгі дисперсия деп аталады. Жарық толқын энергиясының ол заттарда таралған кезде энергияның деп аталады.
Толқын ұзындығы өскен сайын сыну көрсеткіші кемиді, бұл кәдімгі дисперсия деп аталады. Жарық толқын энергиясының ол заттарда таралған кезде энергияның деп аталады.
Жарық жұтылуы Бугер заңына бағынады
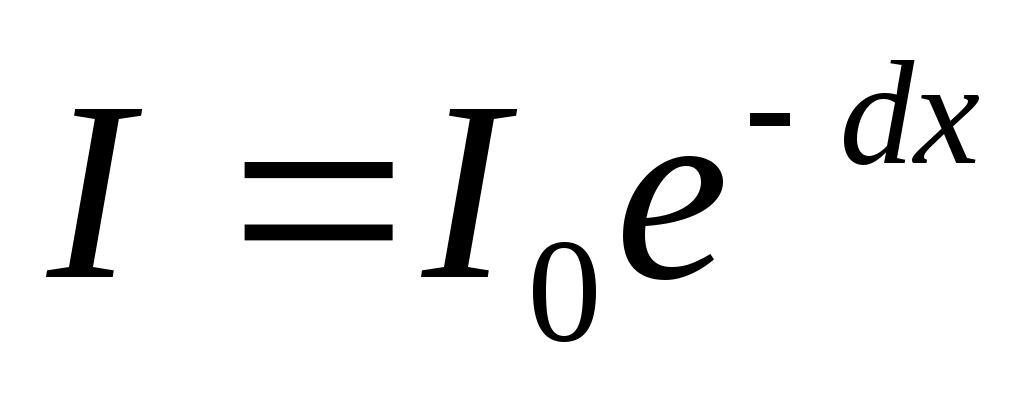 (13.2)
(13.2)
Мұндағы Іо, І қалыңдығы х болған жұтушы затта түскенде және өткендегі жарық интенсивтілігі, d – жұту коэффиценті деп аталады, ол жарық толқын ұзындығына, заттың химиялық табиғатына, күйіне байланысты.
Максвелл теориясы бойынша жарық толқындары көлденең – толқынның электр (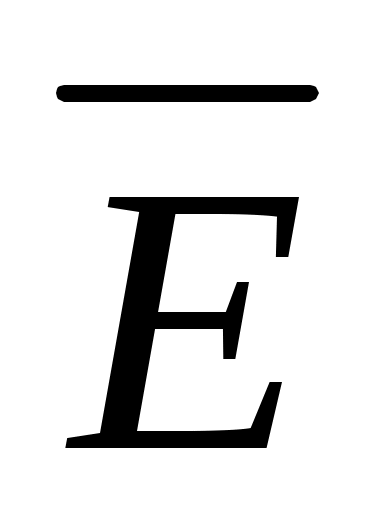 ) және магнит (
) және магнит ( ) өрістерінің кернеуліктері бір-біріне перпендикуляр және толқын таралу бағытына препендикуляр болады. Сондықтан жарықтың поляризациясының (үйектелуінің) заңдылықтарын білу үшін сол векторлардың біреуін зерттеу жеткілікті – көбінесе барлық ойлам жарық векторы туралы болады – электр өрісінің кернеулігі (
) өрістерінің кернеуліктері бір-біріне перпендикуляр және толқын таралу бағытына препендикуляр болады. Сондықтан жарықтың поляризациясының (үйектелуінің) заңдылықтарын білу үшін сол векторлардың біреуін зерттеу жеткілікті – көбінесе барлық ойлам жарық векторы туралы болады – электр өрісінің кернеулігі (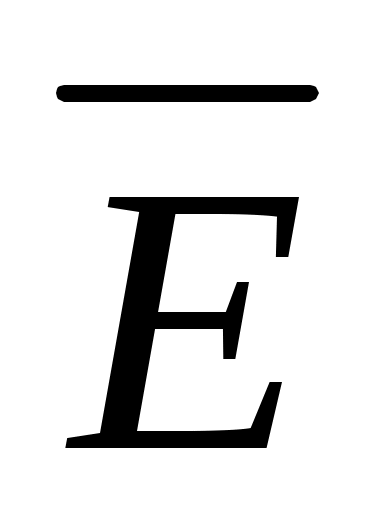 ) туралы.
) туралы.
Жарық көптеген атомдардың шығарып тұрған жинақтаушы электромагниттік сәуле шығарушы болып табылады. Атомдар бір-біріне тәуелсіз жарық толқындарын шығарып тұрғандықтан жарық векторының кез-келген бірдей ықтималдылықты бағыттарда тербелісі, мұндай жарықты табиғи жарық деп атайды. Жарық векторының тербелісі қандай да бір тәсілмен реттелінген болса, ондай жарықты поляризацияланған деп аталады. 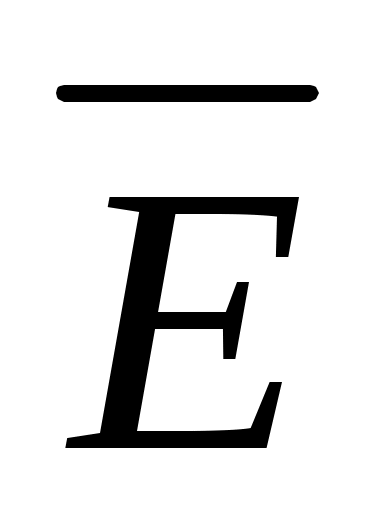 векторы тек бір бағытта тербеліп тұрса, ондай жарықты тегіс поляризацияланған деп атайды.
векторы тек бір бағытта тербеліп тұрса, ондай жарықты тегіс поляризацияланған деп атайды.
 Табиғи жарықты поляризатор деп аталатын заттардан өткізсе, олар тек белгілі бір бағыттағы тербелістерді өткізеді – ол тегіс поляризацияланады. Табиғи поляризатор ретінде көбінесе турмалин деген кристалдарды пайдаланады. Егер табиғи жарықты оптикалық оське параллель кесілген турмалин пластинасына перпендикуляр жіберсе оның интенсивтілік
Табиғи жарықты поляризатор деп аталатын заттардан өткізсе, олар тек белгілі бір бағыттағы тербелістерді өткізеді – ол тегіс поляризацияланады. Табиғи поляризатор ретінде көбінесе турмалин деген кристалдарды пайдаланады. Егер табиғи жарықты оптикалық оське параллель кесілген турмалин пластинасына перпендикуляр жіберсе оның интенсивтілік 
 тің өзгеруі байқалмайды. Егер жарық блогына тағы да бір турмалин пластинасын қойып, оны бұрса, онда пластиналардан өткен жарық интенсивтілігі кристалдардың оптикалық осьтері арасындағы α бұрышына байланысты Малюс заңы
тің өзгеруі байқалмайды. Егер жарық блогына тағы да бір турмалин пластинасын қойып, оны бұрса, онда пластиналардан өткен жарық интенсивтілігі кристалдардың оптикалық осьтері арасындағы α бұрышына байланысты Малюс заңы
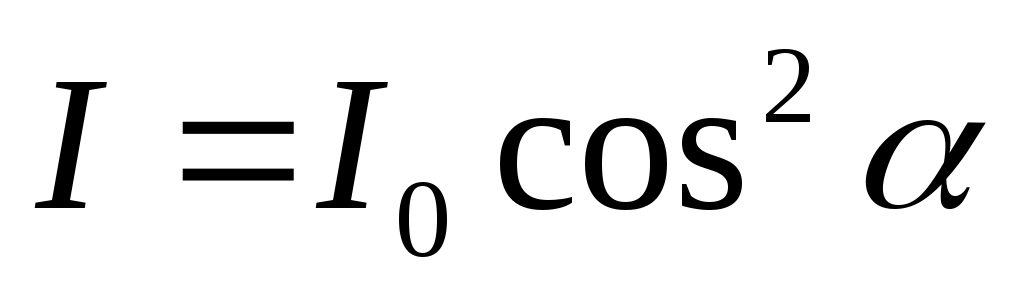 (13.3)
(13.3)
бойынша өзгереді. Мұндағы Іо және І ІІ кристалға түсетін және одан өтетін жарық интенсивтіліктері Т1 – поляризатор, Т2 – анализатор деп аталады. Поляризацияланған жарық алу үшін табиғи жарықты поляризатор мен анализатор болатын кристалдардан өткізу керек.
Брюстер заңы бойынша түсу бұрышының
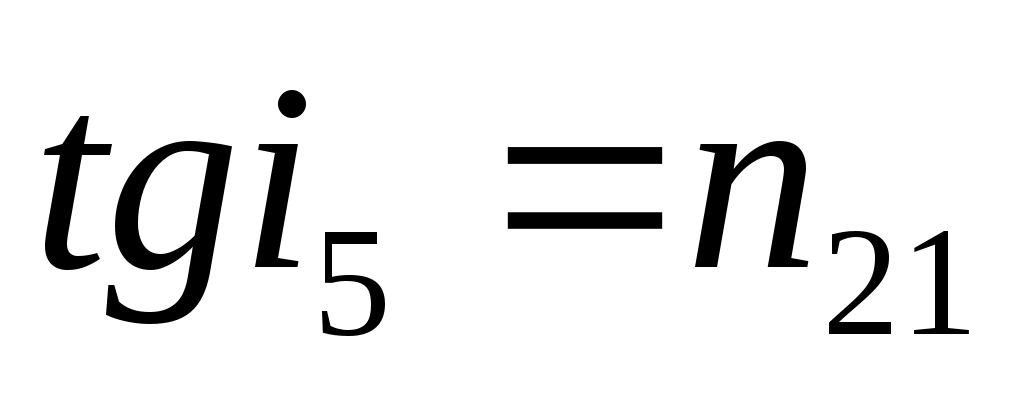 (13.4)
(13.4)
мәнінде шағылған нұр тегіс поляризацияланған болады. І5 – Брюстер бұрышы деп аталады, п21 – екінші ортаның біріншіге салыстырғандағы сыну көрсеткіші. Түсу бұрышы І5-ға тең болғанда сынған нұр ең көп поляризацияланады, бірақ толық емес.
Жеткіліктідей жоғары температураға дейін қыздырған денелер өзінен жарық шығарады, мұны жылулық сәуле шығару деп атайды. Жылулық сәуле шығарудың сипаттамасы есебінде денелердің энергиялық сәулеленуінің спектрлік тығыздығын
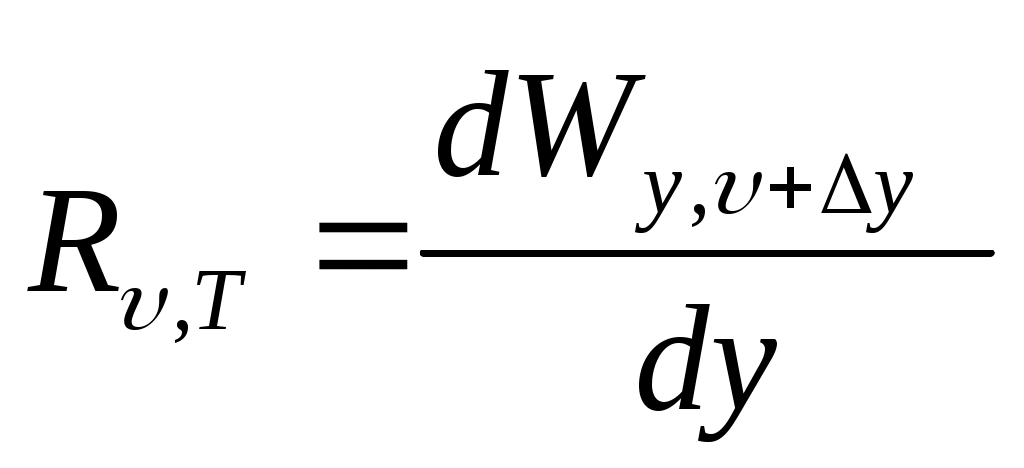 (13.5)
(13.5)
алады. Мұндағы 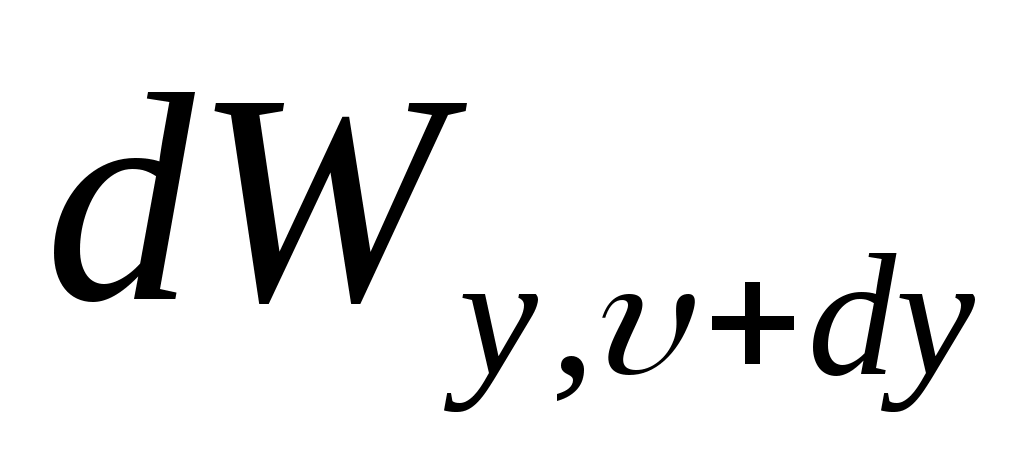 - уақыт бірлігінде дененің бірлік бет ауданынан
- уақыт бірлігінде дененің бірлік бет ауданынан  -дан
-дан  +d
+d жиілік интервалында шығып тұрған электромагниттік сәулелену энергиясы - өлшем бірлігі – Дж/м². Энергиялық сәулеленудің спектралдық тығыздығын білсе энергиялық интегралдық сәулеленуді де табуға болады:
жиілік интервалында шығып тұрған электромагниттік сәулелену энергиясы - өлшем бірлігі – Дж/м². Энергиялық сәулеленудің спектралдық тығыздығын білсе энергиялық интегралдық сәулеленуді де табуға болады:
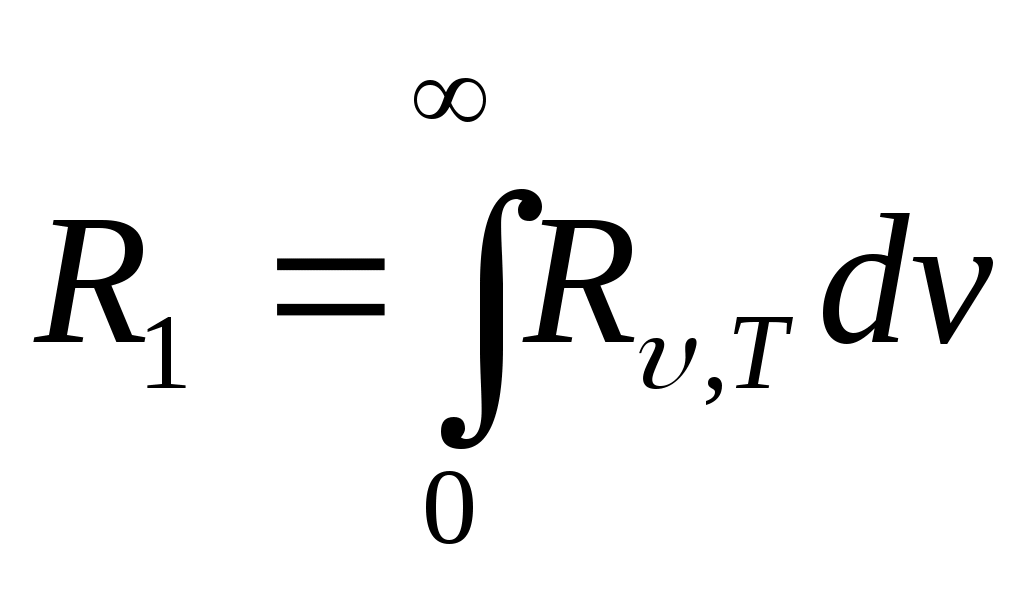 (13.6)
(13.6)
Денелердің түсіп тұрған сәулеленуді жұту қабілеттілігін спектралдық жұту қабілеттілік
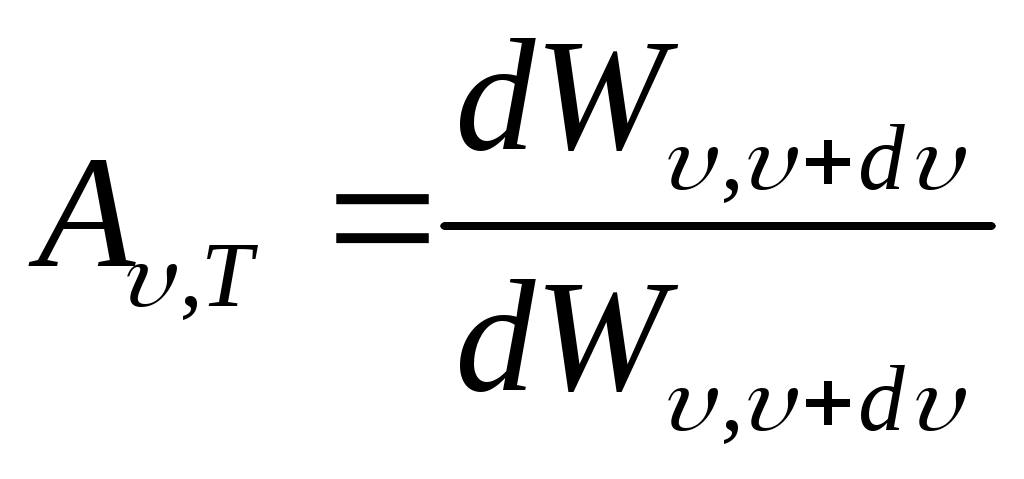 (13.7)
(13.7)
арқылы сипаттайды, ол денеге түсіп тұрған сәулеленудің қандай бөлшегі жұтылатынын көрсетеді. Түсіп тұрған сәулеленудің кез-келген температурада толық жұтатын денені қара дене деп атайды, демек ол үшін
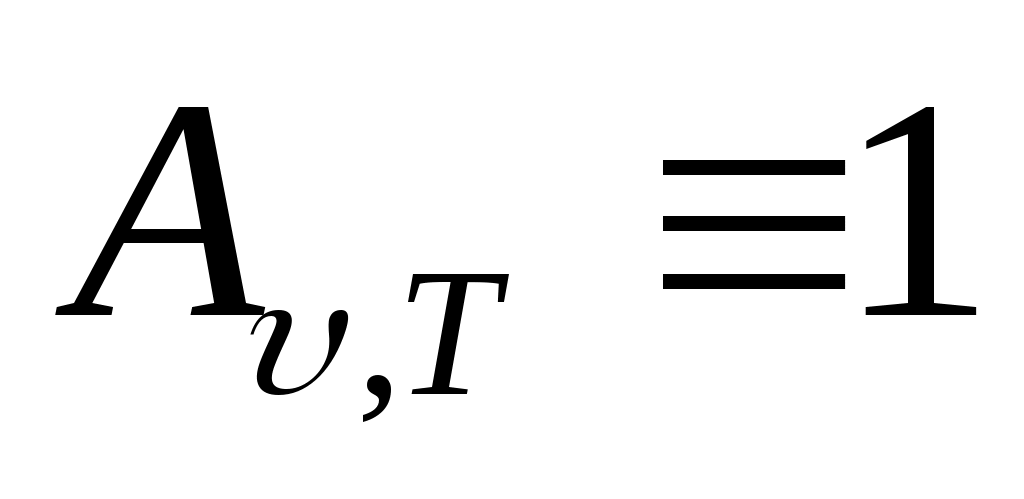 (13.8)
(13.8)
Кирхгоф заңы бойынша
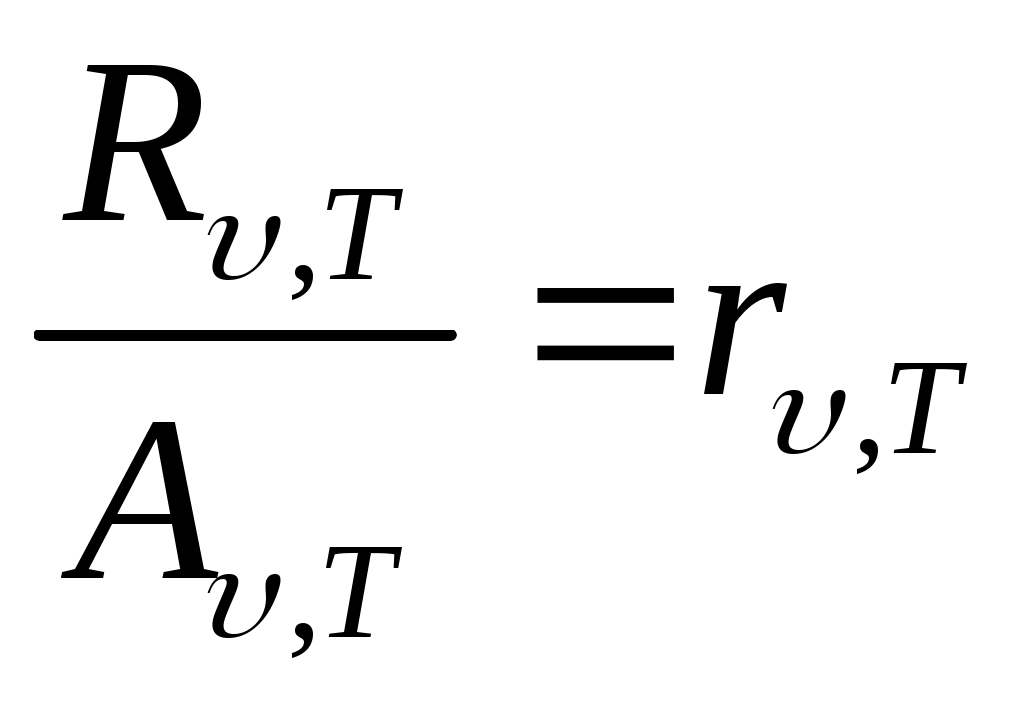 (13.9)
(13.9)
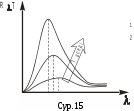
осы қатынас барлық денелерге де бірдей, тек жиіліктің және температураның әмбебап функциясы болып табылады.
Стефан-Больцман заңы бойынша
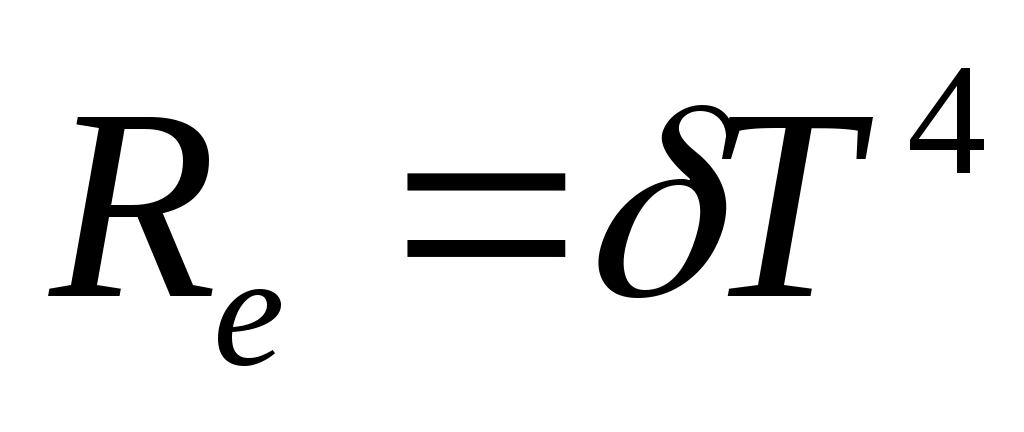 (13.10)
(13.10)
немесе қара дененің энергиялық сәулеленуі оның температурасының төртінші дәрежесіне пропорционал, мұндағы
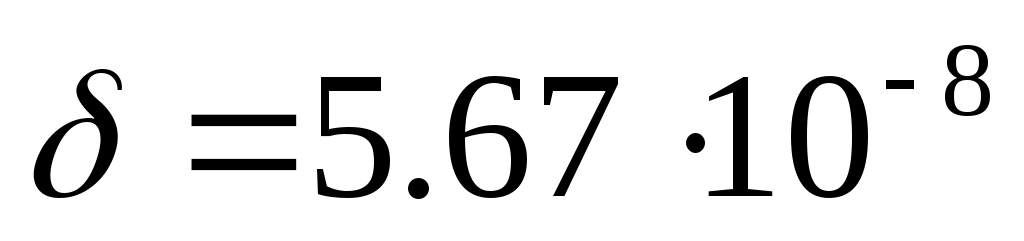 Вт/м²
Вт/м²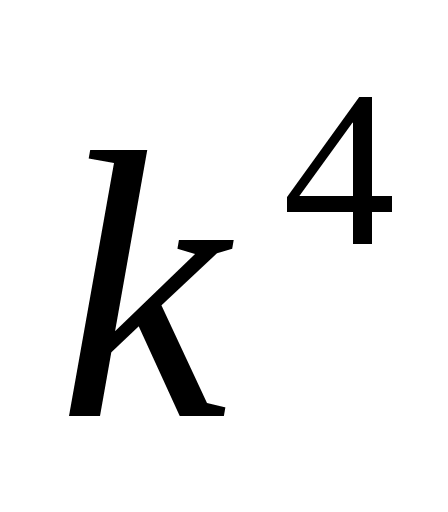 · - Стефан-Больцман тұрақтысы.
· - Стефан-Больцман тұрақтысы.
В. Вин ашқан ығысу заңы бойынша
λмах = в/т (13.11)
λмах – қара дененің энергиялық сәулеленудің максимал тығыздыққа сәйкес келетін толқын ұзындығы,
в=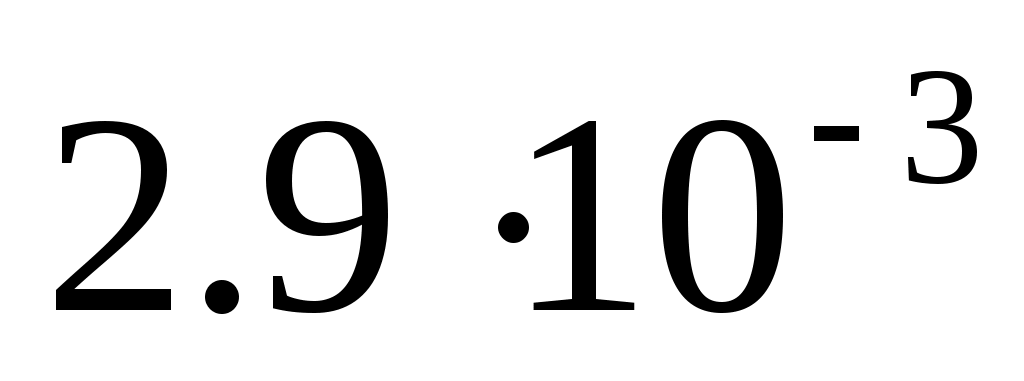 м·к – Вин тұрақтысы.
м·к – Вин тұрақтысы.
Қара дененің энергиялық сәулеленуінің спектралдық тығыздығы
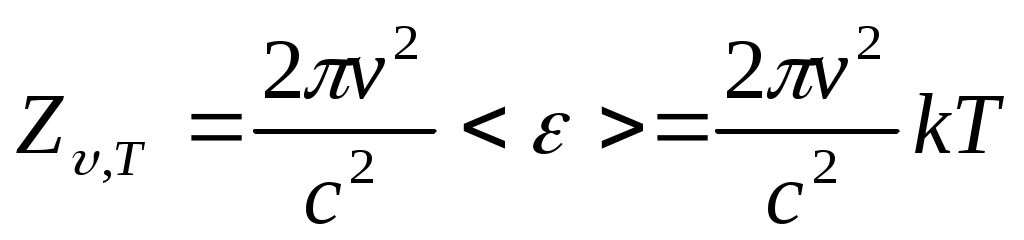 (13.12)
(13.12)
бұл Рэлей-Джинс формуласы. Бұл формула кіші жиіліктер мен үлкен температураларда эксперимент нәтижелерімен жақсы келіседі.
Планк шығарған Кирхгоф заңындағы әмбебап функция үшін формуласы
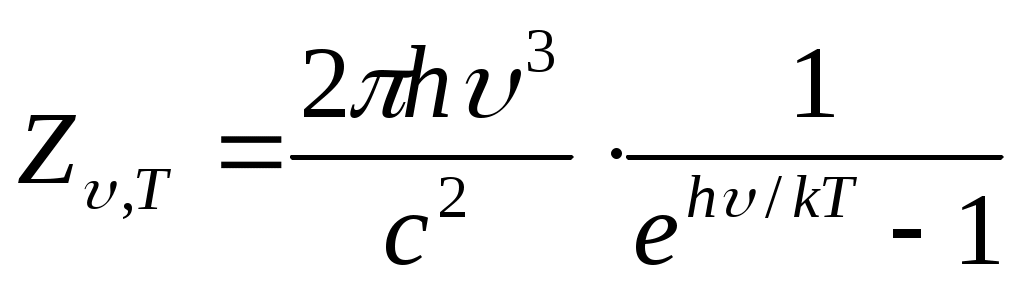 (13.13)
(13.13)
эксперимент нәтижелерімен барлық жиіліктер мен температураларда да жақсы келіседі.
Бұл функция Планк гипотезасына негізделген ол бойынша атом осцилляторлары энергияны үздіксіз емес, тек белгілі бір порциялармен-кванттармен ғана шығарады, ал квант энергиясы тербеліс жиілігіне пропорционал:

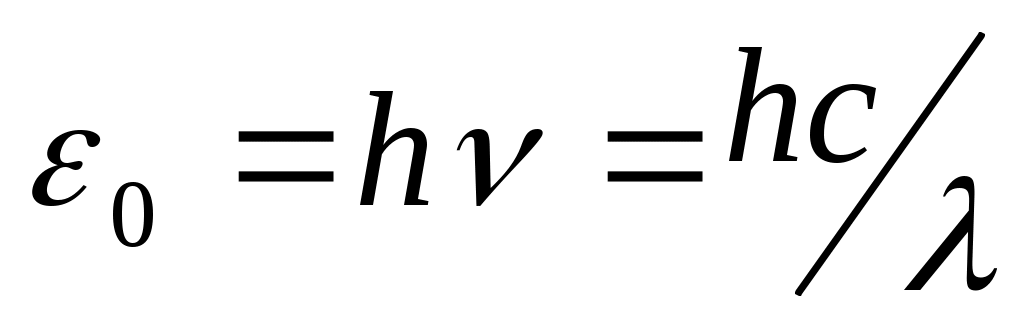
 (13.14)
(13.14)
мұндағы h=6.625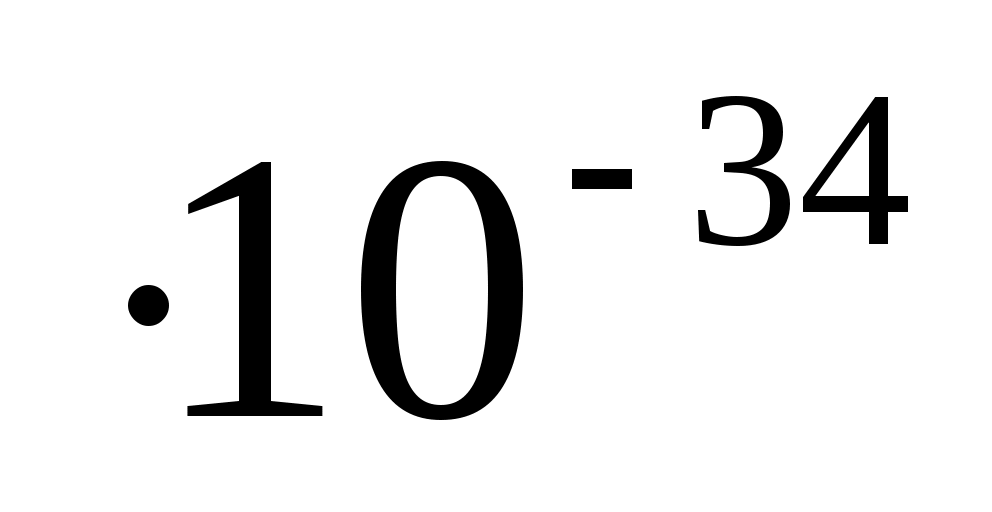 Дж*с – Планк тұрақтысы.
Дж*с – Планк тұрақтысы.
Электромагнит сәулелелену себебінен денелердің электрондарды сыртқа шығаруы сыртқы фотоэффект деп аталады.
Оны 1887 ж. Г. Герц ашқан, негізгі зерттеулерін А. Столетов жүргізген.
Электромагнит сәулелену себебінен шалаөткізгіштер мен диэлектриктер ішіндегі электрондардың байланысты күйден сыртқа шықпай еркіндік күйге өтуін ішкі фотоэффект деп аталады.
Әртүрлі екі шалаөткізгіш, немесе шалаөткізгіш пен металл контактын жарықтандырғанда ЭҚК пайда болуы вентильді фотоэффект дейді.
Сыртқы фотоэффект үшін Эйнштейн теңдеуі орындалады:
h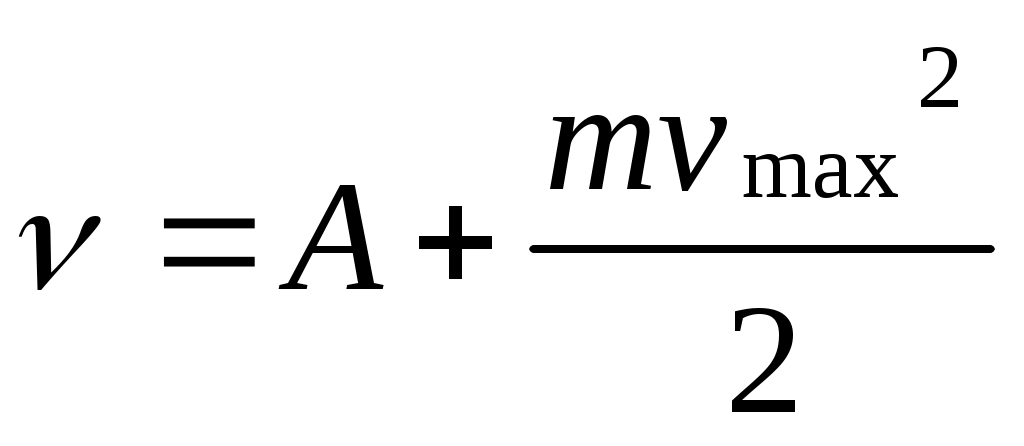 (13.15)
(13.15)
Мұндағы ٧- түсіп тұрған фотон жиілігі, А- металлдан шығу жұмысы,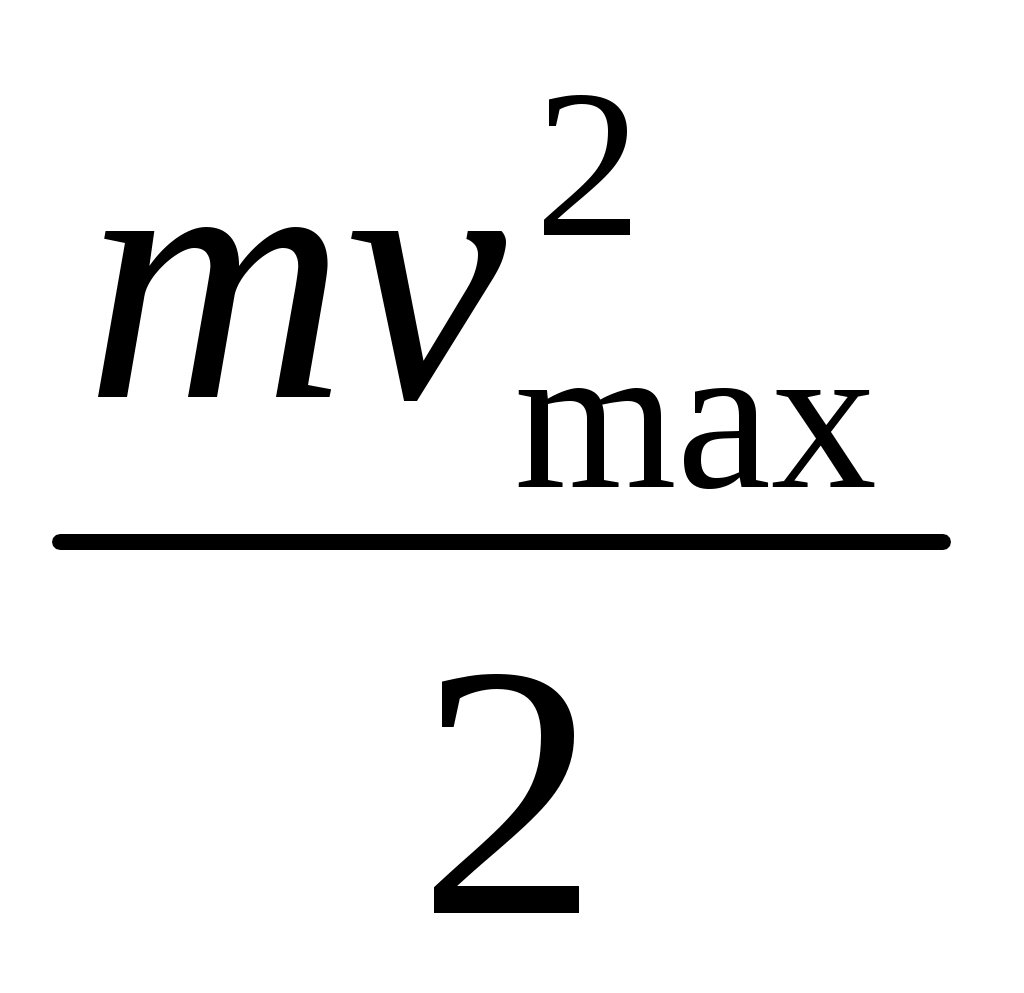 - шыққан фотоэлектронның максимал кинетикалық энергиясы, h- Планк тұрақтысы.
- шыққан фотоэлектронның максимал кинетикалық энергиясы, h- Планк тұрақтысы.
Фотоэффектінің қызыл шегі
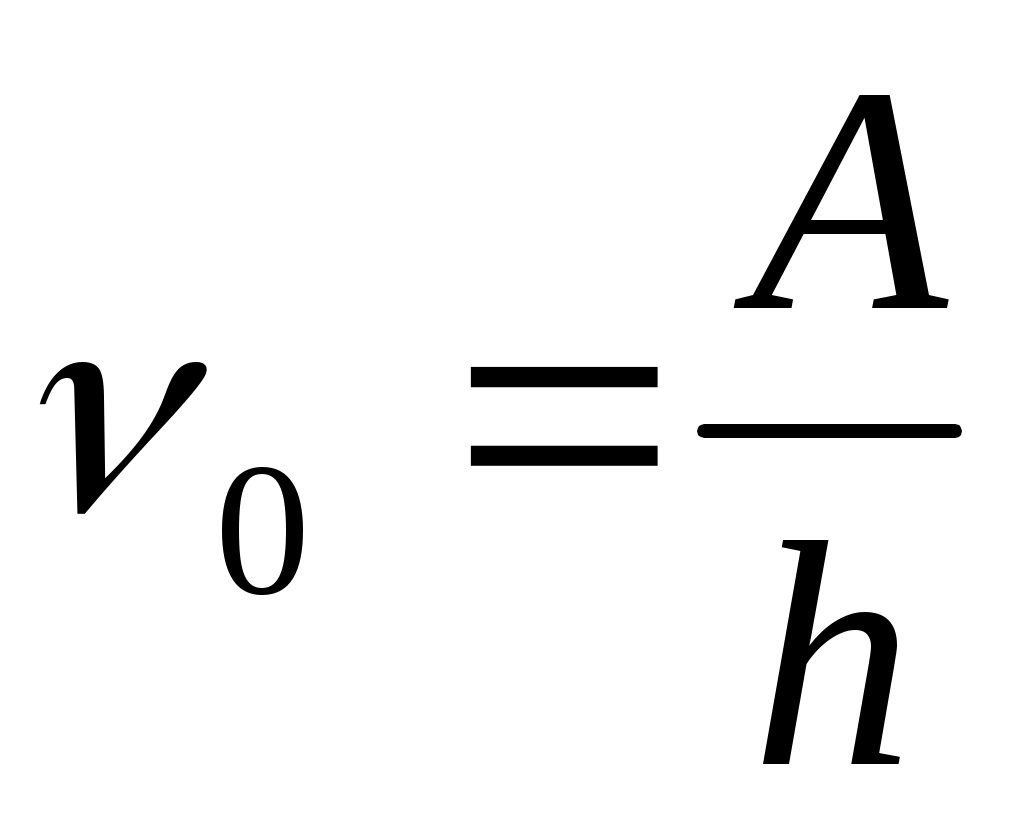 (13.16)
(13.16)
Фотоэффект құбылысы фотоэлементтерде, фотоэлектрондық көбейткіштерде, фоторезисторларда, вентильді фотоэлементтерде қолданылады.
Фотон массасы
m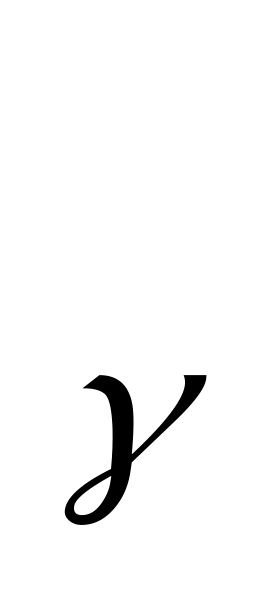 =
=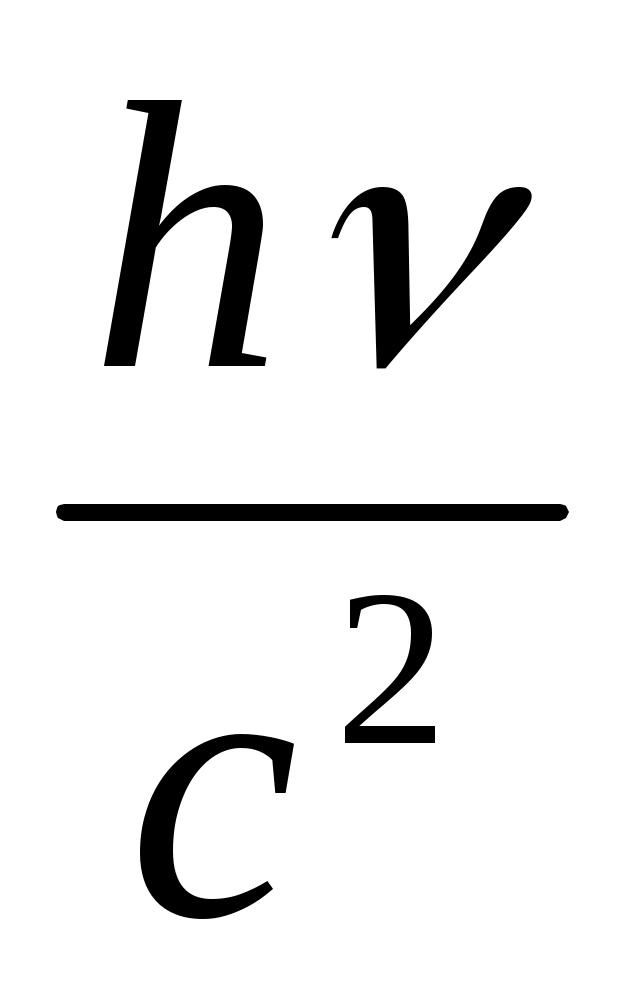 (13.17)
(13.17)
Фотон импульсі
p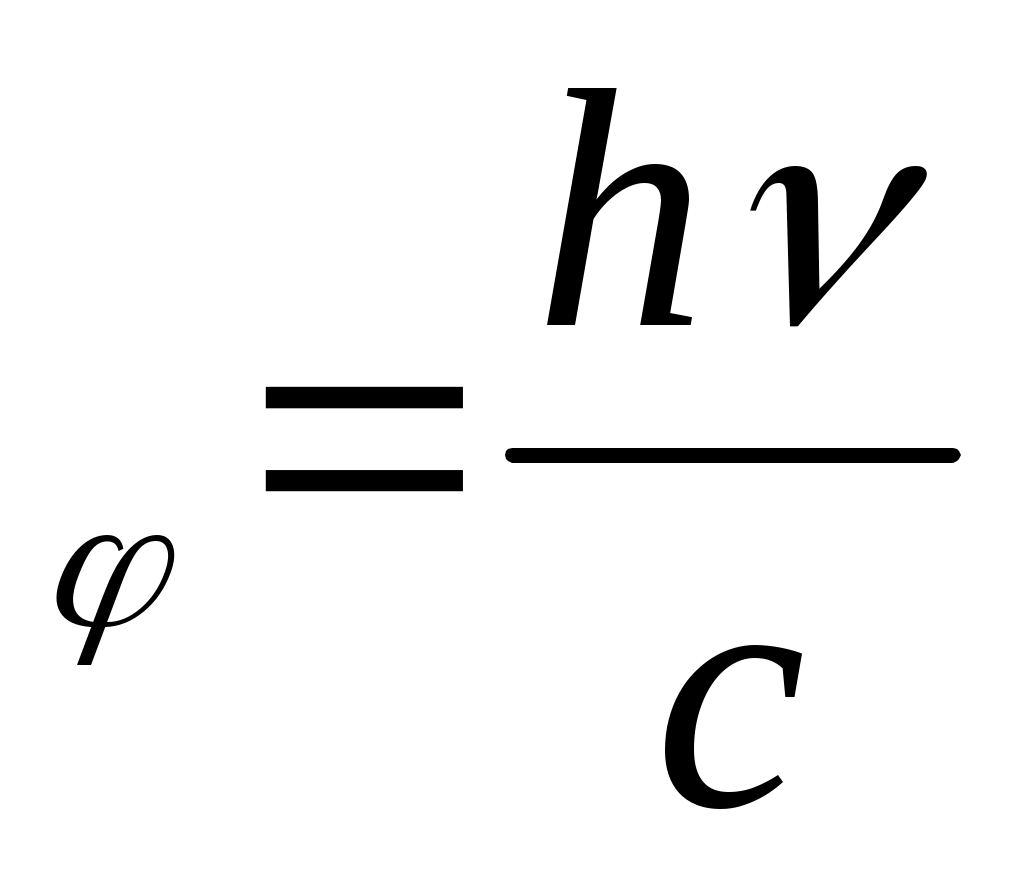 (13.18)
(13.18)
Жарық бетке нормаль түскенде оның осы бетке жасайтын қысымы
P=E/c(1+ )=w(1+
)=w(1+ ) (13.19)
) (13.19)
Мұндағы Е- түсіп тұрған фотондардың барлығының энергиясы, с- жарық жылдамдығы, w=E/c- сәулелену энергиясының көлемдік тығыздығы.
Жарық денеден шағылғанда оның толқын ұзындығының өзгеруі (өсуі) Комптон эффектісі деп аталады.
Осы өзгеру
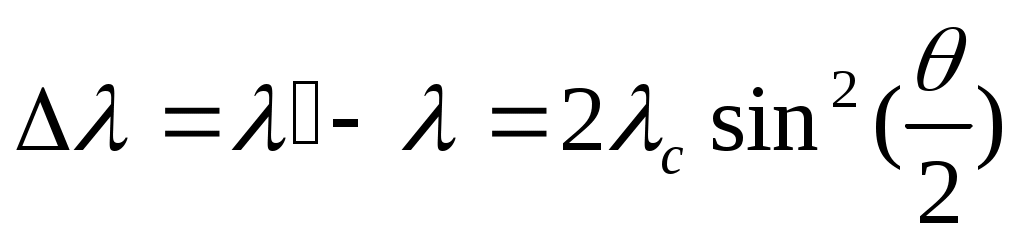 (13.20)
(13.20)
Мұндағы 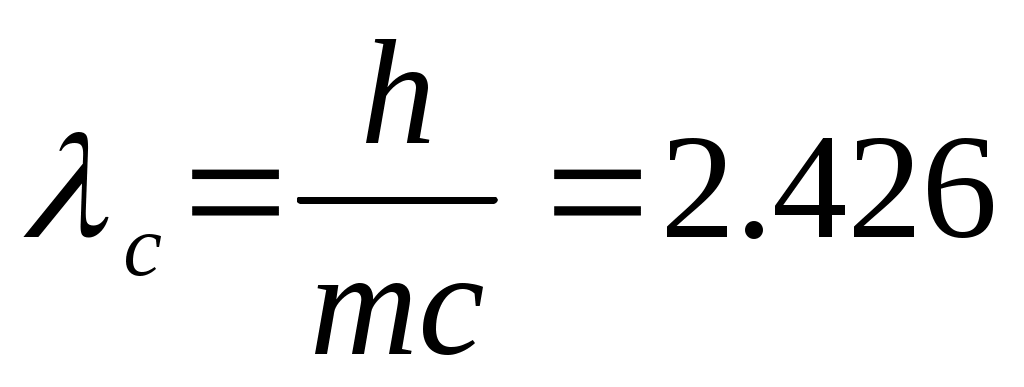 пм - Комптон толқын ұзындығы,
пм - Комптон толқын ұзындығы,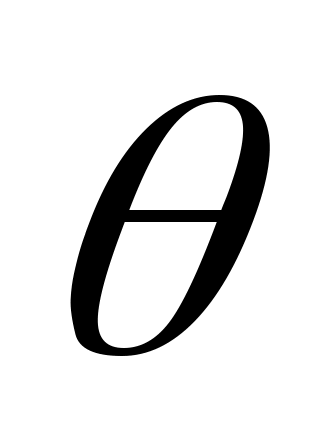 - шағылу бұрышы
- шағылу бұрышы
ЛЕКЦИЯ №14
Кванттық механика элементері. Кванттық электроника.
-
Корпускулалық толқындық дуализм.
-
Де Бройль гипотезасы.
-
Анықталмағандық қатынас.
-
Энергетикалық деңгейлер.
-
Спонтанды және еріксіз сәуле шығару. Лазерлер.
-
Паули принципі.
Біз кванттық оптика бөлімінде жарықтың әрі толқындық, әрі корпускулалық қасиеттерінің болатындығы туралы айтқан болатынбыз. Егер де жарықтың интерференция, дифракция, дисперсия, поляризация сияқты құбылыстары жарықтың толқындық қасиеттерін сипаттаса, ал фотоэффект, Комптон эффектісі жарықтың корпускулалық немесе кванттық табиғатын сипаттайды. Сонымен қатар, толқындық теорияда айтылғандай жарық тербеліс жиілігі мен толқын ұзындығы арқылы да сипатталып, ал корпускулалық теория бойынша жарық фотонның белгілі бір энергиясы , массасы және импульсі арқылы сипатталады. Олай болса, осы жарықтың екі түрлі табиғатын сипаттайтын шамалардың өзара байланысы болады. Енді осы айтылған пікірді былайша түсіндірейік. Корпускулалық теория бойынша жарық фотонының энергиясы мынаған тең
Когеренттік толқындар үшін cos(φ2 – φ1) = 1 болғанда max болатын нүктелерде І=4І, (І1=І2 болса), ал cos(φ2 – φ1) = -1 болатын нүктелерге min → І = 0 болады. Когеренттік емес толқындар үшін (φ2 – φ1) шамасы үздіксіз өзгеріп тұрады, сондықтан cos(φ2 – φ1) орташа мәні 0-ге тең болып барлық нүктелерде І=2І, (І1=І2). Когеренттік жарық толқындарын алу үшін бір толқын көзінен шыққан толқынды екіге бөліп қайта оларды түйістіреді, сүйтіп интерференция көрінісін бақылауға болады. Сонда бақылап тұрған нүктегегі тербелістер фаза айырмасы
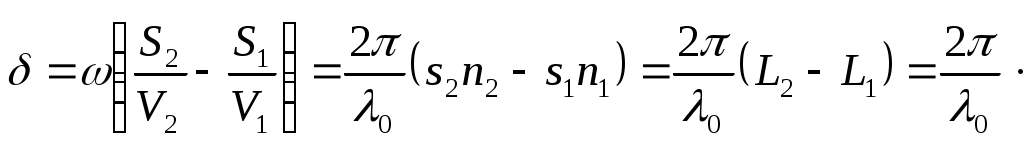 (12.18)
(12.18)болады (
Егер оптикалық жол айырымы вакуумдегі толқын ұзындықтарының бүтін санына тең болса
▲= ± m λ0 (m = 0, 1, 2, ...) (12.19)
онда ▲= ± 2mπ болып осы нүктеде қозған екі толқын да бір фазада болып бір-бірін күшейтеді, бұл интерференция max шарты болып табылады. Егер де
▲= ± ( 2m + 1)
ол нүктедегі тербелістер қарама-қарсы фазада болады, тербелістер бір-бірін жояды, бұл интерференцияның минимум шарты болады.
Жарық интерференциясын жүзеге асыру үшін когерентті жарық шоқтары болу қажет, ол үшін әртүрлі әдістер пайдаланады. Лазерлер пайда болмастан бұрын бір көзден шыққан жарық шоқтарын бөліп кейін оларды қайтадан тоғыстыру нәтижесінде интерференцияны көру мүмкін еді.
Оған мысалдар: Юнг тәсілі, Френель бипризмасы мен айнасы және т.б.
Интерференция көкжиегінде интенсивтіліктің
 максимумдері:
максимумдері: Х max = ±
минимумдері:
Х min = ±
нүктелерінде көрінеді.
Ньютон сақиналары тең қалыңдық жолақтарына айқын мысал. Ондағы (шағылу жарық үшін) max шарты:
min шарты:
Өтуші жарық үшін max және min шарттары осы шарттардың орын ауыстыруы болады. Интерференция құбылысы интерферометр деп аталатын дәл өлшеуші аспаптарда пайдаланады.
Майкельсон интерферометрі жәрдемімен жоғары дәлдікпен (
Жарықтың затта таралуы.
Жылулық сәулелену.
Абсолют қара дененің сәуле шығару қабілеті.
Кванттық гипотеза және Планк формуласы. Фотондар.
Фотоэффект.
Комптон эффектісі.
Корпускулалық толқындық дуализм.
Де Бройль гипотезасы.
Анықталмағандық қатынас.
Энергетикалық деңгейлер.
Спонтанды және еріксіз сәуле шығару. Лазерлер.
Паули принципі.
| . | (14.1) |
Эйнштейннің салыстырмалылық теориясы бойынша осы энергия фотонның массасымен мынадай байланыс болады
| . | (14.2) |
Осы екі теңдіктен фотонның массасы мен импульстің мына түрде жазуға болады
Француз физигі Луи де Бройль корпускулалық толқындық дуализмнің әмбебаптығы туралы гипотезасын ұсынды. Де Бройль ұсынысы бойынша әртүрлі микробөлшектерменжағынан корпускулалық сипаттамалар – энергия Е және импульс Ρ, ал екінші жағынан толқындық сипаттамалар- жиілік ٧ және толқын ұзындығы λ байланысты болады.
Олардың байланыстылылығы
E=h
Сонымен Де Бройль гипотезасына сәйкес әрбір импульске ие бөлшекке толқын ұзындығы
Болған толқындық процессі сәйкес келеді. (14.4) өрнегі Де Бройль формуласы деп аталады.
Электронға сәйкес толқын ұзындығы атомдар арақашықтарымен шамалас болғанда электрондық дифракция көрінеді. Бұл дифракция кезінде Вульф – Брэггтер формуласына
2dsinφ=mλ (m=1,2,3…) (143.5)
Сәйкес бұрыштарда дифракциялық максимумдар көрінеді.
Кеңес физигі П.С.Тартаковский баяу қозғалатын электрондар шоғының да жұқа слюда пластинадан өткізіп дифракция құбылысын байқады.
Көптеген тәжірибелерден атомдар мен молекулалардың шоқтары кристалдан шағылғанда да дифракция құбылысының байқалатындығын 1930ж. Штерн зерттеді. Қазіргі уақытта протон, нейтрон сияқты бөлшектердің де дифракциясы байқалады. Сөйтіп қазіргі кезде тәжірибе жүзінде тек электронның толқындық табиғаты ғана емес, басқа ұсақ бөлшектердің де толқындық қасиеттерінің бар екендігі толығымен дәлелденеді.
Зат бөлшектерінің толқындық қасиеттерін оқып-зерттеудің ғылым мен техникада маңызы зор. Электрондар шоғының дифракциялану құбылысы молекулалар мен кристалдардың ішкі құбылысын зерттеу үшін қолданылады. Заттың құрылысын осылайша зерттеу ғылымының электронография және нейтронография әдістері деп аталады. Сөйтіп электрондық оптика ғылымының жаңа саласы ашылды.
Анықталмағандық принципі материя бөлшектерінің (электрондар, протондар, т.б.) корпускулалық-толқындық табиғаты болатындығын айқындайды. Сандық тұрғыдан анықталмағандық принципі былай тұжырымдалады: егер — жүйенің инерция центріндегі координатының анықталмағандық мәні, ал импульсының осіне проекциясының анықталмағандық мәні болса, онда осы анықталмағандықтардың көбейтіндісі Планк тұрақтысынан (һ) кем болмайды. Анықталмағандық принципі атом ішіндегі құбылыстардың заңдылықтарын түсіндіру және
кванттық механика саласының қалыптасуы кезінде аса маңызды рөль атқарды. В. Гейзенберг ұсынған анықталмаушылық принципіне сәйкес
Координаттардың(x ,y, z) анықталмаушылықтары мен импульстер анықталмаушылықтары (
Де Бройльтолқындарына сәйкес толқындық заң бойынша ықтималдылық амплитудасы толқындық заң бойынша өзгереді оны да толқындық функция деп атайды. ( немесе
W
Мұндағы
Сонымен микрообъект күйінде толқындық функциямен сипаттау статистикалық, ықтималдылылық болады – толқындық функция модулінің квадраты бөлшектің t моментте кеңістіктің x пен x+dx, y пен y+dy, z пен z+dz аумағында болатындығының ықтималдылығы болып табылады.
Сонда бөлшектің dv көлем элементінде болу ықтималдылығы
dW=
Ал
Ықтималдылық тығыздығының мәні болады, ал ықтималдылықты нормалау шарты
Бұл шарттың мағынасы – бөлшектің кеңістіктің әйтеуір бір нүктесінде бар екендігі.
Энергетикалық деңгейлер – кванттық механика заңдарына бағынатын кванттық жүйенің (электрондардан, протондардан, т.б. элементар бөлшектерден тұратын не атом ядросынан, атомдардан, молекулалардан, т.б. бөлшектерден құралған) стационар күйдегі энергиясының мүмкін мәндері. Байланысқан микробөлшектерден (мыс., атом ядросы, т.б) тұратын кванттық жүйенің ішкі энергиясы квантталады, яғни кванттық жүйесінің ішкі энергиясы жүйесінің орнықты күйіне сәйкес келетін белгілі бір дискретті мәндерді [Е
0, Е1, Е2,... (Е0<Е1<Е2...)] ғана қабылдайды.
Ең төменгі Е, мүмкін болған энергиялық деңгей негізгі, ал басқаларының барлығы (E
Атомдағы электронның күйі төрт кванттық сандармен анықталады.
-
бас кванттық сан n (n=1,2,3,…) -
орбитальдық кванттық сан l (l=0,1,2,…n-1) -
магниттік кванттық сан m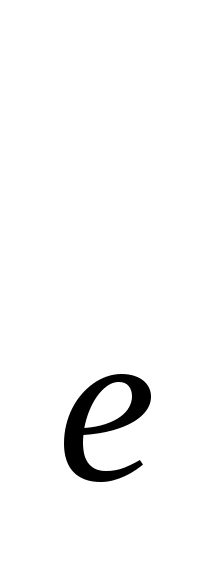 (
(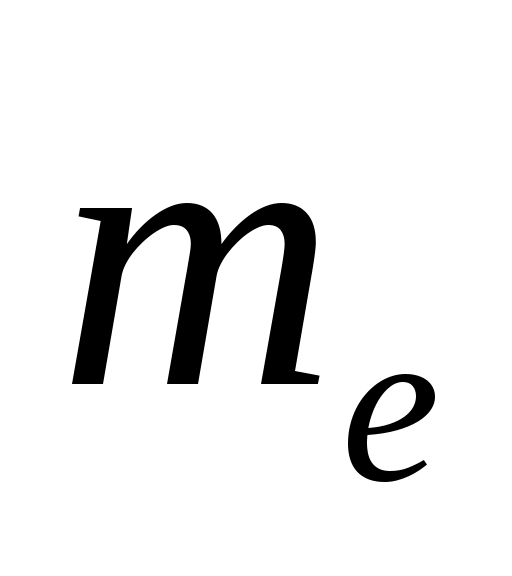 =-l,...-1,0,+1,…+l)
=-l,...-1,0,+1,…+l) -
спиндік кванттық сан m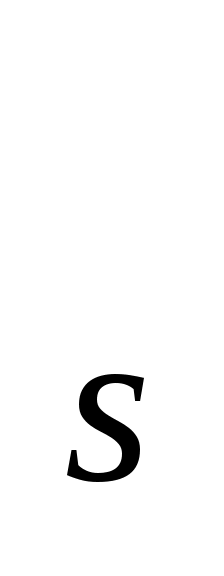 (m
(m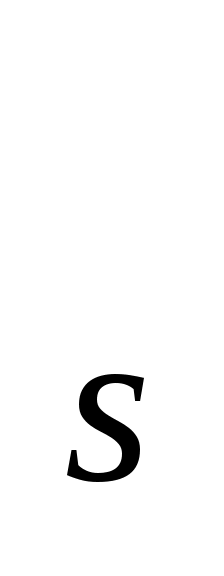 =+1/2, -1/2)
=+1/2, -1/2)
Берілген бас кванттық сан n болған электрондардың максимал саны :
Z(n)=
Атомдар энергияларды дискретті шамаларда E
Сыртқы әсерсіз қозған атомның фотон шығаруы тосын (өздігінен) сәуле шығару деп аталады.
Егер екі қозған күйдегі атомға сыртқы жиілігі
Осы құбылыс электромагнит толқындарды күшейтуге мүмкіншілік беріп кванттық жарық генераторын іске асыруға мүмкіншілік берді. Сонымен мәжбүри сәуле шығаруда екі фотон қатысады: қозған атомнан сәуле шығаруға себепші болатын бастапқы фотон, және атом шығарып тұрған екінші фотон. Екінші фотондар біріншісінен еш айырмашылығы жоқ, оның дәл көшірмесі болуы маңызды.
Орта өзіне түсіп тұрған сәулеленуді күшейтуі үшін жүйенің тепе теңдік емес (онда қозған күйдегі атомдар саны негізгі күйдегіден көп болуы керек)күйін жүзеге асыру керек. Мұндай күйлерді жайласудың