Файл: Методические указания по выполнению расчётнографической работы и организации самостоятельной работы содержание.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 321
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
ОБЩИЕ ТРЕБОВАНИЯ К ВЫПОЛНЕНИЮ И ОФОРМЛЕНИЮРАСЧЁТНО-ГРАФИЧЕСКОЙ РАБОТЫ
ПОЯСНЕНИЯ И ОБРАЗЕЦ ВЫПОЛНЕНИЯ ЗАДАНИЯ №2
ПО ТЕМЕ «ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
ПОЯСНЕНИЯ И ОБРАЗЕЦ ВЫПОЛНЕНИЯ ЗАДАНИЯ №3
ПО ТЕМЕ «ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
ПО ТЕМЕ «ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
ПО ТЕМЕ «ПАРНАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ»
ПОЯСНЕНИЯ И ОБРАЗЕЦ ВЫПОЛНЕНИЯЗАДАНИЯ №5
ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЗАЩИТЕЗАДАНИЯ №5
ПО ТЕМЕ «ТРЕНД-СЕЗОННЫЕ МОДЕЛИ ВРЕМЕННЫХ РЯДОВ»
ПОЯСНЕНИЯ И ОБРАЗЕЦ ВЫПОЛНЕНИЯЗАДАНИЯ №6
.
Данные_–_Анализ_данных'>Решение.
1. Для выбора фактора по данным индивидуального варианта задания необходимо построить матрицу линейных коэффициентов корреляции в MS Excel: вкладка Данные – Анализ данных – инструмент Корреляция. Если Пакет анализа в MS Excel ранее не был активирован, то вначале требуется его активация.
Активация Пакета анализа
Чтобы работать с надстройкой Анализ данных MS Excel, сначала ее надо подключить. Для этого нажмите Файл – Параметры. Далее в меню слева выберите Надстройки. Затем в разделе Управление выберите Надстройки Excel и нажмите кнопку Перейти(рис. 1).
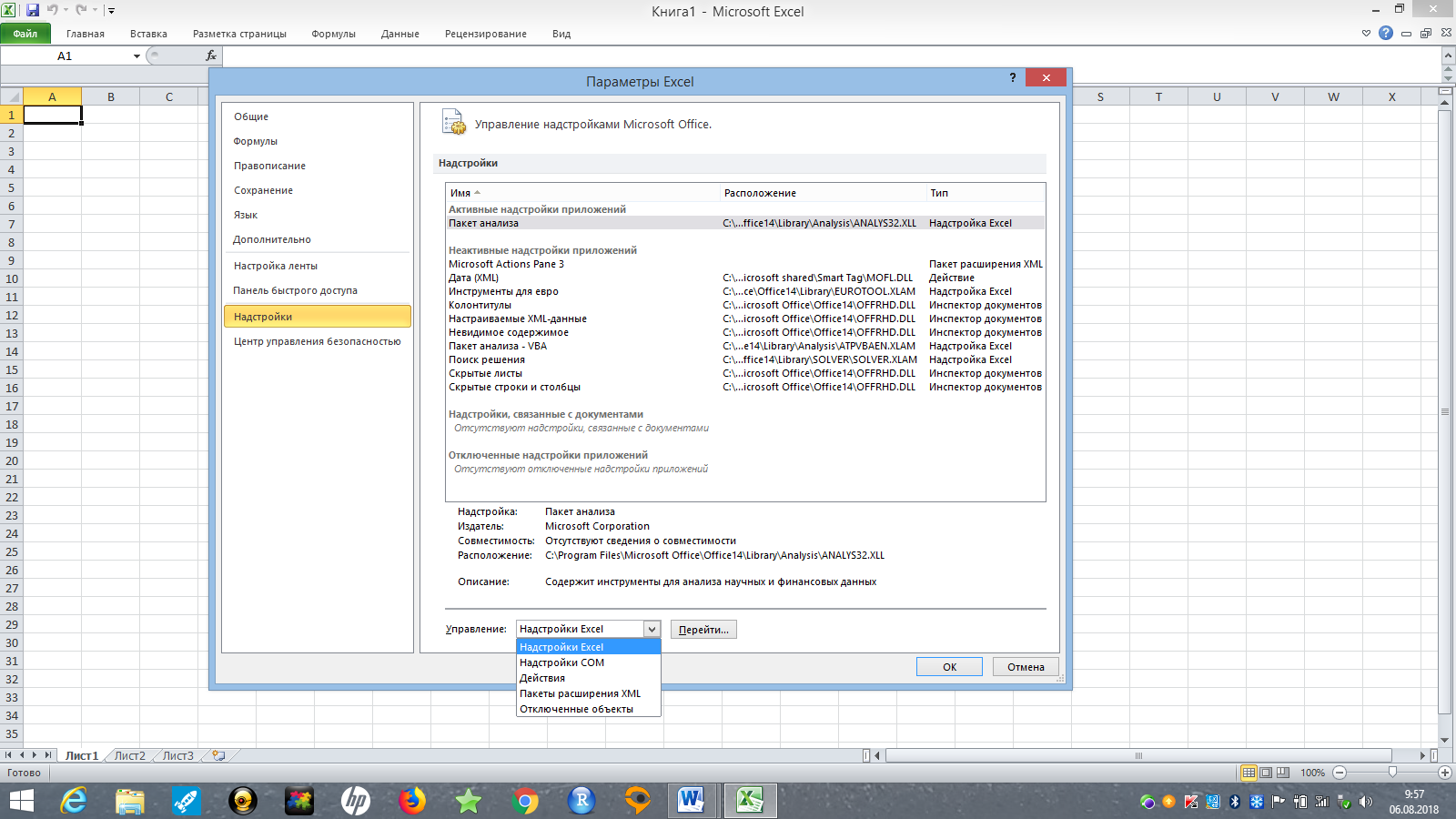
Рис. 1. Включение надстроек в Excel
В появившемся окне выберите надстройку Пакет анализа, поставив галочку напротив названия этого расширения (рис. 2).
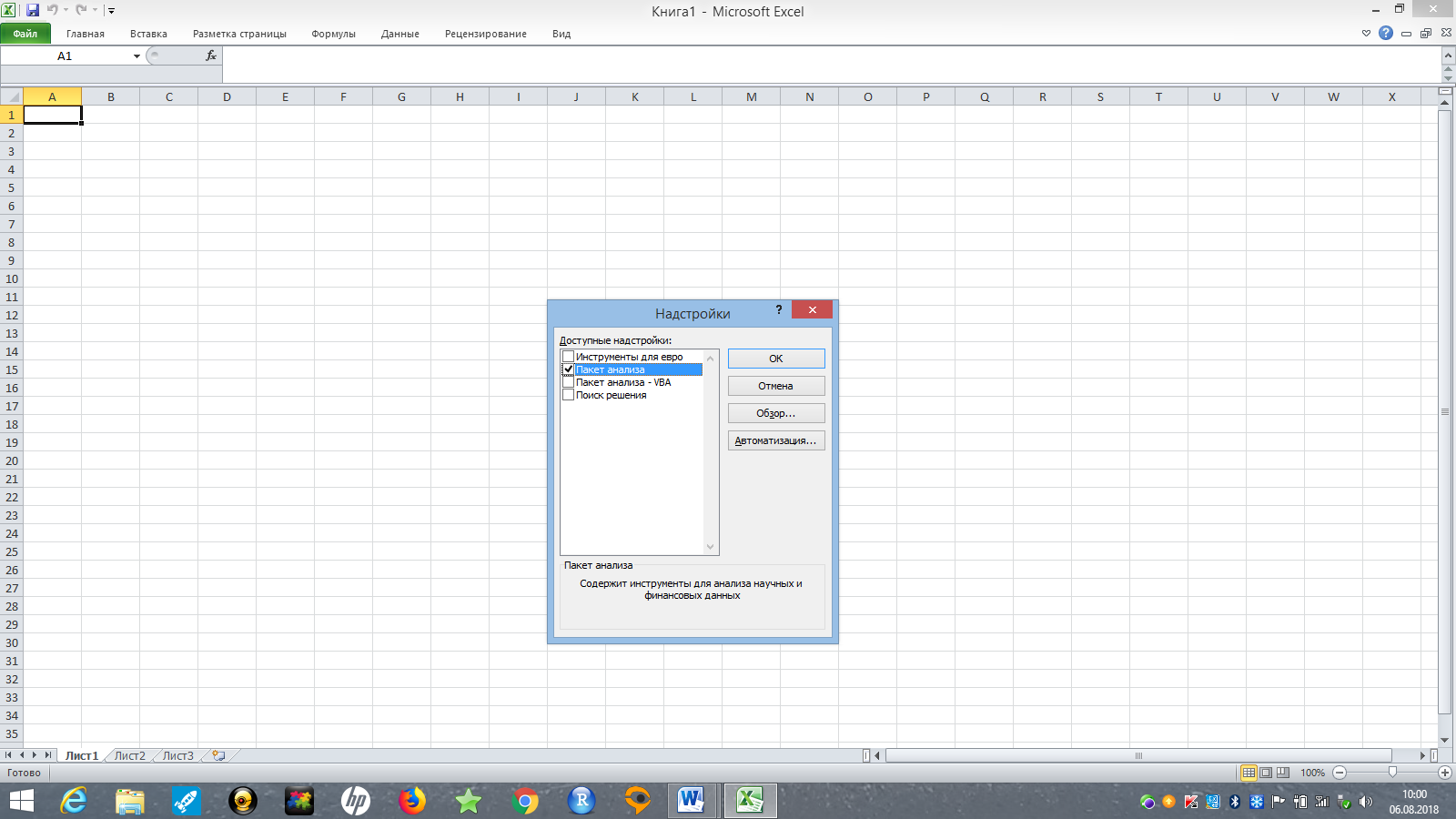
Рис. 2. Включение анализа данных в Excel
Теперь в главном меню программы на вкладке Данные (в верхней строке) появилась опция Анализ данных(рис. 3). Ее мы и будем в дальнейшем использовать.

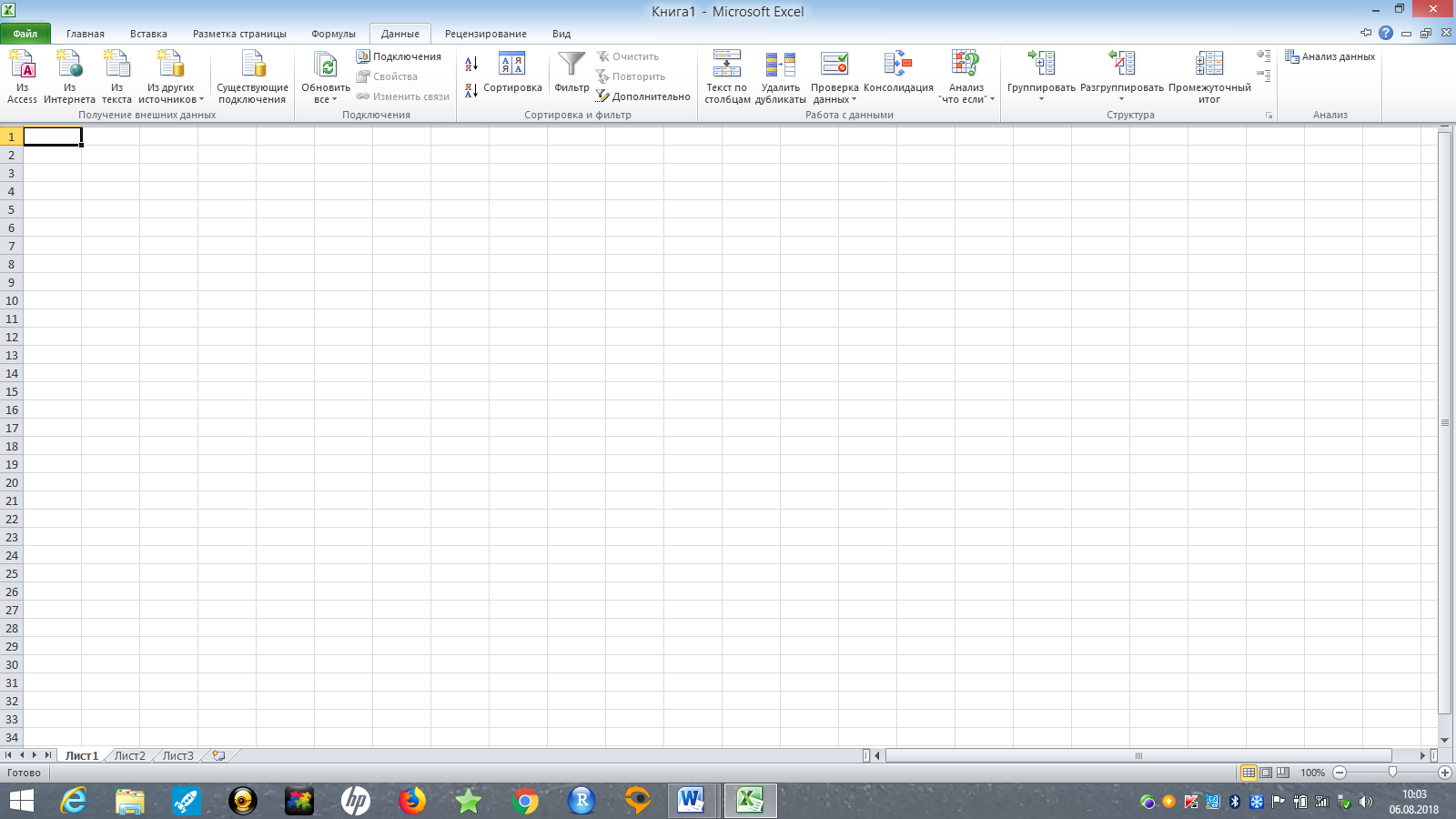
Рис. 3. Кнопка Анализ данных в Excel
Чтобы построить матрицу линейных коэффициентов корреляции необходимо применить инструмент КОРРЕЛЯЦИЯ надстройки Пакет анализа. Нажав на кнопку Анализ данных, следует выбрать опцию Корреляция (рис. 4).
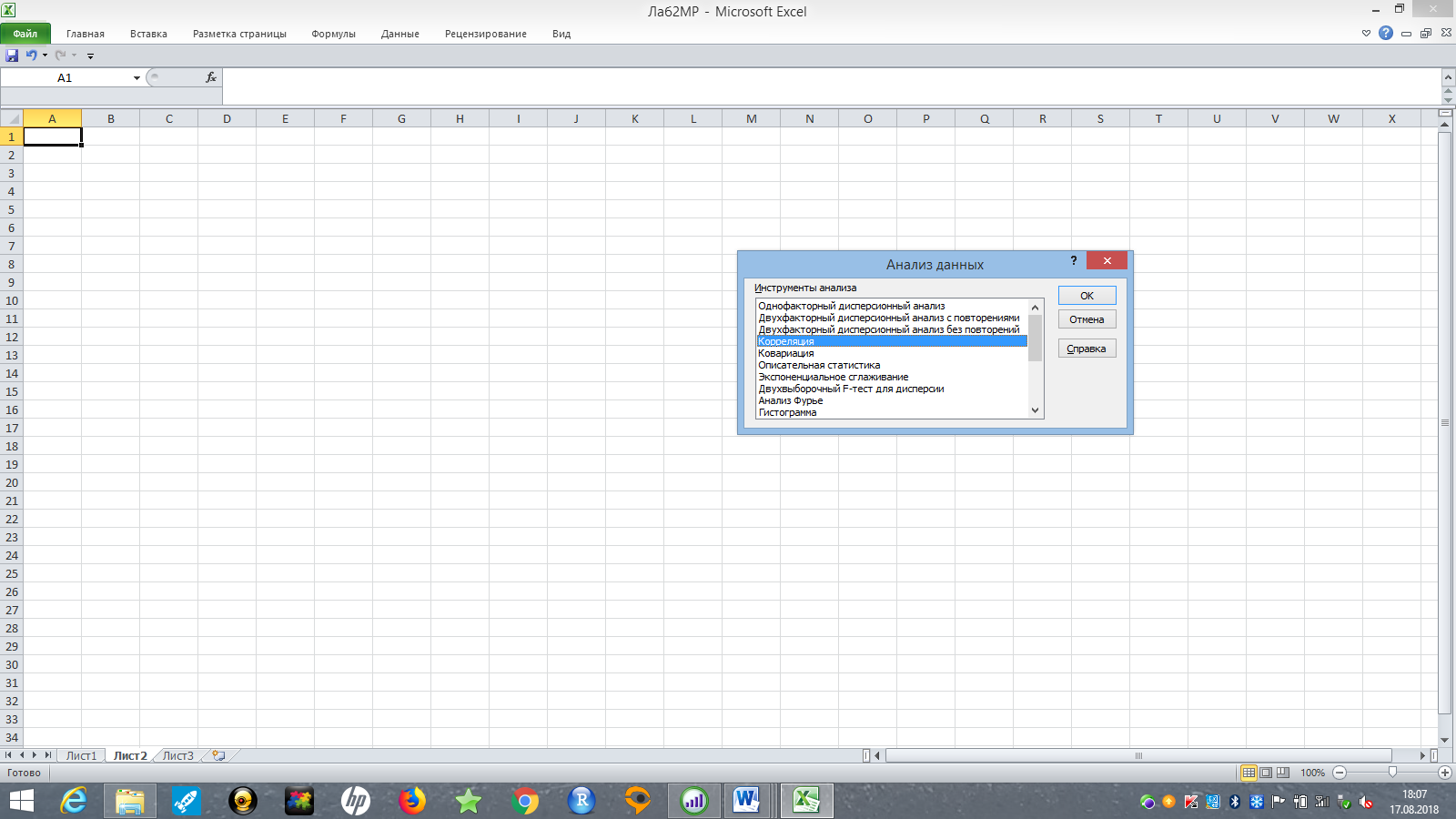
Рис. 4. Выбор корреляционного анализа в MS Excel
На экране появится новое окно с опциями корреляционного анализа (рис. 5).
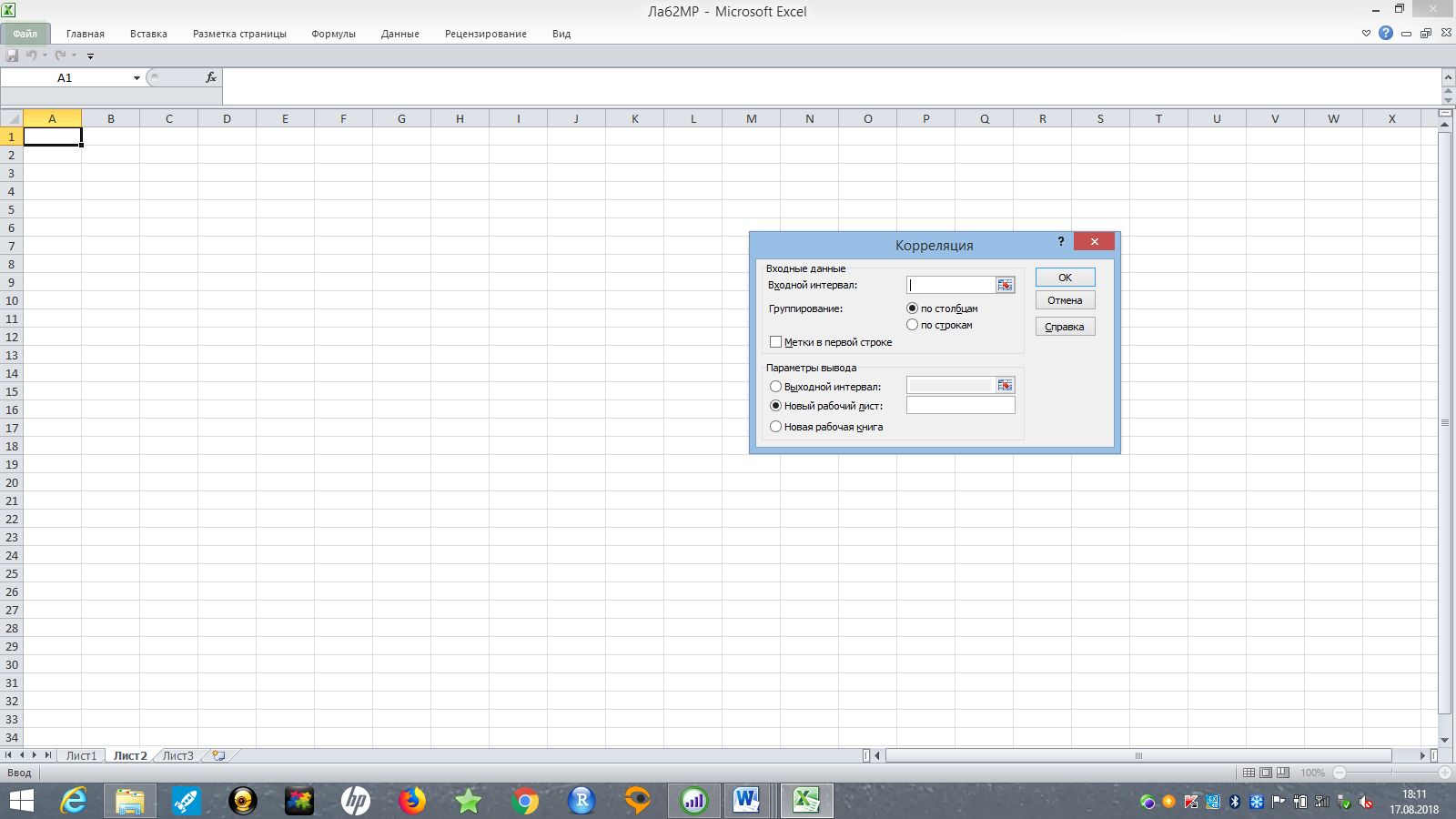
Рис. 5. Окно параметров корреляции в MS Excel
В поле Входной интервал необходимо выбрать таблицу со всеми исходными для корреляционного анализа. Опция «Группирование» дает возможность группировать переменные в таблице по столбцам (как принято традиционно) или по строкам. Опция
Метки, если в ней указать «галочку», трактует первую строку данных как названия переменных. В разделе Параметры вывода можно устанавливать, куда выводятся результаты корреляции (обычно выводят результаты на этот же лист, так как удобно держать данные и результаты корреляции на одном листе). Чтобы оценить корреляцию в MS Excel во входном интервале выделим диапазон переменных, укажем «галочку» в опции Метки, чтобы трактовать первую строку данных как названия переменных (рис. 6).
Рис. 6. Окно параметров корреляции с введенными значениями в MS Excel
Далее, нажав на кнопку Ок, получаем следующую матрицу линейных коэффициентов корреляции (рис. 7):
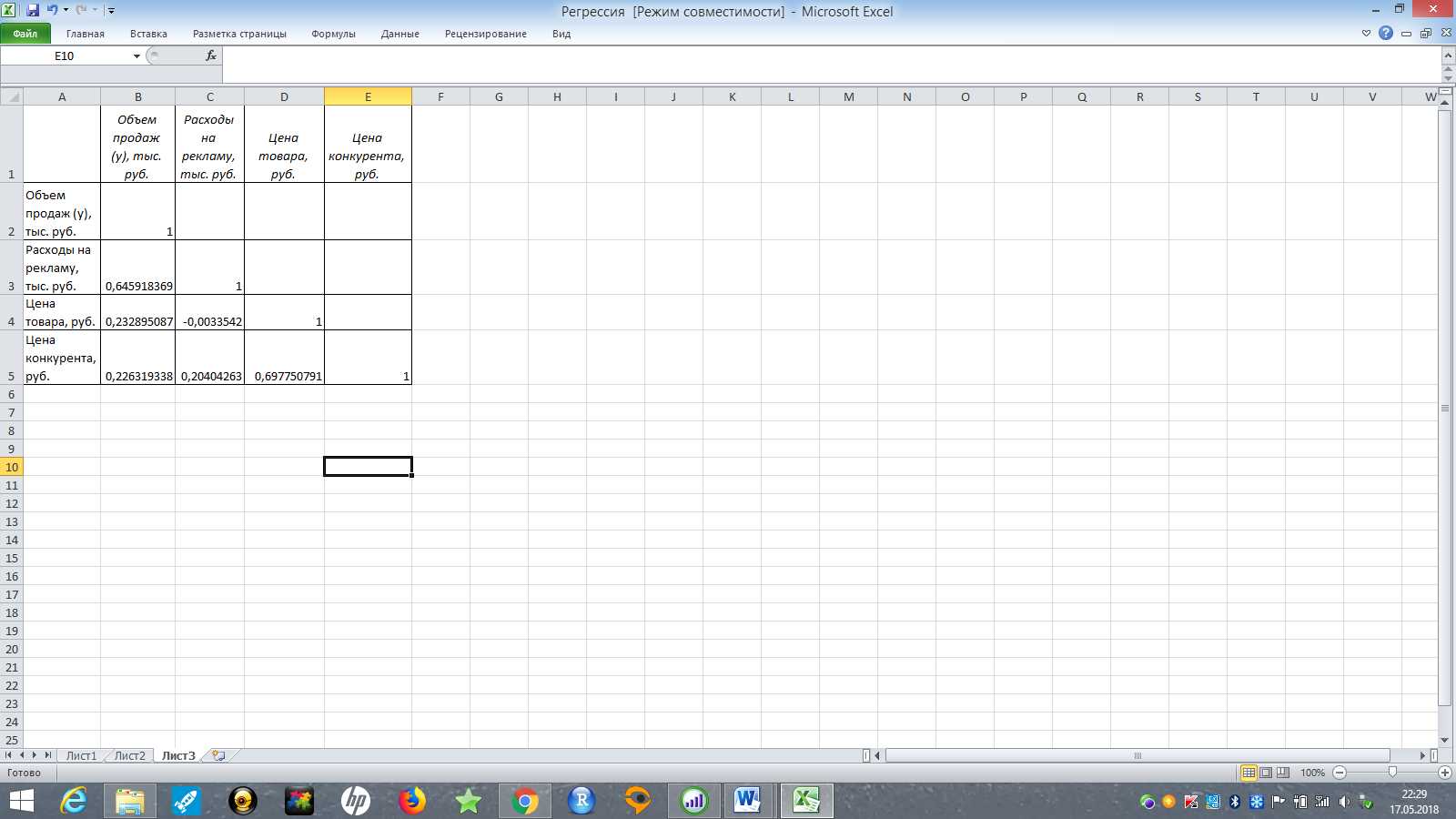
Рис. 7. Матрица линейных коэффициентов корреляции
По рисунку 7 видно, что наибольшее значение линейного коэффициента корреляции с зависимой переменной y принадлежит фактору Расходы на рекламу –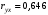 . Поэтому именно этот доминирующий фактор будем использовать для построения уравнения парной линейной регрессии.
. Поэтому именно этот доминирующий фактор будем использовать для построения уравнения парной линейной регрессии.
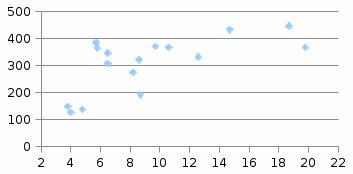
Рис. 8. Диаграмма рассеяния в MS Excel
Вывод 1: Как видно из рисунка 8, наблюдается прямая умеренная взаимосвязь между ценой за квартиру (y) и общей площадью (x). Точки на графике сосредоточены вокруг прямой линии, поэтому взаимосвязь ценой за квартиру и общей площадью уместно аппроксимировать прямой линией и применить линейную регрессию с одной объясняющей переменной.
Таблица 1
Подготовка данных для оценивания линейной регрессии объема продаж в зависимости от расходов на рекламу
Вывод 2: Запишем модель линейной регрессии: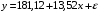 . Экономическая интерпретация коэффициентов следующая. Увеличение расходов на рекламу (х) на 1 тыс. рублей приводит при прочих равных условиях к увеличению объема продаж (y) в среднем на 13,52 тыс. рублей. Данный результат согласуется с экономической интуицией, так как при росте расходов на рекламу можно ожидать увеличения объема продаж. При отсутствии расходов на рекламу объем продаж может составить 181,12 тыс. руб.
. Экономическая интерпретация коэффициентов следующая. Увеличение расходов на рекламу (х) на 1 тыс. рублей приводит при прочих равных условиях к увеличению объема продаж (y) в среднем на 13,52 тыс. рублей. Данный результат согласуется с экономической интуицией, так как при росте расходов на рекламу можно ожидать увеличения объема продаж. При отсутствии расходов на рекламу объем продаж может составить 181,12 тыс. руб.
Вывод 3: Согласно шкале Чеддока-Снедекора наблюдается умеренная прямая статистическая взаимосвязь между объемом продаж и расходами на рекламу.
Вывод 4: Увеличение расходов на рекламу на 1 % приводит к увеличению объема продаж на 0,41%.
Чтобы вычислить дисперсии на 1 степень свободы, надо использовать ссылки на необходимые ячейки согласно формулам:
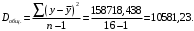
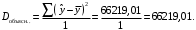
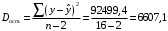
Проверить с использованием коэффициента корреляции и с помощью функции КВПИРСОН(…).
и с помощью функции КВПИРСОН(…).
Вывод 5: Доля дисперсии объема продаж, объясненная с помощью расходов на рекламу, составляет 42%. Чем ближе R2 к 1, тем лучше качество подгонки регрессии.
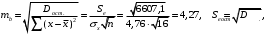
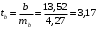 .
.
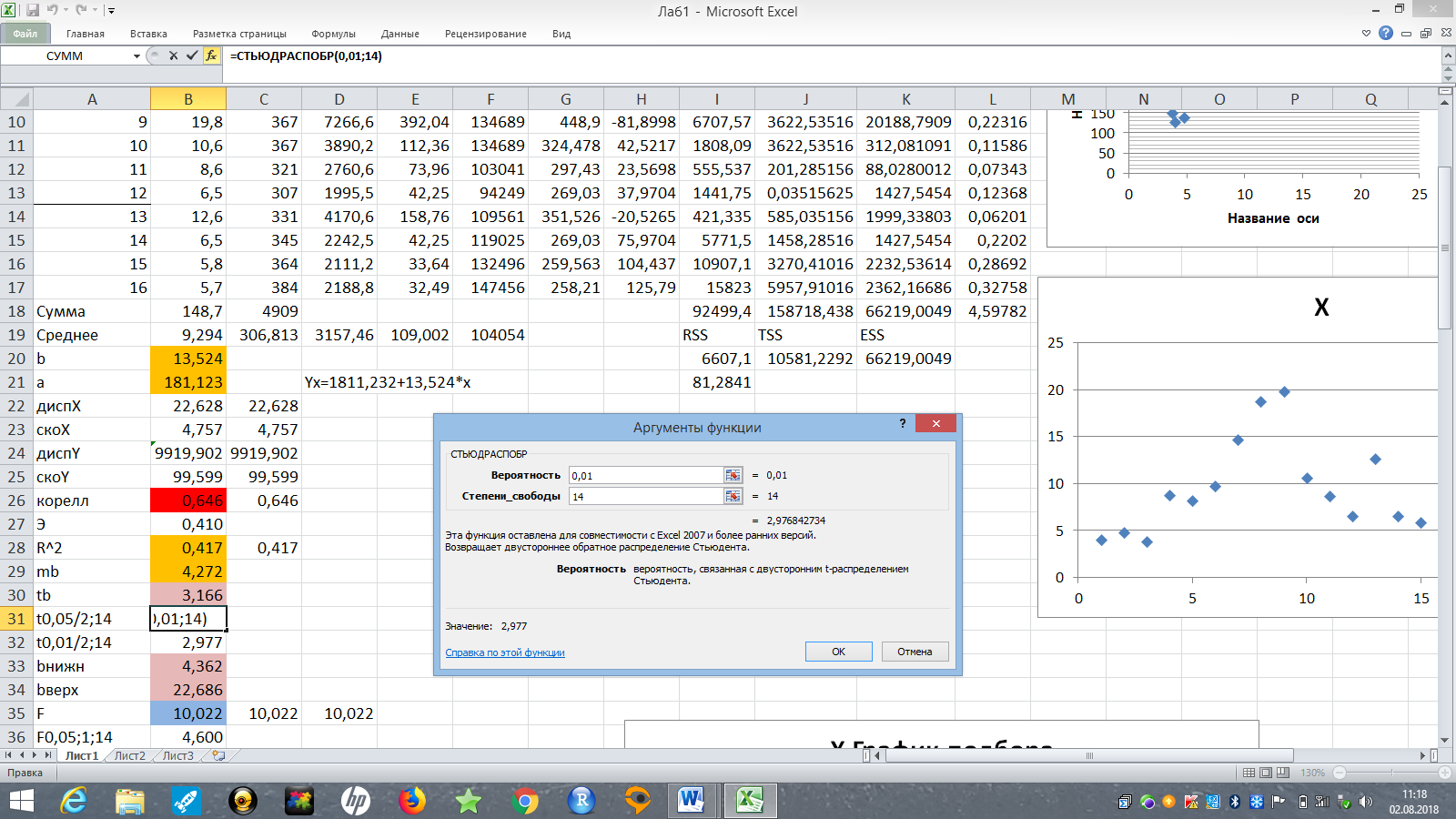
Рис. 9. Диалоговое окно функции СТЬЮДРАСПОБР(…).
Вывод 6: Поскольку 3,17 > 2,98, то гипотеза Н0: β = 0 отвергается, т.е. согласно тесту Стьюдента коэффициент регрессии β является значимым. Это означает, что между переменными x (расходы на рекламу) и y (объем продаж) существует значимая линейная связь.
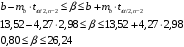
Вывод 7: Диапазон границ доверительного интервала для коэффициента регрессии в модели с хорошим качеством подгонки обычно не превышает 3. В нашем случае, правая граница больше, чем левая, более чем в 3 раза, значит, качество подгонки модели рекомендуется улучшать.
Данные_–_Анализ_данных'>Решение.
1. Для выбора фактора по данным индивидуального варианта задания необходимо построить матрицу линейных коэффициентов корреляции в MS Excel: вкладка Данные – Анализ данных – инструмент Корреляция. Если Пакет анализа в MS Excel ранее не был активирован, то вначале требуется его активация.
Активация Пакета анализа
Чтобы работать с надстройкой Анализ данных MS Excel, сначала ее надо подключить. Для этого нажмите Файл – Параметры. Далее в меню слева выберите Надстройки. Затем в разделе Управление выберите Надстройки Excel и нажмите кнопку Перейти(рис. 1).

Рис. 1. Включение надстроек в Excel
В появившемся окне выберите надстройку Пакет анализа, поставив галочку напротив названия этого расширения (рис. 2).

Рис. 2. Включение анализа данных в Excel
Теперь в главном меню программы на вкладке Данные (в верхней строке) появилась опция Анализ данных(рис. 3). Ее мы и будем в дальнейшем использовать.


Рис. 3. Кнопка Анализ данных в Excel
Чтобы построить матрицу линейных коэффициентов корреляции необходимо применить инструмент КОРРЕЛЯЦИЯ надстройки Пакет анализа. Нажав на кнопку Анализ данных, следует выбрать опцию Корреляция (рис. 4).

Рис. 4. Выбор корреляционного анализа в MS Excel
На экране появится новое окно с опциями корреляционного анализа (рис. 5).

Рис. 5. Окно параметров корреляции в MS Excel
В поле Входной интервал необходимо выбрать таблицу со всеми исходными для корреляционного анализа. Опция «Группирование» дает возможность группировать переменные в таблице по столбцам (как принято традиционно) или по строкам. Опция
Метки, если в ней указать «галочку», трактует первую строку данных как названия переменных. В разделе Параметры вывода можно устанавливать, куда выводятся результаты корреляции (обычно выводят результаты на этот же лист, так как удобно держать данные и результаты корреляции на одном листе). Чтобы оценить корреляцию в MS Excel во входном интервале выделим диапазон переменных, укажем «галочку» в опции Метки, чтобы трактовать первую строку данных как названия переменных (рис. 6).

Рис. 6. Окно параметров корреляции с введенными значениями в MS Excel
Далее, нажав на кнопку Ок, получаем следующую матрицу линейных коэффициентов корреляции (рис. 7):

Рис. 7. Матрица линейных коэффициентов корреляции
По рисунку 7 видно, что наибольшее значение линейного коэффициента корреляции с зависимой переменной y принадлежит фактору Расходы на рекламу –
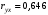 . Поэтому именно этот доминирующий фактор будем использовать для построения уравнения парной линейной регрессии.
. Поэтому именно этот доминирующий фактор будем использовать для построения уравнения парной линейной регрессии.-
Для построения корреляционного поля (или диаграммы рассеяния) используем Мастер диаграмм MS Excel. Для этого выделим «мышью» исходные наблюдения переменных x и y, затем в Главном меню MS Excel выберем: Вставка – Диаграммы – Точечная – Точечная с маркерами. Полученная диаграмма рассеяния представлена на рисунке 8.

Рис. 8. Диаграмма рассеяния в MS Excel
Вывод 1: Как видно из рисунка 8, наблюдается прямая умеренная взаимосвязь между ценой за квартиру (y) и общей площадью (x). Точки на графике сосредоточены вокруг прямой линии, поэтому взаимосвязь ценой за квартиру и общей площадью уместно аппроксимировать прямой линией и применить линейную регрессию с одной объясняющей переменной.
-
Чтобы сформировать расчетную таблицу (последовательно выполняя пункты 3-12 лабораторной работы), необходимо использовать Мастер формул MS Excel (таблица 1). В данном пункте достаточно заполнить столбцы x, y, xy, x2, y2.
Таблица 1
Подготовка данных для оценивания линейной регрессии объема продаж в зависимости от расходов на рекламу
| № п/п | x | y | xy | x2 | y2 | 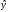 | 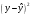 | 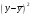 | 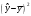 |  |
| 1 | 4 | 126 | 504 | 16 | 15876 | 235,22 | 11928,89 | 32693,16 | 5125,56 | 0,87 |
| 2 | 4,8 | 137 | 657,6 | 23,04 | 18769 | 246,04 | 11889,44 | 28836,29 | 3693,45 | 0,80 |
| 3 | 3,8 | 148 | 562,4 | 14,44 | 21904 | 232,51 | 7142,72 | 25221,41 | 5520,17 | 0,57 |
| 4 | 8,7 | 191 | 1661,7 | 75,69 | 36481 | 298,78 | 11617,09 | 13412,54 | 64,48 | 0,56 |
| 5 | 8,2 | 274 | 2246,8 | 67,24 | 75076 | 292,02 | 324,74 | 1076,66 | 218,80 | 0,07 |
| 6 | 9,7 | 370 | 3589 | 94,09 | 136900 | 312,31 | 3328,52 | 3992,66 | 30,19 | 0,16 |
| 7 | 14,7 | 432 | 6350,4 | 216,09 | 186624 | 379,93 | 2711,60 | 15671,91 | 5345,73 | 0,12 |
| 8 | 18,7 | 445 | 8321,5 | 349,69 | 198025 | 434,02 | 120,49 | 19095,79 | 16182,58 | 0,02 |
| 9 | 19,8 | 367 | 7266,6 | 392,04 | 134689 | 448,90 | 6707,57 | 3622,54 | 20188,79 | 0,22 |
| 10 | 10,6 | 367 | 3890,2 | 112,36 | 134689 | 324,48 | 1808,09 | 3622,54 | 312,08 | 0,12 |
| 11 | 8,6 | 321 | 2760,6 | 73,96 | 103041 | 297,43 | 555,54 | 201,29 | 88,03 | 0,07 |
| 12 | 6,5 | 307 | 1995,5 | 42,25 | 94249 | 269,03 | 1441,75 | 0,04 | 1427,55 | 0,12 |
| 13 | 12,6 | 331 | 4170,6 | 158,76 | 109561 | 351,53 | 421,34 | 585,04 | 1999,34 | 0,06 |
| 14 | 6,5 | 345 | 2242,5 | 42,25 | 119025 | 269,03 | 5771,50 | 1458,29 | 1427,55 | 0,22 |
| 15 | 5,8 | 364 | 2111,2 | 33,64 | 132496 | 259,56 | 10907,13 | 3270,41 | 2232,54 | 0,29 |
| 16 | 5,7 | 384 | 2188,8 | 32,49 | 147456 | 258,21 | 15823,03 | 5957,91 | 2362,17 | 0,33 |
| Сумма | 148,7 | 4909 | | | | | 92499,43 | 158718,44 | 66219,00 | 4,60 |
| Среднее | 9,29 | 306,81 | 3157,46 | 109,00 | 104053,8 | | RSS | TSS | ESS | |
-
Суммы и средние по столбцам в таблице 1 необходимо определить с помощью функций СУММ(…) и СРЗНАЧ(…). -
Оценки коэффициентов модели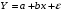 необходимо определить «вручную» ниже таблицы 1, используя ссылки на необходимые ячейки согласно формулам метода наименьших квадратов:
необходимо определить «вручную» ниже таблицы 1, используя ссылки на необходимые ячейки согласно формулам метода наименьших квадратов: 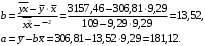
Вывод 2: Запишем модель линейной регрессии:
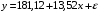 . Экономическая интерпретация коэффициентов следующая. Увеличение расходов на рекламу (х) на 1 тыс. рублей приводит при прочих равных условиях к увеличению объема продаж (y) в среднем на 13,52 тыс. рублей. Данный результат согласуется с экономической интуицией, так как при росте расходов на рекламу можно ожидать увеличения объема продаж. При отсутствии расходов на рекламу объем продаж может составить 181,12 тыс. руб.
. Экономическая интерпретация коэффициентов следующая. Увеличение расходов на рекламу (х) на 1 тыс. рублей приводит при прочих равных условиях к увеличению объема продаж (y) в среднем на 13,52 тыс. рублей. Данный результат согласуется с экономической интуицией, так как при росте расходов на рекламу можно ожидать увеличения объема продаж. При отсутствии расходов на рекламу объем продаж может составить 181,12 тыс. руб.-
Значения дисперсий для x и y, а также средних квадратических отклонений x, y необходимо определить «вручную» ниже таблицы, используя ссылки на необходимые ячейки согласно формулам: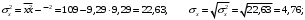
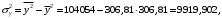
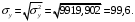 Необходимо проверить результаты с помощью функций ДИСПР(…) и СТАНДОТКЛОНП(…).
Необходимо проверить результаты с помощью функций ДИСПР(…) и СТАНДОТКЛОНП(…). -
Значение линейного коэффициента парной корреляции необходимо определить «вручную» ниже таблицы 1, используя ссылки на необходимые ячейки согласно формуле: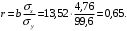 Необходимо проверить результат с помощью функции КОРРЕЛ(…).
Необходимо проверить результат с помощью функции КОРРЕЛ(…).
Вывод 3: Согласно шкале Чеддока-Снедекора наблюдается умеренная прямая статистическая взаимосвязь между объемом продаж и расходами на рекламу.
-
Значение среднего коэффициента эластичности необходимо определить «вручную» ниже таблицы 1, используя ссылки на необходимые ячейки согласно формуле: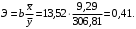
Вывод 4: Увеличение расходов на рекламу на 1 % приводит к увеличению объема продаж на 0,41%.
-
Чтобы вычислить предсказанные моделью значения в таблице 1, необходимо в уравнение регрессии
в таблице 1, необходимо в уравнение регрессии 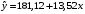 вместо x последовательно, начиная с первого, подставить наблюдаемые значения расходов на рекламу из таблицы 1. Полученные предсказанные моделью значения
вместо x последовательно, начиная с первого, подставить наблюдаемые значения расходов на рекламу из таблицы 1. Полученные предсказанные моделью значения  указать в соответствующем столбце таблицы 1.
указать в соответствующем столбце таблицы 1. -
Остаток регрессии – это ошибка, несвязка (discrepancy) между наблюдаемым значением зависимой переменной yi и предсказанными моделью значениями . Чтобы вычислить остатки регрессии и их квадраты в таблице 1 необходимо заполнить столбец:
. Чтобы вычислить остатки регрессии и их квадраты в таблице 1 необходимо заполнить столбец: 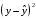 .
. -
Необходимо заполнить в таблице 1 столбцы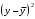 ,
, 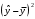 .
. -
Чтобы вычислить суммы квадратов отклонений (TSS, ESS, RSS), необходимо в таблице 1 в строке сумма применить функцию СУММ(…)к столбцам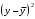 ,
, 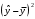 ,
, 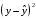 .
.
Чтобы вычислить дисперсии на 1 степень свободы, надо использовать ссылки на необходимые ячейки согласно формулам:
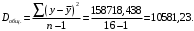
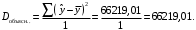
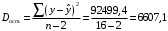
-
Необходимо ниже таблицы 1 проверить балансовое соотношение для суммы квадратов отклонений:
-
Значения коэффициента детерминации и индекса корреляции необходимо определить «вручную» ниже таблицы, используя ссылки на необходимые ячейки согласно формулам: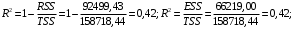
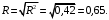
Проверить с использованием коэффициента корреляции
 и с помощью функции КВПИРСОН(…).
и с помощью функции КВПИРСОН(…).Вывод 5: Доля дисперсии объема продаж, объясненная с помощью расходов на рекламу, составляет 42%. Чем ближе R2 к 1, тем лучше качество подгонки регрессии.
-
Чтобы рассчитать стандартную ошибку коэффициента регрессии и значение статистики Стьюдента, необходимо использовать ссылки на необходимые ячейки согласно формулам:
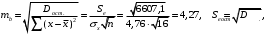
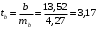 .
.-
Для нахождения критического значения статистики Стьюдента удобно использовать функцию СТЬЮДРАСПОБР(…). В Главном меню MS Excel выберем: Формулы – Вставить функцию – Полный алфавитный перечень – СТЬЮДРАСПОБР(…) (рис. 9).

Рис. 9. Диалоговое окно функции СТЬЮДРАСПОБР(…).
Вывод 6: Поскольку 3,17 > 2,98, то гипотеза Н0: β = 0 отвергается, т.е. согласно тесту Стьюдента коэффициент регрессии β является значимым. Это означает, что между переменными x (расходы на рекламу) и y (объем продаж) существует значимая линейная связь.
-
Чтобы построить доверительный интервал для коэффициента регрессии на уровне значимости 0,01, необходимо, используя ссылки на необходимые ячейки, применить формулу:
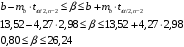
Вывод 7: Диапазон границ доверительного интервала для коэффициента регрессии в модели с хорошим качеством подгонки обычно не превышает 3. В нашем случае, правая граница больше, чем левая, более чем в 3 раза, значит, качество подгонки модели рекомендуется улучшать.