Файл: Лабораторная работа 4 Исследование резонансных явлений в последовательной rlc цепи.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 24
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лабораторная работа № 4
Исследование резонансных явлений
в последовательной RLC-цепи
Цель работы:исследование реакции колебательного контура из
последовательно соединенных RLC-элементов на изменение частоты приложенного синусоидального напряжения с неизменной амплитудой, получение навыков экспериментального исследования резонансных и частотных характеристик, закрепление и расширение знаний о резонансе напряжения.
Выполнение
1. В среде программы NI Multisim соберём схему (Рис 1)
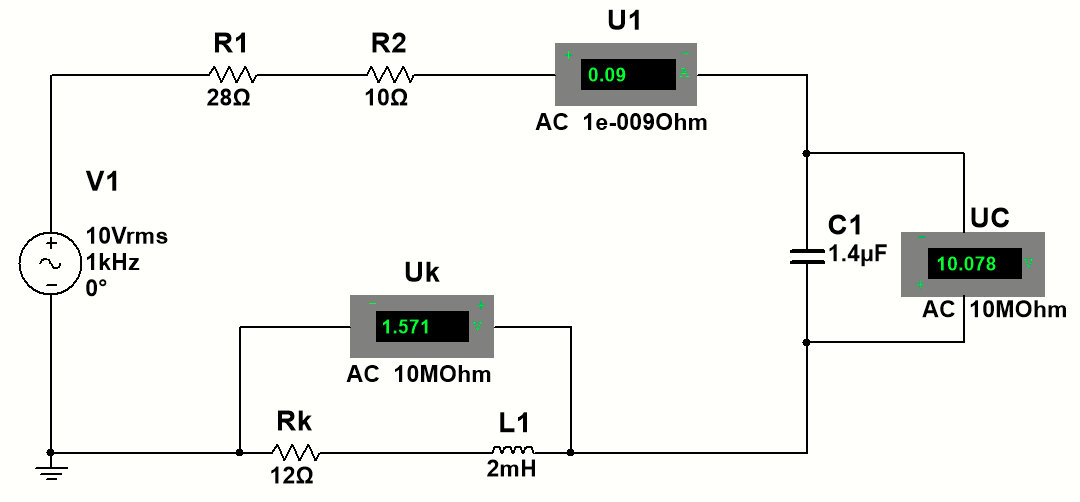
Рис 1
2. Измерим с параметры элементов схемы.
Дано
U=10 В
R1=28 Ом
R2=10 Ом
L1=2 мГн
С1=1,4 мкФ
С2=0,259 мкФ
RК=12 Ом
3. Выставим на звуковом генераторе V1 напряжение 10 В
4. Проведём измерение тока исследуемой цепи I, напряжения UC на емкости и на реальной катушке индуктивности Uк при изменении частоты в диапазоне 1−10 кГц с шагом 1 кГц и занесём результаты измерений в таблицу 1
5. По измеренным данным найдём частоту, при которой наблюдается наибольший ток. Постепенно уменьшая шаг изменения частоты генератора до 10−5 Гц в области этой частоты, определим значение резонансной частоты f0.
Включим вместо конденсатора C1 конденсатор C2 и повторим этапы эксперимента (Рис 2). Данные измерений также внесём в таблицу 1
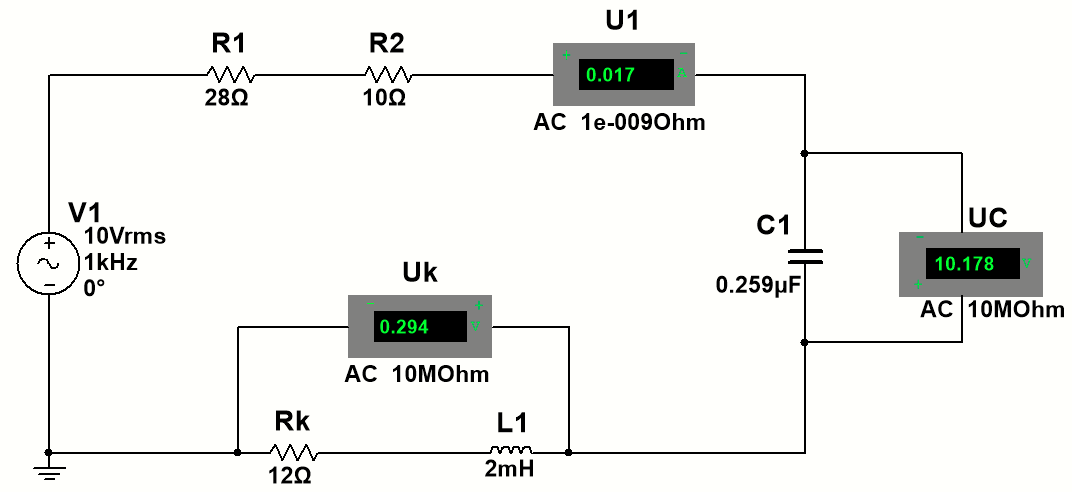
Рис 2
| С | f, кГц | Измерено | Вычислено | |||||||||
| UBX, B | I, ma | UC, B | UK, B | UL, B | XL, B | XC, Ом | Z, Ом | ХЭ, Ом | φ, гр | |||
| С1 | 1 | 10 | 90 | 10,1 | 1,57 | 1,14 | 12,66 | 112,2 | 111,1 | -99,6 | -62,3 | |
| 2 | 10 | 171 | 9,57 | 4,80 | 4,34 | 25,38 | 55,97 | 58,48 | -30,6 | -31,5 | ||
| 3 | 10 | 200 | 7,48 | 8,01 | 7,48 | 38,21 | 38,21 | 50 | 0,0 | 0,0 | ||
| 4 | 10 | 182 | 5,10 | 9,52 | 9,27 | 50,91 | 28,02 | 54,95 | 22,9 | 24,6 | ||
| 5 | 10 | 154 | 3,46 | 10,0 | 9,83 | 63,82 | 22,47 | 64,94 | 41,35 | 39,6 | ||
| 6 | 10 | 131 | 2,45 | 10,1 | 9,98 | 76,16 | 18,70 | 76,34 | 57,46 | 49,0 | ||
| 7 | 10 | 113 | 1,81 | 10,2 | 10,1 | 89,46 | 16,02 | 88,50 | 73,45 | 55,8 | ||
| 8 | 10 | 99 | 1,39 | 10,1 | 10,1 | 102,3 | 14,04 | 101,0 | 88,29 | 60,5 | ||
| 9 | 10 | 88 | 1,10 | 10,1 | 10,0 | 114,1 | 12,50 | 113,6 | 101,6 | 63,8 | ||
| 10 | 10 | 79 | 0,89 | 10,1 | 10,0 | 127,3 | 11,27 | 126,6 | 116,0 | 66,7 | ||
| f0 | 10 | 200 | 7,48 | 8,01 | 7,48 | 38,21 | 38,21 | 50 | 0,0 | 0,0 | ||
| С2 | 1 | 10 | 17 | 10,2 | 0,29 | 0,206 | 12,12 | 600,0 | 588,2 | -588 | -85,2 | |
| 2 | 10 | 35 | 10,7 | 1,00 | 0,908 | 25,93 | 305,7 | 285,7 | -280 | -79,9 | ||
| 3 | 10 | 58 | 11,8 | 2,34 | 2,234 | 38,52 | 203,4 | 172,4 | -165 | -73,2 | ||
| 4 | 10 | 89 | 13,5 | 4,65 | 4,526 | 50,85 | 151,7 | 112,4 | -101 | -63,7 | ||
| 5 | 10 | 131 | 15,9 | 8,49 | 8,343 | 63,69 | 121,4 | 76,34 | -57,7 | -49,1 | ||
| 6 | 10 | 179 | 18,1 | 13,9 | 13,73 | 76,72 | 101,1 | 55,87 | -24,4 | -26,0 | ||
| 7 | 10 | 200 | 17,3 | 18,0 | 17,3 | 88,2 | 88,2 | 50 | 0,0 | 0,0 | ||
| 8 | 10 | 177 | 13,5 | 18,2 | 18,08 | 102,1 | 76,27 | 56,5 | 25,9 | 27,4 | ||
| 9 | 10 | 145 | 9,80 | 18,8 | 18,72 | 129,1 | 67,59 | 68,97 | 61,5 | 50,9 | ||
| 10 | 10 | 120 | 7,28 | 15,3 | 15,23 | 126,9 | 60,67 | 83,33 | 66,27 | 53,0 | ||
| f0 | 10 | 200 | 17,3 | 18,0 | 17,3 | 88,2 | 88,2 | 50 | 0,0 | 0,0 | ||
Используя данные измерений, внесенные в таблицу 1, рассчитаем индуктивную составляющую напряжения реальной катушки индуктивности UL и ее индуктивное сопротивление XL. Определить емкостное сопротивление XC, эквивалентное реактивное сопротивление XЭ, полное сопротивление цепи Z, угол сдвига фаз между током и напряжением, добротность Q и полосу пропускания резонансного контура.
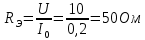
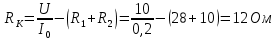
Индуктивную составляющую напряжения реальной катушки UL можно вычислить по следующей формуле (4.5)
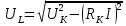
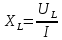
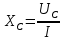
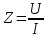
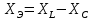
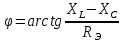
Используя эти формулы произведём расчёты для конденсатора С1 и при частоте f = 1 кГц
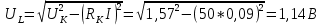
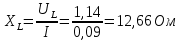
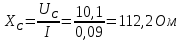
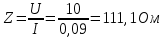
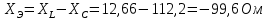
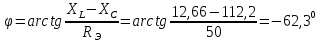
Аналогично произведём расчёты и для других частот и результаты внесём в таблицу 1
Добротность контура можно определить при резонансе для С1
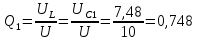
Добротность контура можно определить при резонансе для С1
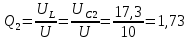
Скопируем осциллограммы при частотах до резонанса, при резонансе и после резонанса
Используя данные таблицы построим в масштабе векторные диаграммы для частот f = 1 кГц, f0 = 3 кГц, f = 5 кГц,
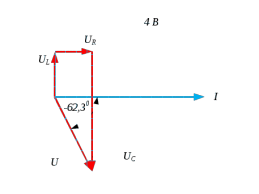
Рис 3 Векторная диаграмма тока и напряжений для режима f=1 кГц
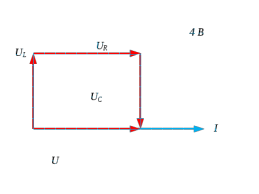
Рис 4 Векторная диаграмма тока и напряжений для режима f=3 кГц
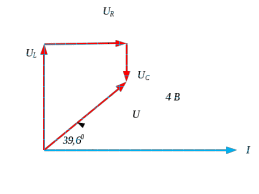
Рис 5 Векторная диаграмма тока и напряжений для режима f=5 кГц
В среде программы Mathcad снимем зависимости параметров схемы от частоты
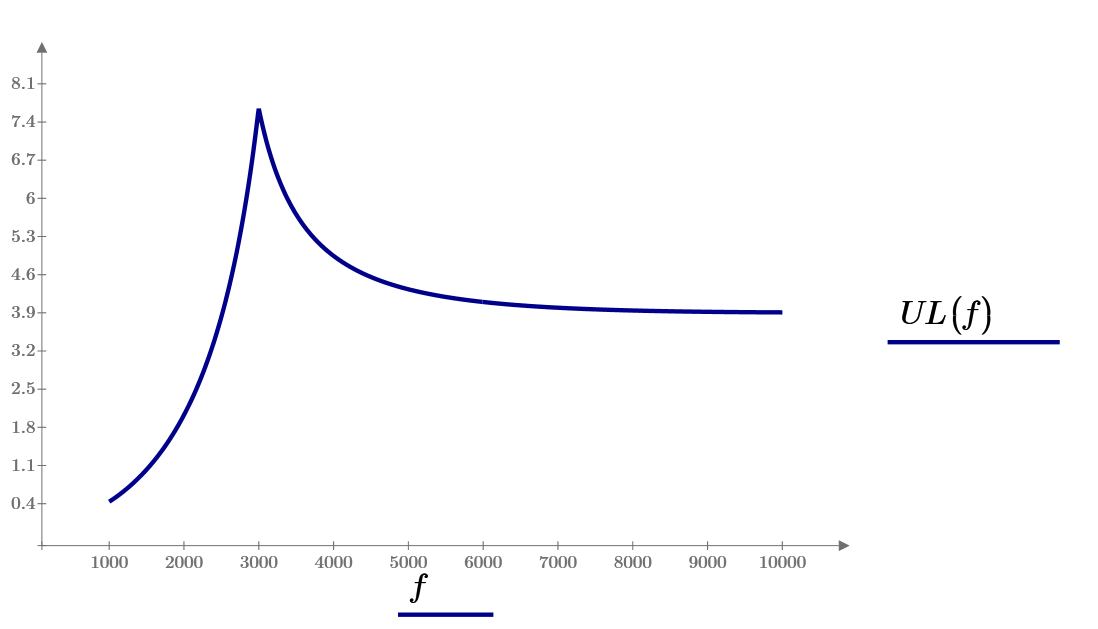
Рис 6 Зависимость напряжения на индуктивности от частоты
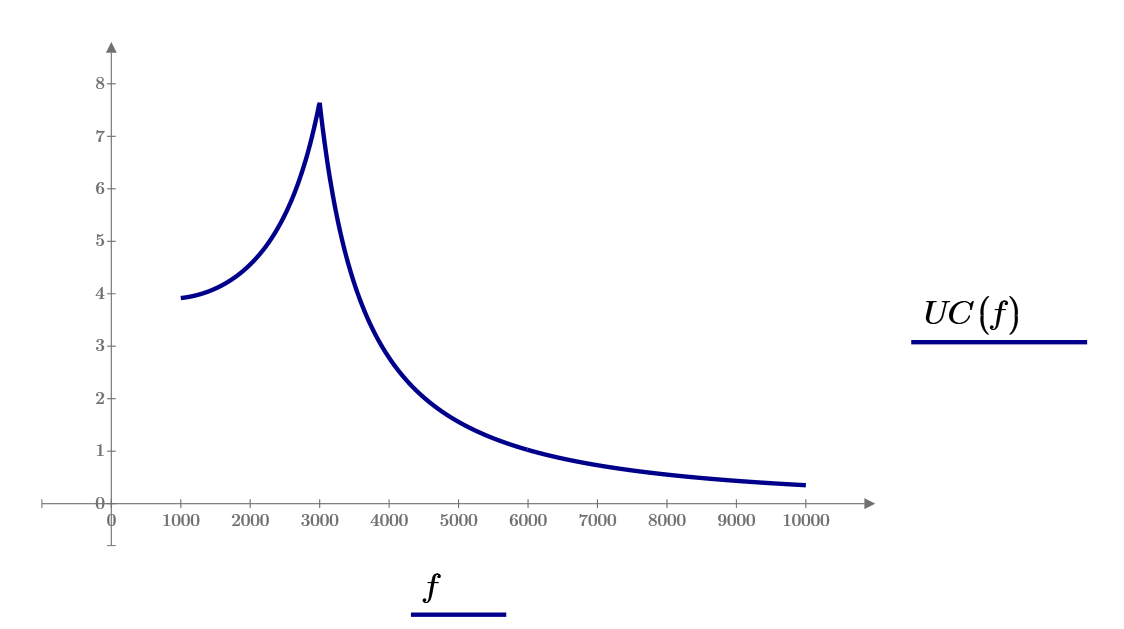
Рис 7 Зависимость напряжения на ёмкости от частоты
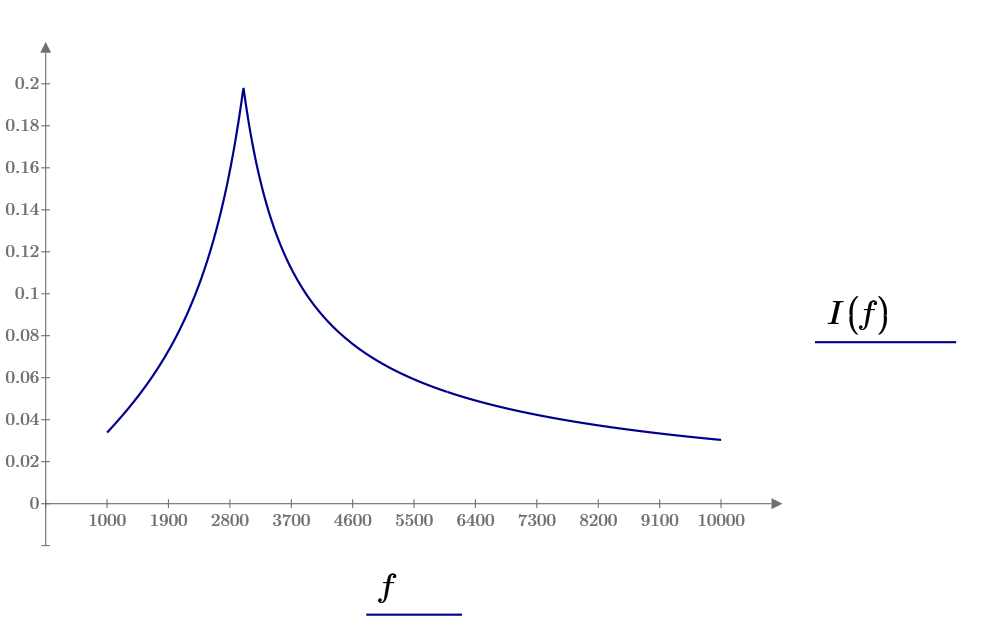
Рис 8 Зависимость величины тока от частоты
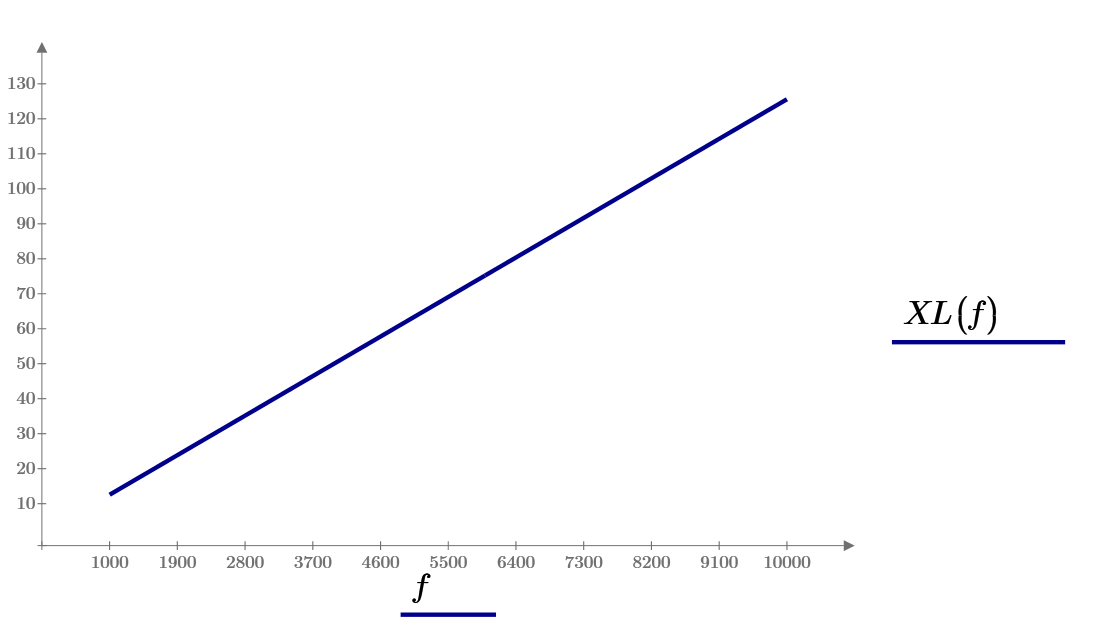
Рис 9 Зависимость сопротивления индуктивности от частоты
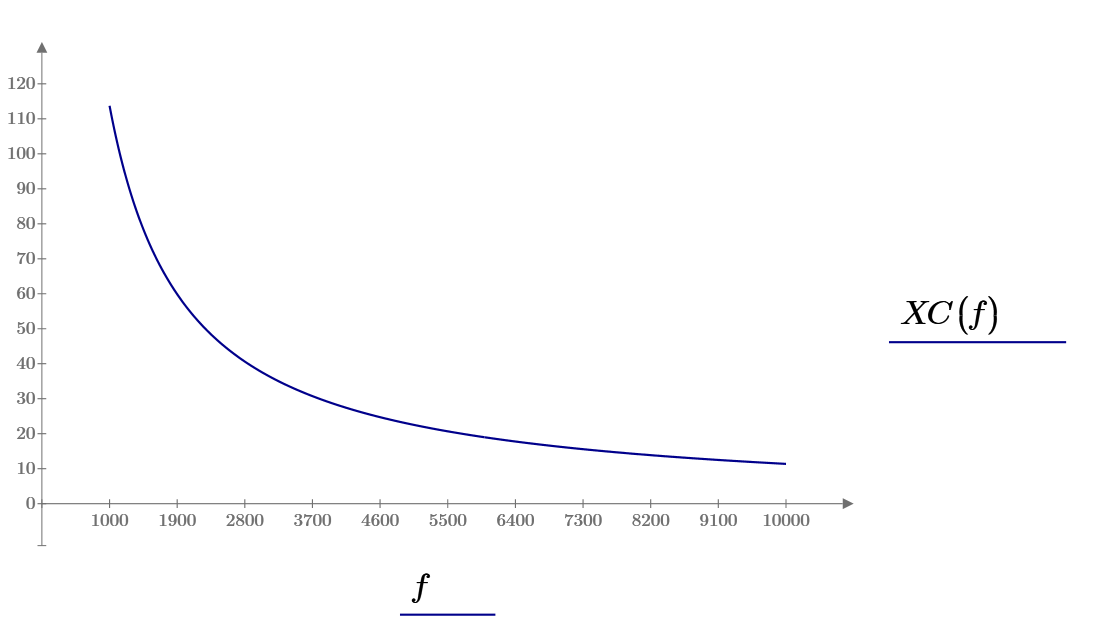
Рис 10 Зависимость сопротивления конденсатора от частоты
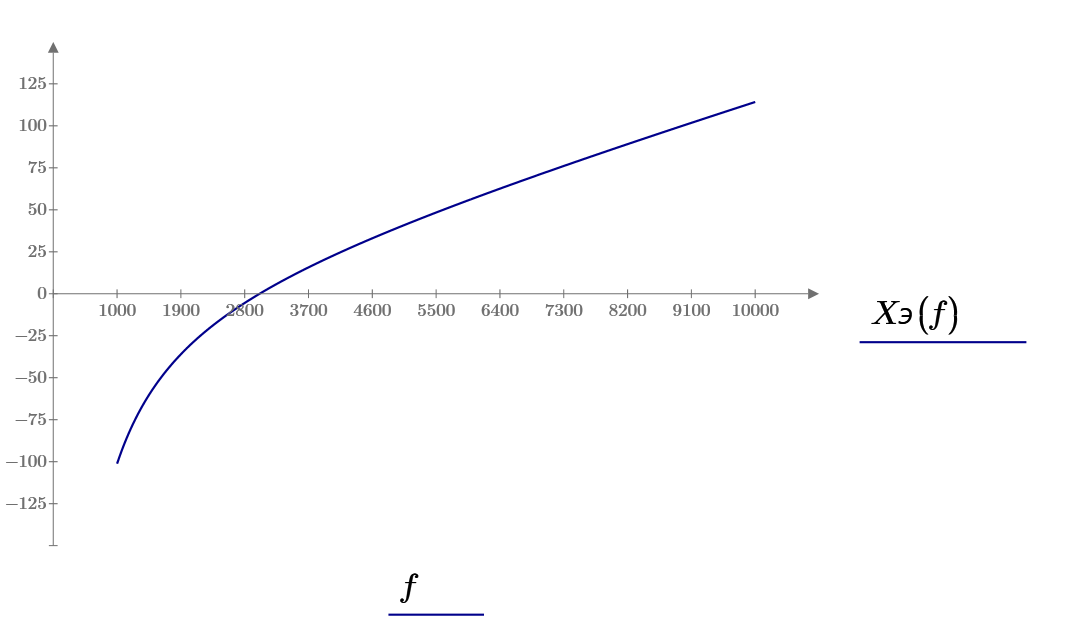
Рис 11 Зависимость величины реактивного сопротивления от частоты
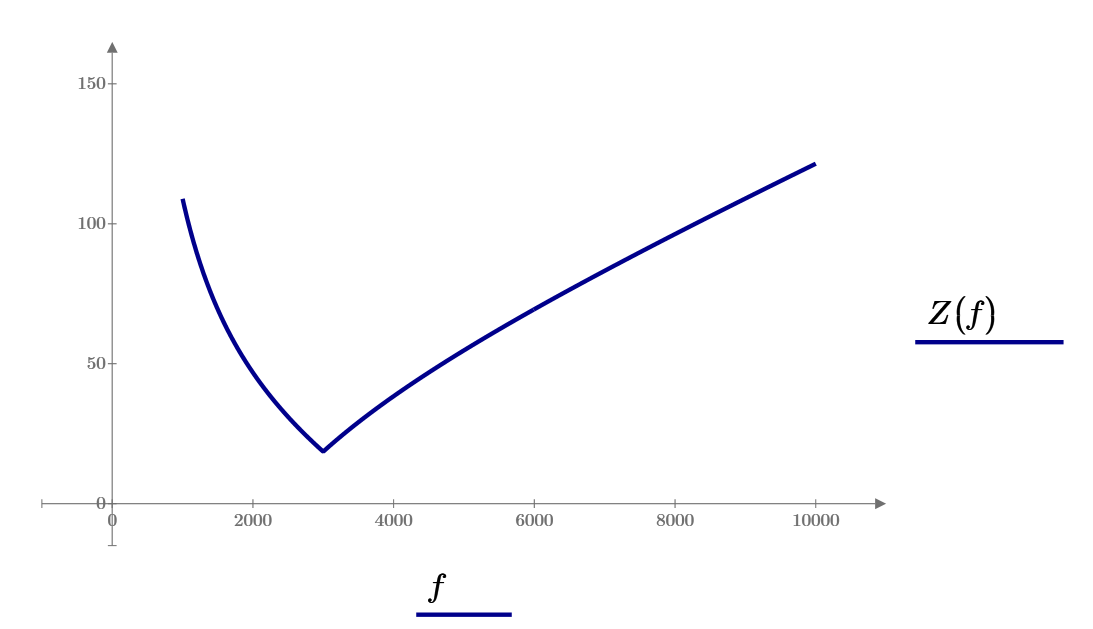
Рис 12 Зависимость величины входного сопротивления от частоты
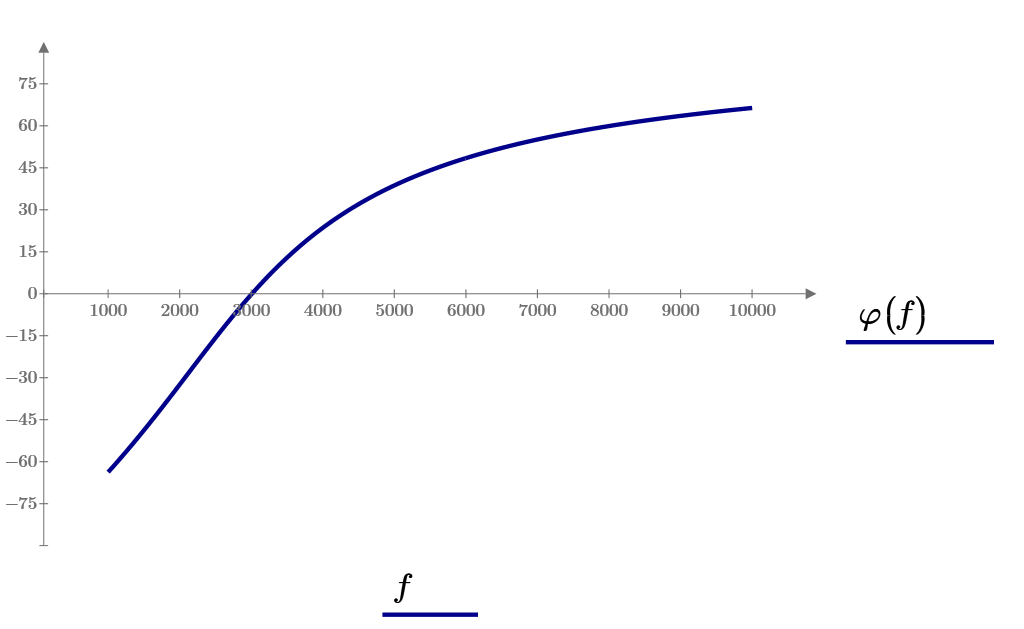
Рис 13 Зависимость угла между векторами тока и напряжения от частоты
ОТВЕТЫ НА ВОПРОСЫ
Резонансом называют такой режим работы пассивной цепи, при котором входной ток совпадает по фазе с входным напряжением, несмотря на наличие в цепи реактивных элементов.
Если цепь представляет собой последовательное соединение двухполюсников, содержащих реактивные элементы разного характера, то возникновение резонанса объясняется взаимной компенсацией реактивных составляющих напряжений на этих двухполюсниках. В этом случае говорят о резонансе напряжений.
В этой схеме резонанса можно добиться,
изменяя либо частоту, либо индуктивность, либо емкость.
; 
, 
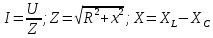
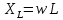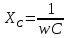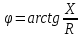
Ток совпадает по фазе с напряжением (
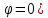при условии х = 0, т.е. при 
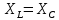или ????2LC = 1.Если активное сопротивление цепи невелико, то ток в цепи резко возрастает по сравнению с входным током, так как реактивное сопротивление цепи становится равным нулю.
Когда ток I совпадает по фазе с напряжением U и
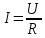, Резкое возрастание тока в цепи при резонансе напряжений вызывает такое же возрастание напряжений
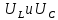, причем их значения могут во много раз превышать напряжение U источника, питающего цепь.По результатам измерений можно определить параметры катушки индуктивности:
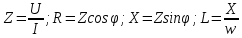
Резонансная емкость:
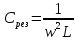
Качественные векторные диаграммы (Рис 3, 4, 5)
Если емкость больше резонансной (С >C рез), то угол сдвига фаз имеет знак «+».
Если емкость меньше резонансной (С <Срез), то угол сдвига фаз имеет знак «-».
Выводы
Если собрать цепь из последовательно соединенных емкости и индуктивности и подключить ее к источнику переменного напряжения, то в этой цепи может наступить резонанс напряжений. Этот резонанс наступает при равенстве емкостного и индуктивного сопротивлений. Используя явление резонанса можно определить параметры или катушки или конденсатора. Для этого необходимо знать частоту переменного напряжения и параметры одного реактивного элемента. Если в цепи сопротивление индуктивности больше емкостного сопротивления, то в этой цепи ток будет отставать от приложенного напряжения, а если реактивное сопротивление конденсатора будет больше реактивного сопротивления индуктивности, то в этой цепи ток будет опережать приложенное напряжение.