Найдем микропервеанс одного электронного луча:

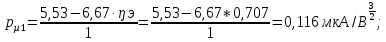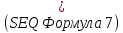Выходная мощность связана с параметрами электронного потока соотношением:

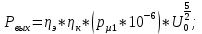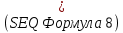Из уравнения (8) получаем аналитическое выражение для определения ускоряющего напряжения:

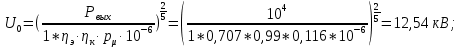Исходя из полученных расчетных данных можно определить подводимую мощность и ток пучка:



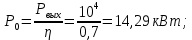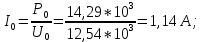2.3 Расчет скорости электронного пучка

Скорость электронного пучка определяется выражением:

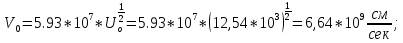Выбор угла пролета по радиусу пролетного канала 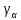на высоких частотах ограничен до одномодового режима следующим уравнением:

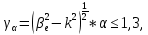где 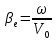– электронная постоянная распространения, 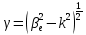– радиальное волновое число,

---

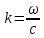– волновое число, 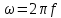– угловая частота, 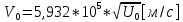– скорость электронов.

Выбор 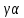определяется рядом противоречивых условий. С одной стороны, его уменьшение приводит к повышению эффективности процесса взаимодействия. С другой – возрастает величина магнитного поля и плотность тока в пучке. На очень высоких частотах возникает также проблема изготовления пролетных каналов малого диаметра. Зависимость этого параметра от частоты, наблюдаемую на практике для МЛК, можно описать следующим приближенным выражением:

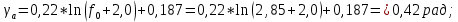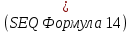Выберем диаметр пучка, учитывая, что пропорционально уменьшению диаметра пролетного канала 2a увеличивается сходимость по радиусу электронного потока, что в свою очередь ставит ограничение на максимально допустимый первеанс электронной пушки. Выбираем угол пролета по радиусу пролетного канала 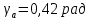. Ищем радиус пролетного канала:

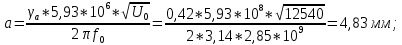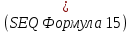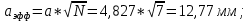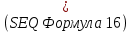Выбираем коэффициент заполнения пролетного канала пучком 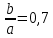. Находим угол пролета по радиусу пролетного канала :

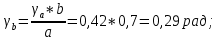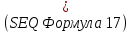В квазистационарном резонаторе почти вся энергия электрического поля сосредоточена в одной (обычно небольшой по сравнению с длиной волны) емкостной части резонатора, а энергия магнитного поля – в другой (индуктивной) части резонатора.

---

Для эффективного взаимодействия с пучком бессеточный зазор должен быть довольно коротким при этом длина силовых линий энергетического поля сокращается, что эквивалентно увеличению ёмкости зазора. С точки зрения снижения ВЧ потерь в резонаторе необходимо уменьшение ёмкости зазора. Поэтому пролетные трубы часто выполняют с «тонкими» стенками. Для этого концы пролетных труб выполняют в виде конических цилиндров.

Задаем относительную длину зазора выходного резонатора .

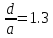Теперь находим угол пролетного зазора и длину зазора:

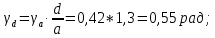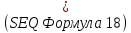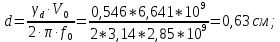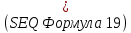Найдем длину втулки. Примем отношение 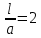. Отсюда найдем l:



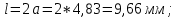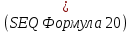2.4 Расчет в программе REZ-1

Зная параметры резонатора, воспользуемся программой REZ-1. Данная программа используется для первого приближения. Программа предоставляет картину резонатора с геометрическими размерами, а также высчитанные параметры (Рис. 2).



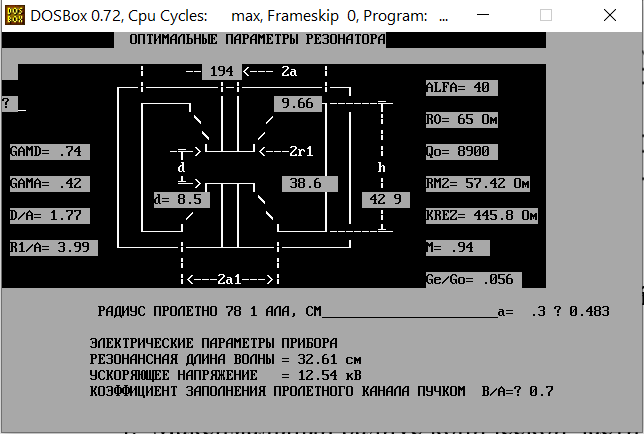
Рис. 2 Оптимальные параметры резонатора
2.5 Расчет в программе Azimut

Зная примерные размеры резонатора, воспользуемся программой Azimut. Задаем координаты участков границы (Рис. 3) до тех пор, пока не получим нужную частоту. Далее определим основные размеры резонатора (Рис. 4), получим собственную частоту и параметры резонатора при типе колебаний (Рис. 5), картину электрического поля при типе колебаний

---

(Рис. 6), распространение поля в объёме резонатора при типе колебаний (Рис. 7).



Рис. 3 Координаты участков границы резонатора



Рис. 4 Контур резонатора



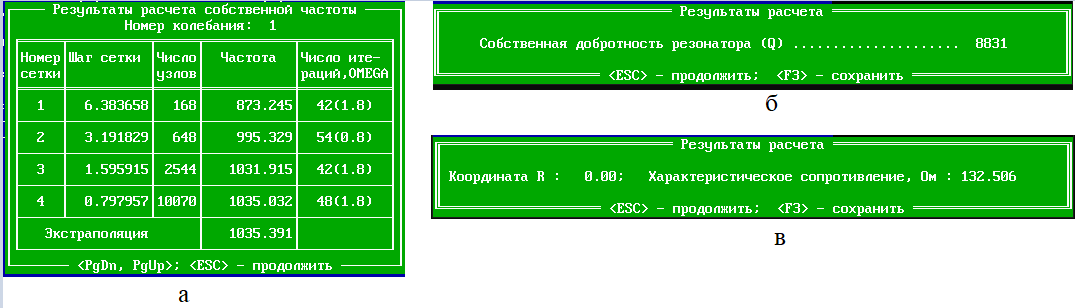
Рис. 5 Параметры резонатора при типе колебаний : а) собственная частота; б) собственная добротность; в) характеристическое сопротивление.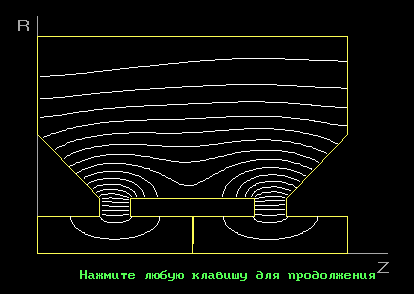



Рис. 6 Картина электрического поля при типе колебаний .



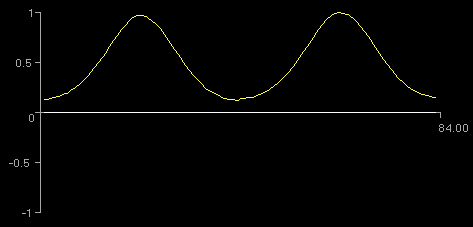
Рис. 7 Распространение поля в объёме резонатора при типе колебаний .



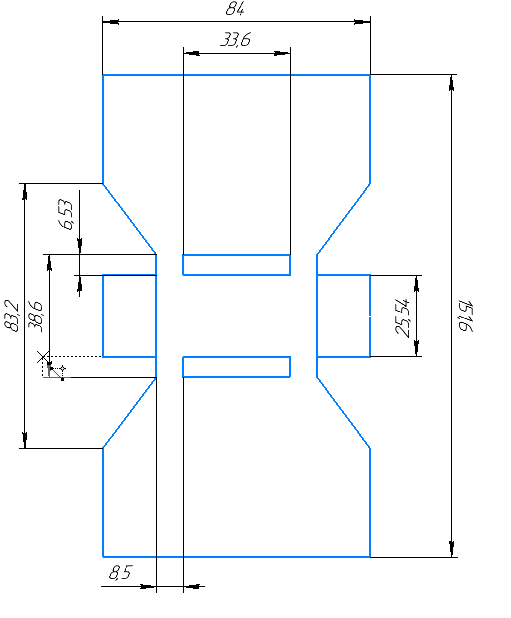
Рис. 8 Оптимальные размеры резонатора.

Таблица 2. Результаты расчета промежуточного резонатора.

Параметр	Значение
Внешний диаметр резонатора, мм	151,6
Диаметр широкой части «трапеции», мм	83,2
Диаметр узкой части «трапеции», мм	38,6
Диаметр пролетного канала, мм	25,54
Длина электрода, мм	33,6
Высота электрода, мм	6,53
Длина зазора, мм	8,5
Внутренняя ширина резонатора	84
Собственная добротность резонатора	8831
Резонасная длина волны, см	32,61
Ускоряющее напряжение, кВ	12,54
Коэффициент заполнения канала пучком	0,7
Угол пролета зазора 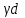,рад	0,55
Угол пролета по радиусу канала 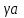,рад	0,42
Отношение длины зазора и радиуса пролетного канала d/a	1,3
Пролетный радиус r1/a	3,99
Характеристическое сопротивление ρ, Ом	132,586
Коэффициент взаимодействия, М	0,94
Активная проводимость Ge/G0	0,056
Коэффициент качества Ккач, Ом	445,5

---

2.6 Расчет параметров выходного резонатора в программе DISKLY

(с учетом взаимодействия)

На этом этапе воспользуемся ранее полученными данными и осуществим вычисления в программе Diskly. Выставленные параметры представлены в таблице 3 и на рис. 9.


Таблица 3. Данные выставленные в DISKLY.

Исходные данные
№ Резонатора	1	2	3	4	5
IR	1	1	1	1	1
KF	1	1	1	1	1
Z	0	84	168	252	336
GES	0.056	0.056	0.056	0.056	0.056
BES	0.01	0.01	0.01	0.01	0.01
AMS	0.94	0.94	0.94	0.94	0.94
ROS	928	928	928	928	928
QS	4415	8831	8831	8831	31
DFS	0	895	915	935	0
Данные для оптимизации
X	0	900	915	925	0
WERR	0	2	4	8	16

---

Смотрите также файлы

• Внеклассное чтение По страницам басен А. И. Крылова (5 класс) Цели урока Регулятивные способность участвовать в речевом общении.pptx

• С оценкой 20г 20г тема работы экономика рыбной отрасли Канады. Курсовая работа по дисциплине Мировой рыбный рынок.docx

• Контрольная работа по географии За 20212022 учебный год Ученика (цы) 5 (А,Б) класса.docx

• Основная задача.docx

• Название материала.docx