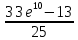Файл: Внимание! Данное задание необходимо выполнить и отправить на проверку преподавателю. Задание.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 21
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Внимание! Данное задание необходимо выполнить и отправить на проверку преподавателю.
Задание. Для функции ???? = (2???? + 3)????5???? :
-
Найти область определения, точки разрыва. -
Исследовать функцию на четность, периодичность. -
Исследовать поведение функции на концах области определения. Указать асимптоты. -
Найти промежутки монотонности. Точки экстремума. -
Найти промежутки выпуклости. Точки перегиба. -
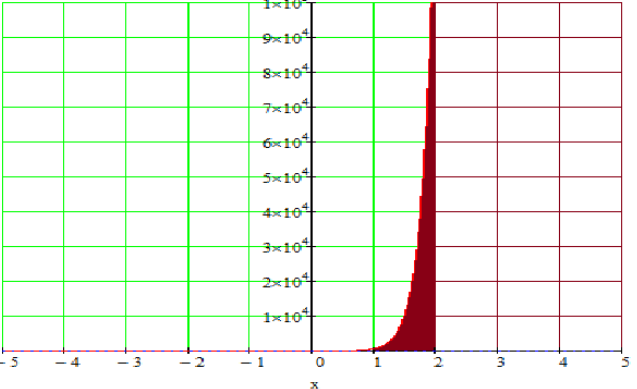
Найти площадь фигуры, ограниченной графиком функции
???? = (2???? + 3)????5???? и прямыми ???? = 0, ???? = 2, ???? = 0.
Результаты исследования оформить в виде таблицы.
| Область определения: | D(y) = R |
| Четность, периодичность: | Ни четная, ни нечетная. Функция непериодическая |
| Поведение на концах области определения: | Точка пересечения с Ох -3/2 Точка пересечения с Оу (0,3) |
| Асимптоты: | 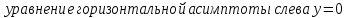 горизонтальной асимптоты справа и наклонных не существует |
| Промежутки монотонности: | функция убывает на промежутке [-17/10 , 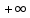 ) )функция возрастает на промежутке ( - 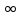 , - 17/10 ] , - 17/10 ] |
| Точки экстремума: | Минимум функции в точке (- 17/10) Максимум функции отсутствует |
| Промежутки выпуклости: | вогнутая на промежутке [-19/10 , 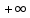 ) ) выпуклая на промежутке ( - 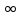 , - 19/10 ] , - 19/10 ] |
| Точки перегиба: | -19/10 - точка перегиба |
| Площадь криволинейной трапеции. | 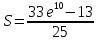 |
1) Область определения функции - вся числовая ось: D(y) = R
2) y=(2x+3)e^5x , y(-x)=(-2x+3)e^(-5x)
y(-x) не равно y(x)
y(-x) не равно -y(x)
Функция не является ни чётной, ни нечётной. Функция не является периодической.
3) Точки пересечения с осью координат Ох.
График функции пересекает ось Ох при f = 0:
(2x+3)e^5x=0
2x+3=0 x= - 3/2
e^5x=0 - решений нет
Точки пересечения с осью координат Оу.
График пересекает ось Oy, когда x равняется 0.
Точка пересечения графика с осью координат Оу соответствует аргументу х = 0.
y=(2*0+3)e^5*0
y=3
(0,3) – точка пересечения с Оу
4) Горизонтальная асимптота
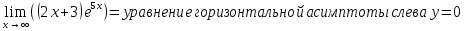
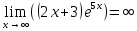 - горизонтальной асимптоты справа не существует
- горизонтальной асимптоты справа не существуетНаклонная асимптота y = kx + b.
Находим коэффициент k:
k=
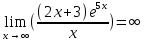
Найдем наклонную асимптоту при x → -∞:
Находим коэффициент k:
k=
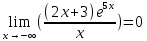
Наклонных асимптот не существует
5,6) Найти промежутки монотонности. Точки экстремума.
y=(2x+3)e^5x
((2·x+3)·e5·x)' = (2·x+3)'·e5·x+(2·x+3)·(e5·x)' = 2·e5·x+(2·x+3)·5·e5·x = 17*e5x + 10*x*e5x
17*e5x + 10*x*e5x = 0
e5x (17+10*x) = 0
(17+10*x) = 0 x = -17/10 минимум функции
e5x – решений нет
функция убывает на промежутке [-17/10 ,+
 )
)функция возрастает на промежутке ( -
 , - 17/10 ]
, - 17/10 ]7,8) Найти промежутки выпуклости. Точки перегиба.
y''=17e^(5x)+10xe^(5x) = 50xe5x+95e5x
50xe5x+95e5x = 0
e5x (50+95x) = 0
(50+95x) = 0 x = -19/10 - точка перегиба
e5x – решений нет
вогнутая на промежутке [-19/10 ,
 ) , выпуклая на промежутке ( -
) , выпуклая на промежутке ( -  , - 19/10 ]
, - 19/10 ]9) Найти площадь фигуры, ограниченной графиком функции
???? = (2???? + 3)????5????
и прямыми ???? = 0, ???? = 2, ???? = 0.
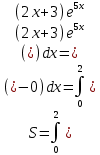
=
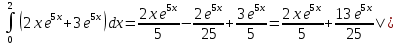 20 =
20 =