Файл: Автоматизация газоперекачивающих агрегатов с газотурбинным приводом компрессорных станций магистральных газопроводов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 279
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- время предварения (постоянная дифференцирования).Таблица 8 - Параметры настройки регуляторов для объектов
без самовыравнивания
| Регулятор | Типовой процесс регулирования | ||
| апериодический | с 20% перерегулированием | ||
| П |  |  | |
| ПИ |  |  | |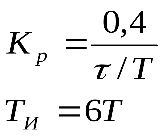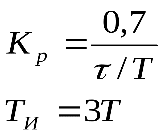
| ПИД |  |  | |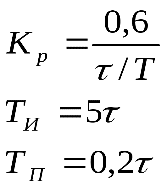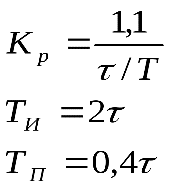
Когда параметры настройки регулятора определены, используя формулу 4, запишем передаточные функцию регулятора.
с учетом типового процесса регулирования
Рассматриваемый объект управления обладает самовыравниванием и аппроксимируется апериодическим звеном 1-го порядка. Исходя из этого, в качестве типового примем апериодический процесс.
Параметры регулятора определим из формулы:
Тогда Kp=5,4; Tи=5,4.
Таким образом, передаточная функция ПИ- регулятора примет вид:
. типового процесса регулирования
Параметры регулятора определим из формул:
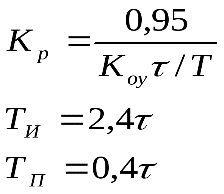
Кр=8,59; Ти=4,8; Тп
=0,8
Тогда передаточная функция ПИ- регулятора примет вид:
. Понятиеустойчивости является важнейшей качественной оценкой динамических свойств САР. Способность системы восстанавливать состояние равновесия, из которого она была выведена в результате какого-либо воздействия, называется устойчивостью. В зависимости от характера переходного процесса различают три основных случая поведения или изменения заданного значения регулируемой величины:
-
если с течением времени после окончания переходного процесса система приходит в первоначальное или другое установившееся состояние, то такой переходный процесс будет сходящимся, а система – устойчивой; -
если при тех же условиях система характеризуется установившимся периодическим движением, то такой переходный процесс называется незатухающим, колебательным, а система находится на границе устойчивости; -
если система не может восстановить равновесного состояния, а значение регулируемой величины всё более отклоняется от заданного, то такой процесс называется расходящимся, а система – неустойчивой.
С целью упрощения анализа устойчивости систем разработано ряд специальных методов, которые получили название критерии устойчивости. Критерии устойчивости делятся на две разновидности: алгебраические и частотные. Алгебраические критерии являются аналитическими, а частотные - графо-аналитическими. Критерии устойчивости позволяют также оценить влияние параметров системы на устойчивость.
Следует обратить внимание на важные преимущества критерия устойчивости Найквиста по сравнению с критериями Раусса – Гурвица и Михайлова:
1. При использовании этого критерия нет необходимости в знании характеристического уравнения замкнутой системы – вся необходимая информация может быть получена экспериментально.
2. Критерий применим для систем с распределенными параметрами и транспортным запаздыванием, передаточные функции которых трансцендентны.
Теорема (критерий Найквиста). Для устойчивости САУ необходимо и достаточно
, чтобы годограф разомкнутой системы
при измененииω от 0 до ∞ охватывал l/2 раз в положительном направлении точку (-1, i0), где l – число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости.Из этой теоремы непосредственно вытекает.
Следствие. Если разомкнутая система устойчива (l=0), то для устойчивости замкнутой системы необходимо и достаточно, чтобы частотный годограф
при измененииω от 0 до ∞ не охватывал точку (-1, i0).Заметим, что для применения частотного критерия устойчивости Найквиста необходимо знать, устойчива или неустойчива система в разомкнутом состоянии. При этом, если система в разомкнутом состоянии неустойчива, то следует определить количество корней её характеристического уравнения, имеющих положительные вещественные части. Только в этом случае можно применить частотный критерий устойчивости Найквиста к исследованию устойчивости замкнутой системы.