Файл: Эмпирическая функция распределения. Полигон и гистограмма. В результате изучения темы студент должен.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 69
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
где – исправленная дисперсия.
– исправленная дисперсия.
Для оценки среднего квадратического отклонения используется величина S, равная квадратному корню из исправленной дисперсии, которая называется исправленным средним квадратическим отклонением.
Рассмотренные оценки характеризуются одним числом и называются точечными.
Пример 1. По заданному статистическому ряду (табл. 1) требуется:
а) построить гистограмму относительных частот;
б) перейти к вариантам и построить полигон относительных частот;
в) построить эмпирическую функцию распределения.
Таблица 1
Решение
а) Объем выборки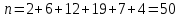 .
.
Определяем относительные частоты и составляем табл. 2 с относительными частотами:
и составляем табл. 2 с относительными частотами:
Таблица 2
Для построения гистограммы относительных частот на оси абсцисс откладываются частичные интервалы длины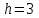 , а над ними проводятся горизонтальные отрезки на расстоянии
, а над ними проводятся горизонтальные отрезки на расстоянии 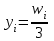 (рис. 1).
(рис. 1).
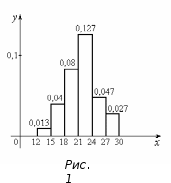
б) Перейдем к вариантам, положив их равными серединам частичных интервалов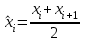 , где
, где 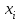 ,
, 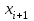 – концы интервалов. Тогда табл. 2 превратится в табл. 3:
– концы интервалов. Тогда табл. 2 превратится в табл. 3:
Таблица 3
Отметим на плоскости точки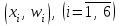 и, соединив соседние точки, получим полигон относительных частот (рис. 2).
и, соединив соседние точки, получим полигон относительных частот (рис. 2).
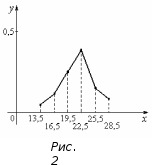
в) Эмпирическая функция распределения строится по закону:
строится по закону:
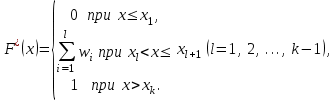
В нашем случае получаем:
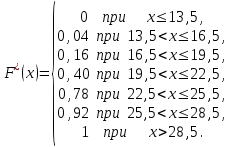
График функции представлен на рис. 3.
представлен на рис. 3.
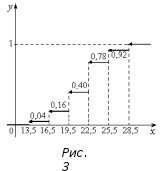
Пример 2.В условиях примера 1 найти статистические оценки.
Решение Обратимся к табл. 3: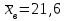 ;
; 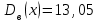 ;
;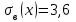 .
.
Контрольные вопросы:
Задачи на закрепление материала
Статистический ряд задан таблицей. Требуется:
а) построить гистограмму относительных частот;
б) перейти к вариантам и построить полигон относительных частот;
в) записать эмпирическую функцию распределения и построить ее график;
г) найти точечные оценки
 ,
, 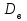 ,
, 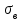 ;
;
Тема лекции: Интервальные оценки параметров распределения
План:
Определение: Интервальнойназывают оценку, которая определяется двумя числами – концами интервала.
Так как любая оценка есть некоторое приближение оцениваемой величины a, то возникает вопрос об оценке точности данного приближения, т. е. можно ли утверждать, что
есть некоторое приближение оцениваемой величины a, то возникает вопрос об оценке точности данного приближения, т. е. можно ли утверждать, что 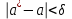 для некоторого
для некоторого 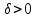 .
.
Однако статистические методы не позволяют категорически утверждать, что оценка удовлетворяет неравенству
удовлетворяет неравенству 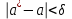 . Можно лишь говорить о вероятности наступления события, заключающегося в том, что мы получили оценку с точностью :
. Можно лишь говорить о вероятности наступления события, заключающегося в том, что мы получили оценку с точностью : 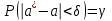 . Эта вероятность называется доверительной вероятностью (или надежностью), а интервал
. Эта вероятность называется доверительной вероятностью (или надежностью), а интервал 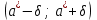 – доверительным интервалом. Вероятность того, что интервал
– доверительным интервалом. Вероятность того, что интервал 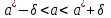 заключает в себе неизвестный параметр a, равна . Обычно надежность выбирают близкой к единице (0,95; 0,99; 0,999).
заключает в себе неизвестный параметр a, равна . Обычно надежность выбирают близкой к единице (0,95; 0,99; 0,999).
Если случайная величина распределена нормально и среднее квадратическое отклонение известно, то доверительный интервал для оценки математического ожидания a
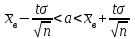 , (1)
, (1)
где n – объем выборки, t находится из равенства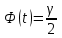 по таблице значений функции Лапласа
по таблице значений функции Лапласа 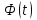 .
.
Если неизвестно, то в формуле (1) оно заменяется на исправленное среднее квадратическое отклонение S, t заменяется на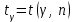 , которое находится по таблице (приложение )
, которое находится по таблице (приложение )
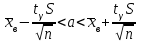 . (2)
. (2)
Доверительный интервал для оценки среднего квадратического отклонения
нормального распределения с заданной надежностью находится по формуле
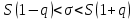 , (3)
, (3)
где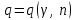 находится по таблице (приложение ).
находится по таблице (приложение ).
Пример 1. Дано распределение частот выборки (табл. 1). Найти доверительные интервалы для математического ожидания a и среднего квадратического отклонения с доверительной вероятностью = 0,95, если известно, что генеральная совокупность распределена по нормальному закону
Таблица 1
Решение
Имеем: ,
, 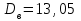 ,
, 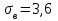 . Так как объем выборки
. Так как объем выборки 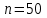 , то находим
, то находим
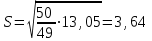 .
.
По таблице приложения находим
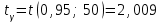 .
.
Подставляя полученные значения S и t в формулу (2), получим
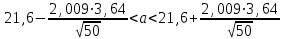
или
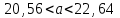 .
.
По таблице приложения найдем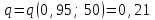 .
.
Подставляя значения S и q в формулу (3), получим
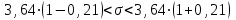
или
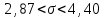 .
.
3.Интервальная оценка вероятности события
Интервальной оценкой (с надежностью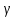 ) неизвестной вероятности р биномиального распределения по относительной частоте
) неизвестной вероятности р биномиального распределения по относительной частоте
где
 – исправленная дисперсия.
– исправленная дисперсия.Для оценки среднего квадратического отклонения используется величина S, равная квадратному корню из исправленной дисперсии, которая называется исправленным средним квадратическим отклонением.
Рассмотренные оценки характеризуются одним числом и называются точечными.
Пример 1. По заданному статистическому ряду (табл. 1) требуется:
а) построить гистограмму относительных частот;
б) перейти к вариантам и построить полигон относительных частот;
в) построить эмпирическую функцию распределения.
Таблица 1
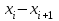 | 12 –15 | 15 – 18 | 18 – 21 | 21 – 24 | 24 – 27 | 27 – 30 |
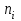 | 2 | 6 | 12 | 19 | 7 | 4 |
Решение
а) Объем выборки
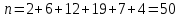 .
.Определяем относительные частоты
 и составляем табл. 2 с относительными частотами:
и составляем табл. 2 с относительными частотами:Таблица 2
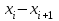 | 12 –15 | 15 – 18 | 18 – 21 | 21 – 24 | 24 – 27 | 27 – 30 |
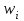 | 0,04 | 0,12 | 0,24 | 0,38 | 0,14 | 0,08 |
Для построения гистограммы относительных частот на оси абсцисс откладываются частичные интервалы длины
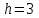 , а над ними проводятся горизонтальные отрезки на расстоянии
, а над ними проводятся горизонтальные отрезки на расстоянии 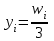 (рис. 1).
(рис. 1).
б) Перейдем к вариантам, положив их равными серединам частичных интервалов
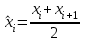 , где
, где 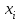 ,
, 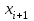 – концы интервалов. Тогда табл. 2 превратится в табл. 3:
– концы интервалов. Тогда табл. 2 превратится в табл. 3:Таблица 3
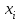 | 13,5 | 16,5 | 19,5 | 22,5 | 25,5 | 28,5 |
 | 0,04 | 0,12 | 0,24 | 0,38 | 0,14 | 0,08 |
Отметим на плоскости точки
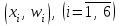 и, соединив соседние точки, получим полигон относительных частот (рис. 2).
и, соединив соседние точки, получим полигон относительных частот (рис. 2).
в) Эмпирическая функция распределения
 строится по закону:
строится по закону: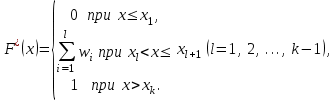
В нашем случае получаем:
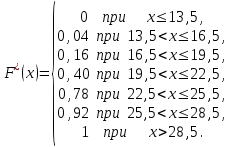
График функции
 представлен на рис. 3.
представлен на рис. 3.
Пример 2.В условиях примера 1 найти статистические оценки.
Решение Обратимся к табл. 3:
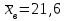 ;
; 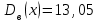 ;
;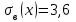 .
.Контрольные вопросы:
-
Что такое выборка? -
Что такое варианта выборки и частота? -
Как графически изображается выборка? -
Точечные оценки выборки.
Задачи на закрепление материала
Статистический ряд задан таблицей. Требуется:
а) построить гистограмму относительных частот;
б) перейти к вариантам и построить полигон относительных частот;
в) записать эмпирическую функцию распределения и построить ее график;
г) найти точечные оценки
 ,
, 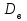 ,
, 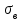 ;
;| 1. |
| ||||||||||||
| 2. |
| ||||||||||||
| 3. |
| ||||||||||||
| 4. |
|
Тема лекции: Интервальные оценки параметров распределения
План:
-
Интервальная оценка математического ожидания нормального распределения. -
Интервальная оценка среднего квадратического отклонения нормального распределения. -
Интервальная оценка вероятности события
Определение: Интервальнойназывают оценку, которая определяется двумя числами – концами интервала.
Так как любая оценка
 есть некоторое приближение оцениваемой величины a, то возникает вопрос об оценке точности данного приближения, т. е. можно ли утверждать, что
есть некоторое приближение оцениваемой величины a, то возникает вопрос об оценке точности данного приближения, т. е. можно ли утверждать, что 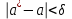 для некоторого
для некоторого 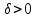 .
.Однако статистические методы не позволяют категорически утверждать, что оценка
 удовлетворяет неравенству
удовлетворяет неравенству 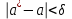 . Можно лишь говорить о вероятности наступления события, заключающегося в том, что мы получили оценку с точностью :
. Можно лишь говорить о вероятности наступления события, заключающегося в том, что мы получили оценку с точностью : 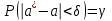 . Эта вероятность называется доверительной вероятностью (или надежностью), а интервал
. Эта вероятность называется доверительной вероятностью (или надежностью), а интервал 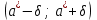 – доверительным интервалом. Вероятность того, что интервал
– доверительным интервалом. Вероятность того, что интервал 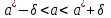 заключает в себе неизвестный параметр a, равна . Обычно надежность выбирают близкой к единице (0,95; 0,99; 0,999).
заключает в себе неизвестный параметр a, равна . Обычно надежность выбирают близкой к единице (0,95; 0,99; 0,999).-
Интервальная оценка математического ожидания нормального распределения
Если случайная величина распределена нормально и среднее квадратическое отклонение известно, то доверительный интервал для оценки математического ожидания a
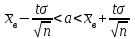 , (1)
, (1)где n – объем выборки, t находится из равенства
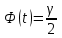 по таблице значений функции Лапласа
по таблице значений функции Лапласа 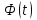 .
.Если неизвестно, то в формуле (1) оно заменяется на исправленное среднее квадратическое отклонение S, t заменяется на
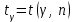 , которое находится по таблице (приложение )
, которое находится по таблице (приложение )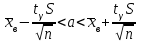 . (2)
. (2)-
Интервальная оценка среднего квадратического отклонения нормального распределения
Доверительный интервал для оценки среднего квадратического отклонения
нормального распределения с заданной надежностью находится по формуле
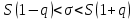 , (3)
, (3)где
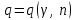 находится по таблице (приложение ).
находится по таблице (приложение ).Пример 1. Дано распределение частот выборки (табл. 1). Найти доверительные интервалы для математического ожидания a и среднего квадратического отклонения с доверительной вероятностью = 0,95, если известно, что генеральная совокупность распределена по нормальному закону
Таблица 1
 | 12 –15 | 15 – 18 | 18 – 21 | 21 – 24 | 24 – 27 | 27 – 30 |
 | 2 | 6 | 12 | 19 | 7 | 4 |
Решение
Имеем:
 ,
, 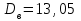 ,
, 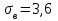 . Так как объем выборки
. Так как объем выборки 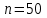 , то находим
, то находим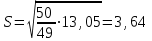 .
.По таблице приложения находим
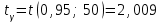 .
.Подставляя полученные значения S и t в формулу (2), получим
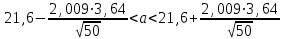
или
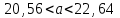 .
.По таблице приложения найдем
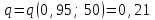 .
.Подставляя значения S и q в формулу (3), получим
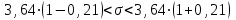
или
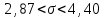 .
.3.Интервальная оценка вероятности события
Интервальной оценкой (с надежностью
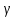 ) неизвестной вероятности р биномиального распределения по относительной частоте
) неизвестной вероятности р биномиального распределения по относительной частоте