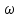служит доверительный интервал (с приближенными концами р₁ и р₂) ,

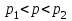где

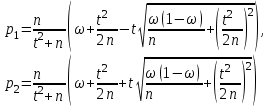
n- общее число испытаний;

m- число появления события;

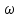- относительная частота, равная отношению m/n;

t- значение аргумента функции Лапласа, при котором . ( - заданная надежность).
Замечание: При больших значениях n (порядка сотен) можно принять в качестве приближенных границ доверительного интервала


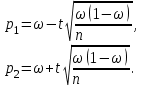
Пример: Производятся независимые испытания с одинаковой, но неизвестной вероятностью р появления события А в каждом испытании. Найти доверительный интервал для оценки вероятности р с надежностью 0,95, если в 60 испытаниях событие А появилось 15 раз.
Решение: По условию, n=60, m=15, =0.95. Найдем относительную частоту появления события А: .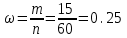

Найдем t из соотношения 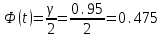. По таблице функции Лапласа находим t=1,96.

Найдем границы искомого доверительного интервала:



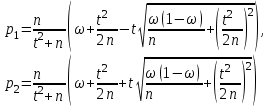
Подставив в эти формулы n=60, 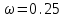, t=1,96, получим р₁=0,16, р₂=0,37.

Итак, искомый доверительный интервал .
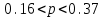Пример: Изготовлен экспериментальный игровой автомат, который должен обеспечить появление выигрыша в одном случае из 100 бросаний монеты в автомат. Для проверки пригодности автомата произведено 400 испытаний, причем выигрыш появился 5 раз. Найти доверительный интервал, покрывающий неизвестную вероятность появления выигрыша с надежностью =0.999.
Решение: Найдем относительную частоту появления выигрыша

---

.

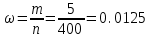
Найдем t из соотношения 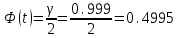. По таблице функции Лапласа находим t=3,3.

Учитывая, что n=400 велико, используем для отыскания границ доверительного интервала приближенные формулы:

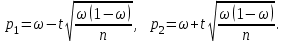
Подставив в эти формулы n=400, 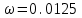, t=3,3,

получим р₁= -0,0058, р₂= 0,0308.

Итак, искомый доверительный интервал .

---

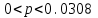Смотрите также файлы

• Справка о наличии основных средств по состоянию на 13. 03. 2023 год Государственное бюджетное учреждение здравоохранения Московской области.docx

• Общие условия договора потребительского займа с лимитом кредитования.pdf

• Отчет по учебной практике уп. 04 Выполнение работ по профессии рабочего.docx

• Арман Марлен тмо 212 Психология сро10 Восприятие окружающих в процессе общения.docx

• Программа среднего профессионального образования 44. 02. 02 Преподавание в начальных классах Дисциплина Теоретические и прикладные аспекты методической работы учителя начальных классов Практическое занятие 2.pdf