Файл: Фгбоу впо угту.docx

(см.пункт 3.1.3).

3.3.3 Напряжения изгиба зубьев косозубых цилиндрических колёс при проверочном расчёте на выносливость вычисляются по формуле /2, с.46/

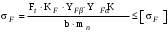, (3.13)

где 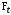– окружная сила, Н; 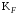– коэффициент нагрузки; 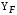– коэффициент формы зуба; 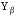– коэффициент, компенсирующий погрешности, возникающие из–за применения для косых зубьев той же расчётной схемы, что и для прямых;

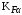– коэффициент, учитывающий неравномерность распределения нагрузки между зубьями;

b – ширина колеса, находящаяся в зацеплении (минимальная), мм;

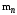– модуль нормальный, мм.

В зацеплении колес косозубой передачи действуют следующие силы /2, с.158/:

– окружная ;

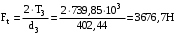– радиальная ;

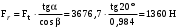– осевая .

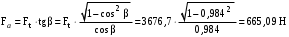(Здесь α – угол зацепления в нормальном сечении  (ГОСТ 13755-81)) .

Коэффициент нагрузки /2, с.42/:

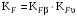, (3.14)

где 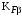– коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба (по ширине венца); 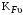– коэффициент, учитывающий дополнительные динамические нагрузки (динамический коэффициент). Принимаем 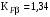/2, с.43/ с учётом, что твёрдость колёс менее НВ 350, коэффициент 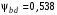, а каждое из колёс расположено несимметрично относительно опор. Назначим 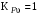, учитывая дополнительно, что окружная скорость υ = 1,64 м/с < 3 м/с, а степень точности принята восьмая.

Тогда, по формуле (3.14)

.

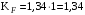Без расчётов, руководствуясь только рекомендацией /2, с.47/, возьмём .

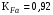Коэффициент

---

определим по формуле /2, с.46/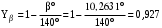



(Здесь β° – вычисленный ранее угол наклона зубьев).

Коэффициент формы зуба для косозубых колёс зависит от эквивалентного числа зубьев /2, с.46/, которое составляет:

для шестерни ,

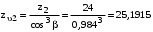для колеса .

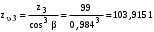Для эквивалентных чисел зубьев соответственно шестерни и колеса находим /2, с.42/

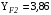и .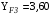

Подстановка подготовленных численных значений в формулу (3.13) даёт для шестерни и колеса соответственно:

;

.

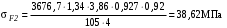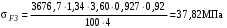Это значительно меньше вычисленных в пункте 3.1.4 допускаемых напряжени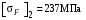й и .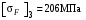

Результат расчёта свидетельствует о большой недогрузке зубьев по напряженности изгиба. Это характерно для колес с малой твердостью и не являются отрицательным результатом проверочного расчёта. Ведь все геометрические параметры колёс определены проектным расчётом по контактным напряжениям.

3.3.4 Напряжения изгиба при кратковременных перегрузках вычисляются также по формуле (3.13), куда вместо окружной силы F_t, рассчитанной для длительно передаваемой мощности, следует подставить окружную силу при кратковременных перегрузках

.

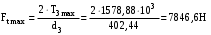После подстановки в формулу (3.13) получаем при перегрузках соответственно для шестерни и колеса напряжения изгиба

;

.

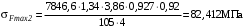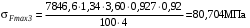Эти напряжения значительно меньше вычисленных в пункте 3.1 допускаемых напряжени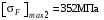й и .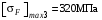

3.3.5 Геометрические параметры колёс косозубой передачи, обоснованные в результате расчётов, сведены в таблицу 3.1.
Таблица 3.1 – Геометрические параметры колес зубчатой передачи

---

Параметры	Шестерня	Колесо
Межосевое расстояние	250
Нормальный модуль, мм	4
Угол наклона зубьев, град	10°15'47"
Число зубьев	24	99
Направление зубьев	левое и правое	правое и левое
Делительные диаметры, мм	97,56	402,44
Диаметры вершин зубьев, мм	105,56	410,44
Диаметры впадин зубьев, мм	87,56	392,44
Ширина венцов колёс, мм	105	100

Литература.

Чернавский С.А

Устюгов И.И. 1981

Жингаровский А.Н.

---