Добавлен: 11.01.2024
Просмотров: 36
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Выполнил: Сухоруков Е.В.
группа: ЭОТб(до)зу-15-4
Вариант 6
Основные газодинамические понятия и зависимости
Задача 4. Звук работы двигателя зарегистрирован через t = 2,5с после пролета самолета над пунктом регистрации. Определить скорость пролета, если высота H = 3 км.
Решение:
Самолет летит горизонтально на высоте H = 3 км со сверхзвуковой скоростью. Звук двигателя зарегистрирован через t = 2,5с после пролета самолета над пунктом регистрации. Скорость звука v0=330 м/с.
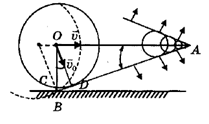
В - точка, в которой находится пункт регистрации, А - точка, в которой находится самолет в момент времени t. Из каждой точки, которую пролетает самолет, распространяется сферическая звуковая волна. Если сложить все звуковые волны для момента, когда самолет находится в точке А, то получится волновая поверхность в виде конуса. По мере движения самолета эта поверхность (фронт волны) распространяется со скоростью звука v0. Это есть ударная звуковая волна.
На рис. OD⊥AB, причем
, 
, 
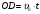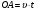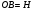и 
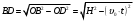.∠BOD=∠BAO (как углы с взаимно перпендикулярными сторонами).
Поэтому прямоугольные треугольники BOD и BOA подобны.
Из подобия следует, что
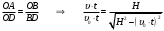
Выразим отсюда скорость пролета самолета над пунктом регистрации:
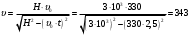м/с.Ответ: скорость пролета 343 м/с.
Определение расхода газа через сопло
Задача 1. Воздух истекает из баллона в атмосферу через конфузорное сопло с диаметром выходного сечения d = 0,03 м. Давление газа в баллоне р0 = 15 атм = 1,5 МПа и температура – T0 = 500 К. Найти массовый секундный расход воздуха через сопло.
Решение:
Отношение давлений составляет
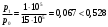
При истечении газа из комбинированного сопла Лаваля в окружающую среду с давлением меньше критического в самом узком сечении сопла устанавливается критическое давление и критическая скорость.
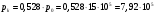ПаТемпература в критическом сечении сопла при адиабатном истечении
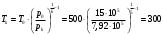КТемпература на выходе сопла при адиабатном истечении
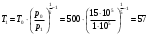КПоэтому скорость истечения будет равна критической и определяется по формуле
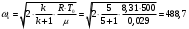м/сМаксимальный секундный расход воздуха
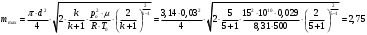кг/с.Ответ: 2,75 кг/с.
Течение газа при наличии энергообмена
Задача 2. Поток воздуха нагревается в цилиндрической трубе за счет теплоты сгорания топлива, расход которого составляет 5% от расхода воздуха. До подогрева скорость воздуха V1 = 50 м/с, давление р1 = 1,0 МПа, температура торможения T01 = 550 К. Найти скорость и давление газа в сечении трубы, где температура тор- можения T02 = 1500 К.
Принять k = 1,33; R = 291 Дж/(кг К). Трением пренебречь.
Решение:
Воспользуемся теоремой импульсов переписанной (для труб с прямолинейной осью) в скалярной форме:
(1)Применим ее в виде теоремы сохранения импульсов, т.е. при
=0.Откуда:
(2) Здесь,
(3)
-газодинамическая функция, 
(4)-коэффициент скорости,1 - коэффициент скорости на входе,
2- коэффициент скорости на выходе из трубы.
(5)
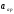-критическая скорость звука, Gt-секундный расход газа.
Найдем
и 
.Так как для воздуха к=1,4 
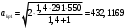м/сек.Внутри трубы к=1,33
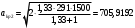м/сек.
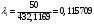. Так как расход Gt2 больше Gt1 на 5% то 
. 
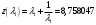. Подставим найденные значения в формулу (2)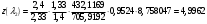
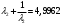
Решив уравнение найдем два значения 2.
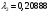
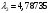
Реальным будет только первое решение, поскольку подогревом нельзя перевести дозвуковой поток в сверхзвуковой. Зная коэффициент скорости мы можем найти скорость , этому коэффициенту соответствующую:
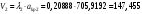м/сек.
(6)где по уравнению расхода
(7)-коэффициент восстановления полного давления. -газодинамическая функция. B1G и B2G здесь постоянные .
(8)Вычисляем B1G и B2G по формуле (8):
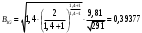
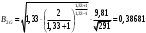. Найдем значения qk=1.4(1) , qk=1,33(2) , л=1,4(1), и л=1,33(2) по таблицам газодинамических функций:
qk=1.4(1)=0,18816 , qk=1,33(2)=0,32362,
л=1,4(1)=0,99163, л=1,33(2) =0,97408.
Подставим все найденные значения в формулы (6),(7) и (8).
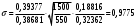
Найдем из формулы (6) р2:
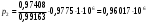
р2=9,6017 ата.
Ответ: V2=147,455 м/сек, р2=9,6017 ата.