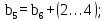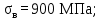
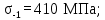
- для колеса

По таблице 3.2 [4] выбираем предельные значения размеров заготовки шестерни (D_пред - диаметр) и колеса (S_пред - толщина обода или диска):

- для шестерни D_пред = 200 мм,

- для колеса S_пред = 125 мм.

Определяем допускаемые контактные напряжения .

Определяем коэффициент долговечности для зубьев шестерни K_HL5 и колеса K_HL6


где N_HO5=10·10⁶ циклов – число циклов перемены напряжений, соответствующее пределу выносливости [4];

N₅ – число циклов перемены напряжений за весь срок службы
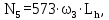(4.2)
где ω₃ - угловая скорость быстроходного вала,

L_h=42000 ч. – срок службы привода;



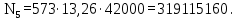
Т.к. 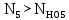, то принимаем K_HL5 = 1.


где N_HO6=10·10⁶ циклов – число циклов перемены напряжений, соответствующее пределу выносливости [4];

N₆ – число циклов перемены напряжений за весь срок службы,
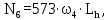(4.4)
где ω₄- угловая скорость тихоходного вала,

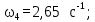
L_h=42000 ч. – срок службы привода;



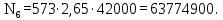
Т.к. 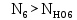, то принимаем K_HL6 = 1.

Определяем допускаемое контактное напряжение, соответствующее пределу выносливости при числе циклов перемены напряжений N_HO5 и N_HO6
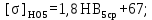(4.5)

---

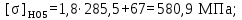
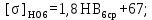(4.6)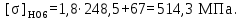


Определяем допускаемые контактные напряжения для зубьев шестерни и колеса
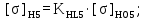(4.7)

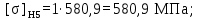
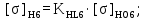(4.8)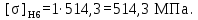


Расчет будем вести по наименьшему значению 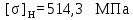.125>

---

4.2 Расчет допускаемых напряжений изгиба
Определяем коэффициент долговечности для зубьев шестерни K_FL5 и колеса K_FL6





где циклов – число циклов перемены напряжений, соответствующее пределу выносливости [4];

N₅ – число циклов перемены напряжений за весь срок службы.

Т.к. N₅>N_FO и N₆>N_FO, то принимаем K_FL5=K_FL6 = 1.

Определяем допускаемое напряжение изгиба соответствующее пределу изгибной выносливости при числе циклов перемены напряжений
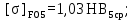(4.11)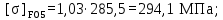

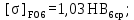(4.12)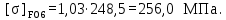


Определяем допускаемые напряжения изгиба для зубьев шестерни и колеса
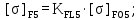(4.13)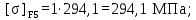


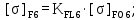(4.14)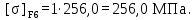


Расчет будем вести по наименьшему значению из полученных, то есть
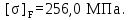
4.3 Проектный расчет закрытой цилиндрической зубчатой передачи
Определяем межосевое расстояние


где - вспомогательный коэффициент для прямозубой передачи [4];

u – передаточное число редуктора;

T₄ – вращающий момент на тихоходном валу, Н·м;

---

- коэффициент ширины венца колеса, равный 0,28…0,36 [4], =0,4;

- допускаемое контактное напряжение колеса, ;

- коэффициент, учитывающий распределению нагрузки по ширине венца; .



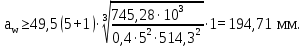
Полученное значение внешнего делительного диаметра округляем до ближайшего по стандартному ряду до = 200 мм.

Определяем модуль зацепления


где - вспомогательный коэффициент для прямозубой передачи [4];

d₆ – делительный диаметр колеса.




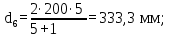
b₆ – ширина венца колеса;
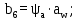(4.18)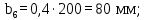


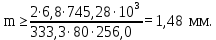
– допускаемое напряжение изгиба;



Полученное значение модуля округляем до стандартного, получаем m =2,00 мм.

Определяем суммарное число зубьев шестерни и колеса


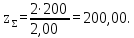Полученное значение округляем до целого числа и берём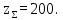

Определяем число зубьев шестерни

---

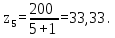
Округляем полученное значение до целого, получаем .

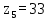Определяем число зубьев колеса
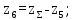(4.21)
.

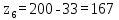Определяем фактическое передаточное число u_ф и проверяем его отклонение от заданного



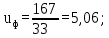
(4.23)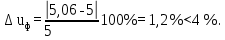


Определяем фактическое межосевое расстояние




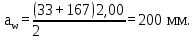
Определяем фактические основные геометрические параметры передачи для шестерни и колеса:

- делительный диаметр шестерни и колеса
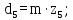(4.25)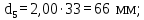

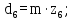(4.26)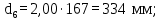


- диаметр вершин зубьев шестерни и колеса
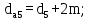(4.27)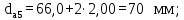

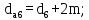(4.28)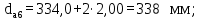


- диаметр впадин зубьев шестерни и колеса
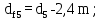(4.29)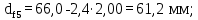

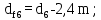(4.30)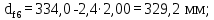


- ширина венца шестерни и колеса
(4.31)

---

Смотрите также файлы

• I тур.pptx

• Практическая работа 2 Практическая работа 2 Характеристика детского коллектива (9 класс).docx

• Пензенской области присущи следующие экологические проблемы Экологические.pptx

• Сумин Александр Сергеевич, магистрант, фгбоу во Приамурский государственный университет имени ШоломАлейхема.docx

• Правовые аспекты использования программного обеспечения лицензии.docx