Добавлен: 11.01.2024
Просмотров: 22
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Санкт-Петербургский государственный университет телекоммуникаций
им. проф. М.А. Бонч-Бруевича
факультет Информационных систем и технологий
Отчёт по лабораторной работе №4
Тема: «Исследование устойчивости линейной САУ»
Предмет: Основы теории управления
Выполнил: студент группы
.
Санкт-Петербург
2012
Цель работы
-
Познакомиться с основными методами определения устойчивости линейной системы -
Научиться применять различные критерии устойчивости САУ
Задачи работы
-
Получить представление о критериях устойчивости -
Исследовать систему на устойчивость с помощью различных критериев
Ход работы
Вариант 1
Дана структурная схема системы:

Рисунок 1 – Структурная схема САУ
В качестве передаточной функции W(p) задано следующее выражение:
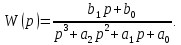
В качестве передаточной функции обратной связи задано выражение:
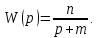
Коэффициенты имеют следующие значения:
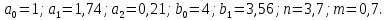
Исследовать систему на устойчивость с помощью различных критериев.
1. Исследование устойчивости системы с использованием критерия Гурвица.
Для данной САУ, которая является САУ с обратной отрицательной связью, необходимо найти передаточную функцию разомкнутой системы, которая находится из выражения:
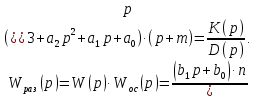
Для того чтобы исследовать систему на устойчивость по критерию Гурвица необходимо получить передаточную функцию замкнутой системы, которая находится из выражения:
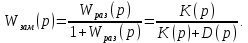
Для нахождения характеристического уравнения САУ приравниваем к нулю знаменатель
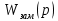
:
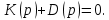
Обозначая знаменатель передаточной функции как С(р) характеристическое уравнение принимает вид:
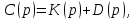
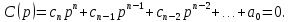
Проведя математические преобразования, получена передаточная функция замкнутой системы:
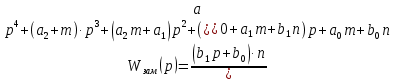
Полученное выражение передаточной функции замкнутой системы позволяет провести расчёт коэффициентов полинома:
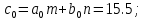
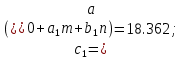
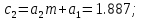
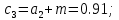
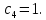
Главный определитель Гурвица для САУ имеет следующий вид:
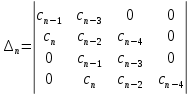
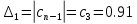
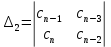 =
=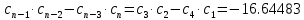 <0
<0При расчёте получилось, что главный диагональный минор определителя Гурвица меньше нуля. А это значит, что САУ неустойчивая.
2. Исследование устойчивости системы с использованием критерия Рауса.
Используя все коэффициенты с первого пункта, составим таблицу Рауса.
Таблица 1 – Таблица Рауса
| r | Строки | Столбцы | ||
| 1 | 2 | 3 | ||
| - | 1 | 1 | 1,887 | 15,5 |
| - | 2 | 0,91 | 18,362 | 0 |
| 1,098 | 3 | 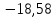 | 15,5 | 0 |
| | 4 | | 0 | 0 |
| | 5 | 0 | 0 | 0 |
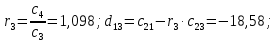
Так как коэффициент первого столбца меньше нуля, то система не устойчивая и дальнейший расчёт не имеет смысла.
Для исследования САУ по приведённым выше критериям в среде Matlabнеобходимо воспользоваться функцией, текст которой приведён ниже:
function [Ust, Mnrs, Mtrx] = raus_gur(D)
ifisa(D, 'lti')
[B, D] = tfdata(D, 'v');
end
Ust = 1;
if length(D(:)) < 4
Mtrx = NaN; Mnrs = NaN;
if any(D(:) <= 0)
Ust = 0;
end
return
end
D = D(:);
n = length(D) - 1; % Размеры матрицы Гурвица
A = [zeros(n-1, 1); D(end:-1:1); zeros(n-2, 1)];
Mtrx = zeros(n, n); % Заготовка матрицы Гурвица
Mnrs = zeros(n-2, 1); % Векторминоров
fori = 1:n
Mtrx(:, i) = A((n - i)*2 + 1:3*n - 2*i);
end
fori = 2:n-1
Mnrs(i-1) = det(Mtrx(1:i,1:i));
end
if any([D(:); Mnrs(:)] <= 0)
Ust = 0;
end
Для вызова этой функции необходимо в командной строке прописать :
>> [A, B] = raus_gur([1 0.91 1.887 18.362 15.5])
После чего программа начнёт работу и выдаст следующие результаты работы:
A = 0
B = -16.6448
-318.4679
>>
Приведённые результаты свидетельствуют о том, что система не устойчива.
3. Исследование устойчивости системы с использованием критерия Михайлова.
Исходя из начальных условий, построим годограф Михайлова в среде Matlab. Текст программы для построения годографа:
a0=15,5;
a1 = 18,362;
a2 =1,887;
a3=0,91;
a4=1;
Re=[];Im=[];
for w=0.01:1:45,
Njw=a4*((w*j)^4)+ a3*((w*j)^3)+a2*((w*j)^2)+a1*(w*j)+(a0);
Re = real(Njw);
Im = imag(Njw);
plot(Re, Im, 'k.')
xlabel('Re(W)')
ylabel('Im(W)')
hold on
end
hold off
grid on
Результат работы:
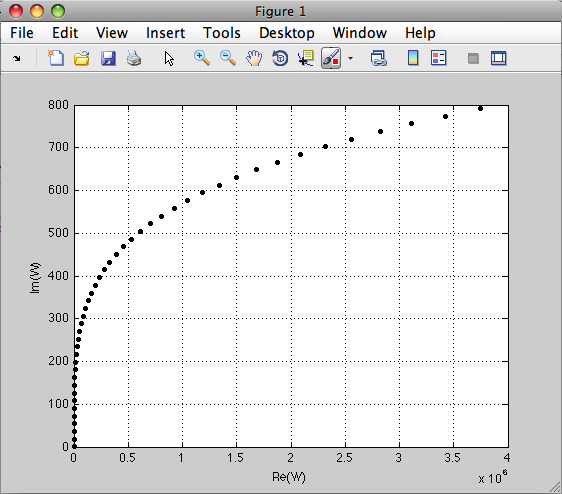
Рисунок 2 – Годограф Михайлова в среде Matlab
С рисунка видно, что годограф не обходит nквадрантов в положительном направлении, из чего следует вывод, что САУ не устойчивая.
4. Исследование устойчивости системы с использованием критерия Найквиста.
Исходя из начальных условий, построим годограф Найквиста в среде Matlab.Текст программы для построения годографа:
t=tf([3.56 4], [1 0.21 1.74 1]);
nyquist(t)
Рисунок 3 – Годограф Найквиста в среде Matlab
С рисунка видно, что годограф охватывает начало координат, что свидетельствует о том, что система не устойчива.
Вывод
При исследовании САУ на устойчивость использовались четыре критерия, которые показали, что с данными варианта 1 система не устойчива.