ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 113
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
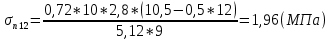
Максимальные напряжения в коренных листах, МПа:
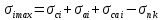 (2.17)
(2.17)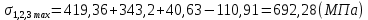
Максимальные напряжения в коренных листах, МПа:
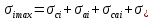 (2.18)
(2.18)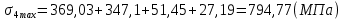
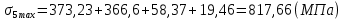
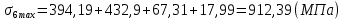
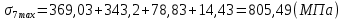
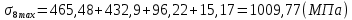
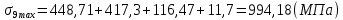
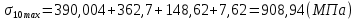
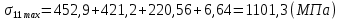
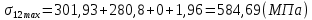
Результаты расчёта максимальных напряжений сводятся в таблицу 3.
Таблица 3. Максимальные напряжения в лисах рессоры.
| Напряжение в листах, МПа | Номер листа | |||||||||
| 1, 2, 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| σci | 419,36 | 369,03 | 373,23 | 394,19 | 369,03 | 465,48 | 448,71 | 390,004 | 452,9 | 301,93 |
| σai | 343,2 | 347,1 | 366,6 | 432,9 | 343,2 | 432,9 | 417,3 | 362,7 | 421,2 | 280,8 |
| σcai | 40,63 | 51,45 | 58,37 | 67,31 | 78,83 | 96,22 | 116,47 | 148,62 | 220,56 | 0 |
| σni | 110,91 | 27,19 | 19,46 | 17,99 | 14,43 | 15,17 | 11,7 | 7,62 | 6,64 | 1,96 |
| σi max | 692,28 | 794,77 | 817,66 | 912,39 | 805,49 | 1009,77 | 994,18 | 908,94 | 1101,3 | 584,69 |
По таблице необходимо определить наличие листов, напряжение в которых превышает допускаемую величину максимальных рабочих напряжений [σ]Р = 840 МПа. Если таких листов нет, указать это. При наличии таких листов указать их номера и возможные конструктивные изменения с целью уменьшения максимальных напряжений.
Для уменьшения величины максимальных напряжений необходимо увеличить количество рессор на один лист и повторить расчёты с формулы (1.8).
Также возможно и другое конструктивное решение – выполнить скосы на концах листов ступенчатой части. В этом случае
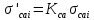 .
.Принимаем
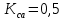 и выполняем расчёт максимальных напряжений для листов.
и выполняем расчёт максимальных напряжений для листов.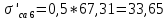
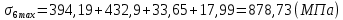
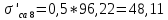
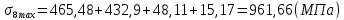
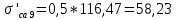
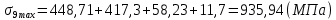
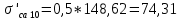
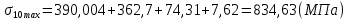
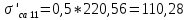
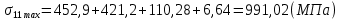
По окончании расчётов необходимо на миллиметровой бумаге начертить рассчитанную листовую рессору с указанием основных линейных параметров.
Масштаб длин листов рессоры взять 1:4 или 1:5. Масштаб для толщины листа взять 1:1 или 1:2. На этом же листе сделать таблицу со следующими параметрами по отдельным листам рессоры:
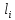 , см;
, см; 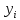 , см;
, см; 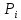 , кН;
, кН; 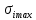 , МПа.
, МПа.Количество листов:
 (1.8)
(1.8)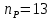 (листов)
(листов)Количество листов принимается с округлением в меньшую сторону и дополнительным вычитанием одного листа.
Общее количество листов разбивается на количество коренных листов m и количество ступенчатых рессор n. При определении количества коренных листов необходимо придерживаться следующего правила: если общее количество листов рессор меньше восьми включительно, брать два коренных листа; в других случаях – три.
m = 3, n = 10
Шаг удлинения листов, см:
 (1.9)
(1.9)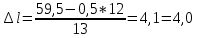 (см)
(см)Полученный шаг удлинения листов округляется с шагом 0,5 см. Например, если получилось 4,9 см, то округлить до 5,0 см, если получилось 5,7 см, то округлить до 5,5 см.
Длина первого ступенчатого листа (самого длинного), см:
 (1.10)
(1.10)где i = m+1 – номер первого ступенчатого листа.
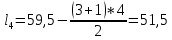 (см)
(см)Полученную длину первого ступенчатого листа округляем в меньшую сторону до целого значения.
Длины остальных листов ступенчатой части, см:
 (1.11)
(1.11)где i – шаг расчёта ступенчатого листа, i = n–m–1…1 (с шагом минус 1).
 0,5 * 12 + 9 *
0,5 * 12 + 9 * 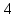 = 42 (см)
= 42 (см) 0,5 * 12 +8 *
0,5 * 12 +8 * 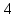 = 38 (см)
= 38 (см) 0,5 * 12 + 7 *
0,5 * 12 + 7 * 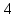 = 34 (см)
= 34 (см) 0,5 * 12 + 6 *
0,5 * 12 + 6 * 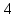 = 30 (см)
= 30 (см) 0,5 * 12 + 5*
0,5 * 12 + 5* 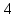 = 26 (см)
= 26 (см) 0,5 * 12 + 4 *
0,5 * 12 + 4 * 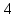 = 22(см)
= 22(см) 0,5 * 12 + 3 *
0,5 * 12 + 3 * 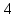 = 18 (см)
= 18 (см) 0,5 * 12 + 2*
0,5 * 12 + 2* 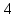 = 14 (см)
= 14 (см) 0,5 * 12 + 1 *
0,5 * 12 + 1 * 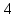 = 10 (см)
= 10 (см)Момент инерции сечения листа, см4:
 (1.12)
(1.12) = 4,1 (см4)
= 4,1 (см4)Действительный статический прогиб без учета сил трения, см:
 , (1.12)
, (1.12)где ln – натуральный логарифм.
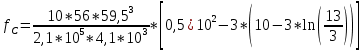 = 4,54 (см)
= 4,54 (см)Коэффициент динамичности прогибов:
 (1.13)
(1.13)Результаты расчёта величин КДП для различных значений μ и РТ/Ра сводим в таблицу 1.
Коэффициент динамичности прогибов для μ=0,4, PТ
/Pa = 1:
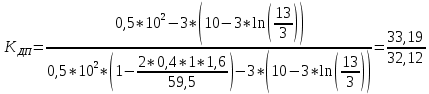 = 1,03
= 1,03Коэффициент динамичности прогибов для μ=0,4, PТ/Pa=fc/ya=4,54/3,4=1,33=1:
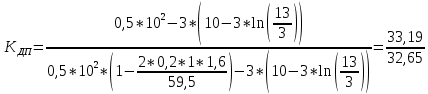 = 1,01
= 1,01Коэффициент динамичности напряжений:
 (1.14)
(1.14)Результаты расчёта величин КДН для различных значений μ, РТ/Ра и РС/Ра сводим в таблицу 1.
Коэффициент динамичности напряжений при μ = 0,4 и Pc/Pa = 1:
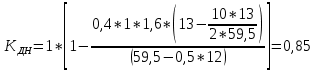
Коэффициент динамичности напряжений при μ = 0,2 PТ/Pa=fc/ya=4,54/3,4=1,33=1:
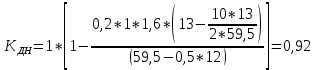
Таблица 1. Коэффициенты динамичности.
Результаты расчёта величин
 для различных значений
для различных значений  ,
,  и
и  сводим в таблицу 1.
сводим в таблицу 1.Таблица 1. Коэффициенты динамичности
| Коэффициенты динамичности | µ | Отношение  , ,  | |||||
| 9 | 8 | 6 | 4 | 2 | 1 | ||
 | 0,1 | 1,08 | 1,07 | 1,05 | 1,03 | 1,01 | 1,008 |
| 0,2 | 1,17 | 1,15 | 1,11 | 1,07 | 1,03 | 1,01 | |
| 0,3 | 1,29 | 1,25 | 1,17 | 1,11 | 1,05 | 1,02 | |
| 0,4 | 1,43 | 1,36 | 1,25 | 1,15 | 1,07 | 1,03 | |
| 0,5 | 1,6 | 1,5 | 1,33 | 1,19 | 1,09 | 1,04 | |
| 0,6 | 1,82 | 1,67 | 1,43 | 1,23 | 1,11 | 1,05 | |
| 0,7 | 2,11 | 1,88 | 1,54 | 1,27 | 1,13 | 1,06 | |
| 0,8 | 2,52 | 2,15 | 1,67 | 1,31 | 1,15 | 1,07 | |
 | 0,1 | 0,07 | 0,09 | 0,13 | 0,21 | 0,46 | 0,96 |
| 0,2 | 0,04 | 0,05 | 0,1 | 0,18 | 0,43 | 0,92 | |
| 0,3 | 0,01 | 0,25 | 0,06 | 0,15 | 0,4 | 0,9 | |
| 0,4 | -0,02 | -0,007 | 0,03 | 0,11 | 0,36 | 0,85 | |
| 0,5 | -0,05 | -0,04 | 0,00 | 0,08 | 0,33 | 0,83 | |
| 0,6 | -0,08 | -0,07 | -0,03 | 0,05 | 0,3 | 0,8 | |
| 0,7 | -0,12 | -0,1 | -0,06 | 0,01 | 0,26 | 0,76 | |
| 0,8 | -0,15 | -0,14 | -0,09 | -0,01 | 0,23 | 0,73 | |