Файл: Введение 1 Изучение колебательных явлений в курсе физики средней школы как методическая проблема.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 11.01.2024

Просмотров: 89

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Введение 1 Изучение колебательных явлений в курсе физики средней школы как методическая проблема 1.1 Научно-методический анализ содержания раздела «Механические колебания» 1.1.1 Свободные колебания в системах без трения: математический и пружинный маятники Изучение колебаний начинают с введения понятия о колебательном движении, которое является одним из основных в этой теме. Учащиеся уже знакомы с периодическими, т. е. повторяющимися через равные промежутки времени, движениями (например, с равномерным движением по окружности). Разновидность периодического движения – колебательное, т. е. такое движение, при котором тело перемещается от своего положения равновесия то в одну сторону, то в другую. Приводят примеры колебательных движений и демонстрируют системы тел, в которых при определенных условиях могут существовать колебания (вертикальный и горизонтальный пружинные маятники, груз на нити, ножовочное полотно, зажатое в тисках, и др.).На примере этих колебательных систем подчеркивают то общее, что характерно для любых из них: наличие устойчивого положения равновесия фактор инертности, обеспечивающий прохождение телом положения равновесия и, таким образом, установление колебательного движения вместо простого возвращения тела в положение равновесия, и, наконец, достаточно малое трение в системе. Рисунок 1 – Различные системы.Учащиеся убеждаются в наличии этих признаков у каждой из демонстрируемых колебательных систем. После этого им можно предложить ответить па вопрос, могут ли возникнуть колебания в системах, представленных на рисунке 1, и проверить свой ответ экспериментально.Вводят понятие о свободных колебаниях. Колебания, возникающие в системе, выведенной из положения равновесия и представленной самой себе, называют свободными. Если в системе отсутствует трение, то свободные колебания называют собственными, они происходят с собственной частотой, которая определяется только параметрами системы. Колебательная система, лишенная трения, ­ идеализация, но при малом коэффициенте затухания различие между свободными и собственными колебаниями слишком незначительно, чтобы его учитывать (при добротности системы в несколько единиц оно не превышает нескольких процентов). Поэтому в школьном преподавании физики понятия свободных и собственных колебаний не разграничивают и учащиеся знакомятся только с понятием свободных колебаний.Одно из важнейших понятий теории колебаний – гармоническое колебание. Это понятие широко используют по двум причинам: любое периодическое негармоническое движение может быть представлено в виде суммы ряда гармонических колебаний кратных частот, причем эти последние можно выделить и наблюдать. Кроме того, существует много таких колебательных систем, колебания которых с большой точностью можно считать гармоническими.Программа общеобразовательной средней школы обычно предполагала впервые ознакомить школьников с понятием гармонического колебания в последнем классе средней школы при изучении электромагнитных колебаний. Но существует реальная возможность сделать это уже при изучении механических колебаний.При этом возможен следующий подход: используя связь равномерного движения по окружности и колебательного движения, получают закон изменения координаты гармонически колеблющегося тела со временем .Для этого вначале на опыте показывают, что тень от шарика, равномерно движущегося по окружности, совершает колебательное движение (рисунок 2). Рисунок 2 ­ Установка для эксперимента с пружинным маятником и шариком.На установке возбуждают колебания пружинного маятника. Убеждаются в том, что маятник совершает такие же колебания, что и тень на экране от шарика, при этом частоту вращения шарика подбирают таким образом, чтобы колебания были синхронными.Затем учащиеся самостоятельно выполняют задание: найти выражение для координаты проекции на ось X материальной точки А. движущейся равномерно со скоростью по окружности (рис. 3). Рисунок 3 ­ Равномерное движение материальной точки A со скоростью по окружностиПолучают выражение . Сообщают, что движение, в котором координата тела меняется по такому закону, называют гармоническим колебанием. Так как маятник и тень шарика на экране совершают одинаковое движение (колеблются синхронно), делаем вывод: колебания маятника могут быть описаны тем же уравнением, т.е. при определенных условиях они тоже являются гармоническими. В завершающем обучение классе при изучении электромагнитных колебаний это определение можно расширить, показав, что любая величина, изменяющаяся по такому закону, совершает гармоническое колебание (например, заряд конденсатора в контуре, сила тока и напряжение в контуре и др.).Возможен и другой подход к введению понятия о гармоническом колебании: рассматривают динамику свободных колебаний пружинного (рис. 4, а) и математического (рис. 4, б) маятников под действием соответственно силы упругости и силы тяжести в отсутствие силы трения. Для каждого из этих случаев на чертеже изображают силы, действующие на маятник, и записывают уравнение движения в проекциях на ось OX маятника, выведенного из положения равновесия и предоставленного самому себе, из которого получают (для пружинного маятника) и (для математического). Рисунок 4 ­ Маятники: а) пружинный; б) математический.Вводят определение: механические колебания, которые совершаются под действием силы, пропорциональной смещению и направленной к положению равновесия, называют гармоническими.Если из динамических уравнений выразить ускорение ( и ), то может быть дано и такое определение: движение, при котором ускорение прямо пропорционально отклонению материальной точки от положения равновесия и всегда направлено в сторону равновесия, называют гармоническим колебанием.Под руководством учителя анализируют динамическое уравнение колебания маятников. Обращают внимание на общие черты этих уравнений, их внешнее сходство – уравнения и линейны, коэффициенты при координате х постоянны и не зависят ни от самой координаты, ни от ускорения.Следует обратить внимание школьников на то, что гармонические колебания ­ качественно новый вид движения, в котором ускорение непрерывно изменяется по модулю и направлению. Полезно провести анализ зависимости ускорения маятников от смещения и сравнить гармоническое колебание с уже известными учащимся видами движения – прямолинейным (равномерным и равноускоренным) и равномерным движением по окружности.При анализе уравнения (или ) обращают внимание на то, что при большой деформации пружины (или большом отклонении нити маятника от положения равновесия) нарушается прямая пропорциональность между ускорением и смещением. Постоянный коэффициент (или ) становится зависимым от деформации пружины (или угла отклонения нити), уравнение перестает быть линейным – движение будет периодическим, но не гармоническим. Таким образом, приходим к выводу: при отсутствии рассеяния энергии и достаточно малых амплитудах свободные колебания маятников являются гармоническими.Введение основных характеристик колебательного движения – амплитуды, частоты и периода – может последовать сразу после того, как рассмотрены свободные колебания маятников и введено понятие гармонического колебания. Строго говоря, понятие частоты применимо только для гармонических колебаний, т.е. для бесконечных во времени процессов. В случае периодических процессов негармонического характера (а именно с ними чаще всего приходится встречаться) мы имеем дело не с частотой, а с целым набором (полосой) частот.Вводят понятие амплитуды, частоты и периода колебаний, причем подчеркивают, что именно эти величины, а не смещение, скорость и ускорение колеблющейся точки в данный момент времени характеризуют колебательный процесс в целом. Для усвоения понятий амплитуды, периода и частоты колебаний необходимо предложить учащимся ряд упражнений различного характера – качественных, количественных, связанных с проведением экспериментов.Формулы для периода колебаний математического и пружинного маятников не могут быть строго выведены из-за отсутствия необходимой математической подготовки учащихся. Поэтому они могут быть даны в готовом виде (с последующей экспериментальной проверкой) или выведены косвенным путем.Например, формулу периода колебаний математического маятника можно получить, используя экспериментальный фат, установленный еще X. Гюйгенсом: конический маятник длиной l совершает полный оборот за тот же промежуток времени, в течение которого математический маятник той же длины совершает полное колебание, т.е. за период. Перед учащимися можно поставить задачу: воспользовавшись этим опытным фактом, найти формулу периода колебания математического маятника.Для лучшего усвоения формулы периода колебаний маятников ( и ) ее следует проверить на опыте, показав, что от коэффициента упругости и массы груза, так же как и от ускорения свободного падения и длины нити для математического маятника, зависит собственная частота колебаний системы. 1.1.2 Колебания в системах при наличии трения Наличие сил трения приводит к уменьшению энергии колебательной системы и убыванию амплитуды колебаний. Замедляя движение, силы трения увеличивают период, т.е. уменьшает частоту колебаний. Такие колебания не будут гармоническими, механическая энергия постепенно расходуется на совершение работы по преодолению силы сопротивления воздуха и превращается во внутреннюю энергию. Чем больше сила сопротивлению движению, тем быстрее прекращаются свободные колебания. В более вязких средах, например, в воде колебания затухают быстрее, чем в воздухе. Такие колебания называются затухающими.Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс в природе невозможен. Свободные колебания любого маятника рано или поздно затухают и прекращаются. Поэтому в практической деятельности обычно встречаются именно с затухающими колебаниями. Они характеризуются тем, что амплитуда колебаний xm является убывающей функцией. В реальных колебательных системах помимо возвращающей силы действуют силы сопротивления среды. Поскольку скорость движения при колебаниях небольшая, будем считать, что сила сопротивления пропорциональна скорости движения Fс

1.2 Научно-методический анализ содержания раздела «Электромагнитные колебания»

Содержание


Дифференциальное уравнение движения
Aq + c(t)q = 0
содержит переменный коэффициент и описывает параметрические колебания. Как мы увидим ниже, свойства движения, описываемого уравнением, существенно отличаются от свойств свободных колебаний, определяемых дифференциальными уравнениями с постоянными коэффициентами. Важное значение имеют нередко встречающиеся в приложениях случаи периодического изменения параметра, когда
c(t + T) = c(t).
Соответствующие этим случаям колебания называются параметрическими возбуждаемыми или, короче, параметрическими.

1.2 Научно-методический анализ содержания раздела «Электромагнитные колебания»

1.2.1 Свободные электромагнитные колебания в идеализированных колебательных системах – колебательный контур


Среди различных электрических явлений особое место занимают электромагнитные колебания, при которых электрические величины (заряды, токи) периодически изменяются и которые сопровождаются взаимными превращениями электрического и магнитного полей. Для возбуждения и поддерживания электромагнитных колебаний используется колебательный контур ­ цепь, состоящая из включенных последовательно катушки индуктивностью L, конденсатора емкостью С и резистора сопротивлением R.

Простейший электрический колебательный контур состоит из конденсатора и индуктивности соединенных между собой (рис.9). Будем считать, что емкость между витками катушки весьма мала по сравнению с емкостью конденсатора, а индуктивность конденсатора и соединительных проводов мала сравнительно с индуктивностью катушки.


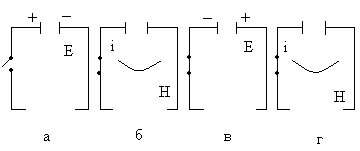
Рисунок 9 ­ Электрические колебания с индуктивностью и емкостью
Предположим, что, разомкнув контур, зарядили конденсатор. Между пластинами конденсатора появится электрическое поле, которое будет заключать в себе определенную энергию (а). Замкнем теперь конденсатор на индуктивность. Конденсатор начнет разряжаться, и его электрическое поле будет уменьшаться. При этом в контуре возникает электрический ток разряда конденсатора, отчего в катушке индуктивности появится магнитное поле. Через некоторое время, равное четверти периода колебания, конденсатор разрядится полностью, и электрическое поле исчезнет вовсе. Но магнитное поле при этом достигает максимума, а следовательно, энергия электрического поля превратится в энергию магнитного поля.


В дальнейшие моменты времени магнитное поле будет исчезать, так как не имеется токов, его поддерживающих. Это исчезающие поле вызовет самоиндукции, который в соответствии с законом Ленца будет стремиться поддерживать ток разряда конденсатора и будет, следовательно, направлен так же, как и этот последний. Поэтому конденсатор будет перезаряжаться и между его пластинами появится электрическое поле противоположного направления. Через время, равное половине периода колебания, магнитное поле исчезает вовсе, а электрическое поле достигает максимума, и энергия магнитного поля вновь превратится в энергию электрического поля. В дальнейшем конденсатор будет снова разряжаться и в контуре возникает ток, направленный противоположно току в предыдущей стадии процесса. Через время 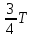конденсатор вновь окажется разряженным, а энергия электрического поля снова превратится в энергию магнитного поля (г). Через промежутки времени, равные полному периоду колебания Т, электрическое состояние контура будет таким же, как и в начале колебаний (а).

Если сопротивление контура равно нулю, то указанный процесс периодического превращения электрической энергии в магнитную и обратно будет продолжаться неограниченно долго, и мы получим незатухающие электрические колебания.

При этом изменение заряда конденсатора с течением времени выражалось бы кривой (а. рис.10), которая есть синусоида. По такому закону изменялось бы и напряжение на конденсаторе и сила тока в контуре и колебания были бы гармоническими.


Рисунок 10 - Затухание электрических колебаний
В действительности же сопротивление контура всегда не равно нулю. Вследствие этого энергия, первоначально запасенная в контуре, непрерывно расходуется на выделение тепла Ленца - Джоуля, так что интенсивность электрических колебаний постепенно уменьшается, и в конце концов колебания прекращаются вовсе. Поэтому на экране осциллографа мы видим кривую (б) затухающие электромагнитные колебания. Если увеличить сопротивление контура, то затухание колебаний увеличивается (в).

В связи с изложенным отметим, что периодическими называется такие процессы, в которых изменяющиеся физические величины через определенные промежутки времени принимают одинаковые значения:

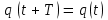
Так, гармонические колебания, изображаемые кривой (а), есть периодический процесс, имеющий совершенно определенный конечный период Т. Напротив, затухающие колебания, изображаемые кривыми б и в на рис.10, не имеют конечного периода (Т = ∞) и поэтому, строго говоря, не является периодическим процессом. Тем не менее, если затухание мало, небольшой отрезок кривых б и в можно приближенно рассматривать как отрезок соответствующей синусоиды и говорить о затухающих колебаниях как о гармонических колебаниях, амплитуда которых постепенно уменьшается.

Для количественной характеристики затухание пользуется тем, что отношение двух последовательных амплитуд qn и qn+1 на рис. 10б остается постоянным в течение всего процесса. Натуральный логарифм этого отношения принимают за меру затухания колебаний и называют логарифмическим затуханием.

Если постепенно увеличивать сопротивление контура r, то затухание колебаний увеличивается и логарифмически растет.

Когда сопротивление превышает некоторое определенное для данного контура значение rк, колебания не возникают вовсе и разряд описывается кривой (г). В этом случае заряд конденсатора уменьшается монотонно, сначала медленно, а затем с большей скоростью, и асимптотически стремится к нулю. При дальнейшем увеличении сопротивления эта кривая постепенно переходит в кривую (д).

Сопротивление r k называется критическим сопротивлением контура. Оно зависит от величины емкости и индуктивности контура. Для возможности электрических колебаний, следовательно, необходимо, чтобы сопротивление контура r было меньше r k. При r > rk имеем апериодический разряд.

Отметим, что рассмотренные особенности разряда в электрическом колебательном контуре совершенно аналогичны особенностям механической колебательной системы, обладающей трением.

Механические колебания, возникающие под действием сил, развивающихся в самой колебательной системе, называются собственными колебаниями. Они возникают при всяком нарушении равновесия колебательной системы. Подобно этому, электрические колебания, происходящие под действием процессов в самом колебательном контуре, получили название собственных электрических колебаний.

Пользуясь аналогией между механическими и электрическими колебаниями, можно просто вычислить период электрических колебаний, не прибегая к точной теории. Из механики известно, что период колебаний груза на пружине выражается формулой:



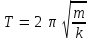
где m – масса груза, а k – упругость пружины. В случае электрических колебаний роль массы играет индуктивность L, а роль упругости – величина, обратная емкости, т. е 1/C. Если мы заменим m на L, а k на 1/C, находим:


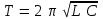
Видно если изменять емкость конденсатора или величину индуктивности, можно легко продемонстрировать влияние L и C на период колебаний.

1.2.2 Электромагнитные колебания в реальном колебательном контуре


Реальный колебательный контур обладает активным сопротивлением, поэтому при воздействии в контуре свободных колебаний энергия предварительно заряженного конденсатора постепенно тратится, преобразуясь в тепловую.

Свободные колебания в контуре являются затухающими, так как в каждый период энергия уменьшается и амплитуда колебаний в каждый период будет уменьшаться.



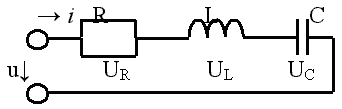
Рисунок 11­ реальный колебательный контур.

Угловая частота свободных колебаний в реальном колебательном контуре :



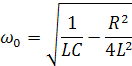
Если R=2… , то угловая частота равна нулю, следовательно свободные колебания в контуре не возникнут.

Таким образом колебательным контуром называется электрическая цепь состоящая из индуктивности и емкости и обладающая малым активным сопротивлением, меньшим удвоенного характеристического сопротивления, что обеспечивает обмен энергией между индуктивностью и емкостью.

В реальном колебательном контуре свободные колебания затухают тем быстрее, чем больше активное сопротивление.

Для характеристики интенсивности затухания свободных колебаний используется понятие «затухание контура» - отношение активного сопротивления к характеристическому.



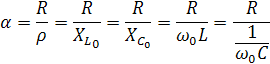
На практике используют величину, обратную затуханию – добротность контура.



Для получения незатухающих колебаний в реальном колебательном контуре необходимо в течение каждого периода колебаний пополнять электрическую энергию на активном сопротивлении контура в такт с частотой собственных колебаний. Это осуществляется с помощью генератора.


Если подключить колебательный контур к генератору переменного тока, частота которого отличается от частоты свободных колебаний контура, то в цепи протекает ток с частотой равной частоте напряжения генератора. Эти колебания называют вынужденным.

Если частота генератора отличается от собственной частоты контура, то такой колебательный контур является ненастроенным относительно частоты внешнего воздействия, если же частоты совпадают, то настроенным.

1.2.3 Вынужденные электромагнитные колебания в реальных системах. Электрический резонанс



В данном разделе ограничимся только цепями с сосредоточенными емкостями и индуктивностями и будем считать переменные токи. Иными словами, будем предполагать, что время τ, в течение которого электрические величины принимают установившиеся значения, мало по сравнению с периодом колебаний Т, и поэтому будем применять к мгновенным значениям всех электрических величин законы постоянного тока.

Далее, мы будем рассматривать только такие токи, сила которых меняется по синусоидальному закону:

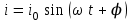
Это объясняется несколькими причинами. Во-первых, как мы знаем все технические генераторы переменных токов, имеют ЭДС, изменяющуюся по закону, очень близкому к синусоидальному, и потому создаваемые ими токи практически являются синусоидальными. Вторая причина заключается в том, что теория синусоидальных токов особенно проста и вследствие этого на примере таких токов можно особенно просто выяснить основные особенности электрических колебаний.

Электрические лампы в наших квартирах и на улице, холодильник и пылесос, телевизор и магнитофон работают, используя энергию электромагнитных колебаний.

На применении электромагнитных колебаний основана работа электромоторов, приводящих в действие станки на заводах и фабриках, движущих электровозы.

Во всех этих примерах речь идет об использовании переменного электрического тока. Переменный электрический ток в энергетических электрических цепях является результатом возбуждения в них вынужденных электромагнитных колебаний. Эти вынужденные колебания создаются генераторами переменного тока, работающими на электростанциях.

Переменный ток – это по существу вынужденные колебания электрических зарядов в проводнике под действием приложенной переменной ЭДС.

При механических колебаниях резонанс выражен отчетливо при малых значениях коэффициента трения μ. В электрической цепи роль коэффициента трения играет активное сопротивление R. Ведь именно наличие этого сопротивления в цепи приводит к прекращению энергии тока во внутреннюю энергию проводника. Поэтому резонанс в электрическом колебательном контуре должен быть выражен отчетливо при малом активном сопротивлении R.

Смотрите также файлы