Файл: Контрольная работа Использование моделей в процессе обучения детей дошкольного возраста решению арифметических задач по методике Н. Ю. Непомнящей.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 104
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
< и обращает внимание детей на различия в их начертаниях: вершина угла всегда смотрит на меньшее. Затем дети упражняются в использовании знаков при сравнении целого и частей.
После того, как дошкольников ознакомили с операцией объединения частей в целое, их обучают удалению из целого его части и графическому изображению данного действия. Например, на картине, висящей на доске, нарисовано дерево, на котором приютились воробьи и вороны. Дети рассказывают, что они видят. (На дереве птицы, но часть из них воробьи, а часть вороны.) Воробьи улетают, на дереве остаются одни вороны. «Как это изобразить в виде целого и частей?» спрашивает педагог. Сначала дети рисуют целое. «Что же произошло?» - спрашивает воспитатель и предлагает рассказать об этом. «На дереве сидели птицы: воробьи и вороны; воробьи улетели, остались только вороны», - говорят дети. На занятии рассматривается ряд подобных ситуаций, а затем делается обобщение: «Если из целого, состоящего из двух частей, удалить одну часть, то целое уменьшится, в нем останется только одна часть». Затем дети думают, как это можно изобразить, и приходят к выводу, что надо зачеркнуть в объединенном целом одну часть.
В дальнейшем детей упражняют в умении самостоятельно определить, какая операция с совокупностями (объединение или удаление части) может быть выполнена. Для этого детям предлагаются различные сюжетные картинки. Ребята получают задание рассказать, какое действие с совокупностями можно произвести по той или иной картинке и как изобразить это графически.
Для закрепления полученных знаний детям предлагают: составить целое из разных частей (цветов, видов транспорта, животных, игрушек, мебели, посуды), изобразить это графически, из составленного целого удалить одну из его частей и тоже изобразить графически.
Итак, на первом этапе обучении решению простых задач детей знакомят с понятием целого, которое отражает величину совокупности предметов, учат видеть структуру целого, по отношению к частям; дети практически усваивают операции объединения совокупностей и удаления части из целого. Это позволяет в дальнейшем понять сущность арифметических действий сложения и вычитании, связь между компонентами этих действий и их результатом, а также связь между самими действиями сложения и вычитания. Учитывая особенности детского мышления, в обучении дошкольников следует использовать моделирующие движения, диаграммы, условные знаки и обозначения.
На втором этапе обучения раскрываются связи между данными и искомым, на основе чего выбирается, а затем выполняется арифметическое действие и находится ответ задачи. Для записи арифметических действий вводятся условные обозначения плюс (+), минус (—), равно (=).
Для введения знаков сложения и вычитания и моделирования соответствующего арифметического действия предлагается следующая ситуация: по картинке (с ярко выраженным действием объединения двух совокупностей) рассказать о ее содержании и об операциях с совокупностями, а потом изобразить отношения между ними в виде диаграммы. Педагог объясняют, что эту операцию можно не только зарисовать, но и записать знаками. «У вас на столе лежат разные геометрические фигуры и арифметические знаки плюс (+), равно (=), круг, полукругии др.». (Эти знаки изображены на карточках из картона.) Детей знакомят с ними, показывают, что из двух полукругов можно составить целый круг, объясняют, как при помощи этих знаков можно записать то, что изображено окружностями.
+ =
После ознакомления со знаками детям предлагают составить рассказ по сюжетной картинке и изобразить окружностями объединение совокупностей, а затем составить модель записи действия. Например, в составленном букете цветов имеются две части: ромашки и васильки. Детей подводят к выводу: если к половине круга прибавить еще такую же половину, то обе половины будут равны кругу
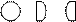Так же объясняют и запись операции удаления части из целого: если из букета (целого) удалить его часть, то другая часть останется в букете. Это удаление можно выразить, а затем записать модель арифметического действия
– =
Подобное моделирование записи арифметического действия вычитания демонстрирует удаление части из целого. На начальном этапе обучения дошкольников моделированию записи арифметического действия совокупности даются равными, чтобы не вызвать у детей сомнения. После того как дети овладевают основным смыслом моделированной записи, их внимание обращается на то, что части по количеству элементов могут быть разными, например: в букете может быть 6 васильков, а ромашек 4. Запись остается такой же, а более точное количество васильков и ромашек, так же как и их сумма, записывается соответствующими цифрами. Так под условной моделью появляется запись арифметическою действия - числового равенства:
+ =
6 + 4 = 10
В процессе изучения записи в виде модели арифметического действия детям предлагаются такие вопросы: «Что обозначает целый круг? Что обозначают первый и второй полукруги? О чем говорит тот или иной арифметический знак (плюс, минус, равно)? Почему в целом зачеркнута одна часть?» Подобная подготовка подводит дошкольников к пониманию подлинного смысла самого арифметического действия и структуры арифметической задачи.
Для ознакомления детей с составными частями задачи (условием и вопросом), предлагается следующая ситуация: по картинке дети составляют задачу, графически изображая объединение совокупностей. Воспитатель по данному графическому изображению повторяет составленную детьми задачу, делает паузу между условием и вопросом, подчеркивая при этом, что в задаче есть известные числа, а вопрос направлен на выяснение неизвестного. Затем дети определяют количество частей в задаче, раздельно повторяя каждую из них, после чего воспитатель объясняет: та часть задачи, в которой говорится об известных числах, называется условием задачи, а вопрос направлен на выяснение неизвестного, т.е. того, что следует еще узнать.
Далее детям предлагается сравнить задачу с рассказом или загадкой. Делается общий вывод о том, что темой условия задачи может быть все происходящее вокруг, но обязательно с указанием количества предметов совокупности. Вопрос же задачи направлен на то, чтобы произвести то или иное арифметическое действие с указанными в условии задачи числами: или их объединить, т.е. произвести действие сложения, или из большего числа вычесть меньшее число, как бы удалить из целого его часть, т.е. произвести вычитание.
После этого выполняются упражнения на составление задач, графическое их изображение, запись моделируемого действия, а затем и запись арифметического действия, т.е. числового равенства. Для того чтобы знать и четко различать известное и неизвестное, воспитатель договаривается с детьми о том, что известные совокупности, о которых говорится в условии задачи, они обведут на картинке черными шнурками в виде окружности, а неизвестную совокупность, о которой спрашивается в вопросе, - красным шнурком. Точно так же и при графическом изображении известные совокупности обведут черным, а неизвестные - красным карандашом. Так с помощью значков дети приучаются отличать известное от неизвестного.
Дошкольникам показывают образец анализа картинки. Затем они по картинкам разного содержания, но с ярко выраженным действием (объединение групп предметов или удаление части предметов из группы) самостоятельно учатся составлять задачи, графически зарисовывать и записывать числовые выражения и равенства.
Например, детям предлагается картинка с изображением ведерка, на стол кладется набор карточек с изображением рыб. Воспитатель сообщает текст задачи: «Мальчик поймал 4 окуня и 1 ерша. (Показывает их и опускает в ведерко.) Сколько рыб поймал мальчик?» Детей просят повторить задачу: «О чем говорится в задаче? Что нам известно? Изобразим это с помощью цветных кругов, арифметических знаков и значков». (Дети повторяют задачу, выполняют диаграмму, записывают модель действия сложения.) Воспитатель продолжает: «Если известно, что мальчик поймал 4 окуня и 1 ерша, то, как узнать, сколько всего рыб поймал мальчик? (Обводит красным карандашом окружность.) Каким действием решается задача?» Педагог выслушивает ответы детей и дает образец формулировки арифметического действия: «Чтобы узнать, сколько рыб поймал мальчик, надо к 4 прибавить 1. Сколько получится?» Решение записывается с помощью готовых карточек с изображением цифр и знаков: 4 + 1 = 5.
Воспитатель сообщает, что всего мальчик поймал 5 рыб и спрашивает: Каким действием решается задача? Дети отвечают, что задача решается действием сложения. Затем ребята поясняют, что обозначает каждый значок и окружность красного цвета. Количество предметов, известных из задачи, обозначается черными окружностями, а количество предметов искомого, неизвестной совокупности, о которой спрашивается в задаче, - красной окружностью. Так с помощью значков дети приучаются отличать известное от неизвестного.
Аналогично рассматривается ситуация удаления части из целого.
С помощью таких заданий можно упражнять детей в нахождении неизвестного первого (второго) слагаемого, нахождении уменьшаемого или вычитаемого.
Например, вывешивается диаграмма (рис. 2). У детей спрашивают: «Что на ней изображено, что принято за известное и что за неизвестное, какую задачу можно составить no этой диаграмме? Каким действием она будет решаться?» Детям необходимо сформулировать его и составить числовое равенство. Так же выполняется задание по диаграмме, изображающей операцию удаления части из целого (рис. 3).
Рис. 2 Рис. 3
В дальнейшем неизвестным становится первое или второе слагаемое, диаграмма и запись выглядят так, как изображено на рис. 4.
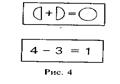
Дети могут составлять задачи по готовым диаграммам. При этом ставятся вопросы: «Какое целое изображено? (Например, неизвестное.) Сколько в нем частей? (Две.) Какие это части? (Например, известные: одно - 3 предмета, а другое - 2 предмета.) Какое действие нужно совершить? (Действие сложения.) (Предлагается записать или подобрать его модель.) Какое же здесь должно быть числовое равенство? Запишите его». Аналогично составляют задачи на вычитание.
В тех случаях, когда предлагается составить задачу по предъявленной модели записи действия, детей спрашивают: «Какое действие изображено на этой карточке? Подумай, составь задачу, изобрази ее с помощью кругов и запиши арифметическое действие». Приведем пример. Дается модель:
+ =
«Какое это действие? Что обозначает большой круг? Какую задачу можно составить по этой карточке?» Дети должны придумать задачу на нахождение неизвестного уменьшаемого. «На шнурке висели бусы, 2 бусинки упали, а 6 осталось. Сколько бусинок было на шнурке?» Дошкольники изображают диаграмму с помощью окружностей и записывают числовое равенство: 6 + 2 = 8.
Так, опираясь на наглядный материал, можно научить детей выделять данные и искомое, составлять и решать задачи на нахождение суммы, остатка, неизвестных компонентов действий сложения и вычитания.
В процессе обучения детей можно ознакомить с алгоритмом решения задачи:
1. Выделить в задаче части и целое.
2. Построить диаграмму.
3. Определить, что неизвестно – часть или целое.
4. Определить действие, которым решается задача, по правилу: Если неизвестно целое, то задача решается сложением. Если неизвестна часть, то вычитанием.
5.Записать решение.
6. Назвать ответ.
После того, как дошкольников ознакомили с операцией объединения частей в целое, их обучают удалению из целого его части и графическому изображению данного действия. Например, на картине, висящей на доске, нарисовано дерево, на котором приютились воробьи и вороны. Дети рассказывают, что они видят. (На дереве птицы, но часть из них воробьи, а часть вороны.) Воробьи улетают, на дереве остаются одни вороны. «Как это изобразить в виде целого и частей?» спрашивает педагог. Сначала дети рисуют целое. «Что же произошло?» - спрашивает воспитатель и предлагает рассказать об этом. «На дереве сидели птицы: воробьи и вороны; воробьи улетели, остались только вороны», - говорят дети. На занятии рассматривается ряд подобных ситуаций, а затем делается обобщение: «Если из целого, состоящего из двух частей, удалить одну часть, то целое уменьшится, в нем останется только одна часть». Затем дети думают, как это можно изобразить, и приходят к выводу, что надо зачеркнуть в объединенном целом одну часть.
В дальнейшем детей упражняют в умении самостоятельно определить, какая операция с совокупностями (объединение или удаление части) может быть выполнена. Для этого детям предлагаются различные сюжетные картинки. Ребята получают задание рассказать, какое действие с совокупностями можно произвести по той или иной картинке и как изобразить это графически.
Для закрепления полученных знаний детям предлагают: составить целое из разных частей (цветов, видов транспорта, животных, игрушек, мебели, посуды), изобразить это графически, из составленного целого удалить одну из его частей и тоже изобразить графически.
Итак, на первом этапе обучении решению простых задач детей знакомят с понятием целого, которое отражает величину совокупности предметов, учат видеть структуру целого, по отношению к частям; дети практически усваивают операции объединения совокупностей и удаления части из целого. Это позволяет в дальнейшем понять сущность арифметических действий сложения и вычитании, связь между компонентами этих действий и их результатом, а также связь между самими действиями сложения и вычитания. Учитывая особенности детского мышления, в обучении дошкольников следует использовать моделирующие движения, диаграммы, условные знаки и обозначения.
На втором этапе обучения раскрываются связи между данными и искомым, на основе чего выбирается, а затем выполняется арифметическое действие и находится ответ задачи. Для записи арифметических действий вводятся условные обозначения плюс (+), минус (—), равно (=).
Для введения знаков сложения и вычитания и моделирования соответствующего арифметического действия предлагается следующая ситуация: по картинке (с ярко выраженным действием объединения двух совокупностей) рассказать о ее содержании и об операциях с совокупностями, а потом изобразить отношения между ними в виде диаграммы. Педагог объясняют, что эту операцию можно не только зарисовать, но и записать знаками. «У вас на столе лежат разные геометрические фигуры и арифметические знаки плюс (+), равно (=), круг, полукругии др.». (Эти знаки изображены на карточках из картона.) Детей знакомят с ними, показывают, что из двух полукругов можно составить целый круг, объясняют, как при помощи этих знаков можно записать то, что изображено окружностями.+ =
После ознакомления со знаками детям предлагают составить рассказ по сюжетной картинке и изобразить окружностями объединение совокупностей, а затем составить модель записи действия. Например, в составленном букете цветов имеются две части: ромашки и васильки. Детей подводят к выводу: если к половине круга прибавить еще такую же половину, то обе половины будут равны кругу
Так же объясняют и запись операции удаления части из целого: если из букета (целого) удалить его часть, то другая часть останется в букете. Это удаление можно выразить, а затем записать модель арифметического действия– =
Подобное моделирование записи арифметического действия вычитания демонстрирует удаление части из целого. На начальном этапе обучения дошкольников моделированию записи арифметического действия совокупности даются равными, чтобы не вызвать у детей сомнения. После того как дети овладевают основным смыслом моделированной записи, их внимание обращается на то, что части по количеству элементов могут быть разными, например: в букете может быть 6 васильков, а ромашек 4. Запись остается такой же, а более точное количество васильков и ромашек, так же как и их сумма, записывается соответствующими цифрами. Так под условной моделью появляется запись арифметическою действия - числового равенства:
+ =6 + 4 = 10
В процессе изучения записи в виде модели арифметического действия детям предлагаются такие вопросы: «Что обозначает целый круг? Что обозначают первый и второй полукруги? О чем говорит тот или иной арифметический знак (плюс, минус, равно)? Почему в целом зачеркнута одна часть?» Подобная подготовка подводит дошкольников к пониманию подлинного смысла самого арифметического действия и структуры арифметической задачи.
Для ознакомления детей с составными частями задачи (условием и вопросом), предлагается следующая ситуация: по картинке дети составляют задачу, графически изображая объединение совокупностей. Воспитатель по данному графическому изображению повторяет составленную детьми задачу, делает паузу между условием и вопросом, подчеркивая при этом, что в задаче есть известные числа, а вопрос направлен на выяснение неизвестного. Затем дети определяют количество частей в задаче, раздельно повторяя каждую из них, после чего воспитатель объясняет: та часть задачи, в которой говорится об известных числах, называется условием задачи, а вопрос направлен на выяснение неизвестного, т.е. того, что следует еще узнать.
Далее детям предлагается сравнить задачу с рассказом или загадкой. Делается общий вывод о том, что темой условия задачи может быть все происходящее вокруг, но обязательно с указанием количества предметов совокупности. Вопрос же задачи направлен на то, чтобы произвести то или иное арифметическое действие с указанными в условии задачи числами: или их объединить, т.е. произвести действие сложения, или из большего числа вычесть меньшее число, как бы удалить из целого его часть, т.е. произвести вычитание.
После этого выполняются упражнения на составление задач, графическое их изображение, запись моделируемого действия, а затем и запись арифметического действия, т.е. числового равенства. Для того чтобы знать и четко различать известное и неизвестное, воспитатель договаривается с детьми о том, что известные совокупности, о которых говорится в условии задачи, они обведут на картинке черными шнурками в виде окружности, а неизвестную совокупность, о которой спрашивается в вопросе, - красным шнурком. Точно так же и при графическом изображении известные совокупности обведут черным, а неизвестные - красным карандашом. Так с помощью значков дети приучаются отличать известное от неизвестного.
Дошкольникам показывают образец анализа картинки. Затем они по картинкам разного содержания, но с ярко выраженным действием (объединение групп предметов или удаление части предметов из группы) самостоятельно учатся составлять задачи, графически зарисовывать и записывать числовые выражения и равенства.
Например, детям предлагается картинка с изображением ведерка, на стол кладется набор карточек с изображением рыб. Воспитатель сообщает текст задачи: «Мальчик поймал 4 окуня и 1 ерша. (Показывает их и опускает в ведерко.) Сколько рыб поймал мальчик?» Детей просят повторить задачу: «О чем говорится в задаче? Что нам известно? Изобразим это с помощью цветных кругов, арифметических знаков и значков». (Дети повторяют задачу, выполняют диаграмму, записывают модель действия сложения.) Воспитатель продолжает: «Если известно, что мальчик поймал 4 окуня и 1 ерша, то, как узнать, сколько всего рыб поймал мальчик? (Обводит красным карандашом окружность.) Каким действием решается задача?» Педагог выслушивает ответы детей и дает образец формулировки арифметического действия: «Чтобы узнать, сколько рыб поймал мальчик, надо к 4 прибавить 1. Сколько получится?» Решение записывается с помощью готовых карточек с изображением цифр и знаков: 4 + 1 = 5.
Воспитатель сообщает, что всего мальчик поймал 5 рыб и спрашивает: Каким действием решается задача? Дети отвечают, что задача решается действием сложения. Затем ребята поясняют, что обозначает каждый значок и окружность красного цвета. Количество предметов, известных из задачи, обозначается черными окружностями, а количество предметов искомого, неизвестной совокупности, о которой спрашивается в задаче, - красной окружностью. Так с помощью значков дети приучаются отличать известное от неизвестного.
Аналогично рассматривается ситуация удаления части из целого.
С помощью таких заданий можно упражнять детей в нахождении неизвестного первого (второго) слагаемого, нахождении уменьшаемого или вычитаемого.
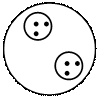
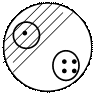
Например, вывешивается диаграмма (рис. 2). У детей спрашивают: «Что на ней изображено, что принято за известное и что за неизвестное, какую задачу можно составить no этой диаграмме? Каким действием она будет решаться?» Детям необходимо сформулировать его и составить числовое равенство. Так же выполняется задание по диаграмме, изображающей операцию удаления части из целого (рис. 3).
| | | | |
| |  | |  |
| | | | |
Рис. 2 Рис. 3
В дальнейшем неизвестным становится первое или второе слагаемое, диаграмма и запись выглядят так, как изображено на рис. 4.
| | | |
| |  | |
Дети могут составлять задачи по готовым диаграммам. При этом ставятся вопросы: «Какое целое изображено? (Например, неизвестное.) Сколько в нем частей? (Две.) Какие это части? (Например, известные: одно - 3 предмета, а другое - 2 предмета.) Какое действие нужно совершить? (Действие сложения.) (Предлагается записать или подобрать его модель.) Какое же здесь должно быть числовое равенство? Запишите его». Аналогично составляют задачи на вычитание.
В тех случаях, когда предлагается составить задачу по предъявленной модели записи действия, детей спрашивают: «Какое действие изображено на этой карточке? Подумай, составь задачу, изобрази ее с помощью кругов и запиши арифметическое действие». Приведем пример. Дается модель:
+ =
«Какое это действие? Что обозначает большой круг? Какую задачу можно составить по этой карточке?» Дети должны придумать задачу на нахождение неизвестного уменьшаемого. «На шнурке висели бусы, 2 бусинки упали, а 6 осталось. Сколько бусинок было на шнурке?» Дошкольники изображают диаграмму с помощью окружностей и записывают числовое равенство: 6 + 2 = 8.
Так, опираясь на наглядный материал, можно научить детей выделять данные и искомое, составлять и решать задачи на нахождение суммы, остатка, неизвестных компонентов действий сложения и вычитания.
В процессе обучения детей можно ознакомить с алгоритмом решения задачи:
1. Выделить в задаче части и целое.
2. Построить диаграмму.
3. Определить, что неизвестно – часть или целое.
4. Определить действие, которым решается задача, по правилу: Если неизвестно целое, то задача решается сложением. Если неизвестна часть, то вычитанием.
5.Записать решение.
6. Назвать ответ.