2. 
   Задачи регрессионного анализа
   

Выделяются различные формальные задачи регрессионного анализа. Они могут бы ть простыми или сложными по формулировкам, по математическим средствам и трудоемкости. Перечислим и рассмотрим на примерах те из них, которые представляются основными.

Первая задача – выявить факт изменчивости изучаемого явления при определенных, но не всегда четко фиксированных условиях.

Вторая задача – выявить тенденцию как периодическое изменение признака.

Третья задача – это выявление закономерности, выраженной в виде корреляционного уравнения (регрессии). Линейная модель парной регрессии Регрессия – функция, позволяющая по величине одного корреллируемого признака определить среднюю величину другого признака.

2. 
   Этапы регрессионного анализа
   

Выделим основные этапы регрессионного анализа.

Первый этап. Предположение. На этом этапе происходит выбор формы связи между переменными (модель).

Второй этап. Параметризация – происходит оценка значений параметра в выбранной формуле статистической связи. Форма связи (функция) линейная, нелинейная.

Третий этап. Проверка надёжности полученных оценок. На этом этапе осуществляются следующие тесты: F-тест (проверка статистической значимости выбранной формы связи), t-тест (проверка статистической значимости найденных числовых значений параметра). В результате анализа статистических данных, выбора и построения модели последовательно выполняются все три этапа. Формально могут возникать ситуации двух типов:

1. Вид функциональной зависимости неизвестен. В этом случае нужно решить предварительно задачу, направленную на отыскание подходящей функциональной зависимости. Это достаточно сложная задача, но она успешно решается современными средствами информационных технологий (программа Excel).

2.Вид функциональной зависимости известен и требуется только найти ее параметры (коэффициенты регрессии b 0 , b 1 , b 2 , …). Термином линейный регрессионный анализ обозначают такое прогнозирование, которое описывается линейной взаимосвязью между исследуемыми переменными: y = b0 + b1x.

При всем разнообразии эмпирических формул все же имеется вид аналитической зависимости, получивший широкое распространение. Им является уравнение регрессии в виде многочленов (полинома), расположенных по восходящим степеням изучаемого фактора и одновременно линейных ко всем коэффициентам.

---

Такая формула имеет вид:
y = f(x) = b0 + b1x + b2x2 +…+bm ,
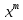где b0 , b1 , b2 ,…, bm − коэффициенты, подлежащие определению.

Этот ряд − сходящийся, т.к. стремится к некоторому пределу.

Эмпирические формулы (аппроксимирующие уравнения) всегда имеют ограниченную область применения, которая не должна выходить за пределы имеющихся опытных данных.

Широкое применение аппроксимирующих уравнений объясняется следующими причинами:

1. Точное аналитическое выражение зависимости между исследуемыми величинами может оставаться неизвестным и поэтому по необходимости приходится ограничиваться приближенными формулами эмпирического характера.

2. Точная функциональная зависимость выражается формулой настолько сложной, что ее непосредственное применение при вычислениях было бы очень затруднительным.

Эмпирические формулы могут быть разнообразными, т.к. при выборе аналитической зависимости руководствуются не какими-то строгими теориями (физическими или экономическими), а ставят только одно условие −возможно близкое соответствие значений, вычисленных по формуле опытным данным. Таким образом, формально описание одного и того же процесса можно дать разными по виду уравнениями. Их пригодность оценивается только по одному критерию − наиболее точное предсказание экспериментального результата.

В эмпирическую формулу можно вводить различное число постоянных параметров (коэффициентов), величину которых нужно определить с большой точностью. Более удачными (удобными) следует считать уравнения с небольшим числом коэффициентов (не более 2−3). В противном случае возрастают трудности с применением таких формул.


2.4 Метод наименьших квадратов
Для определения коэффициентов уравнения регрессии b применяют разные методы (графический, метод средних), однако наибольшее распространение получил метод наименьших квадратов (МНК).

Экспериментальные данные о значениях переменных х и у приведены в таблице

	i=1	i=2	i=3	i=4	i=5
xi	0	1	2	4	5
yi	2,1	2,4	2,6	2,8	3,0

---

В результате их выравнивания получена функция

Используя метод наименьших квадратов , аппроксимировать эти данные линейной зависимостью y=ax+b (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные.

Суть метода наименьших квадратов

Задача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных а и b

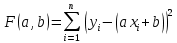
принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов.

Таким образом, решение примера сводится к нахождению экстремума функции двух переменных.

Заключение

Любой показатель практически зависит от бесконечного количества факторов. Однако лишь ограниченное количество факторов действительно существенно воздействуют на исследуемый показатель. Доля влияния остальных факторов столь незначительна, что их игнорирование не может привести к существенным отклонениям в поведении исследуемого объекта. Выделение и учет в модели лишь ограниченного числа реально доминирующих факторов является важной задачей качественного анализа, прогнозирования и управления ситуаций.

     Если  в естественных науках большей частью имеют дело со строгими (функциональными) зависимостями, при которых  каждому значению одной переменной соответствует единственное значение другой, то между экономическими переменными, в большинстве случаев, таких зависимостей нет и дело имеют с корреляционными зависимостями.

    Корреляционно-регрессионные  модели, какими бы сложными они не были, не скрывают полностью всех причинно-следственных связей, однако достаточно адекватно могут описывать влияние на результативный признак существенных факторов, если проведен предварительный анализ сущности и специфики исследуемых явлений и процессов.

     Таким образом, корреляционный и регрессионный анализ позволяет определить зависимость между факторами, а так же проследить влияние задействованных факторов. Эти показатели имеют широкое применение в обработке статистических данных

---

Список используемых источников

1. 
   Н.Ш. Кремер. Теория вероятностей и математическая статистика. - М.:2000г
   
2. 
   Пугачёв В.С., «Теория вероятностей и математическая статистика», –
   

     М.: «Инфра–М», 2004.

3. 
   Замков О.О., Толстопятенко А.В., Черемных Р.Н., «Математические
   

     методы в экономике», – М.: «Дис», 2003;

---

Смотрите также файлы

• 1. Форма отображения перечня назначений.pdf

• Фио студента Группа Для выполнения задания ответьте на вопросы теста Синдром боли в левой половине грудной клетки, расположенного на портале..docx

• Геометриялы есептерді шыаруа йрету.docx

• Зертханалы жмыс 3 Таырып.docx

• Ответ продольная волна, распространяющая вдоль контактной (иили донной) поверхности контролируемого(ой)элемента (среды), и сопутствующие ей боковые (продольная и поперечная) волны.docx