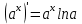Файл: Учебнометодическое пособие по курсу высшая математика часть 1 для студентов Центра заочного образования по программе.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 216
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
3. По получении из института прорецензированной работы студент обязан выполнить указания, сделанные рецензентом. В случае, если контрольная работа не зачтена, студент обязан в этой же тетради (после заключения рецензента) внести все исправления, решить заново задачи, указанные рецензентом, и представить работу на повторную рецензию.
4. Контрольная работа выполняется самостоятельно.
5. В конце работы указывается использованная литература.
6. Контрольная работа подписывается с указанием даты выполнения.
7. Контрольные работы, выполненные без соблюдения изложенных выше правил или по чужому варианту, не зачитываются и возвращаются.
5. Сдача экзаменов
К сдаче экзаменов допускаются студенты, имеющие выполненную и зачтенную контрольную работу. Экзамен сдается устно.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО РАЗДЕЛАМ КУРСА
Внимание!
Данные методические указания предназначены для краткого ознакомления с дисциплиной «Высшая математика». В них приведены теоретические результаты без доказательства и рассмотрены примеры решения задач, подобных задачам, содержащихся в контрольной работе. При изучения дисциплины «Высшая математика» кроме данного пособия необходимо использовать для самостоятельной работы литературу из списка, приведенного на стр. 5-6.
Раздел 1 Теория пределов, непрерывность функций
Не касаясь строгого определения предела, приведем здесь лишь смысл этого понятия.
Пусть задана некоторая функция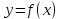 , определенная в окрестности точки
, определенная в окрестности точки 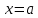 , кроме, быть может, самой точки. Пределом функции
, кроме, быть может, самой точки. Пределом функции 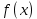 при
при 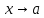 называется число
называется число 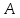 , к которому стремится функция, при приближении аргумента
, к которому стремится функция, при приближении аргумента 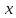 к числу
к числу 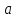 :
:
.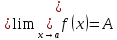
.
При вычислении предела первое, что надо сделать – подставить в выражение функции. Если указанное значение аргумента функции принадлежит области ее определения, то в результате получится некое число
в выражение функции. Если указанное значение аргумента функции принадлежит области ее определения, то в результате получится некое число 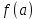 , которое и является пределом функции при
, которое и является пределом функции при  .
.
Однако, в некоторых случаях при подстановке в формулу появляется так называемая неопределенность, которая символически записывается в одном из следующих видов:
в формулу появляется так называемая неопределенность, которая символически записывается в одном из следующих видов: 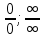 или
или 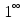 . В этом случае необходимо применять специальные методы вычисления пределов, называемые методами раскрытия неопределенностей. Также необходимо рассмотреть методы вычисления пределов функций при
. В этом случае необходимо применять специальные методы вычисления пределов, называемые методами раскрытия неопределенностей. Также необходимо рассмотреть методы вычисления пределов функций при 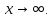
Задача 1.1. Найти предел: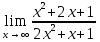
Решение. Убеждаемся, что при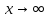 числитель и знаменатель выражения стремятся к бесконечности, и получаем неопределенность вида
числитель и знаменатель выражения стремятся к бесконечности, и получаем неопределенность вида 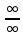 . Делим числитель и знаменатель рациональной дроби на переменную в наивысшей степени, то есть, в данном случае, на
. Делим числитель и знаменатель рациональной дроби на переменную в наивысшей степени, то есть, в данном случае, на 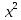 . Учитывая, что
. Учитывая, что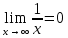 и
и 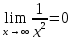 , а также используя ряд свойств пределов, получаем:
, а также используя ряд свойств пределов, получаем:
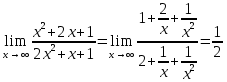 .
.
Задача 1.2. Найти предел:
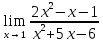
Решение. В первую очередь подставим в выражение функции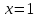 и убедимся, что данном случае мы имеем дело с неопределенностью вида
и убедимся, что данном случае мы имеем дело с неопределенностью вида 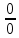 . Далее используем метод разложения трехчлена на множители, а именно:
. Далее используем метод разложения трехчлена на множители, а именно:
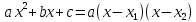
, где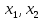 - корни квадратного трехчлена. Учитывая, что корни знаменателя
- корни квадратного трехчлена. Учитывая, что корни знаменателя 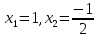 , а корни знаменателя
, а корни знаменателя 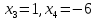 , представим исходный предел в виде:
, представим исходный предел в виде:
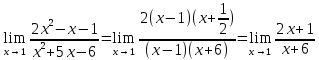 .
.
Заметим, что вместе с сокращением в числителе и знаменателе множителя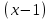 , из выражения уходит неопределенность. Теперь в выражение под знаком предела можно подставить
, из выражения уходит неопределенность. Теперь в выражение под знаком предела можно подставить  и получить, что данный предел равен
и получить, что данный предел равен 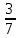 .
.
Ответ: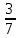 .
.
Задача 1.3. Найти предел:
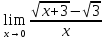 .
.
Решение. Подставляем данное выражение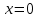 и получаем неопределенность вида
и получаем неопределенность вида 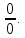
Выражения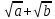 называется для выражения
называется для выражения 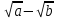 сопряженным, а его умножение на сопряженное позволяет избавиться в этом выражении от радикалов:
сопряженным, а его умножение на сопряженное позволяет избавиться в этом выражении от радикалов:
(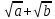 )
) (
(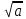 -
-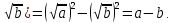
Таким образом, домножая числитель и знаменатель дроби на выражение, сопряженное числителю, получим:
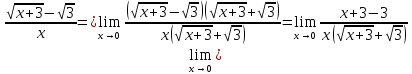 =
=
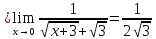 .
.
Ответ: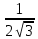 .
.
Важное место в теории пределов занимают первый и второй замечательные пределы.
Первый замечательный предел имеет вид:
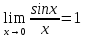 .
.
Задача 1.4. Найти предел: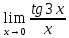
.
Решение .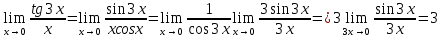 .
.
Ответ: 3.
Второй замечательный предел представляет собой неопределенность вида и записывается одним из нижеследующих способов:
и записывается одним из нижеследующих способов:
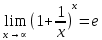 или
или 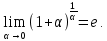
Задача 1.5. Найти функции: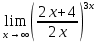 .
.
Решение: Убедимся сначала, что данное выражение представляет собой неопределенность вида . Далее вычислим указанный предел, приводя его ко второму замечательному пределу, записанному в виде:
. Далее вычислим указанный предел, приводя его ко второму замечательному пределу, записанному в виде:
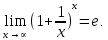
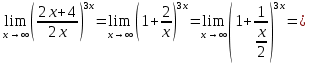
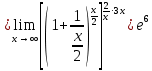 .
.
Ответ: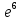 .
.
Раздел 2. Производная функции и ее приложения
Пусть функция определена в некоторой точке
определена в некоторой точке  и в окрестности этой точки, а
и в окрестности этой точки, а 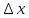 – приращение аргумента, такое, что
– приращение аргумента, такое, что 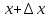 принадлежит указанной окрестности. Тогда
принадлежит указанной окрестности. Тогда 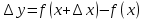 называется приращением данной функции. Если существует
называется приращением данной функции. Если существует
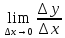 ,
,
то этот предел называется производной функции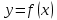 в точке
в точке  и обозначается
и обозначается 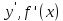 или
или 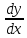 , а функция называется дифференцируемой в точке
, а функция называется дифференцируемой в точке  .
.
Функция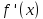 , определенная во всех точках, в которых существует указанный предел, называется производной функции
, определенная во всех точках, в которых существует указанный предел, называется производной функции 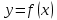 .
.
Рассмотрим технику вычисления производных или, другими словами, технику дифференцирования.
Таблица производных элементарных функций:
1.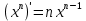 9.
9. 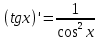
1*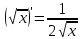 10.
10. 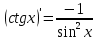
1**.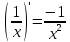 11.
11. 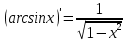
2.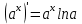
4. Контрольная работа выполняется самостоятельно.
5. В конце работы указывается использованная литература.
6. Контрольная работа подписывается с указанием даты выполнения.
7. Контрольные работы, выполненные без соблюдения изложенных выше правил или по чужому варианту, не зачитываются и возвращаются.
5. Сдача экзаменов
К сдаче экзаменов допускаются студенты, имеющие выполненную и зачтенную контрольную работу. Экзамен сдается устно.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО РАЗДЕЛАМ КУРСА
Внимание!
Данные методические указания предназначены для краткого ознакомления с дисциплиной «Высшая математика». В них приведены теоретические результаты без доказательства и рассмотрены примеры решения задач, подобных задачам, содержащихся в контрольной работе. При изучения дисциплины «Высшая математика» кроме данного пособия необходимо использовать для самостоятельной работы литературу из списка, приведенного на стр. 5-6.
Раздел 1 Теория пределов, непрерывность функций
Не касаясь строгого определения предела, приведем здесь лишь смысл этого понятия.
Пусть задана некоторая функция
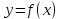 , определенная в окрестности точки
, определенная в окрестности точки 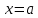 , кроме, быть может, самой точки. Пределом функции
, кроме, быть может, самой точки. Пределом функции 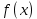 при
при 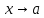 называется число
называется число 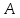 , к которому стремится функция, при приближении аргумента
, к которому стремится функция, при приближении аргумента 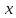 к числу
к числу 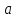 :
:.
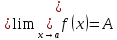
.
При вычислении предела первое, что надо сделать – подставить
 в выражение функции. Если указанное значение аргумента функции принадлежит области ее определения, то в результате получится некое число
в выражение функции. Если указанное значение аргумента функции принадлежит области ее определения, то в результате получится некое число 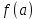 , которое и является пределом функции при
, которое и является пределом функции при  .
. Однако, в некоторых случаях при подстановке
 в формулу появляется так называемая неопределенность, которая символически записывается в одном из следующих видов:
в формулу появляется так называемая неопределенность, которая символически записывается в одном из следующих видов: 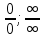 или
или 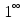 . В этом случае необходимо применять специальные методы вычисления пределов, называемые методами раскрытия неопределенностей. Также необходимо рассмотреть методы вычисления пределов функций при
. В этом случае необходимо применять специальные методы вычисления пределов, называемые методами раскрытия неопределенностей. Также необходимо рассмотреть методы вычисления пределов функций при 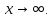
Задача 1.1. Найти предел:
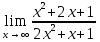
Решение. Убеждаемся, что при
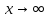 числитель и знаменатель выражения стремятся к бесконечности, и получаем неопределенность вида
числитель и знаменатель выражения стремятся к бесконечности, и получаем неопределенность вида 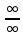 . Делим числитель и знаменатель рациональной дроби на переменную в наивысшей степени, то есть, в данном случае, на
. Делим числитель и знаменатель рациональной дроби на переменную в наивысшей степени, то есть, в данном случае, на 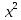 . Учитывая, что
. Учитывая, что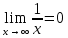 и
и 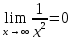 , а также используя ряд свойств пределов, получаем:
, а также используя ряд свойств пределов, получаем: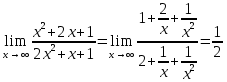 .
.Задача 1.2. Найти предел:

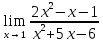
Решение. В первую очередь подставим в выражение функции
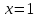 и убедимся, что данном случае мы имеем дело с неопределенностью вида
и убедимся, что данном случае мы имеем дело с неопределенностью вида 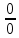 . Далее используем метод разложения трехчлена на множители, а именно:
. Далее используем метод разложения трехчлена на множители, а именно: 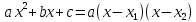
, где
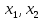 - корни квадратного трехчлена. Учитывая, что корни знаменателя
- корни квадратного трехчлена. Учитывая, что корни знаменателя 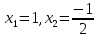 , а корни знаменателя
, а корни знаменателя 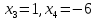 , представим исходный предел в виде:
, представим исходный предел в виде: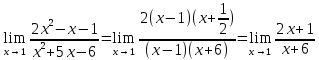 .
.Заметим, что вместе с сокращением в числителе и знаменателе множителя
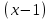 , из выражения уходит неопределенность. Теперь в выражение под знаком предела можно подставить
, из выражения уходит неопределенность. Теперь в выражение под знаком предела можно подставить  и получить, что данный предел равен
и получить, что данный предел равен 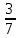 .
.Ответ:
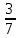 .
.Задача 1.3. Найти предел:
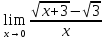 .
.Решение. Подставляем данное выражение
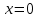 и получаем неопределенность вида
и получаем неопределенность вида 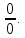
Выражения
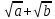 называется для выражения
называется для выражения 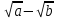 сопряженным, а его умножение на сопряженное позволяет избавиться в этом выражении от радикалов:
сопряженным, а его умножение на сопряженное позволяет избавиться в этом выражении от радикалов: (
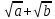 )
) (
(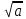 -
-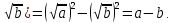
Таким образом, домножая числитель и знаменатель дроби на выражение, сопряженное числителю, получим:
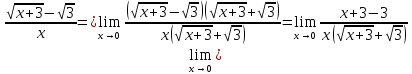 =
=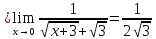 .
.Ответ:
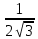 .
.Важное место в теории пределов занимают первый и второй замечательные пределы.
Первый замечательный предел имеет вид:
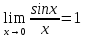 .
.Задача 1.4. Найти предел:
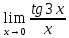
.
Решение .
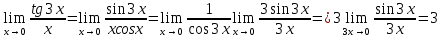 .
.Ответ: 3.
Второй замечательный предел представляет собой неопределенность вида
 и записывается одним из нижеследующих способов:
и записывается одним из нижеследующих способов: 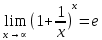 или
или 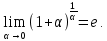
Задача 1.5. Найти функции:
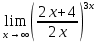 .
.Решение: Убедимся сначала, что данное выражение представляет собой неопределенность вида
 . Далее вычислим указанный предел, приводя его ко второму замечательному пределу, записанному в виде:
. Далее вычислим указанный предел, приводя его ко второму замечательному пределу, записанному в виде: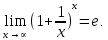
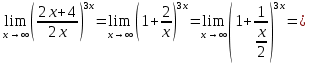
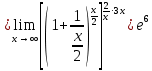 .
.Ответ:
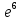 .
.Раздел 2. Производная функции и ее приложения
Пусть функция
 определена в некоторой точке
определена в некоторой точке  и в окрестности этой точки, а
и в окрестности этой точки, а 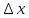 – приращение аргумента, такое, что
– приращение аргумента, такое, что 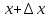 принадлежит указанной окрестности. Тогда
принадлежит указанной окрестности. Тогда 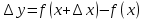 называется приращением данной функции. Если существует
называется приращением данной функции. Если существует 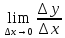 ,
,то этот предел называется производной функции
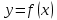 в точке
в точке  и обозначается
и обозначается 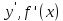 или
или 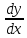 , а функция называется дифференцируемой в точке
, а функция называется дифференцируемой в точке  .
.Функция
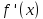 , определенная во всех точках, в которых существует указанный предел, называется производной функции
, определенная во всех точках, в которых существует указанный предел, называется производной функции 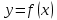 .
.Рассмотрим технику вычисления производных или, другими словами, технику дифференцирования.
Таблица производных элементарных функций:
1.
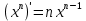 9.
9. 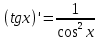
1*
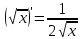 10.
10. 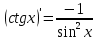
1**.
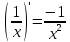 11.
11. 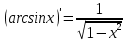
2.