Файл: Учебнометодическое пособие по курсу высшая математика часть 1 для студентов Центра заочного образования по программе.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 223
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
единицей в множестве действительных чисел, то есть для любой матрицы  выполняется соотношение:
выполняется соотношение:
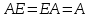 .
.
Квадратная матрица, имеющая определитель , отличный от нуля
, отличный от нуля 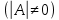 , называется невырожденной матрицей. Любая невырожденная матрица имеет обратную матрицу
, называется невырожденной матрицей. Любая невырожденная матрица имеет обратную матрицу 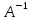 :
:
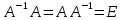 .
.
Метод определения обратной матрицы приведен в следующем примере:
Задача 5.3. Найти обратную матрицу для матрицы
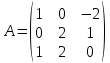 .
.
Решение. Сначала проверяем матрицу на новорожденность и вычисляем . Определитель этой матрицы вычислен в задаче 5.2: |A|=2
. Определитель этой матрицы вычислен в задаче 5.2: |A|=2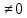 . Отсюда следует, что матрица невырожденная и, поэтому, имеет обратную матрицу. Нахождение обратной матрицы состоит из трех шагов:
. Отсюда следует, что матрица невырожденная и, поэтому, имеет обратную матрицу. Нахождение обратной матрицы состоит из трех шагов:
Шаг 1: Построение матрицы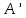 , состоящей из алгебраических дополнение элементов матрицы
, состоящей из алгебраических дополнение элементов матрицы 
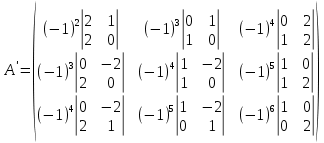 =
=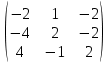 .
.
В этом случае мы каждый элемент исходной матрицы заменяем на его алгебраическое дополнение.
Шаг 2. Производим с матрицей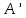 операцию транспонирования, то есть операцию преобразования всех строк матрицы в одноименные столбцы:
операцию транспонирования, то есть операцию преобразования всех строк матрицы в одноименные столбцы:
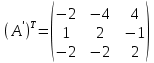 .
.
Шаг 3. Умножаем полученную матрицу на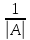 , в нашем случае на
, в нашем случае на 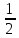 :
:
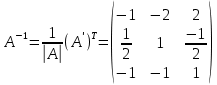 .
.
В случае нахождения обратной матрицы рекомендуется сделать проверку и убедиться, что полученная матрица является обратной к заданной.
Система из трех линейных уравнений с тремя неизвестными может быть записана матричным способом. Введем следующие матрицы:
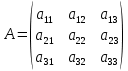 ;
; 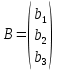 ;
; 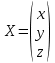 ,
,
где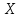 - матрица системы, B – матрица-столбец свободных членов и
- матрица системы, B – матрица-столбец свободных членов и 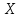 - матрица неизвестных. Тогда систему можно представит в виде:
- матрица неизвестных. Тогда систему можно представит в виде:
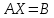 .
.
Умножая правую и левую части последнего соотношения на , слева, получим:
, слева, получим:
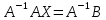 ,
,
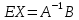 ,
,
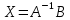 .
.
Задача 5.4. Найти решение системы линейных уравнений, заданной в задаче 5.1, матричным способом.
Решение.
Для матрицы системы в задаче 5.1 найдена обратная матрица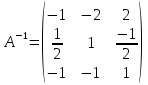 . Учитывая, что матрица свободных членов данной системы
. Учитывая, что матрица свободных членов данной системы 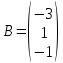 , получим решение системы в виде:
, получим решение системы в виде:
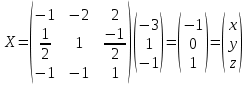 .
.
Ответ: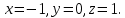
Контрольная работа №1
1. Вычислить указанные пределы, не пользуясь правилом Лопиталя.
2. Вычислить производные указанных функций.
3. Вычислить неопределенные интегралы.
4. Вычислить определенный интеграл
5. Решить систему линейных уравнений по правилу Крамера и матричным методом.
Вариант 00
Вариант 01
Вариант 02
Вариант 03
Вариант 04
Вариант 05
 выполняется соотношение:
выполняется соотношение: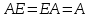 .
.Квадратная матрица, имеющая определитель
 , отличный от нуля
, отличный от нуля 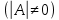 , называется невырожденной матрицей. Любая невырожденная матрица имеет обратную матрицу
, называется невырожденной матрицей. Любая невырожденная матрица имеет обратную матрицу 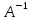 :
: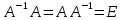 .
.Метод определения обратной матрицы приведен в следующем примере:
Задача 5.3. Найти обратную матрицу для матрицы
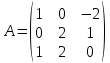 .
.Решение. Сначала проверяем матрицу на новорожденность и вычисляем
 . Определитель этой матрицы вычислен в задаче 5.2: |A|=2
. Определитель этой матрицы вычислен в задаче 5.2: |A|=2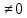 . Отсюда следует, что матрица невырожденная и, поэтому, имеет обратную матрицу. Нахождение обратной матрицы состоит из трех шагов:
. Отсюда следует, что матрица невырожденная и, поэтому, имеет обратную матрицу. Нахождение обратной матрицы состоит из трех шагов:Шаг 1: Построение матрицы
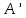 , состоящей из алгебраических дополнение элементов матрицы
, состоящей из алгебраических дополнение элементов матрицы 
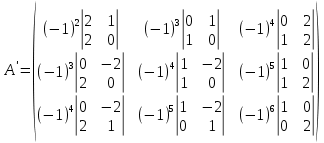 =
=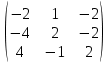 .
.В этом случае мы каждый элемент исходной матрицы заменяем на его алгебраическое дополнение.
Шаг 2. Производим с матрицей
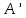 операцию транспонирования, то есть операцию преобразования всех строк матрицы в одноименные столбцы:
операцию транспонирования, то есть операцию преобразования всех строк матрицы в одноименные столбцы: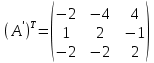 .
.Шаг 3. Умножаем полученную матрицу на
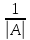 , в нашем случае на
, в нашем случае на 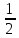 :
: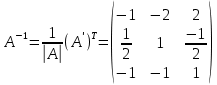 .
.В случае нахождения обратной матрицы рекомендуется сделать проверку и убедиться, что полученная матрица является обратной к заданной.
Система из трех линейных уравнений с тремя неизвестными может быть записана матричным способом. Введем следующие матрицы:
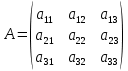 ;
; 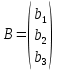 ;
; 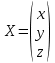 ,
,где
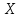 - матрица системы, B – матрица-столбец свободных членов и
- матрица системы, B – матрица-столбец свободных членов и 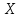 - матрица неизвестных. Тогда систему можно представит в виде:
- матрица неизвестных. Тогда систему можно представит в виде: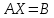 .
.Умножая правую и левую части последнего соотношения на
 , слева, получим:
, слева, получим: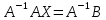 ,
, 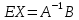 ,
, 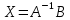 .
. Задача 5.4. Найти решение системы линейных уравнений, заданной в задаче 5.1, матричным способом.
Решение.
Для матрицы системы в задаче 5.1 найдена обратная матрица
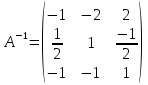 . Учитывая, что матрица свободных членов данной системы
. Учитывая, что матрица свободных членов данной системы 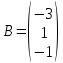 , получим решение системы в виде:
, получим решение системы в виде: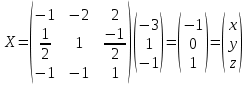 .
.Ответ:
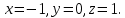
Контрольная работа №1
1. Вычислить указанные пределы, не пользуясь правилом Лопиталя.
2. Вычислить производные указанных функций.
3. Вычислить неопределенные интегралы.
4. Вычислить определенный интеграл
5. Решить систему линейных уравнений по правилу Крамера и матричным методом.
Вариант 00
| 1а | 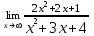 | 1б | 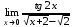 | 1в | 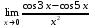 | 1г | 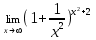 |
| 2а | 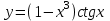 | 2б | 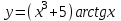 | 2в | 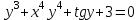 | 2г | 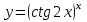 |
| 3а | 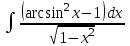 | 3б | 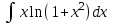 | 4 | 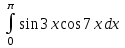 | 5 | -2y +3z = -8 3x +y +3z = 1 -x +y +z = -3 |
Вариант 01
| 1а | 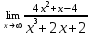 | 1б | 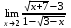 | 1в | 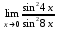 | 1г | 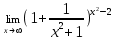 |
| 2а | 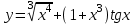 | 2б | 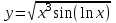 | 2в | 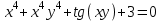 | 2г | 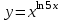 |
| 3а | 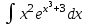 | 3б | 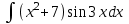 | 4 | 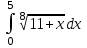 | 5 | -5x +4y -3z = 6 -6x - 2y +5z = 9 4x - y - 3z = -8 |
Вариант 02
| 1а | 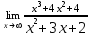 | 1б | 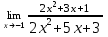 | 1в |  | 1г | 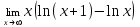 |
| 2а | 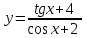 | 2б | 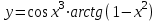 | 2в | 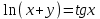 | 2г | 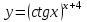 |
| 3а | 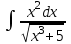 | 3б | 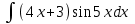 | 4 | 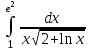 | 5 | -y - 5z = 2 -5x +y +2z = - 4 -5x +5y +4z = 6 |
Вариант 03
| 1а | 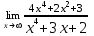 | 1б | 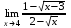 | 1в | 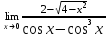 | 1г | 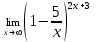 |
| 2а | 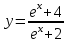 | 2б | 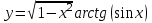 | 2в | 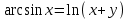 | 2г | 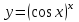 |
| 3а | 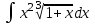 | 3б | 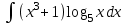 | 4 | 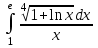 | 5 | -4x -6y -z = -1 -x -2y -5z = 5 -x +2z = -4 |
Вариант 04
| 1а | 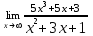 | 1б | 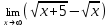 | 1в |  | 1г | 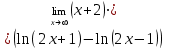 |
| 2а | 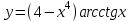 | 2б | 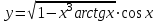 | 2в | 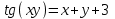 | 2г | 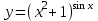 |
| 3а | 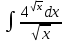 | 3б | 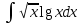 | 4 | 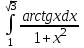 | 5 | x +4y +z = 7 -3x +2y +z = -1 5x -2y -2z = 5 |
Вариант 05
| 1а | 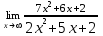 | 1б | 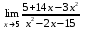 | 1в |  | 1г | 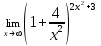 |
| 2а | 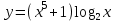 | 2б | 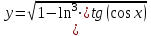 | 2в | 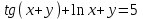 | 2г | 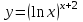 |
| 3а | 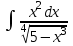 | 3б | 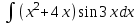 | 4 | 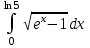 | 5 | -3x + 4y +5z = -4 -5x +5y +5z = -5 2y - z = 3 |