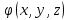Файл: Дрі Химиялы жне фармацевтикалы технологияны негізгі процестерін жіктеу. Химиялы ндірісті отайландыру.docx

3.14-сурет. Координата жүйесіндегі жергілікті жылдамдық.
Бұлардың функционалды жылдамдығын былай жазамыз:







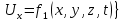
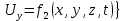
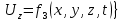
Осы функциялардың нақтылы жағдайдағы ағын шамасын білсек, онда кез келген уақыттағы сұйық ағынның бөлініп таралуын білуге болады. Лагранж әдісін пайдалансақ онда,белгіленген нүктенің сұйықпен бірге жылжу кезіндегі координатасын x, y, z белгілеп, оның кинематикасын зерттейміз. Ол үшін, ағын ішіндегі нүктені қимылсыз координата жүйесімен белгілеп, олардың координатасын 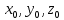деп, уақыт кезеңінен . Сонда, сұйық ішіндегі белгіленіп алынған нүктенің траекториядағы қимыл – қозғалысы бір–бірінен айырмашылығы бастапқы координаталарының тұрған шамасына байланысты. Әрбір қаралып отырған нүктенің координатасы үшін олардың функционалды тәуелділігі бар: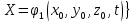







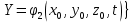
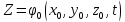
Осы нүктелердің жылжу жылдамдығы ағынның жергілікті жылдамдығымен сәйкес келеді:







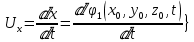
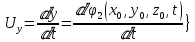
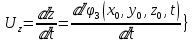
Лагранж әдісі бойынша сұйықтың және нүктелердің t уақыт ішіндегі кеңістіктегі өз траекториясымен ағып өтуін сипаттайды да, сұйықтағы нүктенің осыдан t уақыт бұрын қай жерде болғанын және t уақыттан кейін қай жерде болатынын да анықтауға болады. Сұйық ішіндегі барлық нүктелердің траекторияларын анықтайтын теңдеулерді жазу өте қиын болғандықтан, Лагранж әдісін гидродинамикада тіптен пайдаланбайды.

Көбінесе, Эйлер әдісін қолданады. Сұйық қозғалысының түрлерін қарастырамыз, олар сұйық ағынының қалыптасқан (тұрақты) және қалыптаспаған (тұрақсыз) болып бөлінеді.

Қалыптасқан қозғалыс деп ағынның қай нүктесіндегі болсын, сұйықтың тереңдігі, жылдамдығы және қысым уақыт аралығындағы өзгермеуін айтады, яғни

---

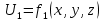
және 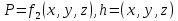уақытқа байланысты болмайды.

Мысалы, тұрақты қозғалысқа бензин багінен аққан жанармайды жатқызуға болады, егер оның деңгейі өзгермей аққан кездегі күйі, сонымен қатар тоғандағы су қозғалысы, сондықтан оның геометриялық көрсеткіштері көлденең қимасы мен тереңдігі тұрақты болуы керек.

Қалыптаспаған сұйық ағыны деп ағынның кеңістіктегі қай нүктесінде болсадағы сұйықтың жылдамдығы мен қысым уақыт аралығында өзгеріп отыратын қозғалысын айтады.

Кейбір, жалпы жағдайда қалыптасқан ағынның тереңдігі қысым және жылдамдығының координатасы уақытына байланысты болады.

Қалыптаспаған қозғалыста ағыс сызығы уақыт ішінде өзгеріп отырады. Ағынның барлық нүктелерінде бір сәтте жүргізілген жылдамдық векторлары орталық сызыққа жанама болып бағытталуын қисық сызықты ағыс сызығы деп атайды (3.15-сурет).



3.15-сурет. Ағын нүктелерінде бір сәтте жүргізілген жанама вектор жылдамдығы.

Егер ағын қозғалысы белгіленген нүктелердегі ағынның жылдамдығы бағыты уақыт аралығында өзгереді.

Ағыс ішіндегі нүктенің x, y, z координатасының құраушы жергілікті жылдамдығы координата осінің бойымен болады. Ағыс сызығы бойымен ауысқандағы арақашықтығын ds деп, нүктелерінің координатасын x+dx, y+dy және z+dz болса: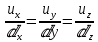



бұл теңдеу ағыс сызығының теңдеуідеп аталады.

Қозғалыстағы сұйық ағыны тұйық контур жүргізін, ондағы шексіз элементарлы кішкене алаңшаның жазықтықпен шектелген жеріндегі нүктелеріне ток сызығын жүргізсек, түтікті көрінбейтін жазықтық ток түтігі деп атайды.

Ток түтігі мен шектелген сұйық бөлшектерінің массасын элементарлы сұйық ағыншасы деп атайды. Барлық элементарлы сұйық ағыншаларының әр түрлі жылдамдықта болып ағуын сұйық тасқыны (ағыны) дейді.

Сұйық ағыншасы үшке бөлінеді:

а) еркін ағыс деп үш жағынан ағын арнасына тірелген, ашық бетті су қозғалысын айтады. Мұндағы ағын тек салмақ күштерінің жанама (τ) әсерінен қозғалады;

ә) тегеурінді ағын деп жан-жағынан арнаға тірелген ағысты қысымды айтады. Ағынның қозғалысы қысым күшінің әсерінен болады (құбырдағы ағын);

---

б) арнасыз ағын деп жан-жағы газбен немесе сұйықпен қоршалған ортада ағуын айтады. Кейде оны гидравликалыұ ағынша деп те атайды.

Сұйық тасқынының гидравликалық элементтері:

Сұйық шығыны және орташа жылдамдығы.

Сұйық қозғалысының гидравликалық көрсеткіштеріне траектория туралы ұғымнан басқа ток сызықтары, элементарлы ағыншалар, тасқын, ағынның көлденең қимасы, тоғанның ылғалданған периметрі, гидравликалық радиус, сұйықтың шығыны мен орташа жылдамдығы жатады.

Көлденең қимасы (ω) деп ағын бағыты мен барлығ ток сызықтарында перпендикуляры көлденең қима ауданын айтады. Мысалы, дөңгелек құбырдың диаметрі d суға толы барлық қимасының дөңгелек ауданында тең болады, яғни



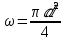
Ағын қимасының ауданы мен жылдамдығының көбейтіндісін сұйықтың немесе газдың элементарлы шығыны деп атайды.



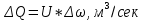
мұндағы, U -сұйықтың жергілікті жылдамдығы, м 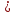с; 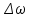– элементарлы көлем.

Белгілі уақыт ішінде сұйық қимасынан ағып өтетін сұйық массасын:



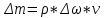
формуласымен есептейді.

Ал қима ауданы ω ағыншалардың қимасының жиынтығына тең болады:



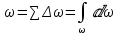
Сұйықтың шығыны ( 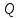) деп барлық элементарлы ағыншалардың жиынтығын айтады: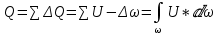



Сұйықтың массалық шығыны(m) – олардың әрбір элеменарлы ағыншалардың массалық шығынының жиынтығына тең болады:



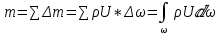
Ылғалданған периметр ( 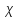) – сұйықтың көлденең қимасының периметрінің қатты қабырғамен жұғысқан жері. Мысалы, дөңгелек құбырдың толық қимасымен сұйықтың аққан кездегі ылғалданған периметрі құбырдың шеңберінің ұзындығына тең, яғни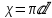

---

.

Гидравликалық радиус (R) -құбырдың көлденең қимасының ауданының, ылғалданған периметрінің қатынасына тең:



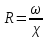
Мысалы, құбырдағы сұйықтың толық қимасымен аққандағы гидравликалық радиус, оның диаметрінің төрттен біріне тең:



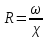
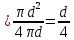
Сұйық ағынның ортша жылдамдығы сұйық шығыны қима ауданының қатынасына тең болады:

,

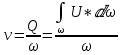бұдан

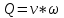
Сұйықтың үздіксіздік-дифференциалды теңдеуі:

Үздіксіз ағындар деп ағысы үзілмей, арна кеңістігін толық толтырып ағатын ағындарды айтады. Бұл жағдайда козғалыстағы сығылмайтын сұйық шамасының сандық (не үлкейтіп, не кішірейтпейді) уақыт аралығында өзгермейді. Элементарлы параллелепипедтің қырынан (жанына) ағып өтетін сұйық массасын қарастырамыз. (3.16-сурет).



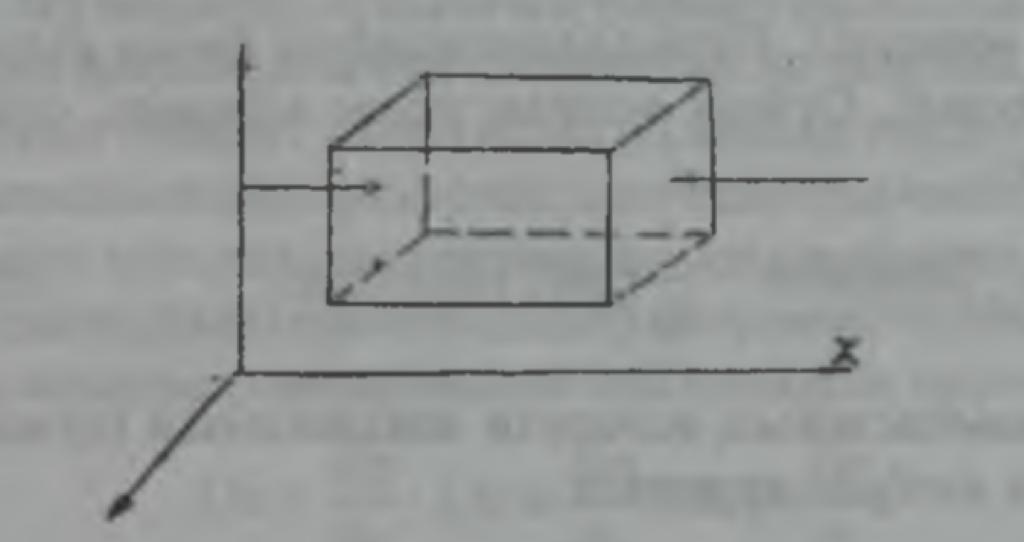
3.16-сурет. Сұйықтың үздіксіздік-дифференциалды теңдеуін дәлелдеу.
Параллелепипедтің сол жақ қырынан ағып кіретін сұйықтың жылдамдығын 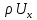, ал оң жақ қырынан ағып шығатын жылдамдығын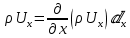



деп белгілейді.

Ағын ішінен x, y, z координатты нүктені таңдап алып, O’ нүктесіндегі сұйық ағынның жылдамдығын құраушы 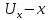осі бойымен, 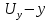осі бойымен және 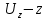осі бойымен өтеді. Параллелепипедтің 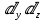элементарлы ауданшасының O₁ нүктесіндегі уақыт аралығын (dt) белгілейді. Сонымен параллелепипедтің ішіне 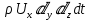сұйық массасы ағып кіреді. Параллелепипедтің сол жақ қырынан O’ нүктесінен dt уақыт аралығында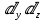

---

көлемінен O” нүктесіне жетеді де 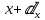координатасында болады, ал ағып шыққан сұйық массасының көлемін былай табады: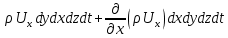



Демек, сұйық аққан кезде құраушы жылдамдығы 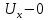нүктесіндегі параллелепипедтің сұйық массасы 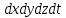, ал оның ауданы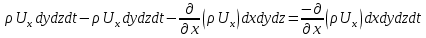



шамасына өзгереді. Параллелепипедтің басқа қырынан 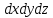көлемді. Сұйық осыған ұқсас өзгереді, оны былай табады: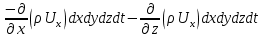



Сұйық массасының өзгеруін жиынтығын (суммасы) белгіленген 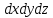ауданын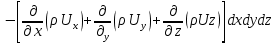



арқылы табады.

Сұйық ауданының тығыздығы 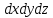ауданымен шектелген 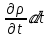өзгеруі мүмкін, ол оның масса осы ауданда 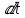уақыт аралығында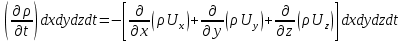



болады.

шамасы теңдеудің екі жағында да бар, оны есептемесек, белгілі нүктедегі ағынның тоқтаусыз ағу шарты бойынша: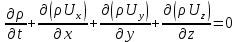



болады.

Бұл теңдеуді гидромеханикада сұйықтың үздіксіз ағу теңдеуі деп атайды.

Егер ағын қалыптасқан қозғалыс түрінде болса 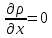онда теңдеу (1.70), былай жазылады: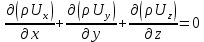



Егер сұйық сығылмайтын болса, яғни 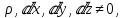онда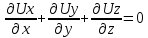



(3.70) теңдеуді сұйықтың үзілмеушілігінің дифференциалды формадағы сығылмайтын, өз бетімен аққан суға арналған тендеуі деп атайды (JI.Эйлер теңдеуі).

Сығылмайтын сұйықтың потенциалды қозғалысы үшін, функция

---