Файл: Методические рекомендации для обучающихся к выполнению практических работ по учебной дисциплине.docx
Добавлен: 12.01.2024
Просмотров: 185
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| 4. Вычислить площадь плоской фигуры с помощью формулы Ньютона – Лейбница. | ||
| 4 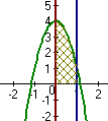 .1.1 .1.1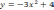 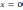 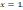 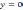 | 4 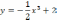 .1.2 .1.2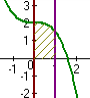 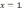   | 4 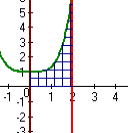 .1.3 .1.3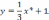 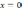 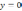 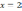 |
Критерии оценки:
«5» - ставится за 6 верно выполненных заданий;
«4» - ставится за 5-4 верно сделанных задания;
«3» - ставится за 3 верно выполненных задания;
«2» - если решено менее 3 заданий.
Литература.
Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014.
Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014.
Тема 6.3 Интеграл и его применение.
Практическая работа № 32
Вычисление площадей криволинейных трапеций.
Цель: закрепление знаний, отработка навыков вычисления площади криволинейной трапеции.
Пояснения к работе:
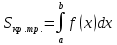
(1)
План выполнения работы.
1. Постройте фигуру по заданным условиям.
2. Составьте интеграл по формуле (1)
3. Вычислите интеграл.
Пример: Найдите площадь фигуры, ограниченной линиями: у = -
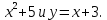
Решение: Найдём абсциссы точек пересечения параболы у = -
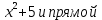
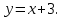 Для этого решим систему:
Для этого решим систему: 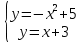 , откуда
, откуда 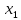 = - 2,
= - 2, 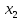 = 1.
= 1. Найдём площадь
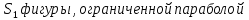 у = -
у = -  = 12 (кв.ед.). Найдём площадь
= 12 (кв.ед.). Найдём площадь 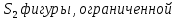 прямыми
прямыми 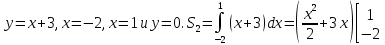 = 7,5 (кв.ед.). Площадь искомой фигуры есть S =
= 7,5 (кв.ед.). Площадь искомой фигуры есть S = 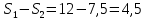 (кв.ед.).
(кв.ед.).Задания к практической работе.
| Вариант 1 | Вариант 2 |
| Найдите площадь фигуры, ограниченной линиями: | |
| 1. у = 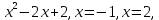 ось ОХ. ось ОХ. | 1. 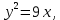 х = 16, х = 25, у = 0. х = 16, х = 25, у = 0. |
| 2. 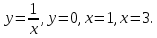 | 2. у=2 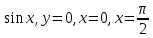 . . |
| 3. х-у-1=0, х=-4, х=-2, у=0. | 3. у = - 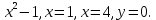 |
| 4. у = 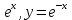 | 4. у = 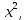 у = у = 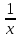 , 1 , 1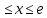 |
| 5. у = 1 + 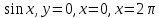 | 5. у = 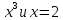 |
Критерии оценки:
«5» ставится за 5 верно решенных заданий;
«4» ставится за 4 верно решенных задания;
«3» ставится за 3 верно решенных задания;
«2» - если решено менее 3 заданий.
Литература.
Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014.
Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014.
Раздел 7 Элементы теории вероятностей и математической статистики
Тема 7.1. Элементы теории вероятностей
Практическая работа № 33
Решение задач на сложение и умножение вероятностей.
Цель: контроль и закрепление знаний, умений, навыков студентов по теме теория вероятности.
| I часть | Факториал | Перестановки | Размещения | Сочетания |
| а) Дать определение | | | | |
| б) Записать формулу | n! = … | 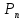 = … = … | 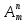 = … = … | 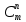 = … = … |
| в) Вычислить | 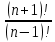 = … = … | 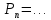 | 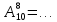 | 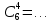 |
II часть
а) Решите уравнение:
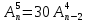 ; б) Решите систему уравнений:
; б) Решите систему уравнений: 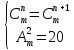
III часть
1. В урне находятся 20 черных и 15 белых шаров. Наудачу вынимается 1 шар, который оказался белым. После этого берут еще один шар. Найдите вероятность того, что этот шар тоже окажется белым.
2. Найдите вероятность того, что наудачу взятое двузначное число окажется кратным либо 4, либо 5, либо тому и другому одновременно.
Критерии оценки
: «5» ставится за все верно решенные задания;
«4» ставится за I и II части вместе; за I и III части вместе;
«3» ставится за II или III часть;
«2» – в остальных случаях.
Литература:
Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014.
Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014.
Раздел 8 УРАВНЕНИЯ И НЕРАВЕНСТВА.
Тема 8.1Уравнения и системы уравнений. Неравенства и системы неравенств с двумя переменными.
Практическая работа № 34
Основные приемы решения уравнений и неравенств. Способ введения новых переменных.
Цель: закрепление знаний, отработка навыков решения уравнений.
Пояснения к работе: Общие приёмы решения уравнений:
1. Разложение на множители. Пример.
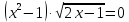
Решение.
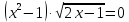 ОДЗ: 2х-1
ОДЗ: 2х-1 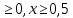
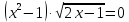 ;
; 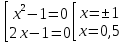 х = - 1 - не входит в ОДЗ. Ответ: 0,5; 1
х = - 1 - не входит в ОДЗ. Ответ: 0,5; 12. Замена переменной. Пример.
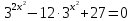
Решение. Пусть
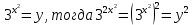 . Подставив в исходное уравнение, получаем:
. Подставив в исходное уравнение, получаем: 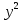 - 12 у + 27 = 0
- 12 у + 27 = 0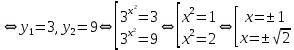 3. Использование свойств функций.
3. Использование свойств функций.Пример. Решите уравнение:
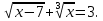
Решение. ОДЗ: х - 7
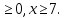
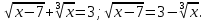 Если
Если 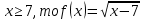 - возрастает, а g
- возрастает, а g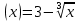 - убывает, следовательно, уравнение
- убывает, следовательно, уравнение 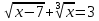 имеет единственный корень, х = 8. ответ: 8.
имеет единственный корень, х = 8. ответ: 8.Задания к практической работе.
| Вариант 1 | Вариант 2 |
| Решите 1. 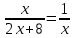 2. 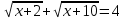 3. 9 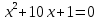 4. 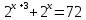 5. 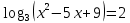 6. 2 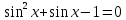 7. 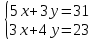 8. 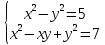 | уравнения: 1. 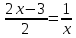 2. 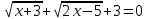 3. 5 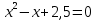 4. 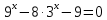 5. 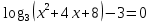 6. 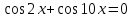 7. 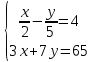 8. 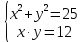 |
Критерии оценки:
«5» - ставится за 7-8 верно выполненных заданий;
«4» - ставится за 5-6 верно выполненных задания;
«3» - за 3-4 верно выполненных задания;
«2» - менее трёх заданий.
Литература.
Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014.
Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014.
Тема 8.1Уравнения и системы уравнений Неравенства и системы неравенств с двумя переменными.
Практическая работа № 35
Решение иррациональных уравнений.
Иррациональные уравнения.
Цель: закрепление знаний, отработка навыков решения иррациональных уравнений.
Пояснения к работе: Определение. Иррациональным называется уравнение, содержащее переменную под знаком корня.
Методы решения: 1) возведение в степень обеих частей уравнения;
2) введение новой переменной (замена переменной).
Замечание: при возведении обеих частей уравнения в четную степень возможно появление посторонних корней. В этом случае обязательна проверка найденных корней подстановкой в исходное уравнение.
Пример. Решить уравнение:
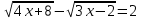 .
. Решение: Возводим обе части уравнения в квадрат.
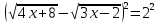 ;
;4х + 8 -2
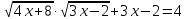 ; 7х + 2 = 2
; 7х + 2 = 2 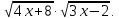
Возводим еще раз в квадрат:
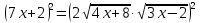 ;
;49
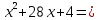 4
4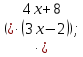
49
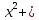 28х +4 = 4
28х +4 = 4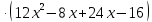 ;
;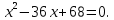
Найдя корни квадратного уравнения получим:
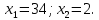
Проверка:
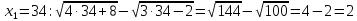 .
. 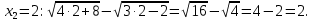 Ответ:
Ответ: 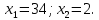
Задания к практической работе.
| Вариант 1 | Вариант 2 |
| 1. 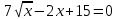 | 1.: 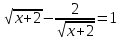 |
| 2. 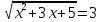 | 2. 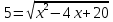 |
| 3. 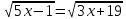 | 3. 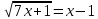 |
| 4. 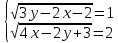 | 4. 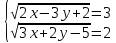 |