Файл: Методические рекомендации для обучающихся к выполнению практических работ по учебной дисциплине.docx
Добавлен: 12.01.2024
Просмотров: 199
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Ответ: 1.
Задания к практической работе.
Критерии оценки:
«5» - ставится за 5 верно выполненных заданий;
«4» - ставится за 4 верно сделанных задания;
«3» - ставится за 3 верно выполненных задания;
«2» - если решено менее 3 заданий.
Тема 6.2. Производная и её применение.
Практическая работа № 27
Производная. Понятие о производной функции, ее геометрический и физический смысл.
Цель: закрепление знаний, отработка навыков вычисления производных.
Пояснения к работе.
Производная функции у = f(х), в точке х0, выражает скорость изменения функции в этой точке.
2. Если функция задана законом прямолинейного движения S = S(t), то S' (t) –?
Скорость движения в момент времени t - это производная по перемещению S' (t) = v(t)
Скорость изменения скорости этого движения, т.е. ускорение а(t) = v' (t) = S' ' (t).
С физической точки зрения дифференцирование – определение скорости изменения переменной величины. Производная, таким образом, играет роль скорости изменения зависимой переменной y по отношению к изменению независимой переменной х.
Выясняем формулы из физики, где используется производная.
Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности.
Таблица производных
Задания к практической работе.
Найдите производную функции.
Найти необходимые величины.
Критерии оценки:
«5» ставится за 8-10 верно решенных заданий;
«4» ставится за 7-6 верно решенных задания;
«3» ставится за 5 верно решенных задания;
«2» - если решено менее 5 заданий.
Тема 6.2. Производная и её применение.
Ответ: 1.
Задания к практической работе.
| № | Вариант 1 | Вариант 2 |
| 1. |  | 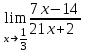 |
| 2. | 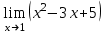 | 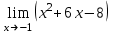 |
| 3. | 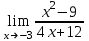 | 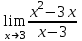 |
| 4. | 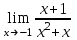 | 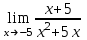 |
| 5. | Вычислите предел при х 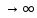 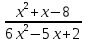 | Вычислите предел при х 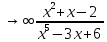 |
Критерии оценки:
«5» - ставится за 5 верно выполненных заданий;
«4» - ставится за 4 верно сделанных задания;
«3» - ставится за 3 верно выполненных задания;
«2» - если решено менее 3 заданий.
Тема 6.2. Производная и её применение.
Практическая работа № 27
Производная. Понятие о производной функции, ее геометрический и физический смысл.
Цель: закрепление знаний, отработка навыков вычисления производных.
Пояснения к работе.
-
Определение. Производной функции у = f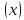 в точке х называется предел отношения приращения функции
в точке х называется предел отношения приращения функции 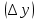 в этой точке к приращению аргумента
в этой точке к приращению аргумента 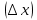 , когда
, когда 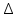 х стремится к 0. Обозначение: f
х стремится к 0. Обозначение: f =
=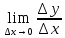
Производная функции у = f(х), в точке х0, выражает скорость изменения функции в этой точке.
2. Если функция задана законом прямолинейного движения S = S(t), то S' (t) –?
Скорость движения в момент времени t - это производная по перемещению S' (t) = v(t)
-
Что есть вторая производная от закона движения?
Скорость изменения скорости этого движения, т.е. ускорение а(t) = v' (t) = S' ' (t).
С физической точки зрения дифференцирование – определение скорости изменения переменной величины. Производная, таким образом, играет роль скорости изменения зависимой переменной y по отношению к изменению независимой переменной х.
Выясняем формулы из физики, где используется производная.
-
υ(t) = х'(t) – скорость. -
a(t) = υ'(t) – ускорение. -
I(t) = q'(t) – сила тока. -
с(t) = Q'(t) – теплоемкость. -
d(l) = m'(l) – линейная плотность. -
K(t) = l'(t) – коэффициент линейного расширения. -
ω(t) = φ'(t) – угловая скорость. -
e(t) = ω'(t) – угловое ускорение.
Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности.
-
N(t) = A'(t) – мощность. -
F(x)= A'(x) – Сила есть производная работы по перемещению. -
Е = Ф'(t) – ЭДС индукции F = р'(t) – 2 закон Ньютона.
| Примеры применения производной в физике | |
| Задача | Решение |
| Тело массой 4 кг движется прямолинейно по закону x(t)=t2+t+1.
3 сек. после начала движения тела?
|
x ' (t) = v (t) = 2t+1, v (3) = 7, a(t)= v' (t) = 2, Wк = (4·72)/2=98 2. F = ma, a(t) = v' (t) = x' ' (t), x ' (t) = v (t) = 2t+1, a(t)= v' (t) = 2, F = ma = 4·2 = 8 H. |
| Угол поворота тела вокруг оси изменяется по закону φ(t)=0,1t2-0,5t+0,2. Найти угловую скорость вращения тела в момент времени t=20с. | ω(t) = φ'(t) φ'(t) = 0,2t-0,5 ω(t) = 0,2t-0,5 ω(20) = 3,5 |
| Для любой точки С стержня АВ длиной 10 см, масса куска стержня АС определяется по формуле m(l)=3l2+5l. Найти линейную плотность стержня в середине отрезка АВ, в конце отрезка. | d(l) = m'(l) m'(l) = 6l+5 d(l) = 6l+5 d(5) = 6·5+5=35 – в середине отрезка d(10) = 6·10+5=65 – в конце отрезка |
| Количество электричества, протекающее через проводник, начиная с момента времени t=0, задаётся формулой q=3t2-3t+4. Найти силу тока в конце 6-й секунды. | I(t) = q'(t) q'(t) = 6t-3 I(t) = 6t-3 I(6) = 6·6-3=33 |
Таблица производных
| f 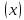 | f 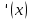 | f 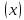 | f 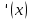 |
| k  f f | k 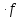 | 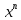 | n 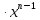 |
| f 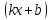 | k 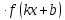 |  |  |
| f + g | f + g |  | -  |
| f 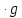 | f 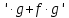 | tg x | 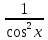 |
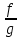 | 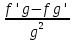 | 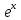 | 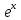 |
| C | 0 | 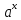 | 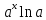 |
| x | 1 | 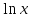 | 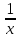 |
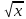 | 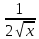 | 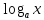 | 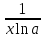 |
Задания к практической работе.
Найдите производную функции.
| Вариант 1 | Вариант 2 | Вариант 3 |
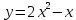 3.1 3.1 | 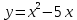 3.6 3.6 | 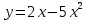 3.11 3.11 |
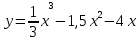 3.2 3.2 | 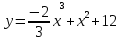 3.7 3.7 | 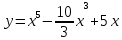 3.12 3.12 |
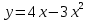 3.3 3.3 | 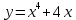 3.8 3.8 | 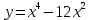 3.13 3.13 |
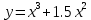 3.4 3.4 | 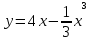 3.9 3.9 | 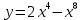 3.14 3.14 |
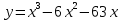 3.5 3.5 | 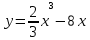 3.10 3.10 | 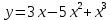 3.15 3.15 |
Найти необходимые величины.
| 1.1 S(t)=2t4+3t2-t+√t3 v(t), a(t)-? | 1.6 S(t)=12t 2-(2/3)t3 v(t), a(t)-? | 1.11 S(t)=21t+2t2-(1/3)t3 v(t), a(t)-? |
| 1.2 S(t)=5sin(3t+1), v(t)-? | 1.7 S(t)=6cos(0,5t-4), v(t)-? | 1.12 S(t)=0,5sin(4t+2), v(t)-? |
| 1.3 x(t)= - 4t2+2t+2, v(1)-? | 1.8 x(t)= √t+2t2 - 3t+2, v(25)-? | 1.13 x(t)=(-1/3)t3+2t2+5t, v(2)-? |
| 1.4 x(t)=t3-4t2, a(5) -? | 1.9 x(t)=0,25t4-2t2, a(1) -? | 1.14 x(t)=t5+3t2-1, a(2) -? |
| 1.5 x(t)=(-1/6)t3 +3t2 – 5, найти t, когда a(t)=0 | 1.10 x(t)=2t3+t-1, найти t, когда a(t)=2 | 1.15 x(t)= (-1/3)t3+2t2+5t, найти t, когда v(t)=0 |
Критерии оценки:
«5» ставится за 8-10 верно решенных заданий;
«4» ставится за 7-6 верно решенных задания;
«3» ставится за 5 верно решенных задания;
«2» - если решено менее 5 заданий.
Тема 6.2. Производная и её применение.