ВУЗ: Нижегородский государственный технический университет
Категория: Решение задач
Дисциплина: Информатика
Добавлен: 13.02.2019
Просмотров: 368
Скачиваний: 3
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Новосибирский государственный технический университет»
Кафедра Автоматизированных систем управления
Отчет по лабораторной работе №3
по дисциплине «Методы анализа данных»
Кластеризация. SPSS
Факультет: АВТФ
Группа: АВТ-412
Выполнили: Лазаревич М.М.
Евтушенко Н.С.
Проверила: Ганелина Н.Д.
Новосибирск
2017 г.
Цель Работы:
Познакомиться с теорией и практикой решения задачи кластеризации в среде SPSS Statistic.
Постановка задачи:
Для выбранного массива данных (в нашем случае seeds) провести кластерный анализ различными методами. Проанализировать полученные результаты.
Описание исходных данных:
Были выбраны исходные данные seeds (семена) – массив параметров зёрен трёх различных сортов пшеницы. Данный массив включает следующие параметры:
-
area А – площадь
-
perimeter P – периметр
-
compactness C = 4*pi*A/P^2 – компактность
-
length of kernel – длина зерна
-
width of kernel – ширина зерна
-
asymmetry coefficient – коэффициент асимметрии
-
length of kernel groove – длина канавки зерна
Описательные статистики:
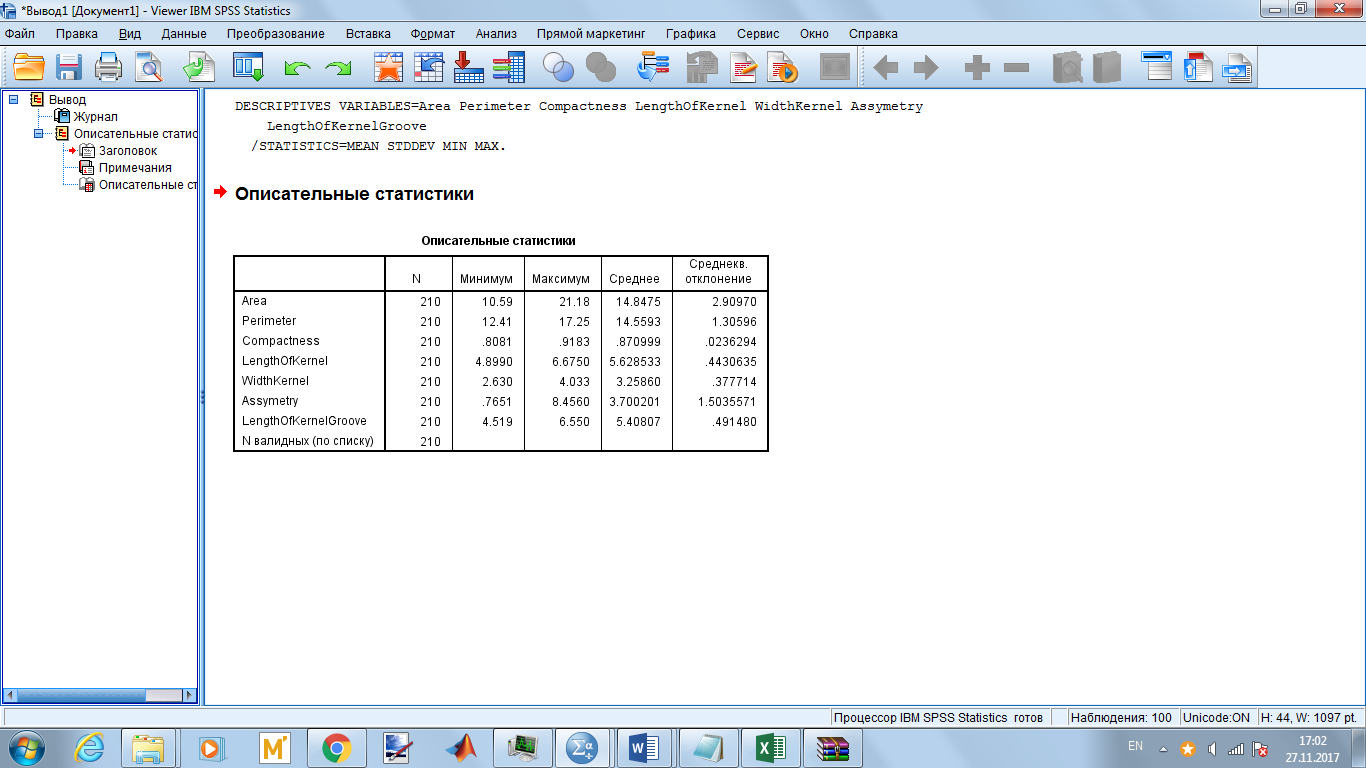
Параметр “Компактность” был исключён из анализа из-за малого отклонения значений наблюдений и прямой зависимости от других параметров.
Рисунок 1. Диаграмма рассеяния “Площадь” – “Коэффициент асимметрии”.
Рисунок 2. Диаграмма рассеяния “Длина” – “Ширина”.
Процедура применения метода:
Выполним кластеризацию методом К-средних для трёх кластеров, перед применением метода параметры наблюдений были стандартизованы.
Результаты:
|
Конечные центры кластеров |
|||
|
|
Кластер |
||
|
1 |
2 |
3 |
|
|
Zscore(Area) |
1.22360 |
-.16492 |
-1.00292 |
|
Zscore(Perimeter) |
1.23280 |
-.18537 |
-.99258 |
|
Zscore(LengthOfKernel) |
1.21703 |
-.26401 |
-.90441 |
|
Zscore(WidthKernel) |
1.12769 |
-.02827 |
-1.03957 |
|
Zscore(Assymetry) |
-.04668 |
-.78303 |
.77352 |
|
Zscore(LengthOfKernelGroove) |
1.27715 |
-.60250 |
-.64594 |
|
Расстояния между конечными центрами кластеров |
|||
|
Кластер |
1 |
2 |
3 |
|
1 |
|
3.398 |
4.845 |
|
2 |
3.398 |
|
2.283 |
|
3 |
4.845 |
2.283 |
|
|
Число наблюдений в каждом кластере |
||
|
Кластер |
1 |
69.000 |
|
2 |
68.000 |
|
|
3 |
73.000 |
|
|
Валидные |
210.000 |
|
|
Пропущенные |
.000 |
|
Рисунок 3. Распределение отклонения наблюдений от центра кластера по кластерам.
Рисунок 4. Общая гистограмма отклонений.
По полученным результатам можно сделать вывод, что точность определения кластеров наблюдений вполне приемлемая: среднее расстояние наблюдений до центра кластера в 2.2 раза меньше минимального расстояния между центрами кластеров. Данные результаты позволяют определить, к какому сорту пшеницы относятся отдельные зёрна.
Теперь необходимо провести иерархический кластерный анализа тремя различными методами, во всех методах будем использовать квадрат Евклидовой меры.
Первый метод - ближайшего соседа.
Результаты:
|
Число наблюдений в каждом кластере |
||
|
Кластер |
1 |
207 |
|
2 |
1 |
|
|
3 |
2 |
|
Среднеквадратичное отклонение от центра кластера: 5,834466
|
Расстояния между центрами кластеров |
|||
|
|
1,00000 |
2,00000 |
3,00000 |
|
1,00000 |
0 |
2,218349 |
3,482579 |
|
2,00000 |
2,218349 |
0,00000 |
1,427301 |
|
3,00000 |
3,482579 |
1,427301 |
0,00000 |
Довольно большое отклонение и тот факт, что почти все наблюдения попали в первый кластер показывают, что данный метод не годится для выбранного массива.
Второй метод - метод центроидной кластеризации:
|
Число наблюдений в каждом кластере |
||
|
Кластер |
1 |
134 |
|
2 |
74 |
|
|
3 |
2 |
|
|
Расстояния между центрами кластеров |
|||
|
|
1,00000 |
2,00000 |
3,00000 |
|
1,00000 |
0 |
4,008262 |
3,158324 |
|
2,00000 |
4,008262 |
0,00000 |
5,249318 |
|
3,00000 |
3,158324 |
5,249318 |
0,00000 |
Среднеквадратичное отклонение: 2,205815
Данный метод показывает лучшие результаты, чем предыдущий, но количество наблюдений в третьем кластере по-прежнему необычайно мало, а значит, что и этот метод скорее всего не подходит.
Третий метод - метод Уорда:
|
Число наблюдений в каждом кластере |
||
|
Кластер |
1 |
68 |
|
2 |
74 |
|
|
3 |
68 |
|
|
|
1,00000 |
2,00000 |
3,00000 |
|
1,00000 |
0 |
3,543717 |
2,174243 |
|
2,00000 |
3,543717 |
0,00000 |
4,689021 |
|
3,00000 |
2,174243 |
4,689021 |
0,00000 |
Среднеквадратичное отклонение: 1,53404
Последний метод оказался наиболее подходящим из всех трёх, результаты довольно близки к результатам применения метода К-средних, что позволяет сделать вывод о правдоподобии полученных разбиений.
Вывод:
Произошло знакомство с теорией и практикой решения задачи кластеризации в среде SPSS Statistic. Для выбранного массива данных были проведены различные кластерные анализы.