3) Предел измерений — наибольшее или наименьшее значение диапазона измерений.

4) Область рабочих частот (диапазон частот) — полоса частот, в пределах которой погрешность прибора, полученная при изменении частоты сигнала, не превышает допускаемого предела.

5) Градуировочная характеристик(цена деления) — зависимость, определяющая соотношение между сигналами на выходе и входе средства измерений в статическом режиме.

6) Чувствительность по измеряемому параметру — отношение изменения сигнала на выходе измерительного прибора к вызвавшему его изменению измеряемой величины

S= дельта У/ Дельта Х

где х — измеряемая величина; у — сигнал на выходе;

7) Предельная чувствительность— минимальная величина исследуемого сигнала, подаваемого на вход прибора, которая необходима для получения отсчета с погрешностью, не превосходящей допустимой. Наименьшее значение изменения физической величины, начиная с которого может осуществляться ее измерение, называется порогом чувствительности данного средства измерений.

8) Время измерения — время, которое требуется для определения значения измеряемой величины с заданной погрешностью.

9) Разрешающая способность (абсолютная) — минимальная разность двух значений измеряемых однородных величин, которая может быть различима с помощью прибора.

10) Быстродействие (скорость измерения) — максимальное число измерений в единицу времени, выполняемых с нормированной погрешностью.

11) Функция преобразования

12) Входной импеданс- это отношение изменения напряжения на входе к вызванному имизменению тока.

К метрологическим характеристикам средств измерений относятся те, которые оказывают влияние на результаты и погрешности измерений. Среди них можно выделить несколько основных:

• 
  градуировочные характеристики, определяющие зависимость входного сигнала от выходного; номинальное значение меры; пределы измерения; цена деления шкалы для аналоговых приборов; вид и параметры цифрового кода цифровых приборов.
  
• 
  динамические характеристики, отражающие инерционные свойства средств измерений и необходимые для оценивания динамических погрешностей.
  
• 
  инструментальные составляющие погрешности измерения.
  
• 
  функции влияния, отражающие зависимость метролог. хар-ик ср-в измерений от воздействия влияющих величин или неинформативных параметров(напряжение, частота сети и т.д.)
  

---

Метрологические хар-ки нормируются для нормальных условий применения средств измерений. Нормальными считаются такие условия, при которых изменением метролог.хар-ик под воздействием влияющих величин можно пренебречь. Инстурментальную погрешность в нормальной области значения влияющих величин называют основной.

Выход значения влияющей величины за пределы нормальной области значений может привести к возникновению значительной составляющей инструментальной погрешности, называемой дополнительной.

Классы точности средств измерений

Определенная информация о возможной инструментальной составляющей погрешности измерения необходима, хотя бы для того, чтобы выбрать средство измерений, способное измерить размер с заданной точностью. Такая информация дается указанием класса точности средства измерений.

Класс точности средства измерений– обобщенная характеристика данного типа средств измерений, как правило, отражающая уровень их точности, выражаемая пределами допускаемых основной и дополнительных погрешностей, а также другими характеристиками, влияющими на точность.

Другими словами класс точности дает возможность судить о том, в каких пределах находится погрешность средства измерений одного типа, но не является непосредственным показателем точности измерений данного средства измерения. Класс точности средства измерения устанавливают в стандартах, технических требованиях или в других нормативных документах.Для каждого класса точности определяют конкретные требования к метрологическимхарактеристикам, в совокупности определяющим уровень точности средства измерения данного класса.

Пределы допускаемых погрешностей нормируют и выражают в форме абсолютной, относительной или приведенной погрешностей. Форма выражения зависит от характера изменения погрешностей. В общем случае абсолютная погрешность состоит из аддитивной (суммируемой с измеряемой величиной) и мультипликативной (умножаемой на измеряемую величину) составляющих.

Интервальная оценка допускаемой погрешности

Максимальная основная погрешность измерительного прибора, при которой он разрешен к применению, называется пределом допускаемой основной погрешности.

1) Пределы допускаемой абсолютной основной погрешности устанавливают по одной из формул:∆=±а или ∆=±(а+bx), гд х-значение измеряемой величины, a,b-положит-ые числа, не зависящие от х.

---

Первая формула описывает аддитивную погрешность. Вторая формула –что в составе погрешности средства измерения присутствует сумма аддитивной и мультипликативной составляющих. При проведении измерений важное значение имеет диапазон измерений средства измерения. При уменьшении измеряемой величины х относительная погрешность средства измерения увеличивается и изменяется по гиперболе. Поэтому следует выбирать такой диапазон измерений, в котором значение х близко к Х_к – большему по модулю из пределов измерений.

2) Пределы допускаемой приведенной основной погрешности устанавливаются по формуле:

γ=∆/Х_N * 100%=±p, где Х_N– нормирующее значение, выраженное в тех же единицах, что и абсолютная погрешность, р – отвлеченное положит.число.

Для средств измерений с равномерной, практически равномерной или степенной шкалой значение Х_Nпринимают равным:

• 
  большему из пределов измерений или большему из модулей пределов измерений, если нулевое значение находится на краю или вне диапазона измерений
  
• 
  сумме модулей пределов измерений, если нулевое значение наход-ся внутри диапазона измерений.
  

3) Пределы допускаемой относительной основной погрешности устанавливаются по формуле:

δ=∆/х * 100%=±q, если ∆=±а q – отвлеченное положит. число.

Пределы допускаемой дополнительной погрешности.

1) Предел допускаемой абсолютной дополнительной погрешности может указываться в виде:

• 
  постоянного значения для всей рабочей области влияющей величины или постоянных значений по интервалам рабочей области влияющей величины
  
• 
  отношения предела допускаемой доп.погрешности, соответс-его регламентированному интервалу влияющей величины, к этому интервалу.
  

6. Случайные погрешности и их описание. Законы распределения и их параметры.

Аналитически случайные погрешности описывают и оценивают с помощью аппарата теории вероятностей и математической статистики.

Рассмотрим некоторые числовые характеристики случайных величин.

• 
  Математическое ожидание случайной величины – это сумма произведений всех ее возможных значений на их вероятности.математическое ожидание как дискретной так и непрерывной случайной величины есть неслучайная (постоянная) величина.Математическое ожидание приблизительно равно (тем точнее, чем больше число испытаний N) среднему арифметическому наблюдаемых значений случайной величины: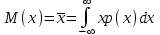
  

---

Х – обозначение случайной величины, x_i– возможное значение Х.

• 
  Для оценки рассеяния возможных значений(ширина разброса) случайной величины вокруг ее математического ожидания вводится понятие дисперсии – математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
  

• 
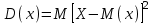
  Средним квадратическим отклонением случайной величины x называется квадратный корень из дисперсии:
  

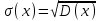
размерность среднего квадратического отклонения совпадает с размерностью самой случайной величины, поэтому в метрологии обычно используется 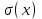, а не D(x), которая имеет размерность квадрата случайной величины.
Для характеристики частоты появления различных значений случайной величины X (в нашем случае – погрешности прибора или результата измерения с учетом и ее систематической составляющей) теория вероятностей предполагает пользоваться указанием закона распределения вероятностей различных значений этой величины.

Различают два вида законов

1) Интегральным законом или функцией распределения вероятностей F(x) случайной величины х называется функция, значение которой для любого х является вероятностью события, заключающегося в том, что случайная величина Х принимает значение, меньше х, т.е.



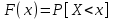
Это неубывающая функция х, изменяющаяся так, что F(-∞)=0, aF(+∞)=1. Она существует для всех случайных величин, как дискретных, так и непрерывных.

Дискретная случайная величина – величина, которая принимает отдельные изолированные возможные значения с определенными вероятностями. Число возможных значений может быть как конечным, так и бесконечным.

Непрерывная случайная величина – если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.

2) Для случайной величины с непрерывной и дифференцируемой F(x) можно найти дифференциальный закон распределения вероятностей, выражаемый как производная от F(x), т.е.p(

---

x)=F’(x)Эта зависимость называется кривой плотности распределения вероятностей. Она всегда неотрицательна, т.е. p(x)≥0 и подчиняется условию нормировки:



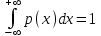
Примеры законов распределения:

• 1   2   3   4

---

Смотрите также файлы

• Как нельзя делать Подавать блюда очень горячими или холодными.docx

• График проведения суммативного оценивания.doc

• Мастерская мягкой игрушки.docx

• Ответ Взрослея, мы все чаще призадумываемся над смыслом жизни, пытаясь определить свое место в этом мире. Для нас становится важно найти свое предназначение. Ведь понимание целей во многом облегчает их достижение.doc

• При выпадениивыдергивании катетера, если вы не можете заменить его самостоятельно. Чем скорее вы обратитесь ко врачу тем лучше.docx