Таблица 2 - Дополнительные данные

i	u	V(u)	w	z	w^2	wz
1	2	5,197	0,135335	0,192419	0,018316	0,026041
2	2,5	7,78	0,082085	0,128535	0,006738	0,010551
3	3	11,14	0,049787	0,089767	0,002479	0,004469
4	3,5	15,09	0,0302	0,066269	0,000912	0,002001
5	4	19,24	0,018316	0,051975	0,000335	0,000952
6	4,5	23,11	0,011109	0,043271	0,000123	0,000481
7	5	26,25	0,006738	0,038095	0,00005	0,00026
8	5,5	28,6	0,004087	0,034965	0,00002	0,00014
9	6	30,3	0,002479	0,033003	0,00001	0,00008
	36	166,707	0,340133	0,678299	0,028971	0,044976

---

Подставляем значения в матрицу:



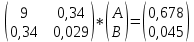
Если 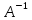 , то существует обратная матрица  . Тогда решение СЛАУ можно записать в виде: Х= 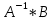, где A – матрица системы, X – столбец неизвестных, B – столбец свободных членов.

Согласно вычислениям в Excel, определитель матрицы системы равен 0,145, то есть он отличен от нуля, что является необходимым и достаточным условием существования единственного решения системы линейных алгебраических уравнений.

Для решения данного уравнения необходимо найти обратную матрицу.

Для этого можно воспользоваться функцией МОБР в Excel и тогда получим обратную матрицу:



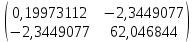
Теперь обратную матрицу нужно умножить на столбец 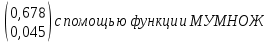. При умножении получается матрица 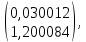которая соответствует столбцу неизвестных 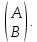То есть, иными словами, в результате вычислений мы получили, что приблизительно А=0,03, В=1,2001.

Необходимо вернуться к изначальным переменным функции :



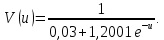
Построим график этой функции для проверки данных и сравним с исходными данными (рисунок 1):


Рисунок 1 – Сравнение графиков исходной и аппроксимирующей функций

Вывод: Отклонение аппроксимирующей функции от исходной функции на заданном множестве незначительно. Сравнение полученной модели с исходными данными позволяет понять, что выбранная модель в большей степени описывает данную зависимость.

ЗАКЛЮЧЕНИЕ

При выполнении данной практической работы мы ознакомились с новым математическим понятием «аппроксимация функций», а также рассмотрели и изучили виды и методы аппроксимации. Был сделан вывод, что аппроксимация может успешно применяется при работе с различными функциями. Данный метод позволяет производить замену сложных объектов исследования более простыми, что существенно упрощает процесс анализа некоторой исходной зависимости.

---

Функция, которая была получена при выполнении практической части данной практической работы, подходит под ситуацию, когда почти все исходные значения лежат на графике полученной аппроксимирующей функции, отсюда, эту функцию можно использовать для описания изначально данной нам зависимости между исходными данными.

Метод наименьших квадратов оказался эффективен и удобен в применении. Помимо этого, была освоена работа с матрицами в MS Excel. Таким образом, аппроксимация функции позволяет оптимизировать временные затраты при анализе определенных экономических и математических процессов.

---

Смотрите также файлы

• маркетинг.docx

• Организация высшего образования.docx

• А блімі Блімаралы таырып бойынша жиынты баалау.docx

• Задача круг уравнение неизвестная тема урока Уравнения Тема урока.pptx

• Передача информации в компьютерных сетях Требования к знаниям и умениям учащихся.docx