Добавлен: 12.01.2024
Просмотров: 63
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Ошибка отсчета превысит 0,02 если она будет заключена в интервале (0,02; 0,08). Тогда
Ответ: р=0,6
Задача 4
Исходные данные: математическое ожидание и стандартное отклонение нормально распределенного признака Х соответственно равны 10 и 2. Найти вероятность того, чтов результате испытания Х примет значение, заключенное в интервале (12, 14).
Решение.
Воспользуемся формулой
Подставив
, 
, 
, 
получим
.По таблице находим:
, 
. Искомая вероятность 
Задача 5
Исходные данные: непрерывный признак Х распределен по показательному закону, заданному плотностью вероятности
при 
и 
при 
. Найти вероятность того, что в результате испытания Х попадет в интервал 
.Решение.
Используем формулу
Учитывая, что , по условию,
; 
; 
, получим
Задача 6
Исходные данные: найти доверительный интервал для оценки с надежностью
неизвестного математического ожидания 
нормально распределенного признака 
генеральной совокупности, если генеральное стандартное отклонение 
, выборочная средняя 
, объем выборки 
.Решение.
Требуется найти доверительный интервал
Все величины, кроме
, известны. Найдем из соотношения
По таблице находим
.Подставив
, , , , окончательно получим доверительный интервал
Задача 7
Исходные данные: используя критерий Пирсона, при уровне значимости
установить, случайно или значимо расхождение между эмпирическими частотами 
и теоретическими частотами 
, которые вычислены, исходя из гипотезы о нормальном распределении генеральной совокупности Х:
 | 8 | 16 | 40 | 72 | 36 | 18 | 10 |
 | 6 | 18 | 36 | 76 | 39 | 18 | 7 |
Решение.
Найдем наблюдаемое значение критерия Пирсона:
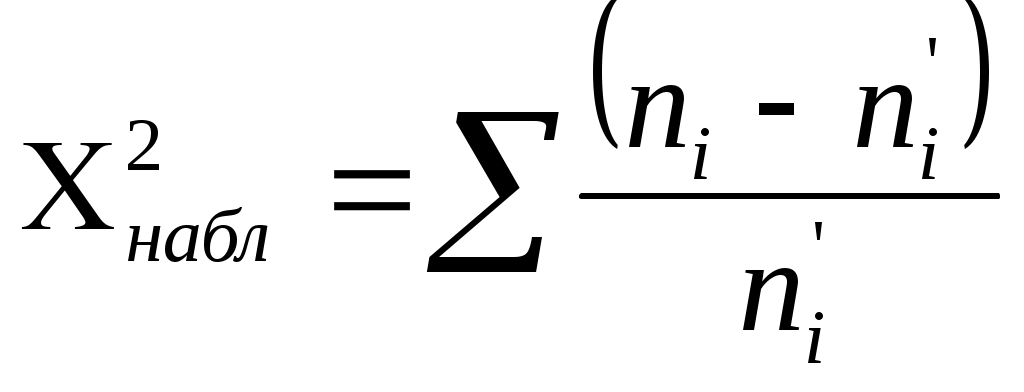
Для этого составим расчетную таблицу
 | | |  |  |  |
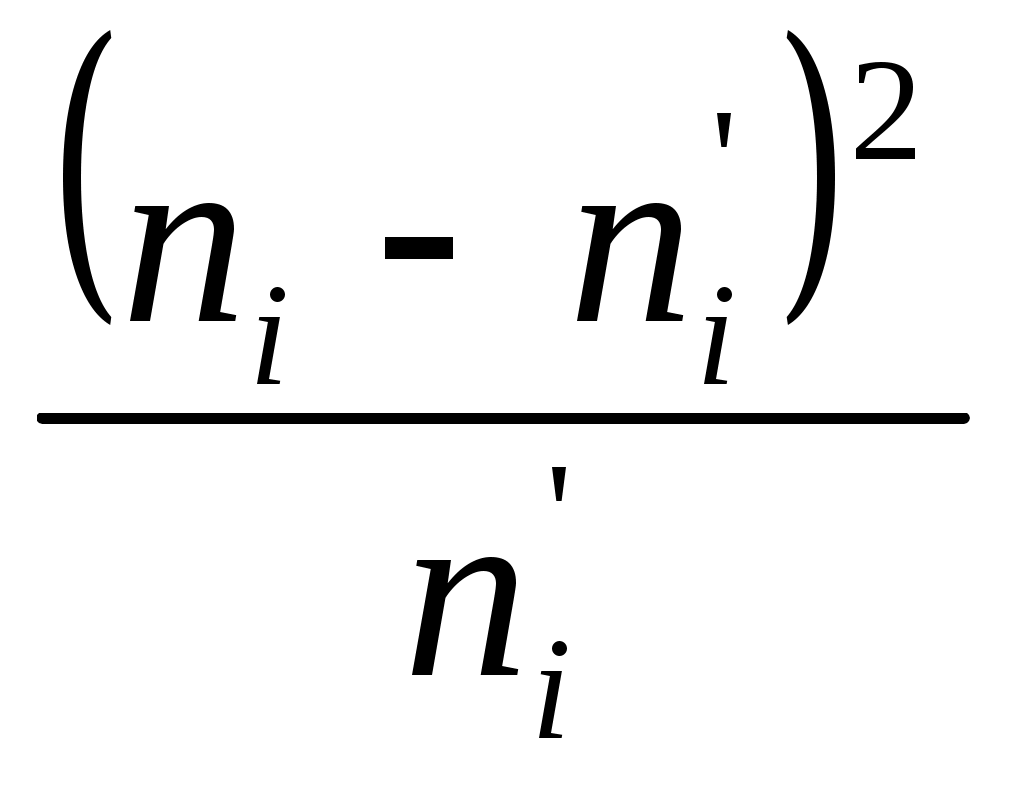| 1 | 8 | 6 | 2 | 4 | 0,667 |
| 2 | 16 | 18 | -2 | 4 | 0,222 |
| 3 | 40 | 36 | 4 | 16 | 0,444 |
| 4 | 72 | 76 | -4 | 16 | 0,211 |
| 5 | 36 | 39 | -3 | 9 | 0,231 |
| 6 | 18 | 18 | 0 | 0 | 0 |
| 7 | 10 | 7 | 3 | 9 | 1,286 |
 | 200 | | | |  |
По таблице критических точек распределения
, по уровню значимости 
и числу степеней свободы 
находим критическую точку 
. Так как 
, то нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности. Другими словами, расхождение между эмпирическими и теоретическими частотами незначимо (случайно).