Файл: Контроль обучения 4 Первое контрольное задание 5 Второе контрольное задание 31.doc

Цифровой корень находится суммой через сумму цифр числа до тех пор, пока эта сумма сама не станет цифрой. Например, для числа 9999999 цифровой корень находится так:

9+9+9+9+9+9+9 = 63;

6+3 = 9.

Цифровой корень 9999999 равен девяти.
Переменные:

а) в функции num:

n – целое число (глобальная переменная);

s – вспомогательная переменная (локальная переменная);

б) в функции root:

n – целое число (глобальная переменная);

в) в основной программе:

n – целое число (глобальная переменная).
Алгоритм решения задачи:

1. 
   создаем описание функций num и root;
   
2. 
   вводим целое число n;
   
3. 
   вызываем рекурсивную функцию root и определяем цифровой корень числа n;
   
4. 
   завершаем работу программы.
   

var n:longint;

function num(i:longint):integer;

var s: integer;

begin

s:=0;

repeat

s:=s+n mod 10;

n:= n div 10;

until n=0;

num:=s;

end;

function root(l:longint):integer;

begin

if n<10 then root:=n

else

begin

n:=num(n);

root:=root(n);

end;

end;
begin

write('Введите целое число n=');

readln(n);

writeln('Его цифровой корень равен : ', root(n));

end.
6. Напишите рекурсивную программу вычисления суммы
var n : integer;

function sum(i : integer) : real;

begin

if i=1 then sum:=0 else sum:=sum(i–1)+i*i+i+5;

end;
begin

writeln('Введите n');

readln(n);

writeln('Значение суммы равно – ', sum(n));

end.
ПРОГРАММЫ, РАБОТАЮЩИЕ В ГРАФИЧЕСКОМ РЕЖИМЕ
7. Построить семейство одинаковых окружностей, центры которых лежат на вертикально вращающемся отрезке, верхний конец которого закреплен.
Переменные:

x, y – координаты центра очередного маленького круга;

y0 – смещение кругов по вертикале;

i – переменная цикла;

t – угол поворота;

drive – тип графического драйвера;

mode – режим работы графического адаптера.
Для решения задачи:

1. 
   инициируем модуль graph;
   
2. 
   устанавливаем начальные значения радиуса, координаты центра;
   
3. 
   организуем цикл, в котором закрашиваем круги со все большим радиусом до тех пор, пока не будет нажата любая клавиша.
   

uses crt,graph;

var drive,mode,x,y,i,t,y0:integer;

begin

drive:=detect;

initgraph(drive,mode,'c:\tp\bgi');

setfillstyle(1,1);

floodfill(1,4,1);

t:=–4;

y0:=10;

setcolor(16);

for i:=1 to 150 do

begin

t:=t+2;

y0:=y0+3;

x:=getmaxx div 2 + trunc(cos(t/10)*i);

y:=y0 – trunc(sin(t/10)*i);

setfillstyle(1,14);

fillellipse(x,y,20,20);

delay(100);

end;

repeat

until keypressed;

closegraph;

end.

8. Построить движущиеся изображения НЛО на фоне звездного неба.

---

8.1 Переменные:

x, y – случайные координаты;

r – радиус;

i – переменная цикла;

drive – тип графического драйвера;

mode – режим работы графического адаптера.
Алгоритм решения задачи:

1. 
   инициируем модуль graph;
   
2. 
   организуем безусловный цикл по переменной i и рисуем звездное небо;
   
3. 
   организуем цикл до тех пор, пока не будет нажата любая клавиша;
   
4. 
   в этом цикле рисуем НЛО с помощью двух эллипсов, двух линий и двух маленьких кружочков, держим на экране, затем стираем изображение процедурой CLEARDEVICE;
   
5. 
   опять рисуем звездное небо;
   
6. 
   определяем случайным образом координаты следующего изображения НЛО;
   
7. 
   после нажатия любой клавиши закрываем графический режим.
   

uses crt,graph;

var drive,mode,x,y,i,r:integer;

begin

r:=40;

x:=r*5;

y:=r*2;

drive:=detect;

initgraph(drive,mode,'c:\tp\bgi');

setcolor(3);

for i:=1 to 600 do

putpixel(random(i),random(i),i);

repeat

ellipse(x,y,0,360,r,(r div 3)+2);

ellipse(x,y–4,190,357,r,r div 3);

line(x–17,y–16,x–25,y–22);

line(x+17,y–16,x+25,y–22);

circle(x+25, y–25,2);

circle(x–25, y–25,2);

setfillstyle(1,3);

floodfill(x+1,y+4,3);

delay(150);

cleardevice;

for i:=1 to 600 do

putpixel(random(i),random(i),i);

x:=x+random(10);

y:=y+random(10);

until (keypressed);

closegraph;

end.

8.2 Та же программа может быть написана с использованием пары процедур GETIMAGE(lx,ly,rx,ry,saucer^) и PUTIMAGE(x,y,saucer^,xorput).

Процедура GETIMAGE(lx,ly,rx,ry,saucer^) помещает изображение в буфер, а PUTIMAGE(x,y,saucer^,xorput) выводит в заданное место изображение.

Параметр xorput определяет способ вывода на экран – исключающее ИЛИ.

Например, операторами

GETIMAGE(lx,ly,rx,ry,saucer^);

READLN;

PUTIMAGE(x,y,saucer^,xorput);

мы выводим изображение на экран и после нажатия любой клавиши стираем его.

Можно использовать другие способы вывода изображения на экран, например:

NORMALPUT – стирает часть экрана и на это место выводит изображение;

NOTPUT – делает то же самое, но изображение инвертируется;

ORPUY – дописывает новое изображение.

Переменные:

x, y – случайные координаты;

r – радиус;

i – переменная цикла;

saucer – указатель буфера хранения изображения;

drive – тип графического драйвера;

mode – режим работы графического адаптера.
Алгоритм решения задачи:

1. 
   инициируем модуль graph;
   
2. 
   рисуем НЛО с помощью двух эллипсов, двух линий и двух маленьких кружочков, держим на экране, затем стираем изображение процедурой CLEARDEVICE;
   
3. 
   определяем размер буфера и помещаем в него изображение;
   
4. 
   организуем безусловный цикл по переменной i и рисуем звездное небо;
   
5. 
   организуем цикл до тех пор, пока не будет нажата любая клавиша;
   
6. 
   опять рисуем звездное небо;
   
7. 
   в этом цикле помещаем изображение из буфера на экран, держим его на экране, затем стираем изображение;
   
8. 
   определяем случайным образом координаты следующего изображения НЛО;
   
9. 
   после нажатия любой клавиши закрываем графический режим.
   

---

uses crt,graph;

var drive,mode,x,y,i,r,rx,ry,lx,ly,size:integer;

saucer:pointer;

begin

r:=20;

x:=r*5;

y:=r*2;

drive:=detect;

initgraph(drive,mode,'c:\tp\bgi');

setcolor(3);

ellipse(x,y,0,360,r,(r div 3)+2);

ellipse(x,y–4,190,357,r,r div 3);

line(x–17,y–16,x–25,y–22);

line(x+17,y–16,x+25,y–22);

circle(x+25, y–25,2);

circle(x–25, y–25,2);

setfillstyle(1,3);

floodfill(x+1,y+4,3);

lx:=x–r–30;

ly:=y–30;

rx:=x+r+30;

ry:=y+r div 3+30;

size:=imagesize(lx,ly,rx,ry);

getmem(saucer,size);

getimage(lx,ly,rx,ry,saucer^);

readln;

putimage(lx,ly,saucer^,xorput);

for i:=1 to 600 do

putpixel(random(i),random(i),i);

repeat

putimage(x,y,saucer^,xorput);

delay(150);

putimage(x,y,saucer^,xorput);

x:=x+random(10);

y:=y+random(10);

until (keypressed);

readln;

closegraph;

end.

9. Построить астроиду-кривую, заданную параметрическим уравнением x = b cos ³(t), y = b sin ³(t), t принадлежит интервалу [0, 2] (рис. 1).




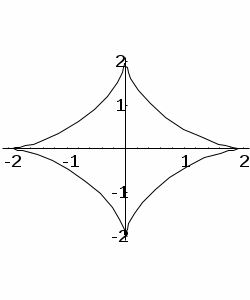
Рис. 1 – Астроида


uses crt,graph;

const B=200;

var drive,mode,i:integer;

x,y,t:real;

begin

drive:=detect;

initgraph(drive,mode,'c:\tp\bgi'); {инициализация графического режима}

setcolor(3);

line(10,240,630,240); {ось X}

line(320,10,320,470); {ось Y}

line(630,240,610,235); {стрелки на оси X}

line(630,240,610,245);

line(320,10,315,30); {стрелки на оси Y}

line(320,10,325,30);

t:=0;

while t<=2*pi do

begin

x:=b*sqr(cos(t))*cos(t); {рассчитываем по формуле координаты точек}

y:=b*sqr(sin(t))*sin(t);

x:=320+x; y:=240+y; {рисуем в центре экрана}

{рисуем точку с координатами x, y}

putpixel(round(x),round(y),random(15)); t:=t+0.001;

end;

repeat until keypressed;

closegraph;

end.
Варианты заданий

Вариант 1	Задача 1 type ряд = file of integer; Описать процедуру p(f,g) от двух файлов типа ряд, которая в пустой файл f переписывает положительные элементы файла g. Указание: введите файл g (последний элемент равен 0). Выполните процедуру p(f,g). Распечатайте файл f. Задача 2 Пусть для целого n>0 функция s(n) равна сумме цифр числа n. Дано m>0. Упорядочить все числа n от 1 до m в порядке невозрастания значений s(n). Указание: использовать только один массив длиной m. Задача 3 Напишите рекурсивную подпрограмму, которая печатает в обратном порядке заданную строку. Задача 4 Напишите программу для графической иллюстрации сортировки массива алгоритмом простого выбора. Массив изобразите в виде диаграммы – каждый элемент массива представляется в виде столбика, высота которого пропорциональна значению элемента. Визуализация сортировки сводится к показу массива после каждого перемещения элементов.
Вариант 2	Задача 1 type fr = file of real; Описать процедуру predlast(f), значением которой является предпоследний элемент файла f, имеющего тип fr и содержащего не менее двух элементов. Указание: введите файл f (последний элемент = 0) и вычислите функцию predlast(f). Задача 2 Дан массив a: array [1..n] of integer. Упорядочить элементы массива а по неубыванию в соответствии со следующим критерием: элемент x считается «больше» элемента y, если первая цифра числа x больше первой цифры y. Задача 3 type reals = file of real; var f : reals; Опишите рекурсивную функцию sum без параметров для нахождения суммы элементов файла f. Задача 4 Построить эпициклоиду – кривую, заданную параметрическим уравнением x = (a+b) cos(t) – a cos((a+b) t/a), y = (a+b) sin(t) – a sin((a+b) t/a), a>0, b>0, b 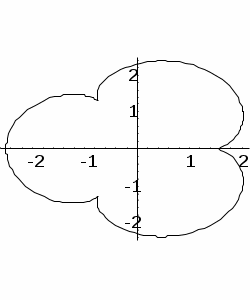/a – целое положительное число, t принадлежит интервалу [0,2].
Вариант 3	Задача 1 type rad = file of integer; Описать процедуру p(f,g) от двух файлов типа rаd, которая из файла f переписывает в пустой файл g сначала все положительные числа, а потом все отрицательные. Указание: введите файл f (последний элемент равен 0). Выполните процедуру p(f,g). Распечатайте файл g. Задача 2 Пусть для целого n>0 функция d(n) равна наименьшему делителю числа n, не равному 1. Дано m>0. Упорядочить все числа n от 1 до m в порядке неубывания значений d(n). Указание: использовать только один массив длиной m. Задача 3 Описать рекурсивную функцию letter (s), которая подсчитывает количество букв в строке s. Задача 4 Построить лемнискату – кривую, уравнение которой в полярных координатах 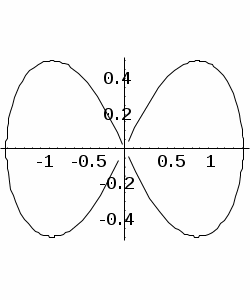 = , a>0.
Вариант 4	Задача 1 type seria = file of integer; Описать функцию prod(s) с вещественным значением, подсчитывающую произведение ненулевых элементов файла s. Указание: введите файл s (последний элемент равен 0) и напечатайте значение функции prod(s). Задача 2 Дана действительная матрица размером MN. Пусть для каждой строки матрицы определена функция f(a), равная сумме нечетных элементов строки a. Упорядочить (переставить) строки матрицы по неубыванию в соответствии со следующим критерием: строка a считается «больше» строки b, если f(a) > f(b). Используйте алгоритм простого выбора. Задача 3 Напишите рекурсивную программу, которая n раз выводит на экран текст истории о попе и его собаке (рассказ в рассказе). Задача 4 Построить строфоиду – кривую, заданную параметрическим уравнением x = a(t 2 – 1)/(t 2 + 1), y = at (t 2 – 1)/(t 2 +1), a>0, t принадлежит интервалу [– , + ].
В 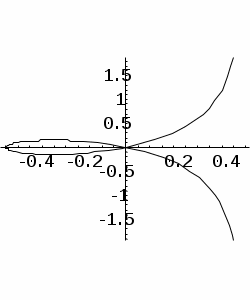ариант 5	Задача 1 type seria = file of integer; var s:seria; Описать функцию max(s), вычисляющую значение максимального элемента файла s. Указание: введите файл s (последний элемент равен 0) и напечатайте значение функции max(s). Задача 2 Дана целочисленная матрица размером MN. Пусть для каждой строки матрицы определена функция f(a), равная количеству простых чисел среди элементов строки a. Упорядочить (переставить) строки матрицы по невозрастанию в соответствии со следующим критерием: строка a считается «больше» строки b, если f(a) > f(b). Используйте алгоритм простого выбора. Задача 3 Во входном файле задана непустая последовательность положительных вещественных чисел, за которой следует отрицательное число. Описать рекурсивную функцию sum без параметров для нахождения суммы этих положительных чисел. Задача 4 Построить кривую «улитку Паскаля» по заданному параметрическому уравнению x = a cos 2 (t) + b cos(t), y = a cos(t) sin(t) + b sin(t), a>0, b>0, t принадлежит интервалу [0, 2]. Рассмотреть три случая: 1) b >= 2a (см. рис.); 2) a < b< 2a; 3) a > b.
В 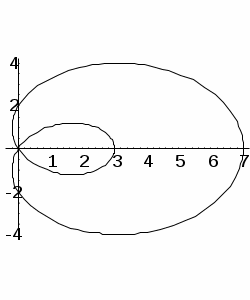ариант 6	Задача 1 Описать логическую функцию check(s) для текстового файла s, проверяющую, содержит ли файл s латинские буквы. Указание: введите файл s (последний элемент в файле '.') и вычислите значение функции check(s). Задача 2 Дана целочисленная матрица размером MN. Пусть для каждой строки матрицы определена функция f(a), равная сумме составных чисел, являющихся элементами строки a. Упорядочить (переставить) строки матрицы по неубыванию в соответствии со следующим критерием: строка a считается «больше» строки b, если f(a) > f(b). Используйте алгоритм простого выбора. Задача 3 type reals = file of real; var f : reals; Напишите рекурсивную программу, которая печатает сначала все отрицательные элементы этого файла, а затем положительные (в любом порядке). Задача 4 Соединить конечное множество точек на плоскости замкнутой ломаной линией без самопересечений с вершинами в этих точках. (Полный перебор не делать; ответом будет порядок обхода точек плоскости.) Указание: перейти к полярным координатам и упорядочить точки по значениям угла, а для точек с одинаковым значением угла – по расстоянию до полюса.
Вариант 7	Задача 1 Для файла s, состоящего из целых чисел, определите процедуру, которая находит значения максимального и минимального элементов файла s. Указание: введите файл s (последний элемент равен 0) и напечатайте значения максимального и минимального элементов файла s. Задача 2 Дана действительная матрица размером MN. Пусть для каждой строки матрицы определена функция f(a), равная индексу наименьшего элемента в строке a. Упорядочить (переставить) строки матрицы по возрастанию в соответствии со следующим критерием: строка a считается «больше» строки b, если f(a) > f(b). Используйте алгоритм простого выбора. Задача 3 const n=...; type vector = array [1..n] of real; Описать функцию min (x) для определения минимального элемента вектора x, введя вспомогательную рекурсивную функцию min1 (k), находящую минимум среди последних элементов вектора x, начиная с k-го. Указание: пусть min(x) – функция, которая вычисляет минимум среди элементов массива x, а min1(k) – функция, которая вычисляет минимум среди элементов xk, xk+1, …, xn массива x (для этой функции массив x есть глобальная переменная, определенная в главной программе). Имеем равенство min(x) = min1(1). Определим функцию min1(k) рекурсивно: если k=n, то функция возвращает результат xn; если kk и min1(k+1) (второе число получается при рекурсивном вызове). Задача 4 Даны целые числа t1, t2, ... t31, – задающие график температур за март месяц. Построить график температур. Отрезки прямых, лежащие выше 0 градусов Цельсия и лежащие ниже 0 градусов Цельсия, должны быть окрашены в разные цвета.
Вариант 8	Задача 1 type rad = file of 1..maxint; Описать процедуру prim(f,n), записывающую в файл f все простые числа 2,3,5,7,11,13,17..., не превосходящие целого положительного числа n. Указание: введите n. Выполните процедуру prim(f,n). Распечатайте файл f. Задача 2 Дана действительная матрица размером MN. Пусть для каждой строки матрицы определена функция s(a), равная разности между максимальным и минимальным элементами строки a. Упорядочить (переставить) строки матрицы по неубыванию значений функции s(a). Используйте алгоритм простого выбора. Задача 3 const n=...; type vector = array [1..n] of real; Описать функцию max (x) для определения максимального элемента вектора x, введя вспомогательную рекурсивную функцию max1 (k), находящую максимум среди первых k элементов вектора x. Указание: пусть max(x) – функция, которая вычисляет максимум среди элементов массива x, а max1(k) – функция, которая вычисляет максимум среди элементов xk, xk+1, …, xn массива x (для этой функции массив x есть глобальная переменная, определенная в главной программе). Имеем равенство max (x) = max1(1). Определим функцию max1(k) рекурсивно: если k=n, то функция возвращает результат xn; если kk и max1(k+1) (второе число получается при рекурсивном вызове). Задача 4 Построить кривую кардиоиду по заданному параметрическому уравнению x = a cos t (1+ cos t), y = a sin t (1 + cos t), a>0, t  [0, 2).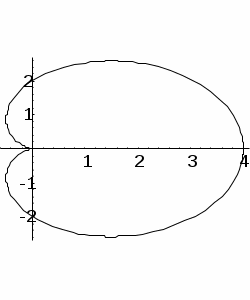
Вариант 9	Задача 1 type ряд = file of integer; Описать процедуру append(f,g,h) от трех файлов типа ряд, которая записывает в файл f сначала все элементы файла g, а затем все элементы файла h. Указание: введите два файла g и h. Выполните процедуру append(f,g,h). Напечатайте файл f. Задача 2 Дана матрица A из целых чисел размером MN. Переставить строки матрицы так, чтобы строки стали расположены по возрастанию в лексикографическом порядке. Задача 3 Дан массив a : array [1..n] of integer; Напишите рекурсивную программу для вычисления суммы Указание: Пусть функция f(k) вычисляет сумму 1/a[1]+1/a[2]+…+1/a[k]. Нам надо вычислить f(n). Определим f(k) рекурсивно: если k=1, то f(k)=1/a[1]; если k>1, то значение функции равно сумме 1/a[k] и f(k–1). Задача 4 Построить кривую циссоиду по заданному параметрическому уравнению x = a t2/(1+t2), y = a t3 /(1 + t2), a>0, t  (–, ).
В 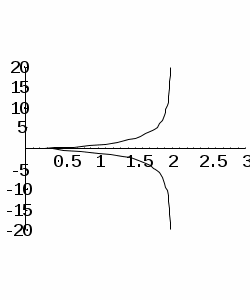ариант 10	Задача 1 Type fr = file of real; Описать функцию s3(f), значением которой является сумма последних трех элементов файла f, имеющего тип fr и содержащего не менее 3 элементов. Указание: введите файл f (последний элемент = 0) и вычислите функцию s3(f). Задача 2 Дана матрица A из целых чисел размером MN. Переставить строки матрицы так, чтобы строки стали расположены по убыванию в лексикографическом порядке. Задача 3 type reals = file of real; var f : reals; Опишите рекурсивную функцию sum (n) для нахождения суммы , где a[ i ] – элемент файла f. Указание. Пусть функция f(k) вычисляет сумму a[1]n+a[2]n+…+a[k]n. Нам надо вычислить f(n). Определим f(k) рекурсивно: если k=1, то f(k)=a[1]n; если k>1, то значение функции равно сумме a[k]n и f(k–1). Задача 4 Построить спираль вокруг начала координат с n витками и внешним радиусом r; начальное направление спирали образует с осью x угол . Параметрическое представление спирали: x = r cos t, y = r sin t, r = t/2, t2 n.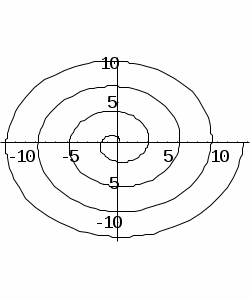
Вариант 11	Задача 1 type seria = file of integer; var s:seria; Описать функцию poz(s), подсчитывающую количество положительных чисел в файле s. Указание: введите файл s (последний элемент равен 0) и напечатайте значение функции poz(s). Задача 2 Дана действительная матрица размером MN. Упорядочить (переставить) строки матрицы по убыванию значений наибольших элементов строк. Используйте алгоритм простого выбора. Задача 3 Напишите рекурсивную программу для вычисления суммы . Указания. Пусть функция f(k) вычисляет сумму a[1]*a[2]*…a[k]. Нам надо вычислить f(n). Определим f(k) рекурсивно: если k=1, то f(k)=a[1]; если k>1, то значение функции равно сумме a[k] и f(k–1). Задача 4 Напишите программу для графической иллюстрации сортировки массива алгоритмом «пузырька». Массив изобразите в виде диаграммы – каждый элемент массива представляется в виде столбика, высота которого пропорциональна значению элемента. Визуализация сортировки сводится к показу массива после каждого перемещения элементов.
Вариант 12	Задача 1 Описать процедуру letter(s,t), которая записывает в текстовый файл t все латинские буквы из строки s. Указание: введите строку s. Выполните процедуру letter(s,t) и распечатайте элементы файла t. Задача 2 Дана действительная матрица размером MN. Упорядочить (переставить) строки матрицы по возрастанию значений первых элементов строк. Используйте алгоритм простого выбора. Задача 3 Функция f (n) определена для целых положительных чисел следующим образом: 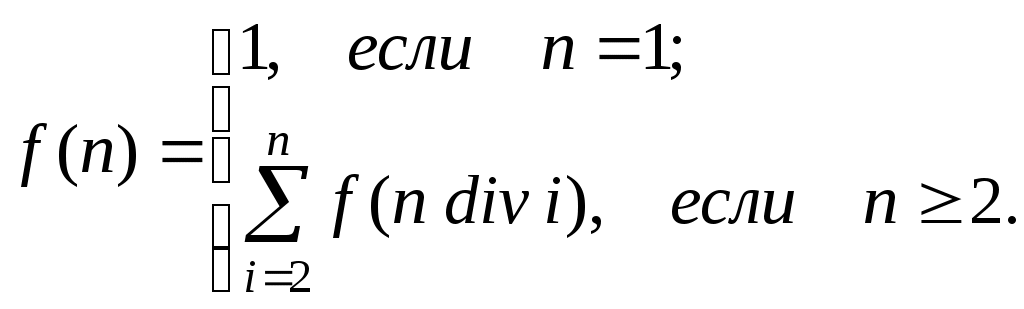Вычислить f (k) для k=15, 16,..., 30. Задача 4 Напишите программу для графической иллюстрации сортировки массива алгоритмом простых включений. Массив изобразите в виде диаграммы – каждый элемент массива представляется в виде столбика, высота которого пропорциональна значению элемента. Визуализация сортировки сводится к показу массива после каждого перемещения элементов.
Вариант 13	Задача 1 type reals = file of real; Описать процедуру p(f,g,h) от трех файлов типа reals, которая переписывает из файла f в непустой файл g все элементы, меньшие среднего арифметического всех элементов файла f, и в непустой файл h записывает все остальные числа. Указание: введите файл f (последний элемент = 0). Выполните процедуру p(f,g,h). Распечатайте файлы g и h. Задача 2 Дана действительная матрица размером MN. Упорядочить (переставить) строки матрицы по убыванию сумм элементов строк. Используйте алгоритм простого выбора. Задача 3 Напишите рекурсивную программу для вычисления суммы . Указание: Пусть функция f(k) вычисляет сумму a[1]*a[2]*…a[k]. Нам надо вычислить f(n). Определим f(k) рекурсивно: если k=1, то f(k)=a[1]; если k>1, то значение функции равно сумме a[k] и f(k–1). Задача 4 Напишите программу для графической иллюстрации сортировки массивов алгоритмом слияния. Массивы изобразите в виде диаграммы – каждый элемент массива представляется в виде столбика, высота которого пропорциональна значению элемента. Визуализация сортировки сводится к показу массивов после каждого перемещения элементов.
Вариант 14	Задача 1 Дан текстовый файл, в котором строки содержат как латинские буквы, так и цифры. Необходимо создать другой текстовый файл, содержащий строки из первого, преобразованные по следующему принципу: в начале строки расположены все буквы исходной строки, а затем все цифры (в том же порядке). Описать процедуру letter(s,t), которая записывает в текстовый файл t сначала все латинские буквы из строки s, а затем все цифры. Указание: введите исходный файл. Выполните процедуру letter(s,t) и распечатайте элементы файла t. Задача 2 Дана действительная матрица размером MN. Упорядочить (переставить) строки матрицы по убыванию значений последних элементов строк. Используйте алгоритм простого выбора. Задача 3 Дан массив a : array [1..n] of integer; Напишите рекурсивную программу для вычисления произведения . Указание. Пусть функция f(k) вычисляет произведение a[1]*a[2]*…a[k]. Нам надо вычислить f(n). Определим f(k) рекурсивно: если k=1, то f(k)=a[1]; если k>1, то значение функции равно произведению a[k] и f(k–1). Задача 4 Напишите программу, которая имитирует движение велосипеда. Указание: напишите процедуру отображения велосипеда с параметрами. В качестве параметра возьмите координаты какой-нибудь точки велосипеда (например, середина педалей – x1, y1). Назовем данную точку «центральной». Построение велосипеда ведите относительно центральной точки (например, чтобы нарисовать колесо велосипеда, можно воспользоваться следующим действием: circle(x1+50,y1,25)). Перемещение велосипеда по экрану можно получить, реализовав, например, следующий алгоритм: Задаем начальные значения переменным x1 и y1. Рисуем велосипед заданным цветом с данными значениями x1 и y1 (вызываем процедуру рисования велосипеда). Изменяем цвет линий на цвет, соответствующий цвету фона. Рисуем велосипед измененным цветом с теми же значениями x1 и y1 (вызываем процедуру рисования велосипеда). Изменяем координаты x1. Изменяем цвет линий на цвет, соответствующий цвету велосипеда. Рисуем велосипед заданным цветом с новыми значениями x1 и y1 (вызываем процедуру рисования велосипеда). Повторяем действия 2–7.
Вариант 15	Задача 1 type seria = file of integer; var s:seria; Описать функцию poz(s, n), подсчитывающую количество положительных и отрицательных чисел в файле s. Указание: введите файл s (последний элемент равен 0) и напечатайте значение функции poz(s, n). Задача 2 Дана целочисленная матрица размером MN. Пусть для каждой строки матрицы определена функция f(a), равная сумме простых чисел, являющихся элементами строки a. Упорядочить (переставить) строки матрицы по неубыванию в соответствии со следующим критерием: строка a считается «больше» строки b, если f(a) > f(b). Используйте алгоритм простого выбора. Задача 3 Описать рекурсивную функцию digits (s), которая подсчитывает сумму цифр в строке s. Задача 4 Написать программу, вызывающую пульсацию окружности в центре экрана. Окружность должна увеличиваться в диаметре до тех пор, пока не достигнет границ экрана, затем она начинает сжиматься. Процесс должен циклически повториться, при этом необходимо обеспечить чередование цветов при увеличении и уменьшении диаметра окружности.

---

10>0>

---