Добавлен: 12.01.2024
Просмотров: 183
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
– частота повторения i-ых вариантов признака – вес.
Рассчитаем среднюю арифметическую взвешенную по данным табл. 4.
Таблица 4
Группировка областей по населению ЦФО
Хср = 19245/16 = 1203 чел.
Рассчитаем структурные средние.
К структурным средним относятся мода и медиана.
Для вычисления моды в интервальном ряду применяется формула:
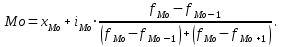
Mo = 981+338*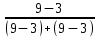
= 1150чел.
Значение медианы определяется по формуле:
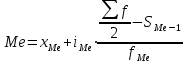
Ме = 981+338*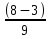
= 1168 чел.
Вывод: В среднем численность населения в областях ЦФО в 2017г. составляет 1213 человек на 1 область. Чаще всего на 1 область приходится 1150 человек. В половине областей эта величина больше 1168 человек, в другой половине – меньше.
2.3. Определение значений показателей вариации численности населения ЦФО в 2017г.
Расчет проведем по данным таблицы 5.
Таблица 5
Показатели вариации численности населения ЦФО в 2017г.
Хср=19245/16=1203 чел.
Рассчитаем показатели вариации:
1) Размах или амплитуда вариации R (абсолютная разность между максимальным и минимальным значениями признаков изучаемой совокупности):
R=Хmax - Хmin = 1995-812=1183 чел.
2) Дисперсия σ2 (средний квадрат отклонений вариантов от их средней величины):
= 
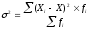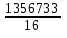= 84795,8
3) Среднее квадратическое отклонение σ (обобщающая характеристика размеров вариации признака в совокупности):
= 
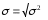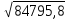= 291,2
4) Коэффициент вариации:
= 
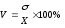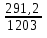= 0,24%
Вывод: коэффициент вариации меньше 33%, что показывает ненадежность совокупности и средней величины, равной 1327 человек.
2.4. Анализ рядов динамики численности населения ЦФО в 2017г.
Ряд динамики – последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления.
Для проведения анализа выберем интервальный динамический ряд – численности населения ЦФО (табл. 6).
Таблица 6
Аналитические показатели ряда динамики
Средние показатели динамики.
1. Средний уровень динамического ряда (для интервального ряда с равностоящими уровнями):
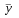= Σ уi / n = 234074/6 = 39012 чел.
2. Средний абсолютный прирост:
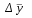= Σ∆уiц / n-1 = 632/5 = 126 чел.
3. Средний темп роста:
=
=
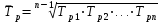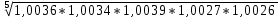*100 = 100,81=101%
4. Средний темп прироста:
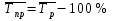= 101% - 100% = 1%
5. Среднее абсолютное значение 1% прироста:
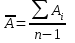
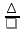= 126/1 = 126 чел.
Вывод: За анализируемый период численность населения ЦФО выросла на 632 человека. В среднем за месяц темп роста численности населения ЦФО составил 101% или в абсолютном выражении 126 человек, что определило его средний прирост в размере 1% в год.
Применим метод аналитического выравнивания. Выравнивание происходит по методу наименьших квадратов.
В зависимости от года t численности населения ЦФО изменяется по закону:
Yt =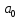
+
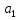*t, где 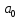, 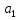– параметры уравнения регрессии.
Найдем параметры уравнения регрессии, решив систему уравнений, составленную по методу наименьших квадратов:
= 
= 
= 
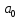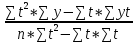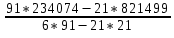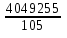= 38564.3
=
= 
= 
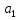
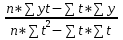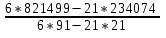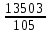= 128.6
Промежуточные значения расчетов приведены в таблице 7.
Таблица 7
Аналитическое выравнивание
Рассчитаем среднюю арифметическую взвешенную по данным табл. 4.
Таблица 4
Группировка областей по населению ЦФО
| Интервалы | Середина интервала | Всего областей | Накопленная частота | X*F |
| 643-981 | 812 | 3 | 3 | 2436 |
| 981-1319 | 1150 | 9 | 12 | 10350 |
| 1319-1657 | 1488 | 3 | 15 | 4464 |
| 1657-2333 | 1995 | 1 | 16 | 1995 |
| | Всего | 16 | | 19245 |
Хср = 19245/16 = 1203 чел.
Рассчитаем структурные средние.
К структурным средним относятся мода и медиана.
Для вычисления моды в интервальном ряду применяется формула:
Mo = 981+338*
= 1150чел.Значение медианы определяется по формуле:
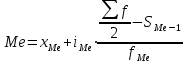
Ме = 981+338*
= 1168 чел.Вывод: В среднем численность населения в областях ЦФО в 2017г. составляет 1213 человек на 1 область. Чаще всего на 1 область приходится 1150 человек. В половине областей эта величина больше 1168 человек, в другой половине – меньше.
2.3. Определение значений показателей вариации численности населения ЦФО в 2017г.
Расчет проведем по данным таблицы 5.
Таблица 5
Показатели вариации численности населения ЦФО в 2017г.
| Интервалы | Всего областей | Середина интервала | x*f | x - ẋ | (x - ẋ)² | (x - ẋ)² * f |
| 643-981 | 3 | 812 | 2436 | -380 | 144400 | 433200 |
| 981-1319 | 9 | 1150 | 10350 | -42 | 1764 | 15876 |
| 1319-1657 | 3 | 1488 | 4464 | 296 | 87616 | 262848 |
| 1657-2333 | 1 | 1995 | 1995 | 803 | 644809 | 644809 |
| Всего | 16 | - | 19245 | 677 | - | 1356733 |
Хср=19245/16=1203 чел.
Рассчитаем показатели вариации:
1) Размах или амплитуда вариации R (абсолютная разность между максимальным и минимальным значениями признаков изучаемой совокупности):
R=Хmax - Хmin = 1995-812=1183 чел.
2) Дисперсия σ2 (средний квадрат отклонений вариантов от их средней величины):
= = 84795,83) Среднее квадратическое отклонение σ (обобщающая характеристика размеров вариации признака в совокупности):
= = 291,24) Коэффициент вариации:
= = 0,24%Вывод: коэффициент вариации меньше 33%, что показывает ненадежность совокупности и средней величины, равной 1327 человек.
2.4. Анализ рядов динамики численности населения ЦФО в 2017г.
Ряд динамики – последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления.
Для проведения анализа выберем интервальный динамический ряд – численности населения ЦФО (табл. 6).
Таблица 6
Аналитические показатели ряда динамики
| Год | Кол-во чел | Абсолютный прирост | Темпы роста, % | Темпы прироста, % | Абсолютное значение 1% прироста | |||
| б | ц | б | ц | б | ц | |||
| 2012 | 38679 | - | - | - | - | - | - | - |
| 2013 | 38820 | 141 | 141 | 100,36 | 100,36 | 0,36 | 0,36 | 391,7 |
| 2014 | 38951 | 272 | 131 | 100,70 | 100,34 | 0,70 | 0,34 | 385,3 |
| 2015 | 39104 | 425 | 153 | 101,10 | 100,39 | 1,10 | 0,39 | 392,3 |
| 2016 | 39209 | 530 | 105 | 101,37 | 100,27 | 1,37 | 0,27 | 388,9 |
| 2017 | 39311 | 632 | 102 | 101,63 | 100,26 | 1,63 | 0,26 | 392,3 |
| ∑ | 234074 | - | 632 | - | - | - | - | - |
| В среднем | 39012 | - | 126 | - | 101 | - | 1 | 126 |
Средние показатели динамики.
1. Средний уровень динамического ряда (для интервального ряда с равностоящими уровнями):
= Σ уi / n = 234074/6 = 39012 чел.2. Средний абсолютный прирост:
= Σ∆уiц / n-1 = 632/5 = 126 чел.3. Средний темп роста:
==
*100 = 100,81=101%4. Средний темп прироста:
= 101% - 100% = 1%5. Среднее абсолютное значение 1% прироста:
= 126/1 = 126 чел.Вывод: За анализируемый период численность населения ЦФО выросла на 632 человека. В среднем за месяц темп роста численности населения ЦФО составил 101% или в абсолютном выражении 126 человек, что определило его средний прирост в размере 1% в год.
Применим метод аналитического выравнивания. Выравнивание происходит по методу наименьших квадратов.
В зависимости от года t численности населения ЦФО изменяется по закону:
Yt =
+ *t, где , – параметры уравнения регрессии.Найдем параметры уравнения регрессии, решив систему уравнений, составленную по методу наименьших квадратов:
= = = = 38564.3
=
= = = 128.6Промежуточные значения расчетов приведены в таблице 7.
Таблица 7
Аналитическое выравнивание
| Год | Кол-во человек (y) | Номер периода (t) | Расчетные величины | ||
| y*t | t² |  + *t | |||
| 2012 | 38679 | 1 | 38679 | 1 | 38692,9 |
| 2013 | 38820 | 2 | 77640 | 4 | 38821,5 |
| 2014 | 38951 | 3 | 116853 | 9 | 38950,1 |
| 2015 | 39104 | 4 | 156416 | 16 | 39078,7 |
| 2016 | 39209 | 5 | 196045 | 25 | 39207,3 |
| 2017 | 39311 | 6 | 235866 | 36 | 39335,9 |
| ИТОГО | 234074 | 21 | 821499 | 91 | 234086 |