Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

Высшего образования

Уфимский государственный нефтяной технический университет

ФГБОУ ВО УГНТУ в г. Стерлитамак

Кафедра ОНХЗ

Контрольная работа №1

По дисциплине: «Теоретическая и прикладная механика»

Вариант №85

Выполнил: студент гр.БМЗз-21 -31 Евич В.С.

Проверил : Ст. преподаватель Шулаева Т.В.

Стерлитамак 2022





Задача C1 (вариант 85)

Однородная прямоугольная плита весом Р=5 кН со сторонами АВ=3а, ВС=2а, закреплена в точках А, В, С. На плиту действует момент М= 5 кН м в плоскости плиты. а=0,5 м.

Определить реакции связей в точках А, В, С.

Дано: F₂=8 кН приложена в т.Д, ₂=60, F₃=10 кН приложена в т.Н, ₃=0.

Схема №8



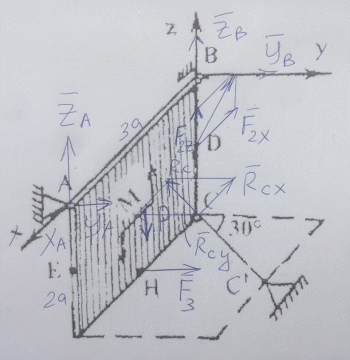
Решение.

Составим шесть уравнений равновесия





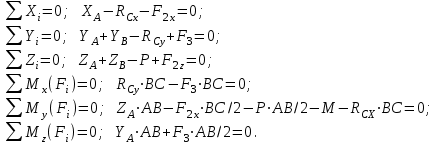
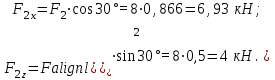
Из уравнения 6:

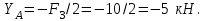
Из уравнения 4:

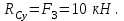
Находим реакцию в опоре С:





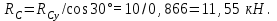
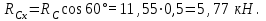
Из уравнения 2:

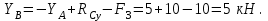
Из уравнения 1:

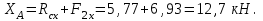
Из уравнения 5:

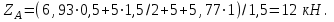
Из уравнения 3:

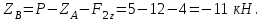
Находим реакцию в опоре А по теореме Пифагора:



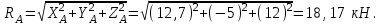
Находим реакцию в опоре В по теореме Пифагора:



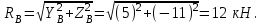
Ответ: R_A

---

=18,17 кН; R_B=12 кН; R_C=11,55 кН.

Задача К1 (вар. 85)

Дано: Тело В движется в плоскости ХY. Закон движения задан уравнениями:

y= –4 cos (t/3);

x=3 sin (t/6);

Найти: 1) уравнение траектории;

2) скорость и ускорение, касательное и нормальное ускорения и радиус кривизны при t=1 с.

Решение:

1) Выразим y через х.

cos (t/3)=1 – 2 sin² (t/6).

sin (t/6) = х / 3;

y= –4 (1 – 2 sin² (t/6)) = –4 (1 – (х / 3)²)= –4 + 4x²/9.

Это уравнение траектории тела В – парабола.
2) Скорость точки найдем по ее проекциям на координатные оси:



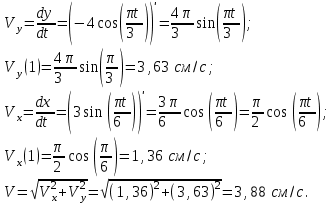
Аналогично ускорение точки найдем по ее проекциям на координатные оси:



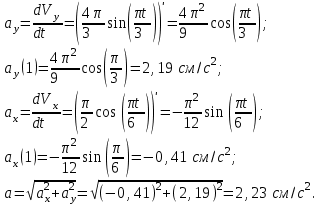
Касательное ускорение найдем, дифференцируя по времени равенство:



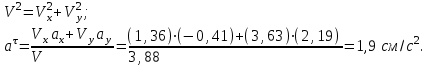
Нормальное ускорение:



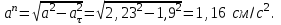
Радиус кривизны траектории:



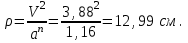
Задача К2 (вар. 85)

Плоский механизм состоит из стержней, соединенных между собой и с неподвижными опорами цилиндрическими шарнирами.

Дано: l₁=0,4 м; l₂=1,2 м; l₃=1,4 м; l₄=0,6 м

=90; =120; =90; =90; =60; V_B=8 с; а_В=10 м/с².

Найти: V_D; V_Е; _DE; а_A; _АВ

Схема №8. Строим в масштабе 1:10



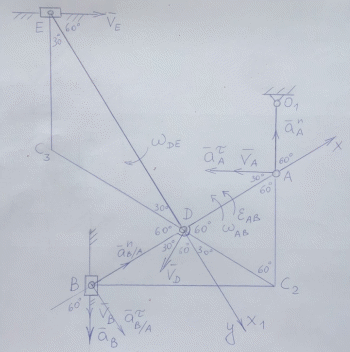
Решение

Проводим через стержень АВ ось х, находим проекции скоростей т.А и т.В

на ось х:



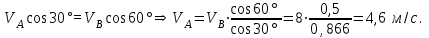
Угловая скорость стержня 1:



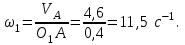
Строим мгновенный центр скоростей стержня АВ в точке пересечения перпендикуляров к скорости V_А и скорости V_В – точка С₂, соединяем ее с точкой D, находим направление скорости V_D. Скорость т.D направлена перпендикулярно DС₂.

Угловая скорость стержня АВ:



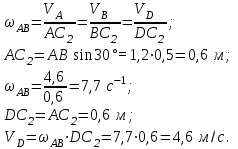
Строим мгновенный центр скоростей стержня DE в точке пересечения перпендикуляров к скорости V_D и скорости V_E – точка С₃.

Проводим через стержень DE ось х

---

₁, находим проекции скоростей т. D и т. Е

на ось х₁.



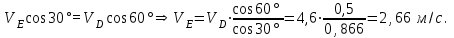
Угловая скорость стержня DE:



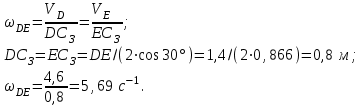
Находим ускорение точки A через сумму векторов нормального и тангенциального ускорений:



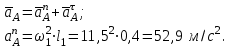
Находим ускорение точки B через сумму векторов точки A и нормального и тангенциального ускорений точки B относительно точки A:



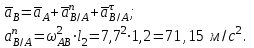
Приравниваем оба векторных уравнения:



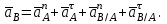
Находим проекции данных ускорений на ось х:



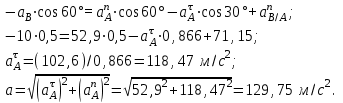
Находим проекции данных ускорений на ось у:


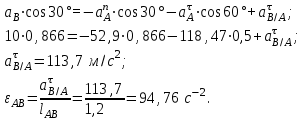
Ответ: V_D=4,6 м/с; V_Е=2,66 м/с; _DЕ=5,69 с^-1; а_А=129,75 м/с²; _АВ=94,76 с^-2.
Задача Д1 (вар. 85)

Тело массой m движется поступательно по траектории АВС, расположенной в вертикальной плоскости. Участки траектории АВ и ВС прямолинейны.

В точке А тело имеет начальную скорость V₀. Кроме того задана длина участка АВ l.

На указанных участках на тело действуют различные системы сил: кроме силы тяжести и реакции опоры на участке АВ действует постоянная сила Q и зависящая от скорости тела сила сопротивления R, на участке ВС – сила трения скольжения F_тр и переменная по времени F. Коэффициент трения скольжения f=0,1.

Требуется определить закон движения тела на участке ВС: х=f(t).

Схема 8.

Дано: m=4,5 кг; V₀=22 м/с; Q=9 Н; R=0,5V; t₁=3 c; F=3t.


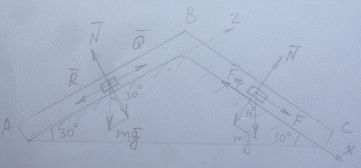
Решение

Рассмотрим участок АВ

;

;

;

;

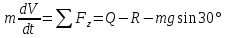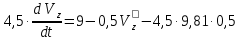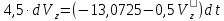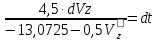пусть u= –13,0725–0,5V_z,

тогда du= –0,5 dV_z;

;

;

;

---

;

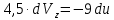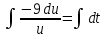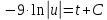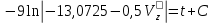
На участке АВ при z=0 V₀=22 м/с;

;

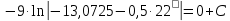С=–9 ln24,0725.

Окончательно получаем зависимость скорости на участке АВ от времени t:

;

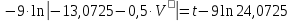Определим скорость груза в точке В при t=3 c:

;

;

;

;
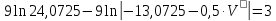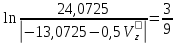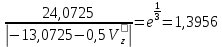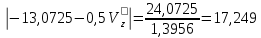–13,0725–0,5 V_z=17,249; V_z = –60,643; этот корень не удовлетворяет условию задачи;

–13,0725 – 0,5 V_z= –17,249; V_z =8,353 м/с.

Окончательно скорость в точке В принимаем V_z=8,353 м/с. Эта скорость является конечной для участка АВ и начальной для участка ВС.

Теперь рассмотрим участок ВС:



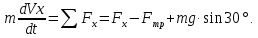
Для определения F_тр спроецируем дифференциальное уравнение движения тела на ось у:

;

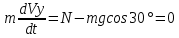т.к. V_y=0, то

N= mg cos30 =4,59,81∙0,866=38,23 H.

Сила трения F_тр=f N=0,138,23=3,823 H.

;

;

;

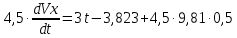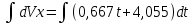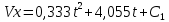Т.к. при t=0 V_x=8,353 м/с, то

8,353= 0 + 0 + C₁;

C₁=8,353;

;

;

;

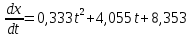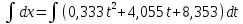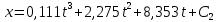Т.к. при t=0 x=0, то

0= 0 +0+0+C₂.

C₂= 0.

Окончательно получаем уравнение движения тела на участке ВС:



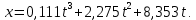
Задача Д2. (вар. 85)
Механическая система состоит из груза 1 массой m₁, ступенчатого шкива 2 массой m₂ с радиусами R₂ и r₂ и радиуса инерции ₂, шкива 3 с радиусом R₃ и распределенной по ободу массой m₃ и сплошного катка 4 массой m₄. Тела соединены нитью. К одному из тел присоединена пружина с жесткостью С. При движении на шкив 2 действует момент сопротивления М_с, на тело 1 – сила трения F_тр. Коэффициент трения f=0,1.

Система из состояния покоя приходит в движение под действием силы F=f(t), приложенной к грузу 1.

---

Найти скорость тела 1.

Дано: m₁=6 кг; m₂=5 кг; m₃=4 кг; m₄=4 кг; С=200 Н/м; М_c=1,6 Н∙м;

F=f(s₀)= 50(7+8S); R₂=0,3 м; r₂=0,1 м; ₂=0,2 м; R₃=0,2 м; S₁=0,1 м

бьтСхема 8.



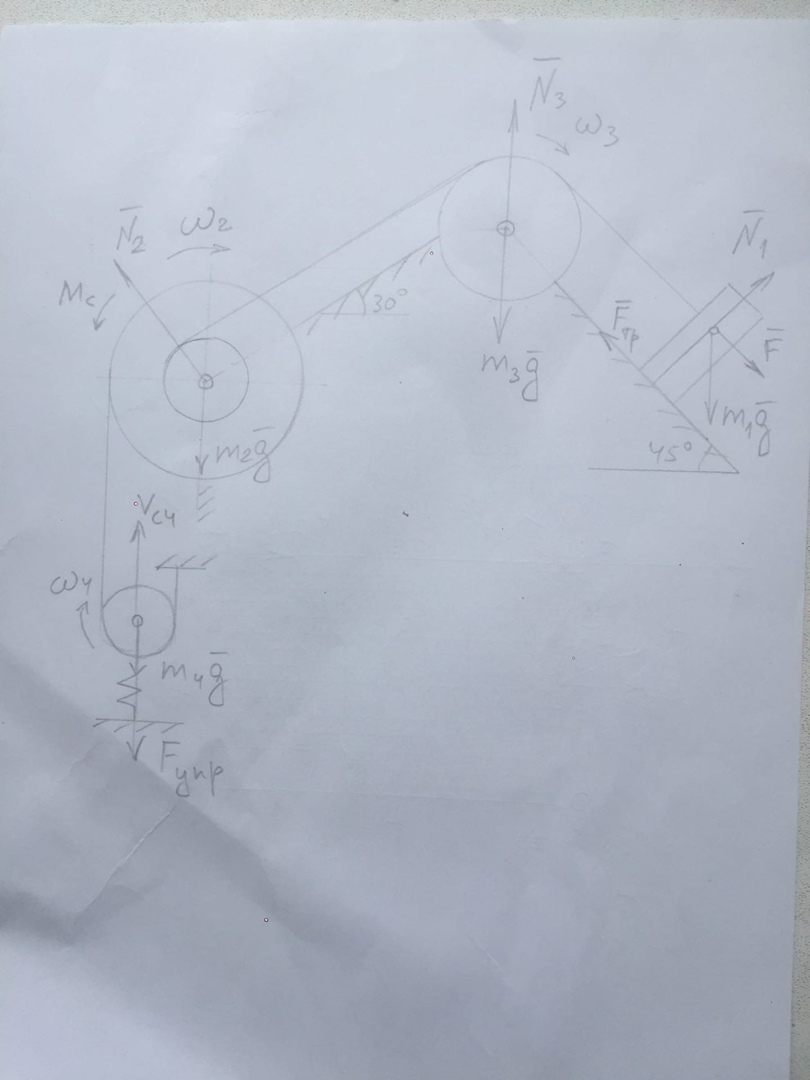
Решение

Теорема об изменении кинетической энергии системы:



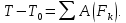
Т.к. система в начальный момент находилась в покое Т₀=0, то

Т=Т₁+Т₂+Т₃+T₄,

Тело 1 движется поступательно, его кинетическая энергия:



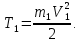
Тело 2 движется вращательно, его кинетическая энергия:



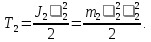
Тело 3 движется вращательно, его кинетическая энергия:



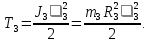
Тело 4 движется плоскопараллельно, его кинетическая энергия:



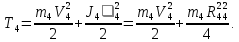
Выразим скорости тел через искомую V₁:



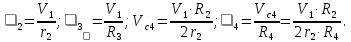
С учетом найденных соотношений:



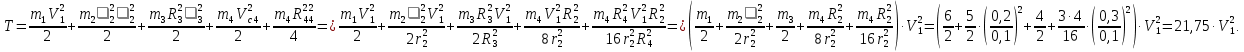
Вычислим работу внешних сил. Предварительно выразим перемещения тел через заданное S₁. Учтем, что соотношения между перемещениями тел такие же, как между соответствующими скоростями.















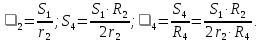
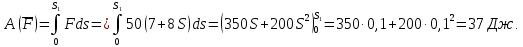
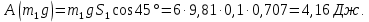
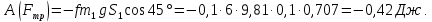
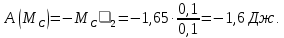
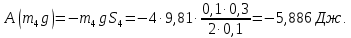
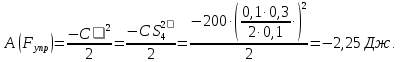
Сила N₁ направлена перпендикулярно перемещению, поэтому работы не совершает. Точки приложения сил m

---

Смотрите также файлы

• азастан республикасы білім жне ылым министрлігі с. Сейфуллин атындаы аза Агротехникалы университеті.docx

• Реферат методы определения пористости твердых тел Руководитель Половов И. Б. подпись.docx

• Самостоятельная работа Вариант 1 (10 минут).docx

• Описание возможного союзамежду Вамии человеком, родившимся.pdf

• 3. Найдите выражение для спектральной плотности сигнала (п. 2) и постройте график модуля этой спектральной плотности.docx