Файл: Методические рекомендации по выполнению контрольной работы по дисциплине Макроэкономическое планирование и прогнозирование.docx
Добавлен: 12.01.2024
Просмотров: 266
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Приложение 6
к рабочей программе
Федеральное государственное бюджетное образовательное учреждение высшего образования
УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ
УТВЕРЖДЕНЫ
на заседании кафедры региональной, муниципальной экономики и управления
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ
КОНТРОЛЬНОЙ РАБОТЫ
по дисциплине
Макроэкономическое планирование и прогнозирование
Каждому студенту необходимо решить задачи из двух контрольных работ (контрольная работа №1, контрольная работа №2). Номер варианта зависит от первой буквы в фамилии студента:
| Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Первая буква фамилии студента | А, Б, | В, Г, Д, | Е, Ё, Ж, З | И, Й, К | Л, М, Н | О, П, Р | С, Т | У, Ф, Х | Ц, Ч, Ш, Щ | Э, Ю, Я |
Замена одного варианта другим возможна только в исключительных случаях с разрешения кафедры.
Указания по выполнению работ
1. Разработка прогнозов с помощью метода скользящей средней
Одним из наиболее старых и широко известных методов сглаживания временных рядов является метод скользящих средних. Применяя этот метод, можно элиминировать случайные колебания и получить значения, соответствующие влиянию главных факторов. Сглаживание с помощью скользящих средних основано на том, что в средних величинах взаимно погашаются случайные отклонения. Это происходит вследствие замены первоначальных уровней временного ряда средней арифметической величиной внутри выбранного интервала времени. Полученное значение относится к середине выбранного периода. Затем период сдвигается на одно наблюдение, и расчет средней повторяется, причем периоды определения средней берутся все время одинаковыми. Таким образом, в каждом случае средняя центрирована, т.е. отнесена к серединной точке интервала сглаживания и представляет собой уровень для этой точки.
При сглаживании временного ряда скользящими средними в расчетах участвуют все уровни ряда. Чем шире интервал сгаживания, тем более плавным получается тренд. Сглаженный ряд короче первоначального на (n–1) наблюдений (n – величина интервала сглаживания). При больших значениях n колеблемость сглаженного ряда значительно снижается. Одновременно заметно сокращается количество наблюдений, что создает трудности.
Выбор интервала сглаживания зависит от целей исследования. При этом следует руководствоваться тем, в какой период времени происходит действие, а следовательно, и устранение влияния случайных факторов.
Данный метод используется при краткосрочном прогнозировании. Его рабочая формула:
= 
+ 
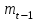, (1)гдеt + 1 – прогнозный период;
t – период, предшествующий прогнозному периоду (год, месяц и т.д.);
yt+1 – прогнозируемый показатель;
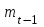– скользящая средняя за два периода до прогнозного; n – число уровней, входящих в интервал сглаживания;
yt– фактическое значение исследуемого явления за предшествующий период;
yt-1 – фактическое значение исследуемого явления за два периода, предшествующих прогнозному.
2. Прогнозирование на основе метода
экспоненциального сглаживания
Этот метод наиболее эффективен при разработке среднесрочных прогнозов. Он приемлем при прогнозировании только на один период вперед. Его основные достоинства:
простота процедура вычислений;
возможность учета весов исходной информации.
Рабочая формула метода экспоненциального сглаживания:
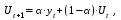(2)где t – период, предшествующий прогнозному;
t+1– прогнозный период;
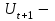
прогнозируемый показатель;
параметр сглаживания;
фактическое значение исследуемого показателя за период, предшествующий прогнозному;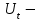 
экспоненциально взвешенная средняя для периода, предшествующего прогнозному.При прогнозировании данным методом возникает два затруднения:
1) выбор значения параметра сглаживания
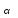;2) определение начального значения U1.
От величины α будет зависеть, как быстро снижается вес влияния предшествующих наблюдений. Чем больше α, тем меньше сказывается влияние предшествующих лет. Если значение α близко к единице, то это приводит к учету при прогнозе в основном влияния лишь последних наблюдений; если близко к нулю, то веса, по которым взвешиваются уровни временного ряда, убывают медленно, т.е. при прогнозе учитываются все (или почти все) прошлые наблюдения. Таким образом, если есть уверенность, что начальные условия, на основании которых разрабатывается прогноз, достоверны, следует использовать небольшую величину параметра сглаживания (α→0). Когда параметр сглаживания мал, то исследуемая функция ведет себя как средняя из большого числа прошлых уровней. Если нет достаточной уверенности в начальных условиях прогнозирования, то следует использовать большую величину α, что приведет к учету при прогнозе в основном влияния последних наблюдений.
Точного метода для выбора оптимальной величины параметра сглаживания α нет. В отдельных случаях автор данного метода профессор Браун предлагал определять величину α, исходя из длины интервала сглаживания. При этом α вычисляется по формуле
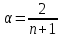, (3)где n– число наблюдений, входящих в интервал сглаживания.
Задача выбора U1 (экспоненциально взвешенного среднего начального) решается следующими путями:
1) если есть данные о развитии явления в прошлом, то можно воспользоваться средней арифметической, и U1 равен этой средней арифметической;
2) если таких сведений нет, то в качестве
U1 используют исходное первое значение базы прогноза Y1.
Также можно воспользоваться экспертными оценками.
Метод экспоненциального сглаживания нередко не «срабатывает» при изучении экономических временных рядов и прогнозировании экономических процессов. Это обусловлено тем, что экономические временные ряды бывают слишком короткими (15-20 наблюдений), и в случае, когда темпы роста и прироста велики, данный метод не «успевает» отразить все изменения.
3. Разработка прогнозов методом наименьших квадратов
Сущность метода состоит в минимизации суммы квадратических отклонений между наблюдаемыми и расчетными величинами. Расчетные величины находятся по подобранному уравнению – уравнению регрессии.
Чем меньше расстояние между фактическими значениями и расчетными, тем более точен прогноз, построенный на основе уравнения регрессии. Теоретический анализ сущности изучаемого явления, изменение которого отображается временным рядом, служит основой для выбора кривой. Иногда принимаются во внимание соображения о характере роста уровней ряда. Так, если рост выпуска продукции ожидается в арифметической прогрессии, то сглаживание производится по прямой. Если же оказывается, что рост идет в геометрической прогрессии, то сглаживание надо производить по показательной функции.
Рабочая формула метода наименьших квадратов:
у t+1 = а*Х + b, (4)
гдеt + 1 – прогнозный период;
yt+1 – прогнозируемый показатель;
a и b- коэффициенты;
Х - условное обозначение времени.
Расчет коэффициентов a иbосуществляется по следующим формулам:
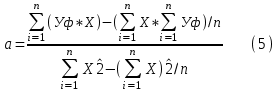
где, Уф – фактические значения ряда динамики;
n– число уровней временного ряда;
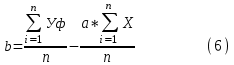
С
глаживание временных рядов методом наименьших квадратов служит для отражения закономерности развития изучаемого явления. В аналитическом выражении тренда время рассматривается как независимая переменная, а уровни ряда выступают как функция этой независимой переменной. Ясно, что развитие явления зависит не от того, сколько лет прошло с отправного момента, а от того, какие факторы влияли на его развитие, в каком направлении и с какой интенсивностью. Развитие явления во времени выступает как результат действия этих факторов.
Правильно установить тип кривой, тип аналитической зависимости от времени – одна из самых трудных задач предпрогнозного анализа.
Подбор вида функции, описывающей тренд, параметры которой определяются методом наименьших квадратов, производится в большинстве случаев эмпирически, путем построения ряда функций и сравнения их между собой по величине среднеквадратической ошибки, вычисляемой по формуле
S = 
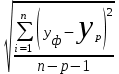, (7)где yф – фактические значения ряда динамики;
yр – расчетные (сглаженные) значения ряда динамики;
n– число уровней временного ряда;
р – число параметров, определяемых в формулах, описывающих тренд.
Недостатки метода наименьших квадратов:
1) изучаемое экономическое явление мы пытаемся описать с помощью математического уравнения, поэтому прогноз будет точен для небольшого периода времени, и уравнение регрессии следует пересчитывать по мере поступления новой информации;
2) сложность подбора уравнения регрессии. Эта проблема разрешима при использовании типовых компьютерных программ.
4. Оценка точности прогнозов, построенных методами
экстраполяции
Точность прогноза – это важнейшая его характеристика. Существует несколько способов оценки точности прогнозов:
1) средняя абсолютная оценка:
Δ
, (8)где n – число уровней временного ряда;
2) средняя квадратическая оценка:
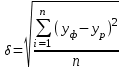. (9)Чем ближе к нулю первый и второй показатели, тем выше точность прогноза;
3) средняя относительная ошибка:
ε=
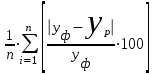(10)Интерпретация значений средней относительной ошибки для оценки точности прогнозов:
| ε, % | Интерпретация |
| < 10 | Точность прогноза высокая |
| 10-20 | Точность хорошая |
| 20-50 | Точность удовлетворительная |
| > 50 | Точность неудовлетворительная |