Файл: Контрольная работа По дисциплине Информационные технологии в корпоративных сетях.docx

(12)



(13)



(14)



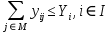
которая разрешима при условии



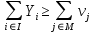
Задачи «назначения» (1)-(2), (4)-(6), (7)-(8), (9)-(11) и (12)-(14) формулировались для случая одного проекта. Аналогично ставятся и решаются задачи синтеза оптимальных (матричных и линейных) структур и для случая, когда система реализует последовательно набор проектов с заданными характеристиками (или характеристиками, относительно которых имеется статистическая информация). Матричной структуре при этом соответствуют изменяющиеся во времени (в зависимости от реализуемого проекта) распределения работ по АЭ (с этой точки зрения матричная структура управления, определяемая в результате решения задач «назначения» на каждом шаге, близка к сетевой структуре [40]), линейной – постоянное закрепление АЭ за определенными центрами (типами работ). Эффективность той или иной структуры в динамике может оцениваться как сумма (или математическое ожидание, если характеристики потока достоверно неизвестны) затрат на реализацию всего набора проектов за рассматриваемый период времени. Вывод утверждения 10 о том, что матричная структура характеризуется не большими суммарными затратами АЭ, чем линейная, в динамике также остается в силе.

Приведем пример. Пусть имеются два типа работ и два АЭ, удельные затраты которых представлены матрицей 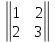, ограничения объемов работ АЭ: Y₁ = Y₂ = 1, рассматривался поток из 60 проектов объемами (v₁, v₂), которые равномерно распределены на v₁ + v₂≤ 2. Численное моделирование заключалось в нахождении для каждого проекта:

• 
  затрат c¹ (решение задачи (9)-(11)) при назначении - один из вариантов постоянной (не изменяющейся во времени) линейной структуры;
  
• 
  затрат c²(решение задачи (9)-(11)) при назначении - один из вариантов постоянной (не изменяющейся во времени) линейной структуры;
  
• 
  затрат c – оптимальное решение задачи (9)-(11) – оптимальная на каждом шаге линейная структура без ограничений на индивидуальные объемы работ АЭ;
  
• 
  затрат c⁰⁰ – оптимальное решение задачи (7)-(8) – оптимальная на каждом шаге матричная структура без ограничений на индивидуальные объемы работ АЭ;
  
• 
  затрат c⁰ – оптимальное решение задачи (12)-(14) – оптимальная на каждом шаге матричная структура c ограничениями на индивидуальные объемы работ АЭ.
  

---

Средние (по всем 60 проектам) значения затрат приведены в таблице 1.



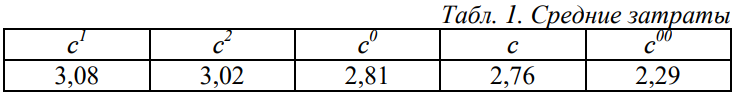
На рисунке 14 приведены графики отношений (c₁ / c – 1) и (c₁ / c – 1), характеризующий потери в эффективности из-за использования постоянной (не зависящей от специфики реализуемого проекта) линейной структуры.



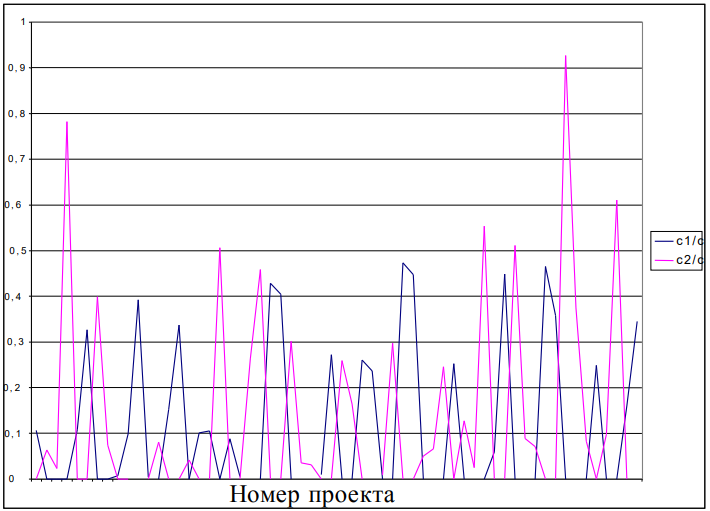
Рис. 14. Эффективность постоянной линейной структуры

На рисунке 15 приведены графики затрат c – оптимального решения задачи (9)-(11) – прерывистая линия – и c⁰⁰ – оптимального решения задачи (7)-(8) – непрерывная линия, которые позволяют оценить потери в эффективности от использования линейной структуры по сравнению с матричной (см. также утверждение 10).

Таким образом, постановка и решение задач «назначения» позволяет оценивать сравнительную эффективность различных структур и закономерностей их трансформации, осуществлять выбор оптимальной или рациональной структуры управляющей компании в зависимости от набора проектов, реализуемых в рамках корпоративной программы.

Модель распределенного контроля. Результаты анализа систем с распределенным контролем, в которых один и тот же активный элемент одновременно подчинен нескольким центрам, свидетельствуют, что существуют два режима взаимодействия центров – режим сотрудничества и режим конкуренции (см. первый раздел).



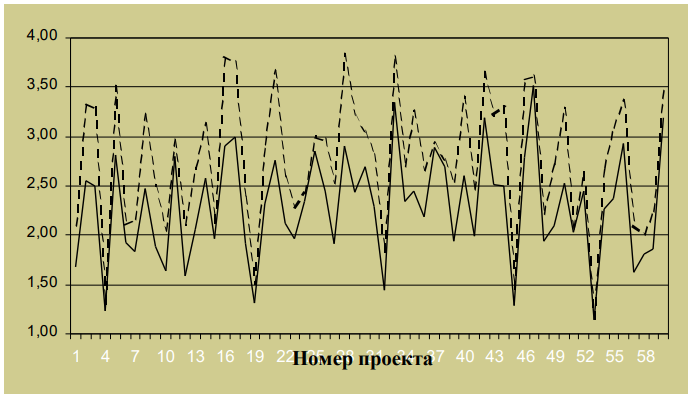
Рис. 15. Эффективности линейной и матричной структур

В режиме сотрудничества АЭ выбирает действие, выгодное (в определенном смысле) всем центрам одновременно, и центры осуществляют совместное управление данным АЭ. Такая ситуация соответствует матричной структуре управления.

В режиме конкуренции управление АЭ осуществляется одним центром, который определяется по результатам анализа аукционного равновесия игры центров. Такая ситуация соответствует линейной (веерной) структуре управления.

Условием реализации режима сотрудничества (и, следовательно, матричной структуры) является непустота области компромисса. Для непустоты области компромисса, в свою очередь, необходимо и достаточно, чтобы максимальное (по действиям АЭ) значение суммы целевых функции всех участников системы (всех центров и АЭ) было не меньше, чем сумма максимумов значений целевых функций центров, каждый из которых вычисляется в предположении, что он осуществляет единоличное управление АЭ.

---

Если целевые функции и допустимые множества участников системы зависят от некоторых параметров, то можно исследовать зависимость структуры системы от этих параметров – при тех комбинациях параметров, при которых имеет место вышеупомянутое условие следует реализовывать матричную структуру, при остальных значениях параметров – линейную структуру. Если известна стоимость изменения этих параметров, то можно ставить решать задачу развития (оптимального изменения параметров с учетом затрат на изменения и эффективности структур) по аналогии с тем, как это делается в [2].

Рассмотрим пример, иллюстрирующий применение описанного общего подхода. Рассмотрим систему, состоящую их одного АЭ и двух центров. Стратегией АЭ является выбор действия 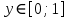, содержательно интерпретируемого как доля всего рабочего времени АЭ, отрабатываемого на первый центр. Соответственно, (1 – y) характеризует долю времени, отрабатываемого на второй центр. Центры получают доходы, зависящие от того времени, которое на них отработал АЭ: H₁(y) = y, H₂(y) = y, где 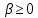- некоторый параметр. АЭ несет затраты c(y) = y² / 2 + (1 – y)² / 2.

Определим наиболее выгодное для первого центра действие АЭ (максимизирующее разность между H₁(y) и c(y)):



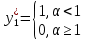
Определим наиболее выгодное для второго центра действие АЭ (максимизирующее разность между H₂(y) и c(y)):



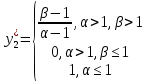
Вычисляем соответствующие значения целевых функций центров:

• 
  в области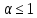 центры получают (управляя АЭ поодиночке) следующие полезности: W₁ = 1 –  / 2, W₂ =  –  /2;
  
• 
  в области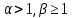 центры получают (управляя АЭ поодиночке) следующие полезности: W₁ = - 1 / 2, W₂ = [6 – (1 + ) ² – 2  – 3  + 2 ] / 2 ( – 1)²,
  
• 
  в области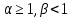 центры получают (управляя АЭ поодиночке) следующие полезности: W₁ = - 1 / 2, W₂ = - 1 / 2.
  

---

Определим действие y₀, доставляющее максимум [H₁(y) + H₂(y) – c(y)]: y₀ = min [ / (1 + ); 1], и



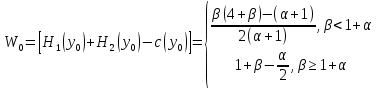
Условие непустоты области компромисса (и реализуемости матричной структуры) имеет вид:

(15)

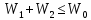
Так как каждая из величин W₁, W₂ и W₀ зависит от параметров (; ), то можно найти множество значений этих параметров, при которых условие (15) выполнено. Для рассматриваемого примера на рисунке 16 заштриховано множество значений параметров  и , при которых оптимальной является матричная структура. В незаштрихованных областях оптимальна линейная структура, причем в равновесии АЭ оказывается починенным всегда только второму центру.



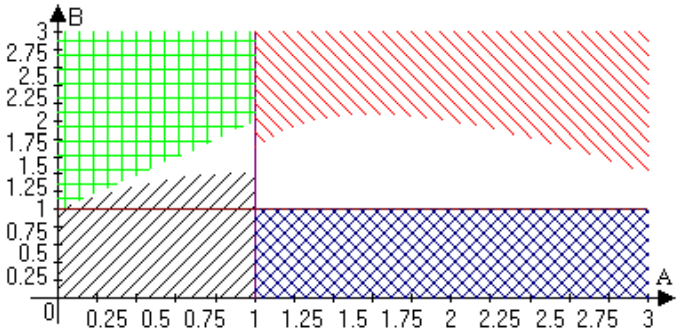
Рис. 16. Области значений параметров  и , в которых оптимальна матричная структура

Параметрический анализ, аналогичный проведенному выше, оказывается эффективным и в динамике, так как знание областей оптимальности различных структур при наличии прогноза изменений существенных параметров позволяет априори синтезировать структуру управляющей компании, обладающую максимальной (или максимальной ожидаемой, или допустимой и т.д. – в зависимости от решаемой задачи) эффективностью.

---

Разбиение на уроки.

Введение.

В настоящем разделе рассматриваются две модели формирования и оптимизации структуры управляющей компании. Первая модель основывается на решении задач «назначения» – определения распределения активных элементов по работам проектов, вторая – на результатах исследования активных систем с распределенным контролем, приведенных в первом разделе и в [23, 25, 43, 46].

Для большинства современных организаций и фирм (не только для компаний, управляющих реализацией корпоративных программ) актуальна проблема поиска рационального баланса между функциональной и проектной структурой. Линейная структура, порождаемая функциональной² специализацией, оказывается эффективной при процессном функционировании, то есть в условиях относительного постоянства набора реализуемых системой функций. При проектной структуре участники системы «привязаны» не к функциям, а к проектам, которые могут сменять друг друга во времени (см. подробное обсуждение свойств линейных, матричных и сетевых структур в [19, 40]). Гибридом функциональной и проектной структур является матричная структура, в которой каждый исполнитель в общем случае подчинен одновременно нескольким руководителям – например, некоторому функциональному руководителю и руководителю определенного проекта.

Поэтому ниже рассматриваются модели, учитывающие плюсы и минусы различных структур и позволяющие определять оптимальные (по оговариваемому в каждом конкретном случае критерию) типы структур. Отметим, что речь идет именно о типе структуры, так как задача синтеза оптимальной иерархической структуры в целом не рассматривается (см. соответствующие модели в [19, 28, 38, 40, 59]) – исследование ограничивается анализом простейших двухуровневых «блоков».

Урок 1.

Модель «назначения». Пусть в системе имеются n АЭ – исполнителей работ по корпоративным проектам (I = {1, 2, …, n} – множество АЭ) и m ≤ n центров, каждому из которых поставлен в соответствие некоторый тип работ. Тогда проект (выбираемый за единицу времени) может характеризоваться вектором v = (v₁, v₂, …, v_m) объемов работ, где v_j≥ 0, j Є M – множеству работ (центров).

Введем матрицу

---