Файл: Краевое государственное автономное профессиональное образовательное учреждение Нытвенский многопрофильный техникум.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 94
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2. Применение непрерывности.
Решить неравенства:
| |
3. Показательная и логарифмическая функции.
| Решить уравнения:
11) 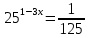 12) log3(5х – 6) - log72= 3 13) log0,5 (2х + 1) = -2 14) log2 (4-2x) + log23= l 15) log7(x-l)=log72 + log73 | Решить неравенства:
|
4. Функции: их свойства и графики.
Функция у = f(x) задана своим графиком. Укажите:
1) область определения функции;
2) область значения функции;
3) нули функции;
4) интервалы знакопостоянства функции;
5) промежутки возрастания и промежутки убывания функции;
6) точки экстремума функции;
7) наибольшее и наименьшее значения функции.
| 1. 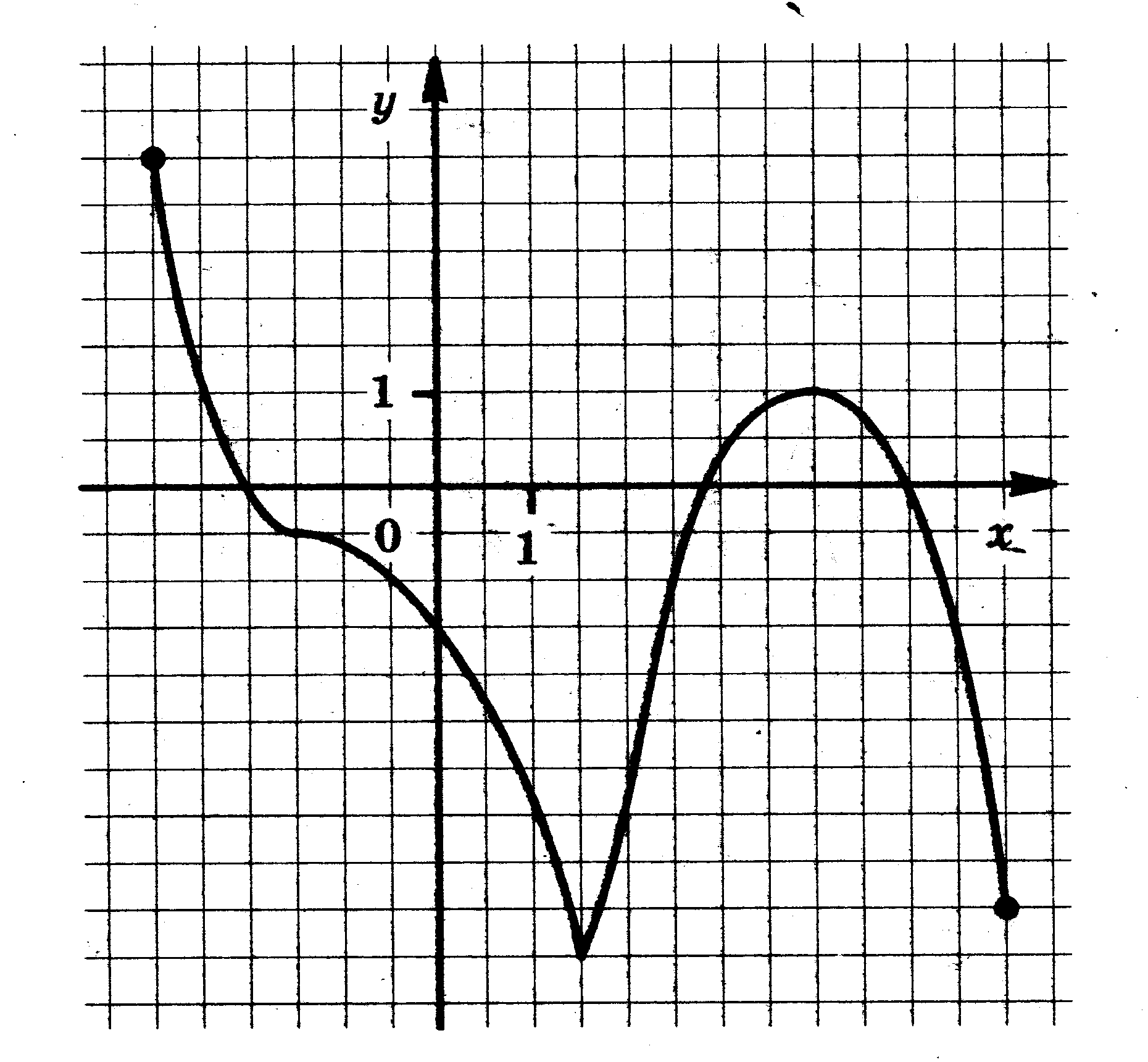 | 2. 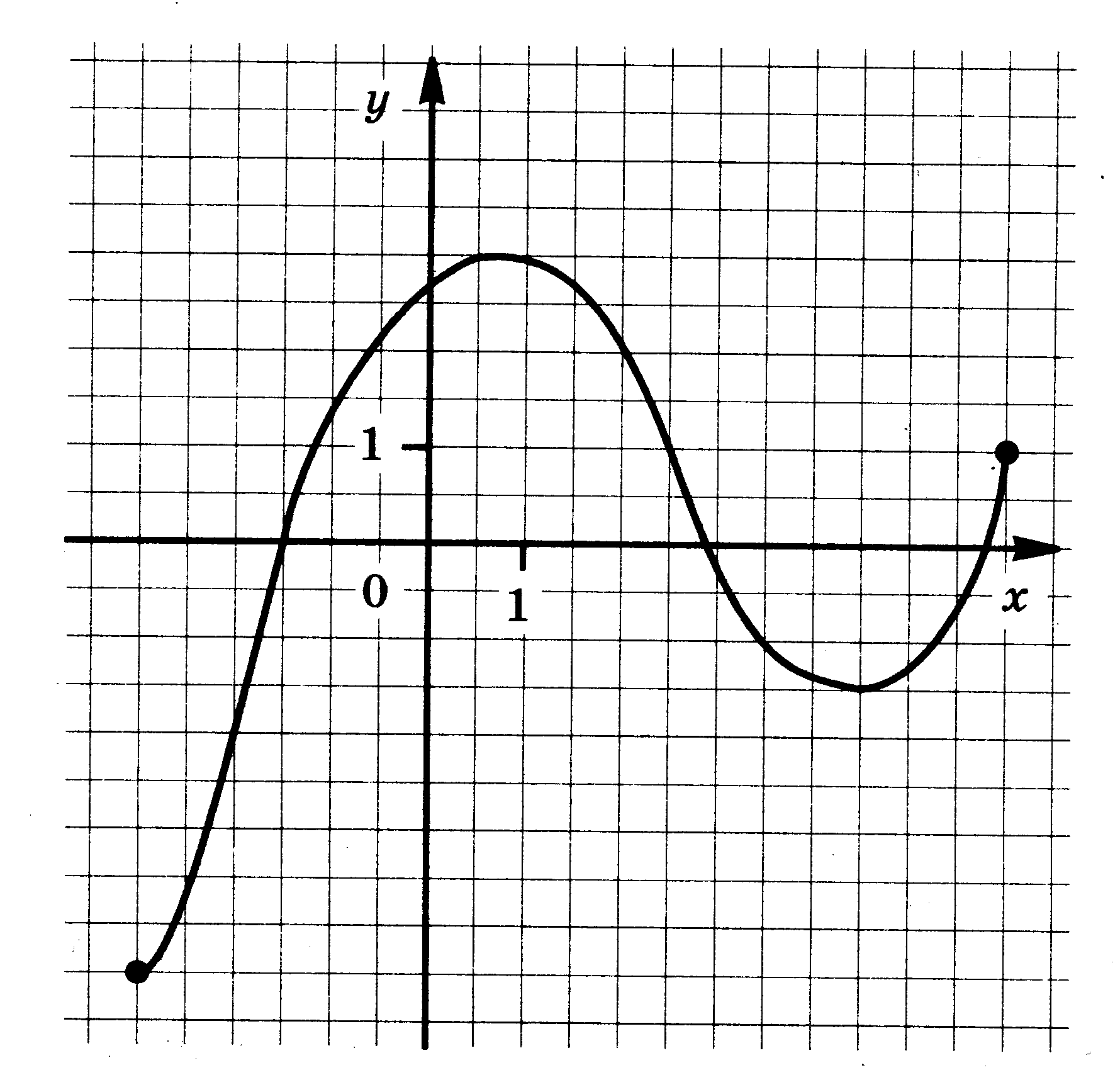 |
| 3. 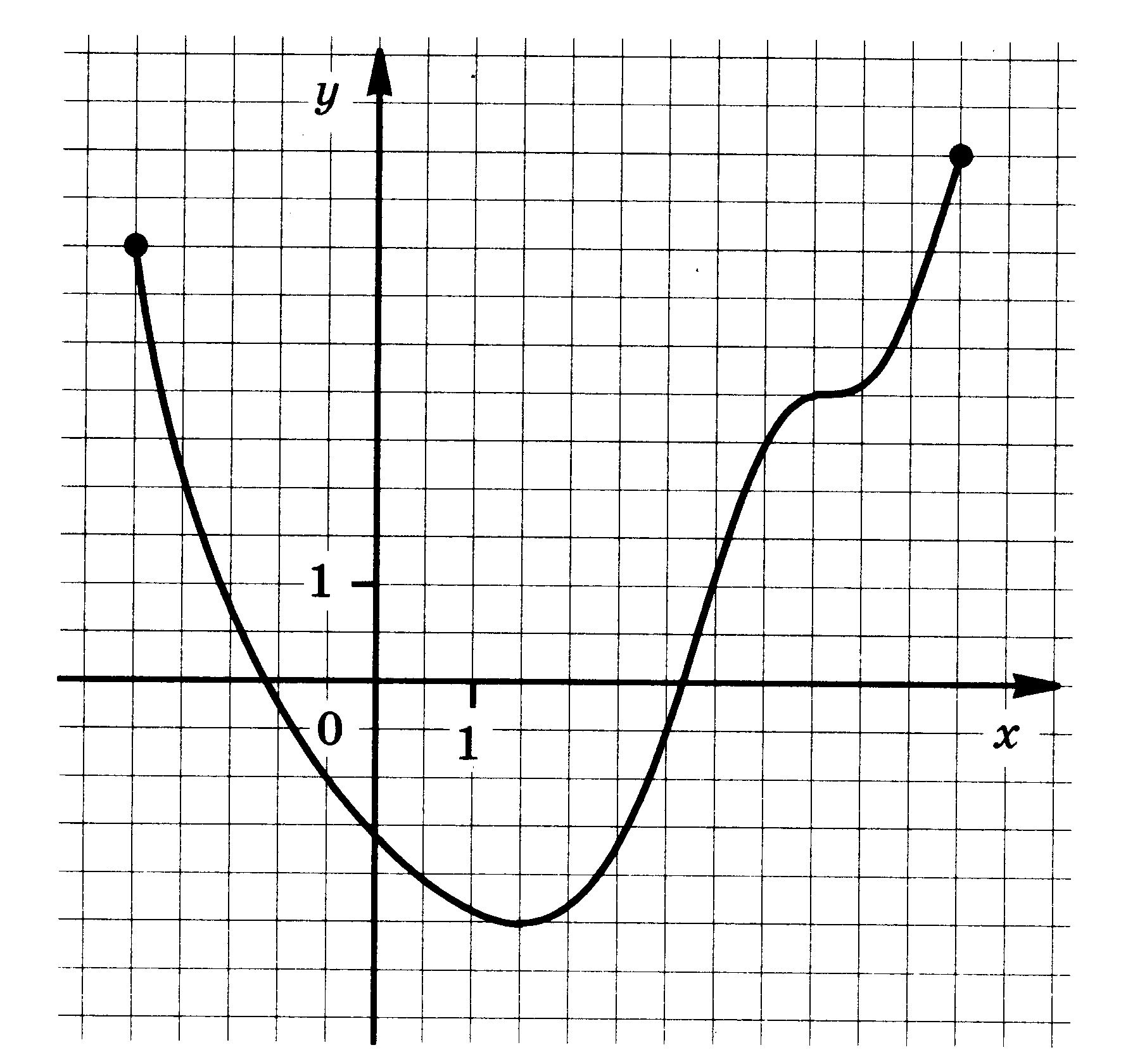 | 4. 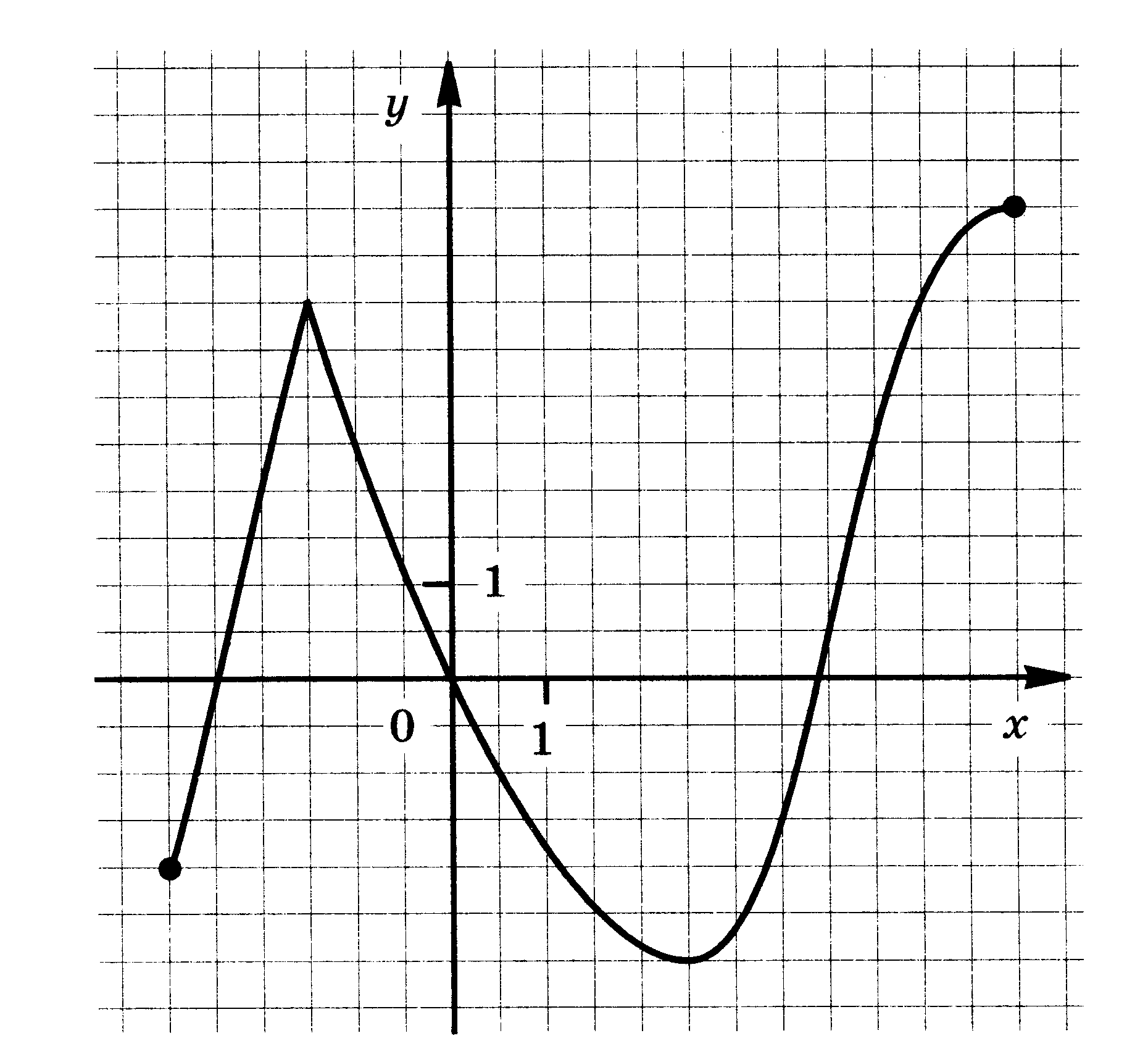 |
| 5. 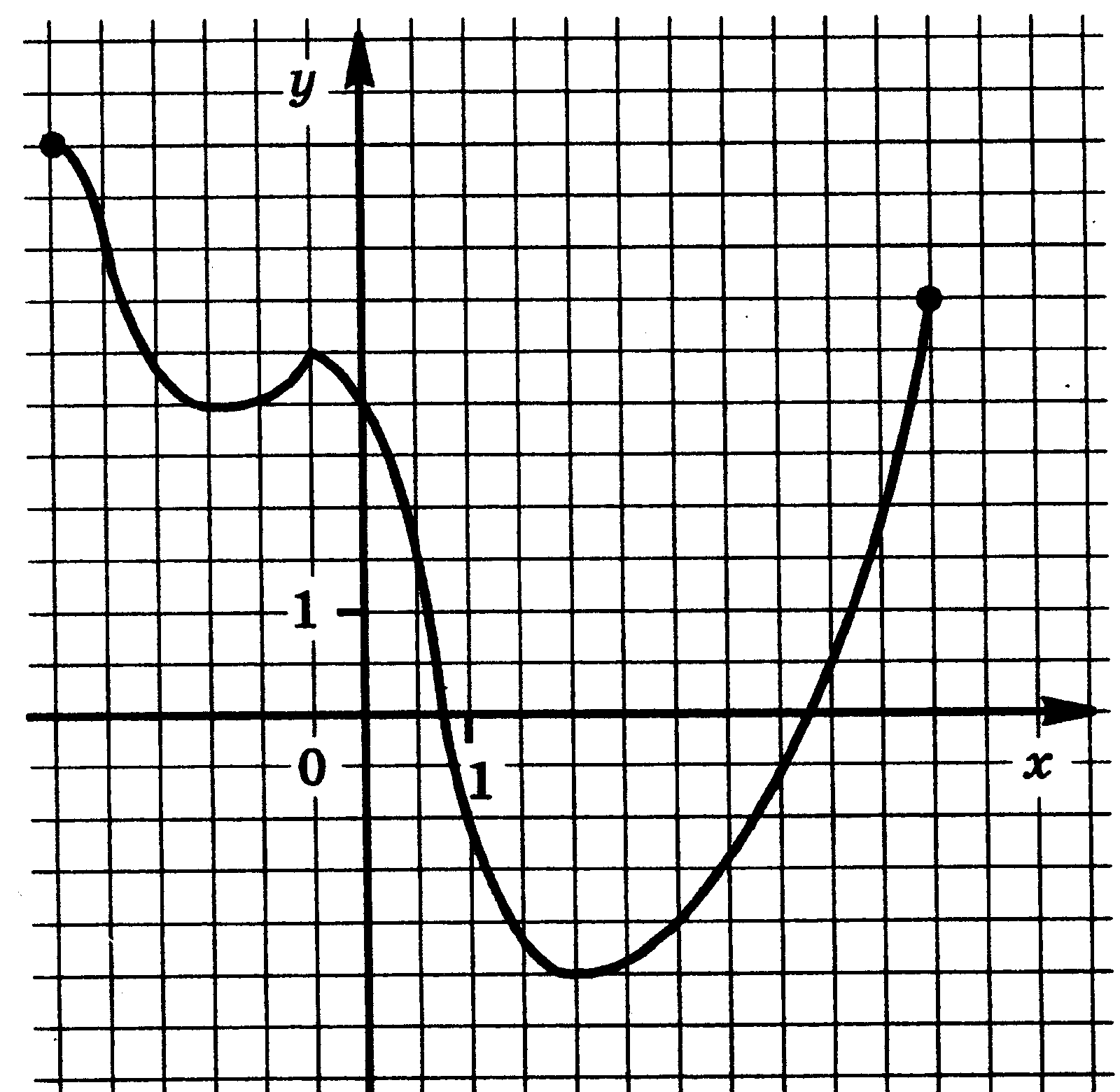 | 6. 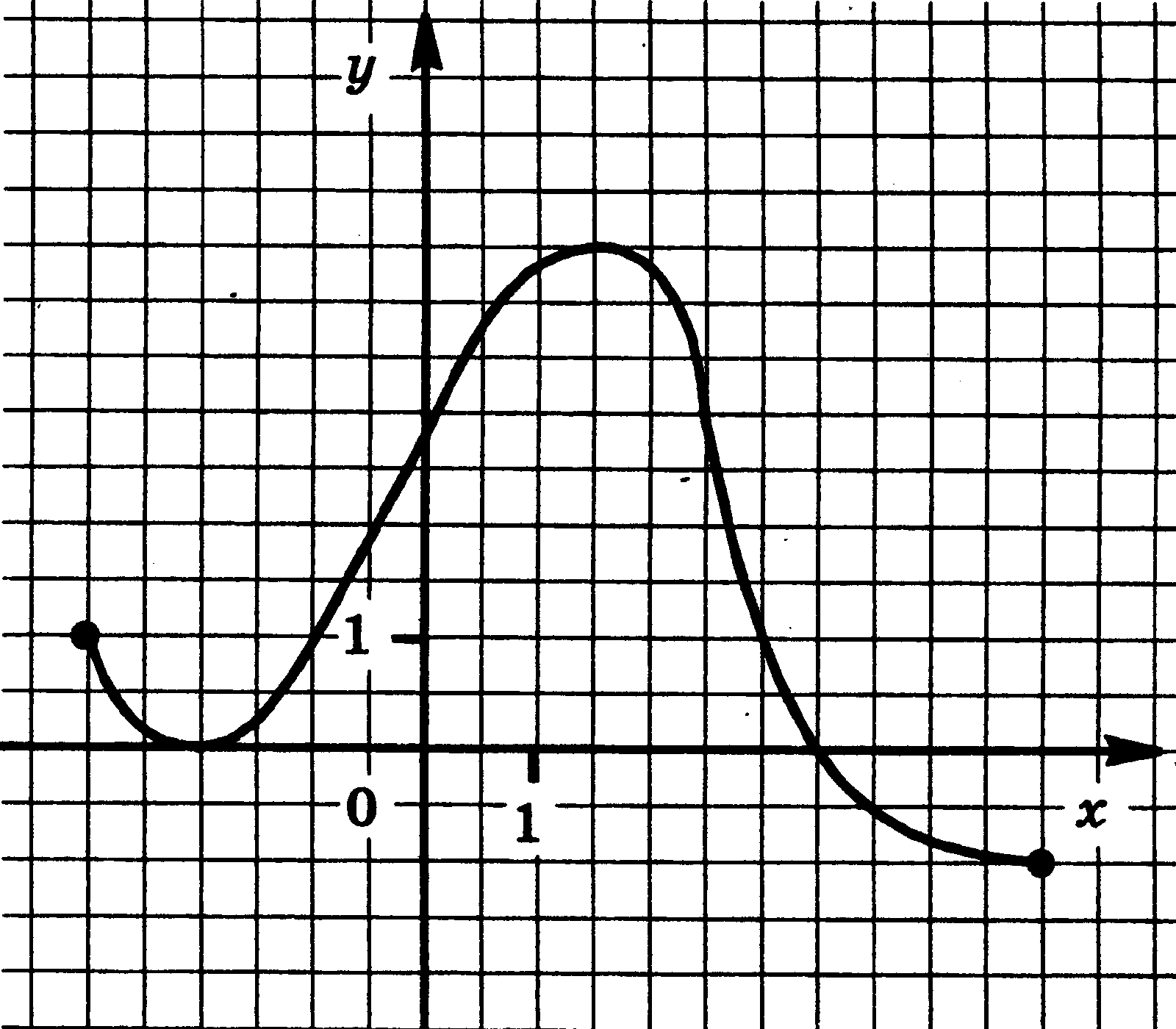 |
| 7. 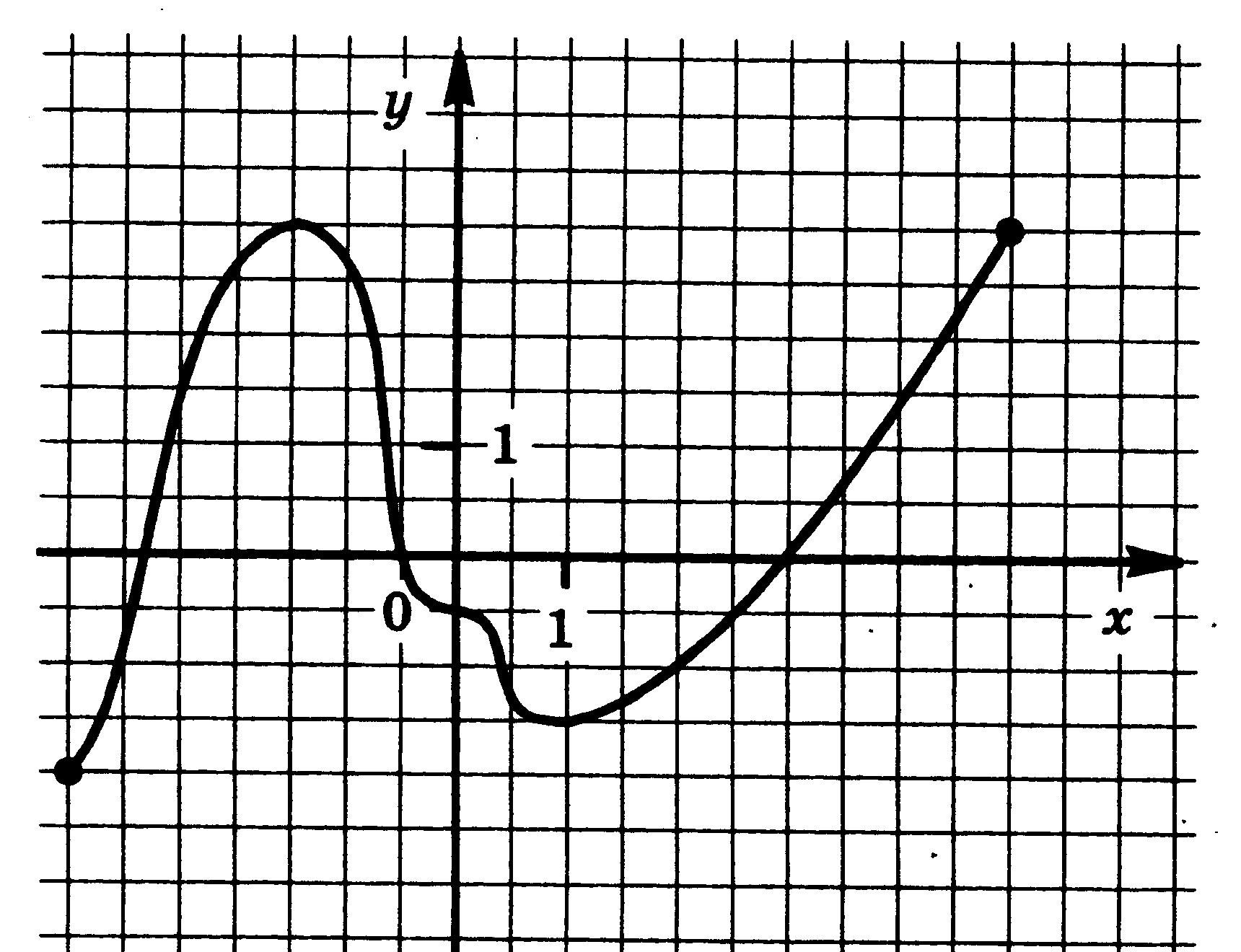 | 8. 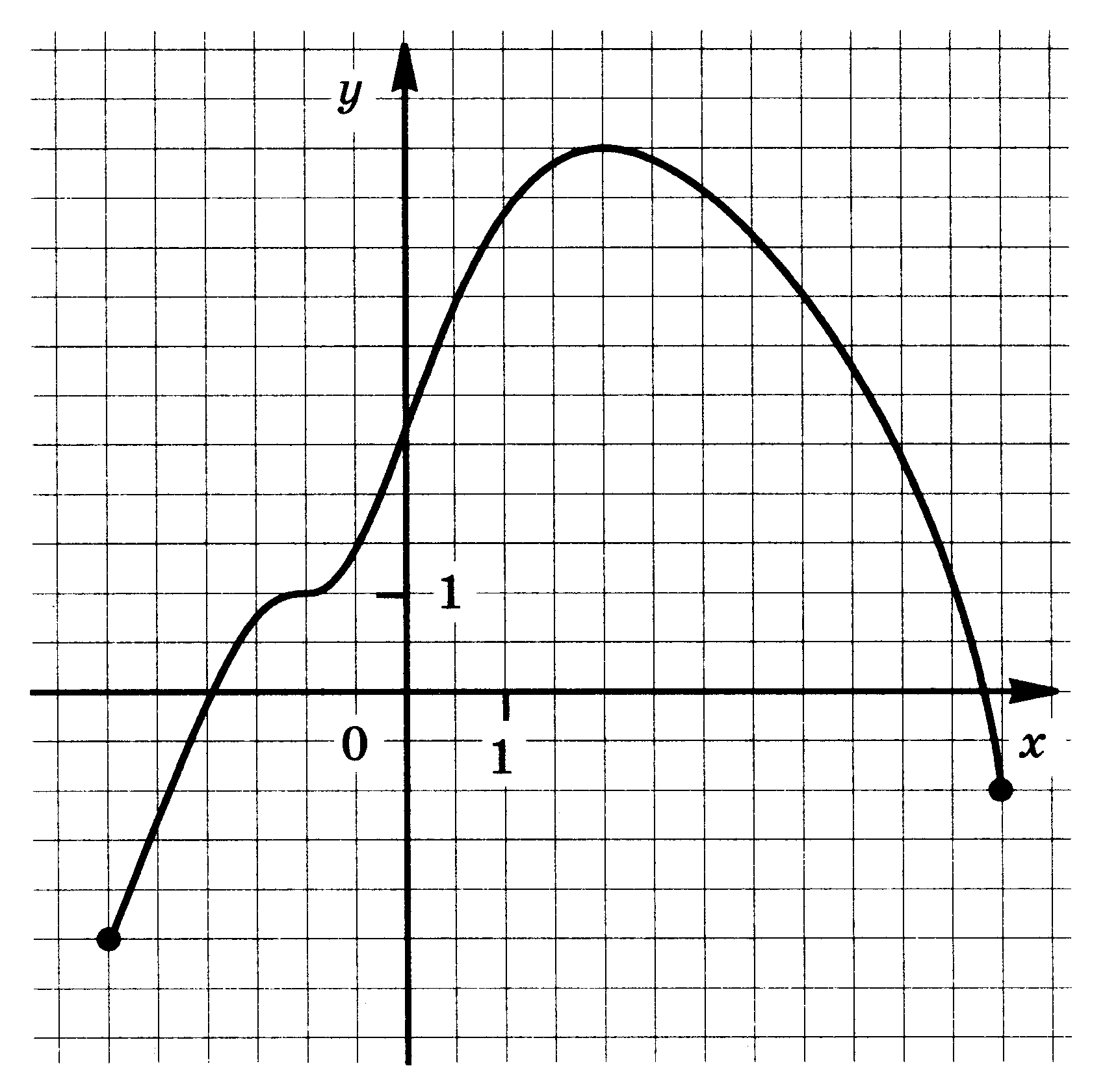 |
| 9. 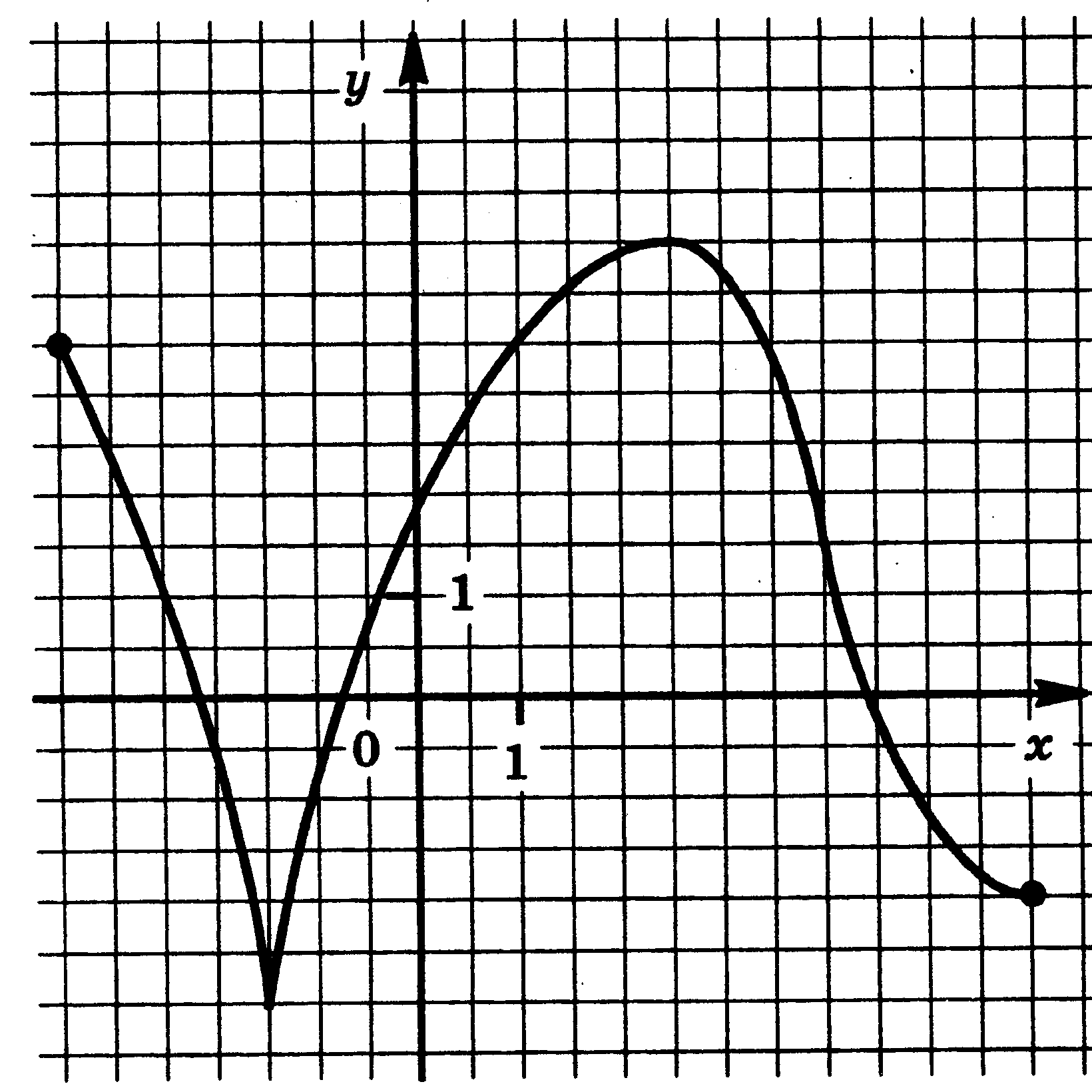 | 10. 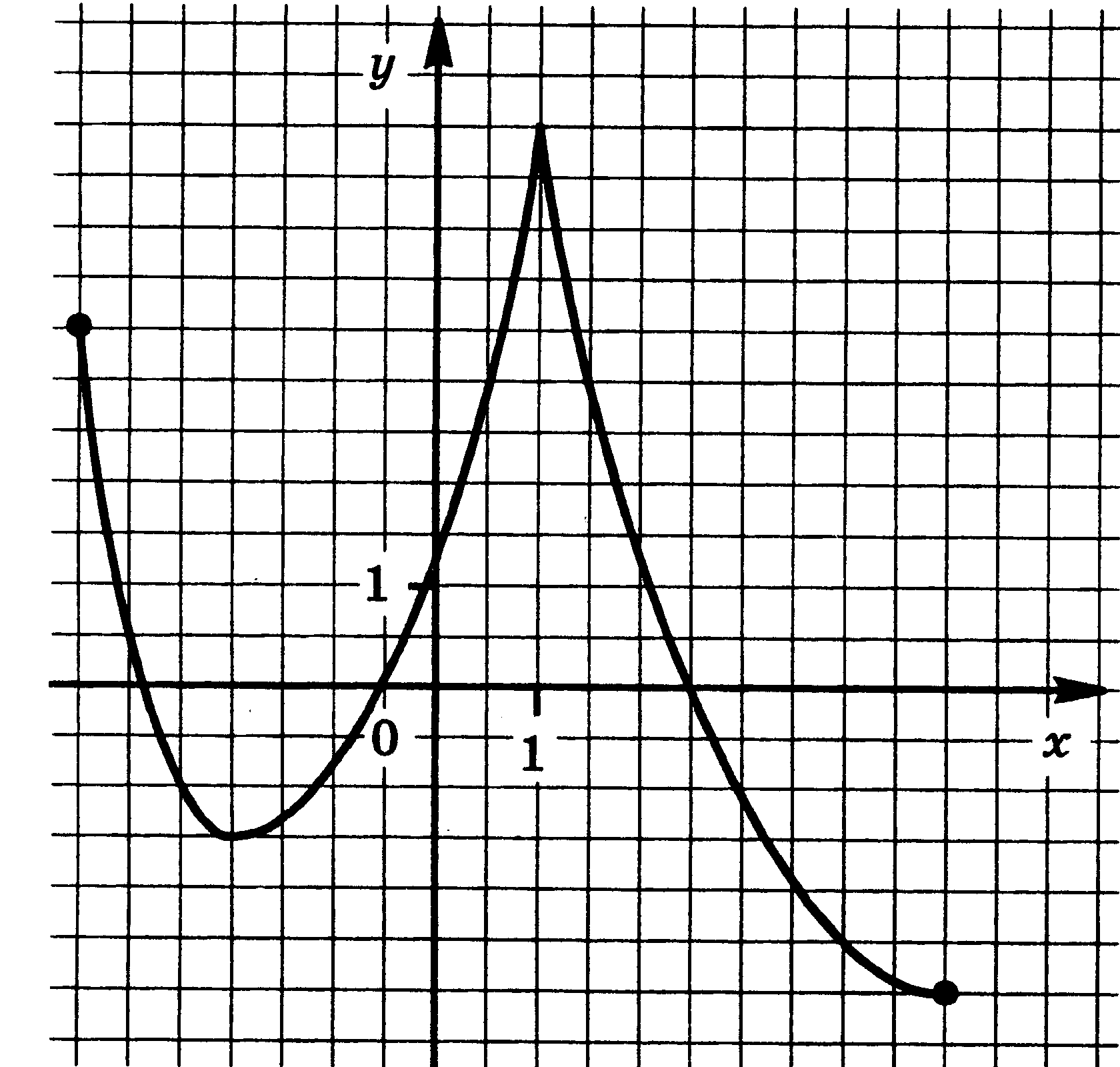 |
| 11. 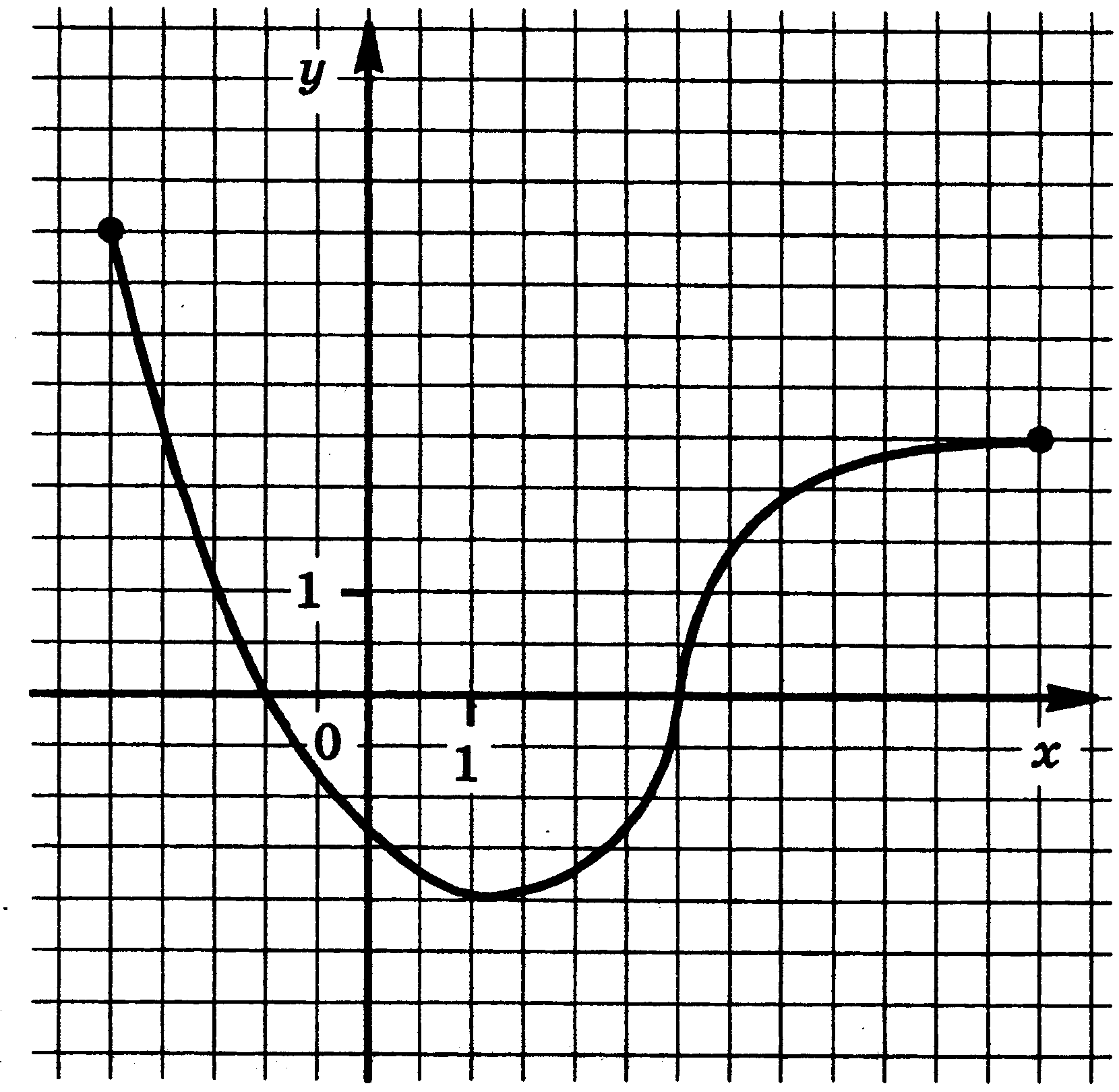 | 12. 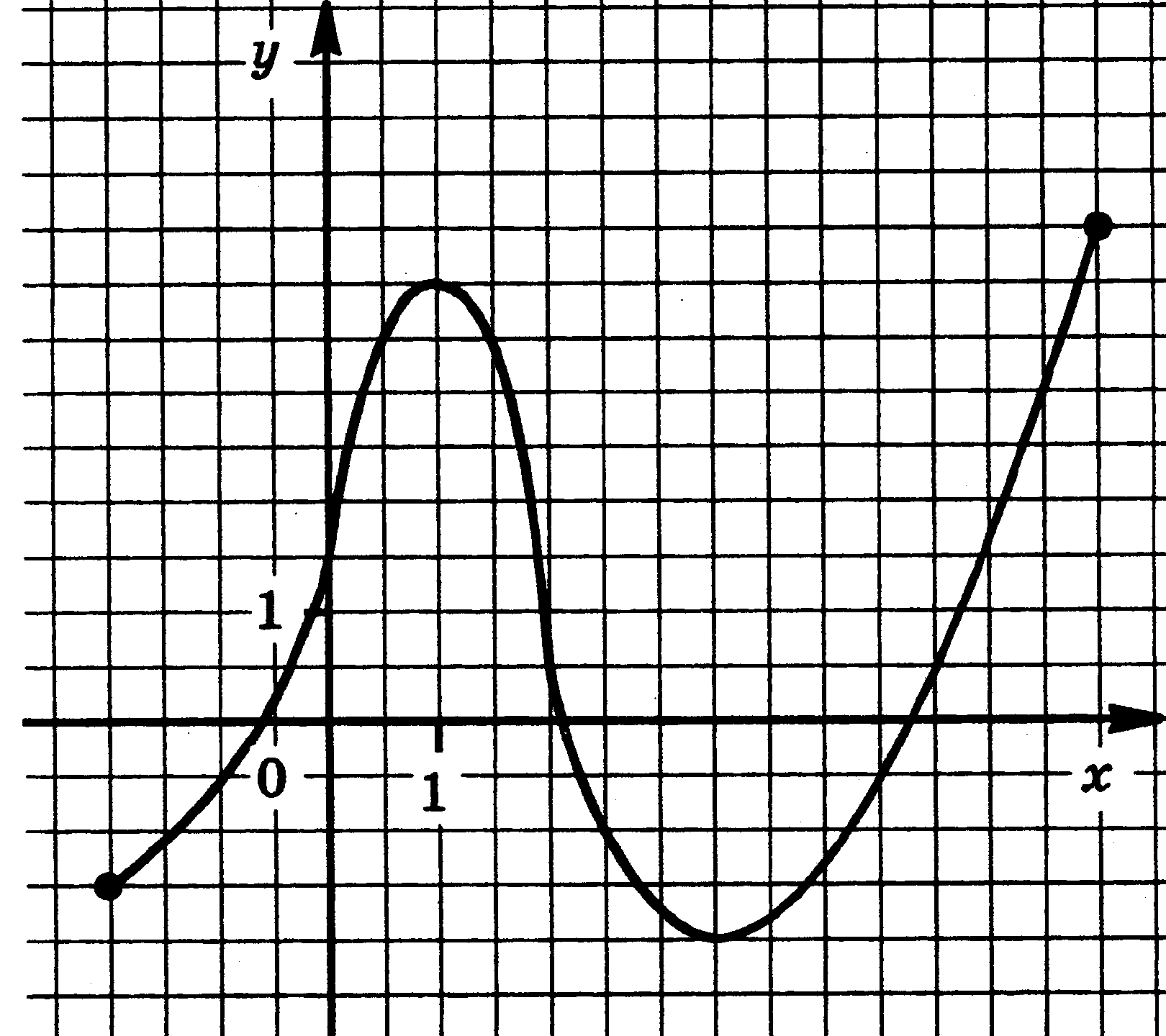 |
| 13. 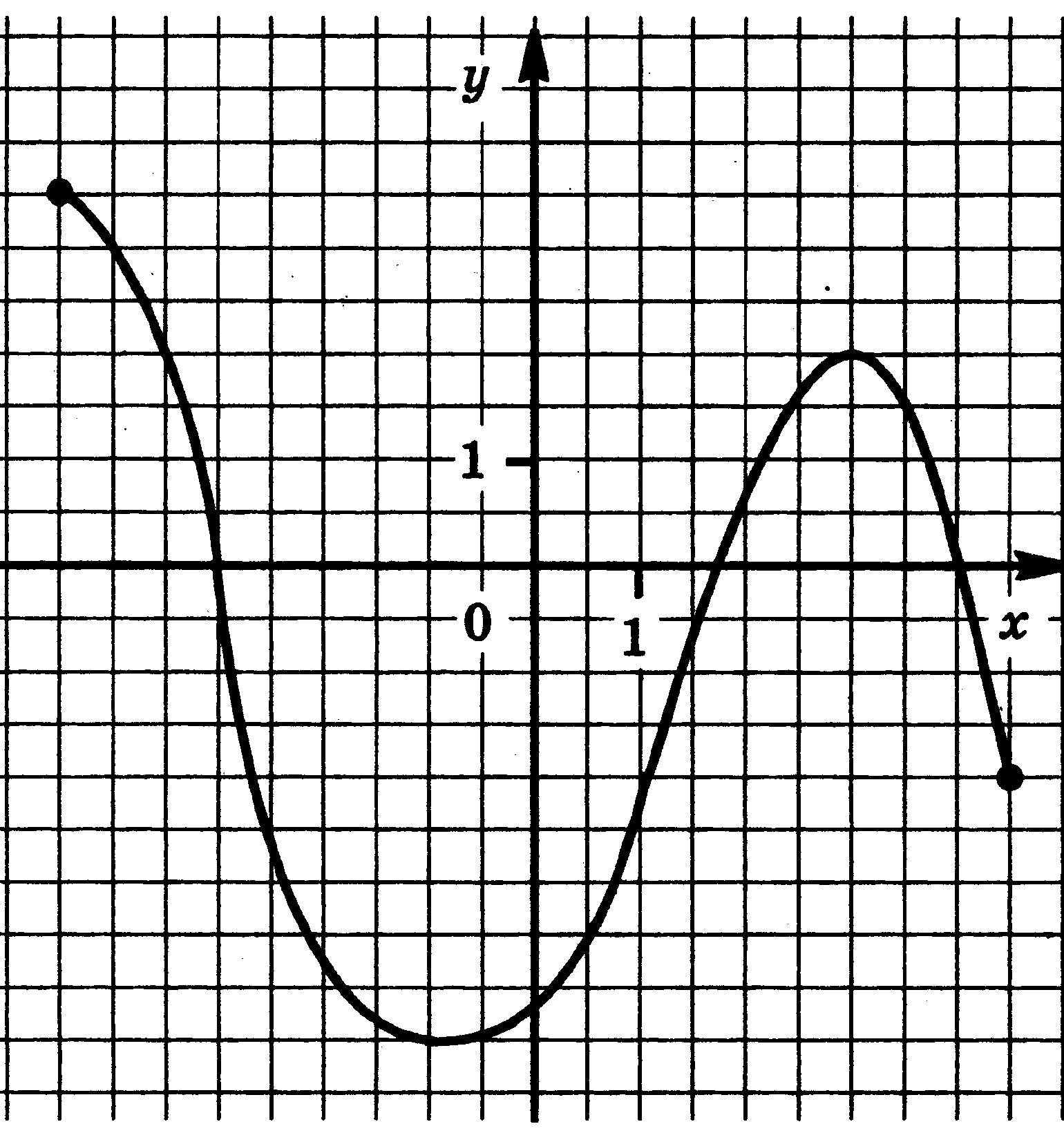 | 14. 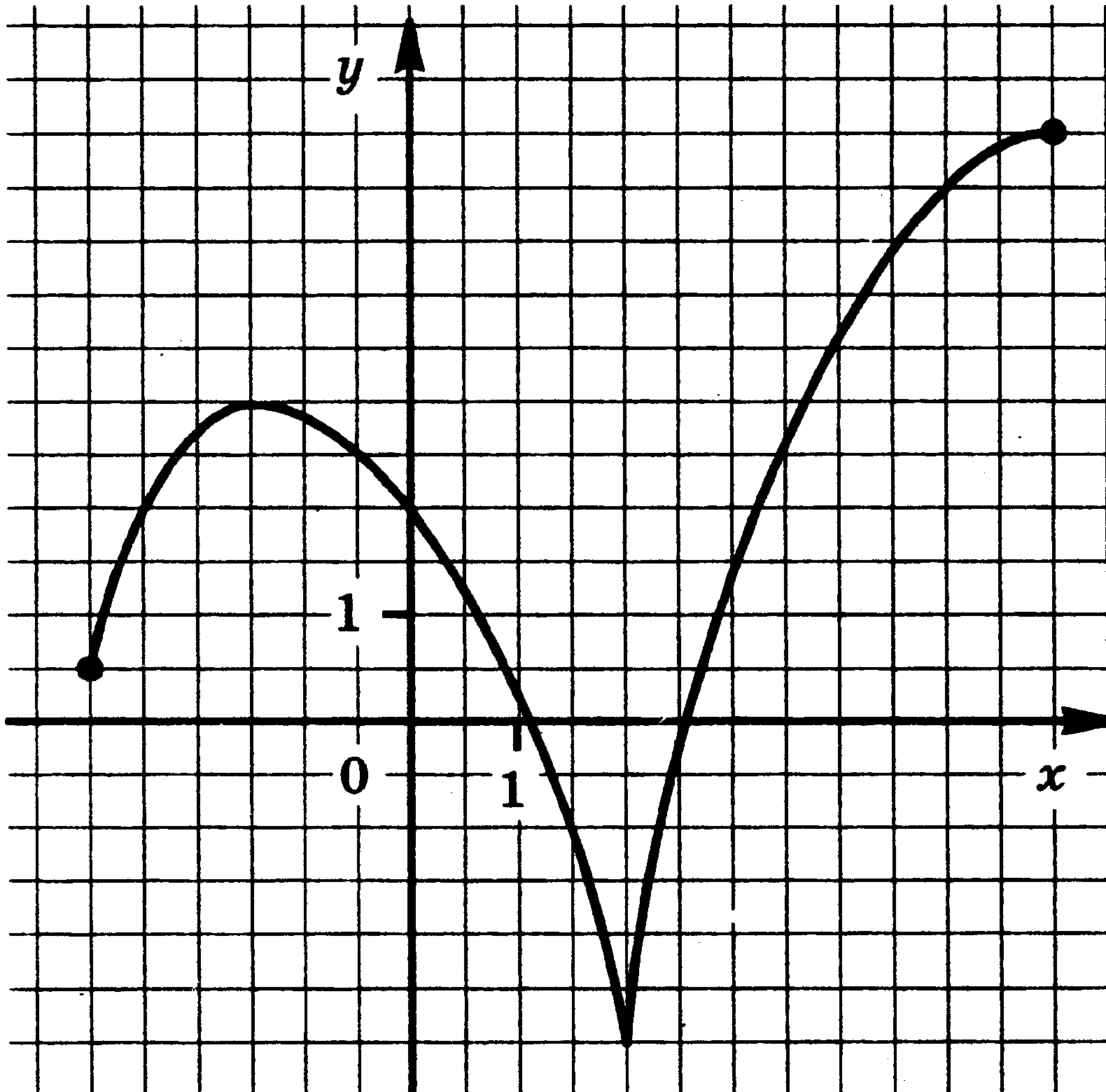 |
| 15. 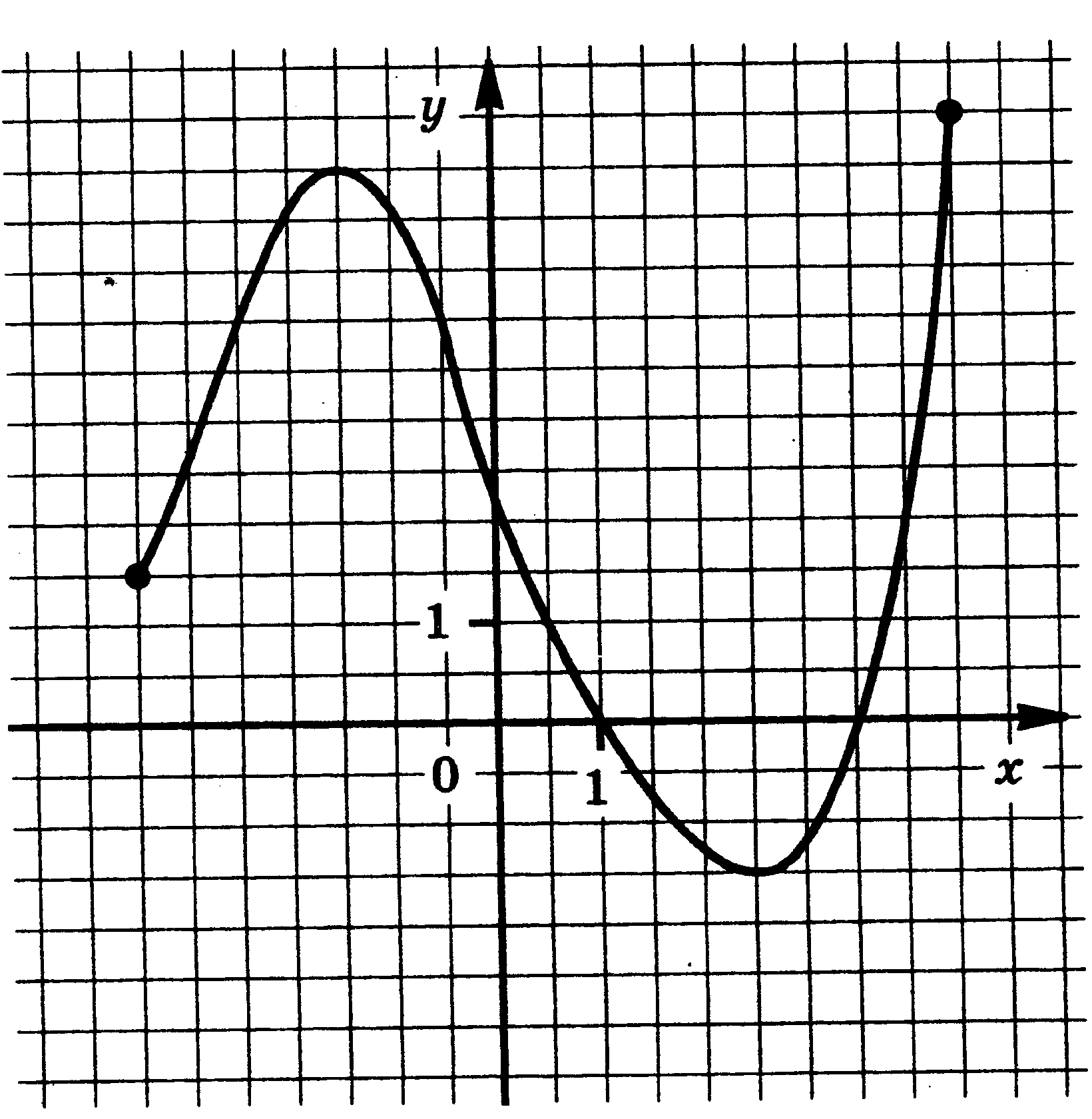 | 16. 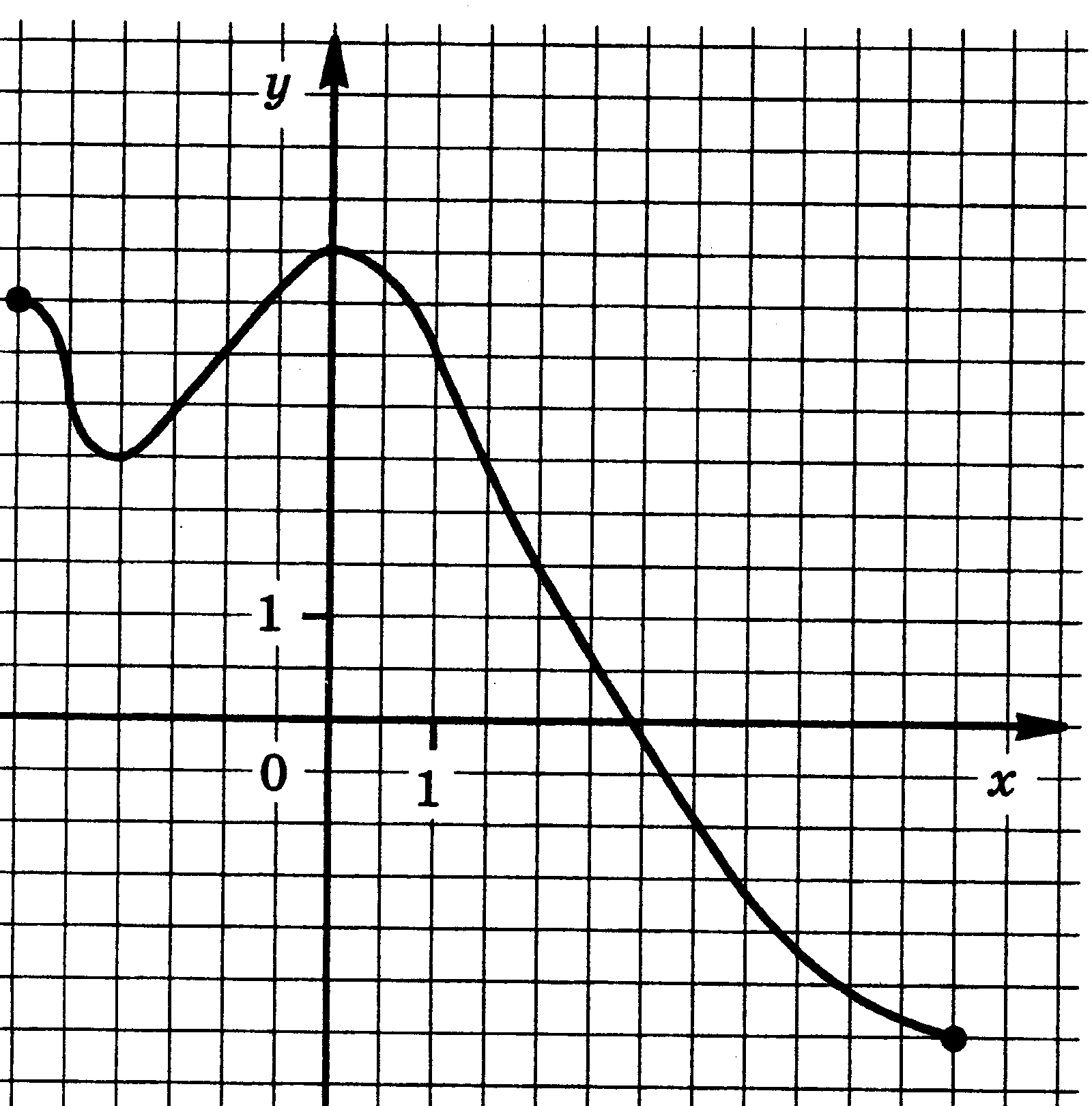 |
| 17. 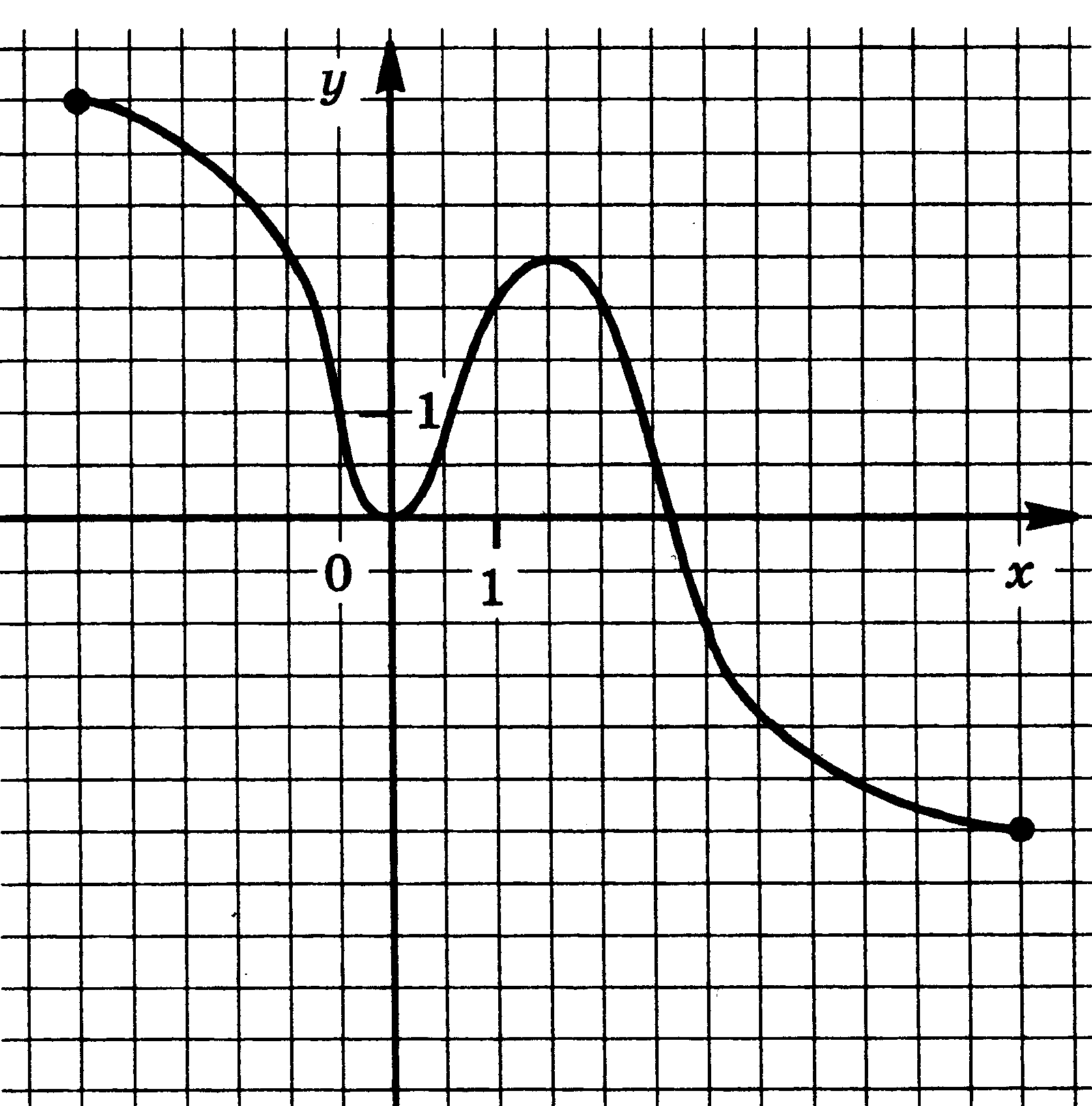 | 18. 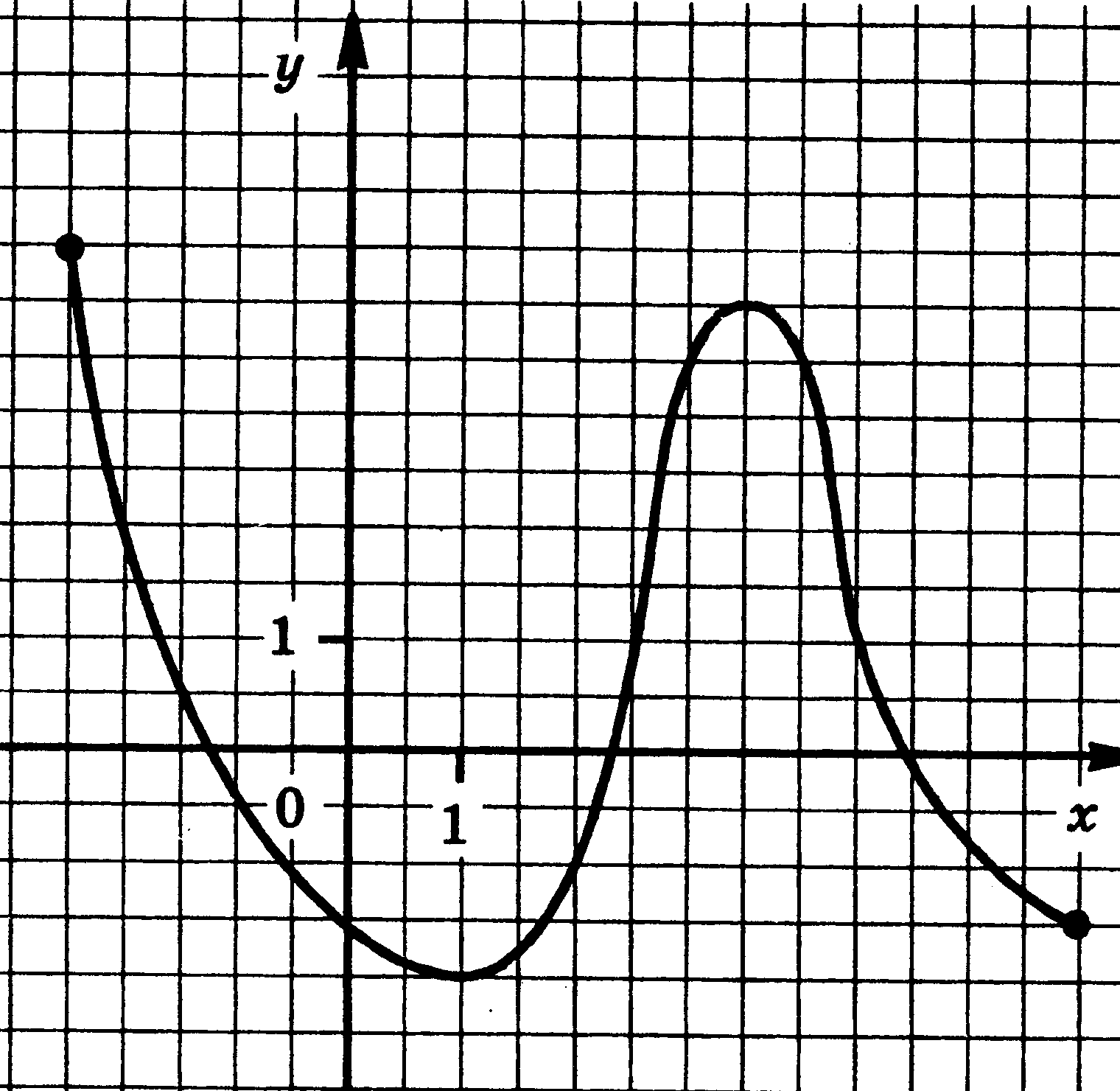 |
| 19. 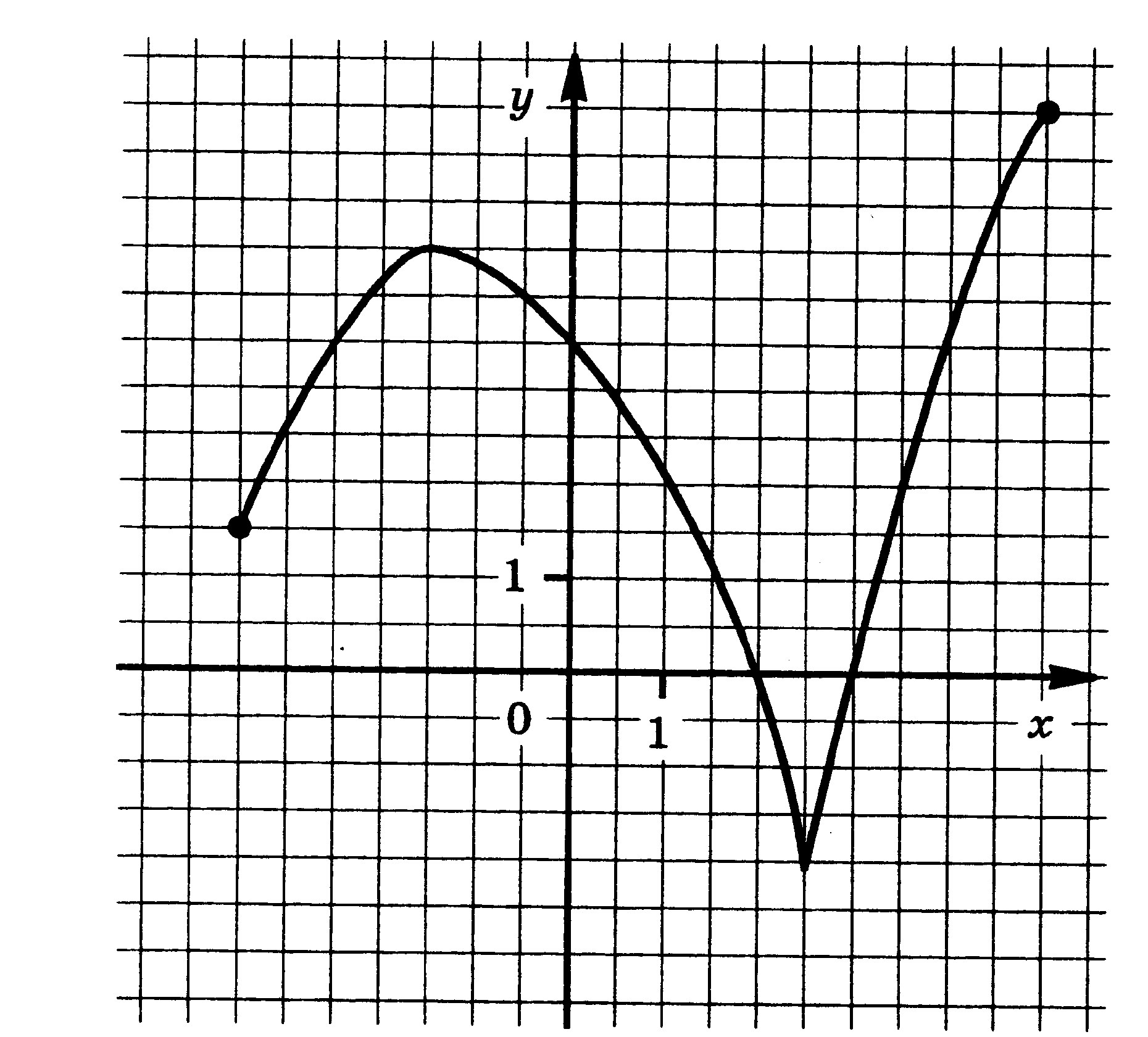 | 20. 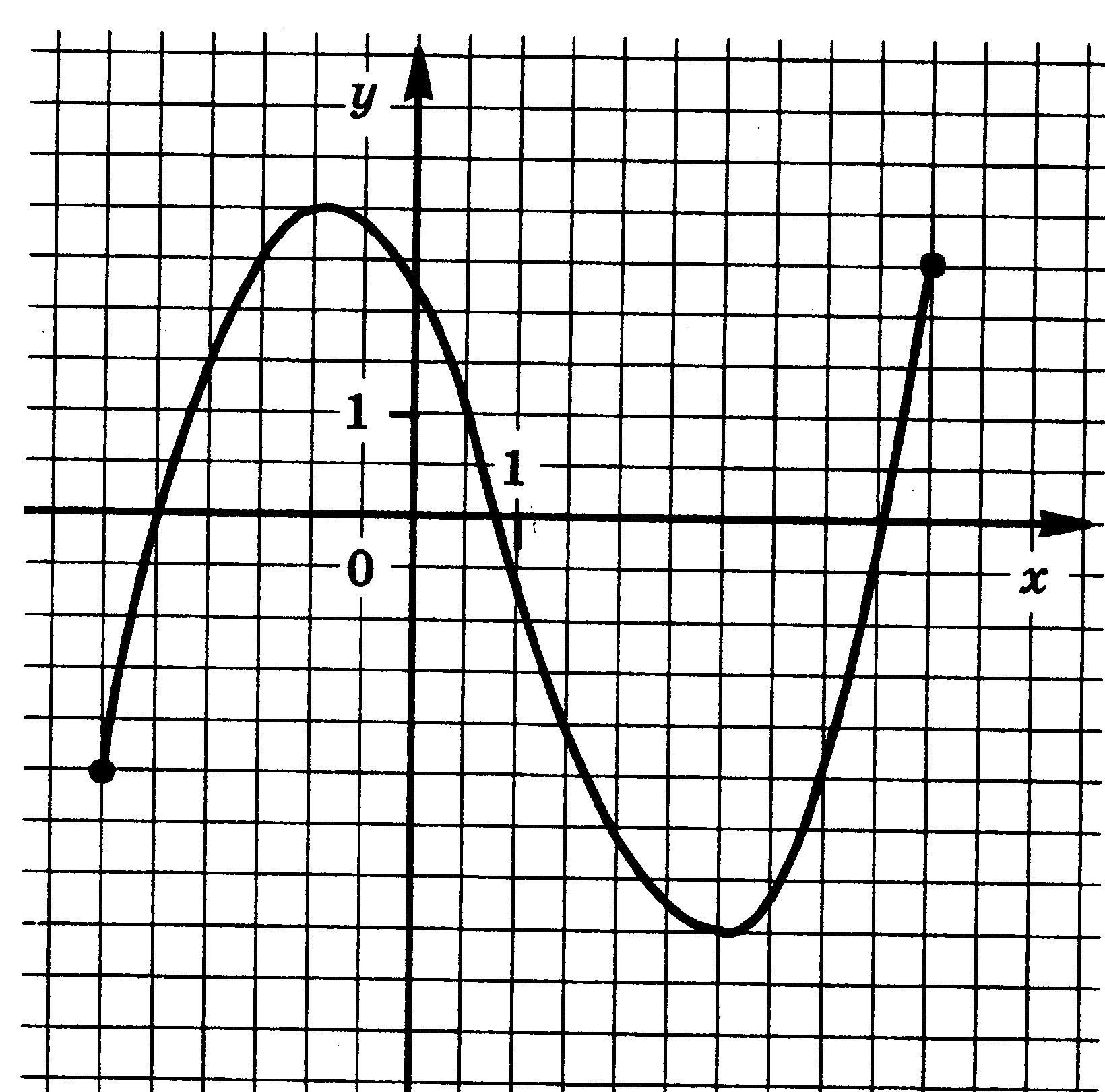 |
5. Производная и ее применения.
Найдите интервалы возрастания и убывания функции, определите вид точек экстремума:
|
|
6. Задачи планиметрии.
-
Периметр треугольника ABC равен 20. Найдите периметр треугольника FDE, вершинами которого являются середины сторон треугольника ABC.
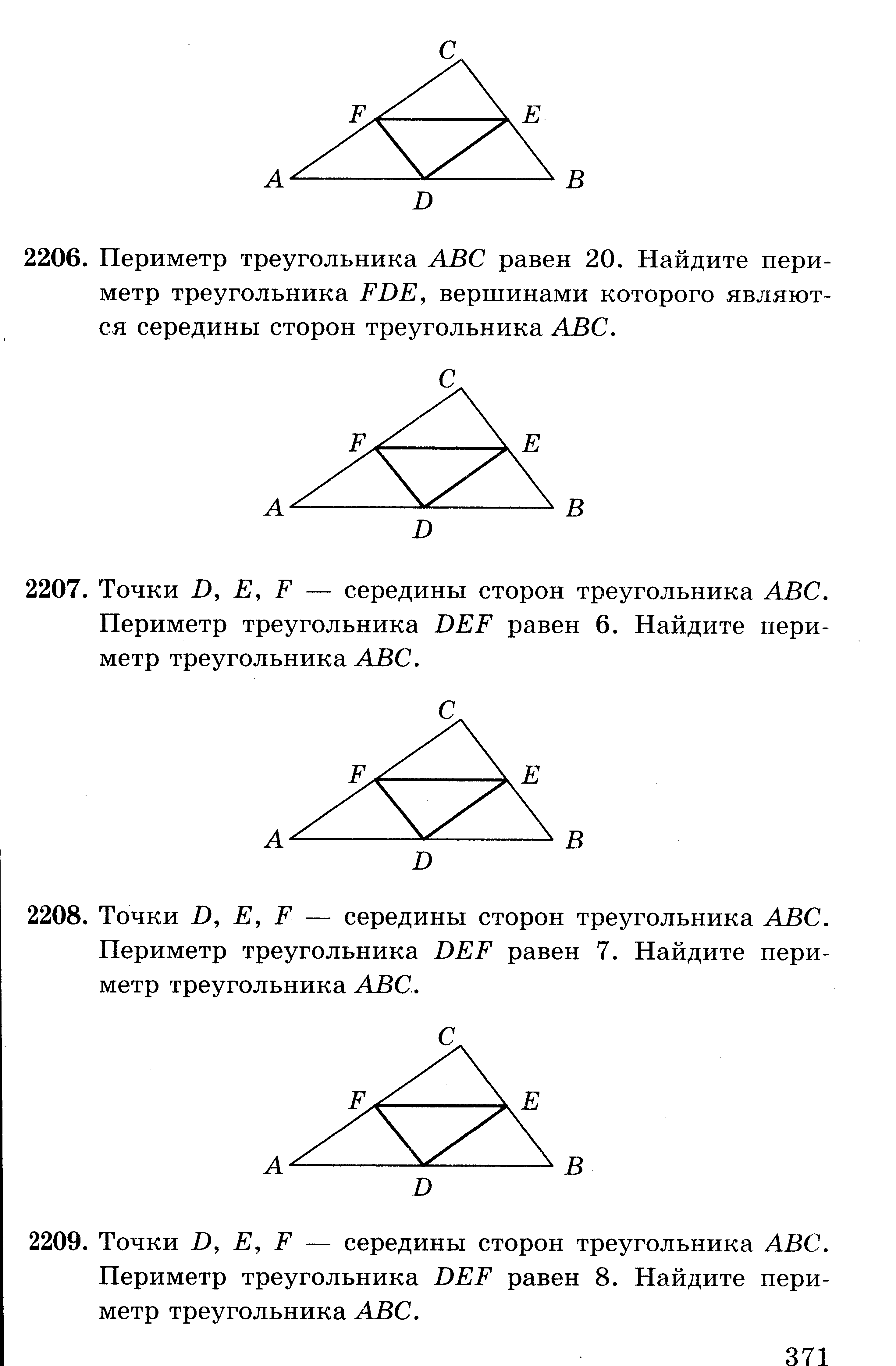
-
Точки D, Е, F — середины сторон треугольника ABC. Периметр треугольника DEF равен 6. Найдите периметр треугольника ABC.

-
Точки D, Е, F — середины сторон треугольника ABC. Периметр треугольника DEF равен 7. Найдите периметр треугольника ABC.

-
Точки D, Е, F — середины сторон треугольника ABC. Периметр треугольника DEF равен 8. Найдите периметр треугольника ABC.

-
Периметр треугольника ABC равен 16. Найдите периметр треугольника FDE, вершинами которого являются середины сторон треугольника ABC

-
Периметр треугольника ABC равен 18. Найдите периметр треугольника FDE, вершинами которого являются середины сторон треугольника ABC

-
Периметр параллелограмма равен 46 см. Меньшая сторона равна 9 см. Найдите большую сторону параллелограмма. -
Периметр параллелограмма равен 26 мм. Меньшая сторона равна 3 мм. Найдите большую сторону параллелограмма. -
Периметр параллелограмма равен 44 см. Меньшая сторона равна 10 см. Найдите большую сторону параллелограмма. -
Периметр параллелограмма равен 70 мм. Большая сторона равна 18мм. Найдите меньшую сторону параллелограмма. -
Периметр параллелограмма равен 54 см. Большая сторона равна 17см. Найдите меньшую сторону параллелограмма. -
Периметр параллелограмма равен 42 см. Большая сторона равна 19см. Найдите меньшую сторону параллелограмма.
-
Середины последовательных сторон прямоугольника, диагонали которого равны 7дм, соединены отрезками. Найдите периметр образовавшегося четырехугольника.
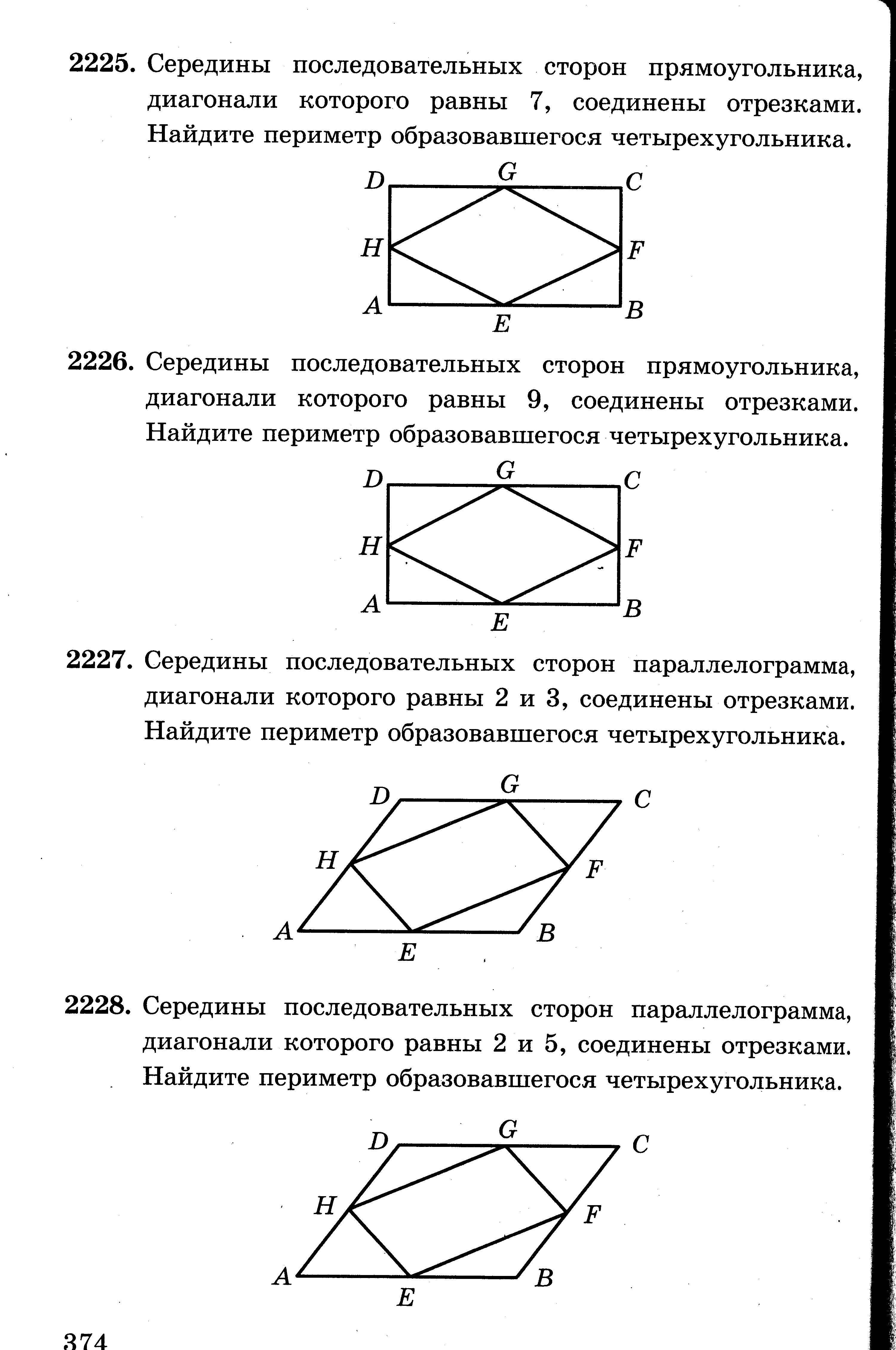
-
Середины последовательных сторон прямоугольника, диагонали которого равны 9см, соединены отрезками. Найдите периметр образовавшегося четырехугольника.

-
Середины последовательных сторон прямоугольника, диагонали которого равны 5см, соединены отрезками. Найдите периметр образовавшегося четырехугольника.

-
Середины последовательных сторон параллелограмма, диагонали которого равны 2см и 3см, соединены отрезками. Найдите периметр образовавшегося четырехугольника.

-
Середины последовательных сторон параллелограмма, диагонали которого равны 2дм и 5дм, соединены отрезками. Найдите периметр образовавшегося четырехугольника.

-
Середины последовательных сторон параллелограмма, диагонали которого равны 2дм и 9дм, соединены отрезками. Найдите периметр образовавшегося четырехугольника.

19) Средняя линия трапеции равна 13 см, а меньшее основание равно 11 см. Найдите большее основание.
20) Средняя линия трапеции равна 17 дм, а большее основание равно 27 дм. Найдите меньшее основание трапеции.
7. Многогранники и их свойства.
-
В кубе ABCDA'B'C'D' из вершины D' проведены диагонали граней D'A, D'B' и D'C. Сделайте рисунок. Как называется многогранник с вершинами A, B', C, D'? Имеет ли этот многогранник равные ребра? равные грани? -
В кубе ABCDA'B'C'D' отмечены следующие точки: К — центр грани ВСС'B',L — центр грани DCC'D' и М — центр грани ABCD. Сделайте рисунок. Как называется многогранник CKLM? Имеет ли этот многогранник равные ребра? равные грани? -
Точки пересечения высот всех граней правильной треугольной пирамиды являются вершинами некоторого многогранника. Как называется этот многогранник? Имеет ли он равные ребра? равные грани? -
Вершинами некоторого многогранника являются центр верхней грани куба и середины всех сторон нижней его грани. Как называется этот многогранник? Сделайте рисунок и обозначьте равные ребра многогранника; укажите, какие грани этого многогранника равны между собой. -
На какие многогранники разбивает призму АВСА'В'С' плоскость, проходящая через вершины А,В,С'? Сделайте рисунок. -
Сечение параллелепипеда ABCDA'B'C'D' проведено через точки А, В и середину ребра CC'.Каким многоугольником является это сечение? Сделайте рисунок и отметьте равные стороны многоугольника. -
Куб рассечен плоскостью, проходящей через середины двух смежных сторон нижнего основания и центр верхнего основания. Как называется многоугольник, полученный в сечении? Сделайте рисунок и отметьте равные стороны этого многоугольника. -
На какие многогранники разбивается параллелепипед ABCDA'B'C'D' плоскостью, проходящей через вершины A,B'и D? Какие особенности имеют эти многогранники? Сделайте рисунок. -
Вершинами многогранника являются середины сторон основания и середина высоты правильной четырехугольной пирамиды. Как называется этот многогранник? Сделайте рисунок и отметьте равные ребра этого многогранника. -
Точки пересечения диагоналей всех граней правильной четырехугольной призмы являются вершинами некоторого многогранника. Сделайте рисунок и отметьте равные ребра этого многогранника. -
Сечение правильной треугольной призмы АВСА'В'С' проходит через ребро АВ и точку пересечения медиан основания А'В'С'. Каким многоугольником является это сечение? Сделайте рисунок и отметьте равные стороны этого многоугольника. -
Вершинами многогранника являются середины боковых ребер и центр основания правильной пирамиды. Как называется этот многогранник? Сделайте рисунок и отметьте равные ребра этого многогранника. -
Вершины некоторого многогранника являются центрами пяти граней куба. Как называется этот многогранник? Сделайте рисунок и отметьте равные ребра этого многогранника. -
На какие многогранники разбивает прямую призму АВСА'В'С' плоскость, проходящая через вершины А, В и С' ? Сделайте рисунок. -
В кубе ABCDA'B'C'D' проведено сечение через середины ребер АВ и AD и вершину С'. Каким многоугольником является это сечение? Сделайте рисунок и отметьте равные стороны этого многоугольника. -
) В кубе ABCDA'B'C'D' из вершины D' проведены диагонали граней D'A, D'B' и D'C. Сделайте рисунок. Как называется многогранник с вершинами A, B', C, D'? Имеет ли этот многогранник равные ребра? равные грани? -
Вершинами некоторого многогранника являются центр верхней грани куба и середины всех сторон нижней его грани. Как называется этот многогранник? Сделайте рисунок и обозначьте равные ребра многогранника; укажите, какие грани этого многогранника равны между собой. -
В кубе ABCDA'B'C'D' отмечены следующие точки: К — центр грани ВСС'B',L — центр грани DCC'D' и М — центр грани ABCD. Сделайте рисунок. Как называется многогранник CKLM? Имеет ли этот многогранник равные ребра? равные грани? -
пересечения высот всех граней правильной треугольной пирамиды являются вершинами некоторого многогранника. Как называется этот многогранник? Имеет ли он равные ребра? равные грани? -
Вершинами многогранника являются середины сторон основания и середина высоты правильной четырехугольной пирамиды. Как называется этот многогранник? Сделайте рисунок и отметьте равные ребра этого многогранника.
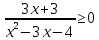
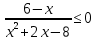
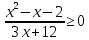
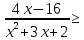 0
0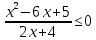
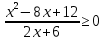
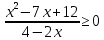
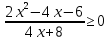
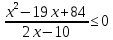
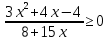
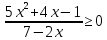
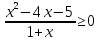
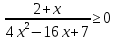
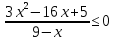
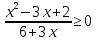
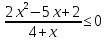
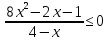
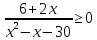
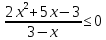
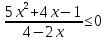
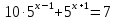
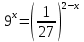
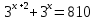 .
.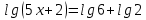
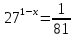
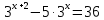
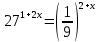
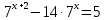
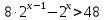
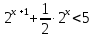
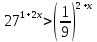
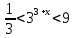
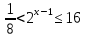
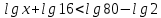
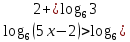
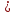 -3
-3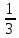 x3 + 5x2 – 1
x3 + 5x2 – 1 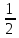 x4 – 8
x4 – 8