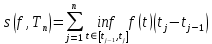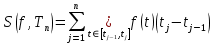и к одному и тому же пределу была основана на том, что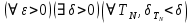





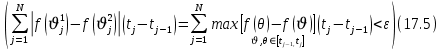
Рассмотрим произвольную ограниченную функцию 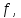заданную на . Введём следующее определение

Определение 17.6. Пусть 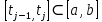. Величину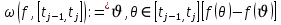



назовём колебанием функции на отрезке .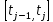

Использую введённое понятие и его обозначение перепишем формулу 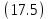в виде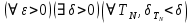





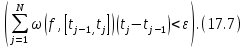
Обратим внимание на то, что для выполнения условия 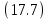непрерывность функции необязательна. В самом деле рассмотрим неубывающую на ограниченную функцию 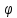. Ясно, что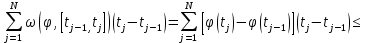





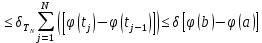
Выбирая



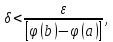
получаем, что для разбиений, мелкость которых меньше таким образом выполненного 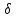условие 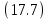выполняется. Так как неубывающая функция может иметь бесконечное (но не более чем счётное) число точек разрыва, то мы видим, что условие 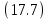выполняется и для разрывных функций с , вообще говоря бесконечным числом точек разрыва.

---

Докажем теперь следующую теорему.

Теорема 17.8. Для того, чтобы ограниченная на отрезке функция была интегрируема по Риману достаточно, чтобы выполнялось следующее условие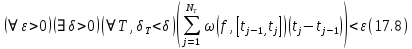



Здесь 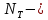число отрезков разбиения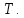

Доказательство. Пусть условие (17.8) выполнено. Будем считать поначалу монотонная последовательность разбиений, 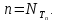Обозначим через 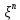набор 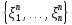промежуточных точек 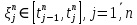отрезков 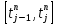разбиения . Обозначим через



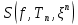
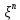сумму Римана функции для заданного разбиения и выбранного набора промежуточных точек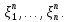

Докажем, что для монотонной последовательности последовательность 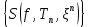является фундаментальной. Действительно, пусть 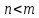. Оценим ,



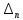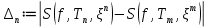
Рассмотрим отрезок 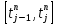разбиения . Пусть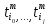

---

все точки разбиения 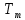, принадлежащие 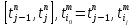= 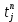, так что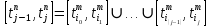



Ясно, что 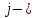й член суммы

имеет вид

=



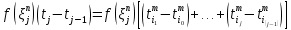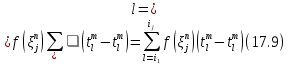
Соответствующая этому члену суммы

Группа слагаемых определяемая отрезками 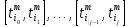, составляющими отрезок имеет вид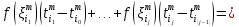



Таких групп слагаемых в сумме



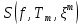
столько же , сколько отрезков , а именно , слагаемых. Поэтому



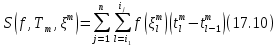
При этом в соответствии с (17.9) получим



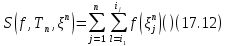
Используя теперь 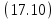и 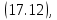получим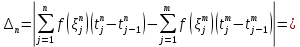







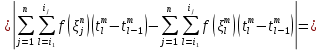
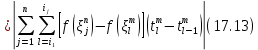
Точки



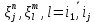
Принадлежат одному т тому же отрезку для любого 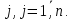Поэтому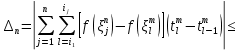

---

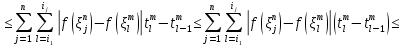
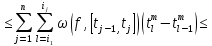
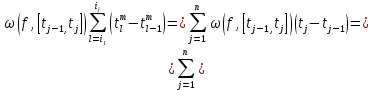
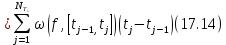
Выберем теперь столь большим, чтобы мелкость разбиения была меньше из (17.8). Тогда из (17.8) и (17.14) получим,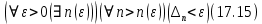



Предложение (17.15) означает, что для монотонной последовательности разбиений последовательность частичных сумм, мелкость разбиения которых стремится к нулю, является сходящейся.

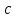
Пользуясь приёмом сравнения несравнимых 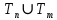, получаем, что



сходится для любой последовательности разбиений, чья мелкость стремится к нулю.

Теорема доказана.

Лекция 18.

Теорема 17.8 даёт нам очень полезный критерий интегрируемости функций по Риману. Замечу теперь, что при рассмотрении вопроса об интегрируемости функций мы постоянно требуем их ограниченности. Покажем, что это условие действительно является необходимым условием.

Теорема 18.1. Пусть функция 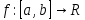интегрируема на 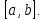В таком случае эта функция является ограниченной, т.е.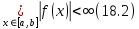



Доказательство. Допустим, что условие (18.2) не выполняется. Тогда существует последовательность 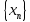, такая что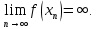

Отрезок является компактным множеством. Поэтому существует подпоследовательность 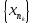и точка 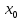, такие что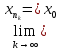



Рассмотрим теперь произвольное разбиение

---

отрезка . Пусть 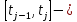которому принадлежит . Пусть 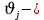промежуточная точка этого отрезка, входящая в 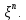Какой бы ни была длина и каким бы ни было значение суммы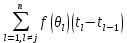



Мы можем подобрать 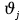столь близким к , что значение суммы Римана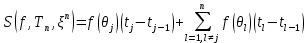



Будет больше наперёд заданного 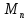. Выбирая бесконечно большую последовательность 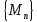, мы получим , что предел интегральных сумм Римана равен бесконечности при таких выборах промежуточных точек. Но он должен быть конечным при любом их выборе. Полученное противоречие означает, что интегрируемая по Риману функция должна быть ограниченной.

Теорема доказана.

Доказанная теорема, в частности, показала, что от выбора промежуточных точек при вычислении сумм Римана многое зависит. Поэтому для доказательства существования интеграла Римана, равного конечному пределу интегральных сумм нам действительно всякий раз проверять, что он не зависит от выбора множеств промежуточных точек.

Дарбу был предложен иной подход к понятию интеграла, в котором зависимость от выбора промежуточных точек отсутствует.

Определение 18.3. Пусть заданное отображение. Для произвольного разбиения нижнюю 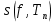и верхнюю 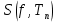суммы Дарбу следующим образом

---

Смотрите также файлы

• Определите обозначенные периоды, относящиеся ко времени отдыха.doc

• Локальные компьютерные сети Компьютерная сеть.docx

• В принадлежности лица к категории вероятных объектов преступного посягательства в в чем проявляется ролевая виктимность в принадлежности.docx

• There is an even greater in light of all the things.docx

• Внешнее строение корневища, клубня и луковицы.docx