Заметим, что в случае непрерывной функции нижняя интегральная сумма Дарбу совпадает с суммой Римана, а верхняя интегральная сумма Дарбу совпадает с суммой Римана.

В случае непрерывной функции сходимость интегральных сумм обеспечила сходимость интегральных сумм Римана для произвольного выбора промежуточных точек. Поэтому такого рода обобщение понятия интегральной суммы представляется естественным. Естественным же является следующее определение интеграла Дарбу.

Определение 18.4. Пусть заданное отображение. Мы будем говорить, что функция интегрируема по Дарбу, если конечные пределы последовательностей 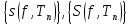интегральных сумм Дарбу существуют и совпадают между собой.

Замечание18.5. В обозначении интегральной суммы Римана в общем случае указана зависимость от системы промежуточных точек разбиения. В обозначениях интегральных сумм Дарбу она естественным образом отсутствует.

Мы не вводим специального обозначения для интеграла Дарбу, так как, как показывает следующая теорема, интегралы Римана и Дарбу совпадают между собой.

Теорема 18.6. Функция интегрируема по Риману тогда и только тогда, когда она интегрируема по Дарбу.

Доказательство. Определение интеграла Дарбу показывает, что в обоих случаях мы должны рассматривать лишь ограниченные функции.

Заметим далее, что для произвольного разбиения

---

и при произвольном выборе множества промежуточных точек имеет место очевидное неравенство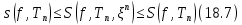



Из неравенств (18.7) следует, что если интеграл Дарбу существует, то интеграл Римана также существует.

Допустим теперь, что интеграл Римана существует. Последовательность нижних интегральных сумм Дарбу в этом случае ограничена сверху, а верхних снизу. Последовательность нижних интегральных сумм Дарбу представляет собой неубывающую последовательность, верхних невозрастающую. Это означает, что пределы последовательностей существуют. Осталось показать, что они совпадают между собой.

Для произвольного разбиения мы можем выбрать две системы 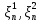промежуточных точек так, что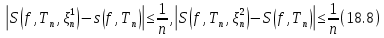



Так как пределы интегральных сумм Римана существуют независимо от выбора систем промежуточных точек и совпадают между собой, то из (18.8) следует, что пределы сумм Дарбу, существование которых было доказано, совпадают между собой. Это означает существование интеграла Дарбу.

Теорема доказана.

Доказанная теорема позволяет уточнить теорему 17.8

Теорема18.9 Для того, чтобы ограниченная на отрезке функция была интегрируема по Риману необходимо и достаточно, чтобы выполнялось следующее условие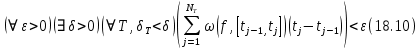

.

Здесь число отрезков разбиения

Упражнение 18.11. Доказать теорему 18.9.

Замечание 18.12. Введение интеграла Дарбу помимо возможности избавиться от необходимости рассмотрение различных выборов промежуточных точек предоставляет и иные возможности.

---

Иногда для получения необходимых при рассмотрении той или иной задачи для получения нужных оценок достаточно существования одного из пределов



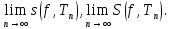
Первый из этих пределов называется нижним интегралом Дарбу, второй верхним интегралом Дарбу.

Доказанные нами теоремы и полученные с их помощью примеры интегрирумых функций указывают на то, что существенную роль в вопросе об интегрируемости играет массивность множества точек разрыва функций.

Так функция Дирихле, принимающая значение нуль в иррациональных точках отрезка 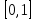и значение, равное единице 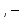в рациональных , очевидно, не интегрируема по Риману. В то же время любая монотонная функция, заданная на этом отрезке, является интегрируемой. При этом такая функция может иметь бесконечное число точек разрыва.
Естественно задаться вопросом о том, что представляет собой необходимое и достаточное условие, налагаемое на множество точек разрыва и обеспечивающее интегрируемость функции с таким точек разрыва по Риману. Это условие было получено Лебегом. Для того, чтобы сформулировать это условие введём следующее определение.

Определение18.13. Пусть 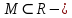множество. Будем говорить, что его внешняя мера Лебега равна нулю, если его можно покрыть объединением интервалов, сумма длин которых может быть произвольно малым , т.е.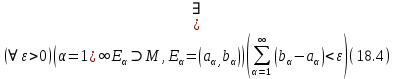



Упражнение 18.14. Показать, что множество Кантора имеет внешнюю меру Лебега, равную нулю.

Теорема 18.15 (Лебег). Для того, чтобы ограниченная функция была интегрируема по Риману необходимо и достаточно, чтобы множество её точек разрыва имело нулевую внешнюю меру Лебега.

С помощью этой теоремы, доказательство будет дано позже, покажем, что существуют интегрируемые по Риману функции с несчётным множеством точек разрыва.

Пусть функция

---

, функция определённая следующим образом. Рассмотрим процедуру построения множества Кантора. Полагаем равной единице на интервале 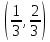. Затем полагаем её равной единице на правом из выбрасываемых на следующем шаге интервале и минус единице- на левом и так далее. В результате получим функцию, определённую всюду за исключением несчётно множества Кантора, имеющего нулевую внешнюю меру Лебега. В точках множества Кантора положим её равной нулю. Ясно, в каждой множестве Кантора функция разрывна, ибо пределы в ней не существуют. Вместе с тем она в соответствие с теоремой Лебега является интегрируемой по Риману.

---

Смотрите также файлы

• Определите обозначенные периоды, относящиеся ко времени отдыха.doc

• Локальные компьютерные сети Компьютерная сеть.docx

• В принадлежности лица к категории вероятных объектов преступного посягательства в в чем проявляется ролевая виктимность в принадлежности.docx

• There is an even greater in light of all the things.docx

• Внешнее строение корневища, клубня и луковицы.docx