Файл: Протокол 1 от 28 августа 2020 г. Конспект лекций содержание введение Краткая характеристика дисциплины.doc

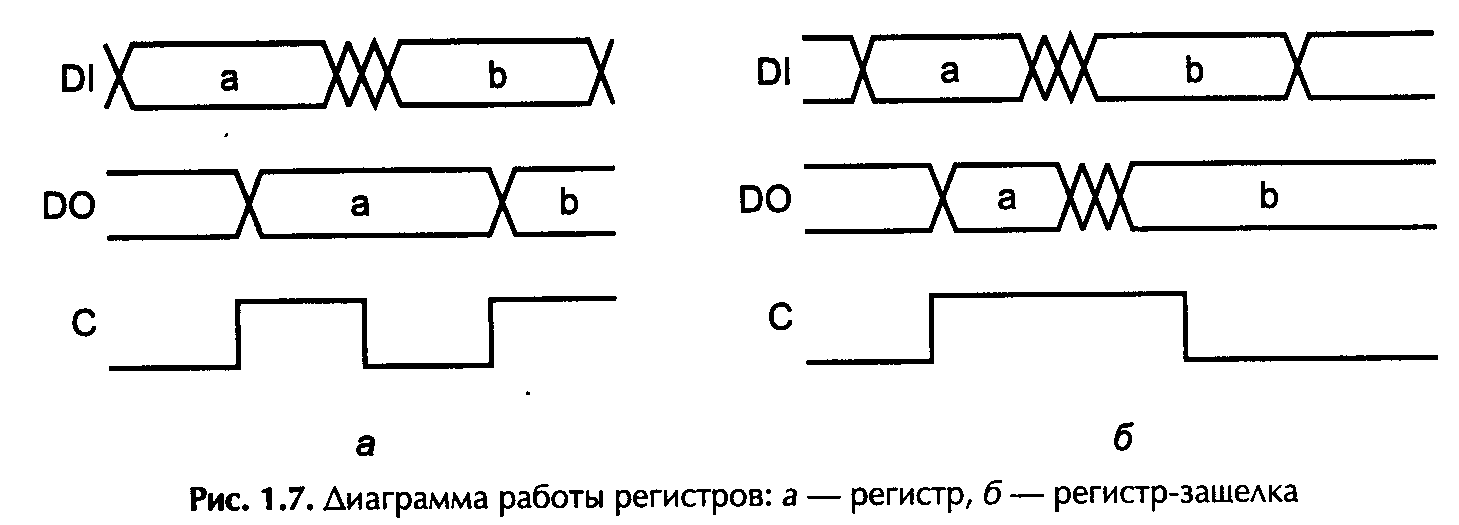
Логические схемы могут быть чисто комбинационными вентилями (Gate), у которых состояние выходов определяется только текущим состоянием входов, а могут быть и элементами с памятью. В схемах последнего типа состояние выхода определяется и предысторией входных сигналов и внутренних состоя­ний. К этим схемам относятся разнообразные триггеры, регистры, счетчики и т. п. Элементы могут быть асинхронными и синхронными. У последних со­стояние входов (всех или части) стробируется потенциалом или перепадом на специальном входе синхронизации. Здесь следует особо отметить два типа эле­ментов, широко применяемых в микропроцессорной технике: Регистром (Regis­ter) называют совокупность нескольких запоминающих элементов, запись в которые производится по общему управляющему сигналу. Обычно подразуме­вается, что в регистре информация фиксируется по перепаду сигнала синхро­низации (рис. 1.7, а, где запись происходит по положительному перепаду). Защелкой (Latch), или регистром-защелкой, называют схему, работающую иначе (рис. 1.7, б). Здесь при одном состоянии управляющего входа (на данном ри­сунке высоком) регистр «прозрачен» — на выходе отражаются изменения на входах, а при переходе этого сигнала в другое состояние на выходах фиксиру­ется состояние, присутствующее к этому моменту. Защелки используются для фиксации адреса на шине микропроцессора, позволяя схемам дешифраторов адреса раньше начинать работу, тем самым сокращая затраты времени на де­шифрацию адреса. Однако следует помнить, что до срабатывания на выходе защелки возможен «мусор» от переходных процессов на входе, чего не бывает в регистрах, синхронизируемых по перепаду. Для того чтобы любая синхрони­зируемая схема зафиксировала желаемое состояние, сигналы на входах должны установиться до синхронизирующего перепада за некоторое время, называемое временем установки tsetup, и удерживаться после него в течение времени удер­жания thold. Значение этих параметров определяется типом и быстродействием синхронизируемой схемы, и в пределе один из них (но не оба сразу!) может быть нулевым.

1.3.6 Сравнительная характеристика ЛЭ
Самыми распространенными на сегодняшний день являются ИС, реализующие ТТЛ и ее разновидности. Этот тип интегральных схем, судя по прогнозам специалистов, останется наиболее массовым и в ближайшем будущем.

---

Интегральные схемы данного типа обладают средним быстродействием (f 20– 50 МГц) и средней потребляемой мощностью.

ИС, реализующие ЭСЛ, являются наиболее быстродействующими, но мощность, потребляемая этими элементами, превышает мощность элементов ТТЛ. Однако гибкость схемотехнических решений ЭСЛ позволяет достаточно просто реализовать сложные логические функции.

В таблице 1 приведено сравнение элементов различных логик по основным параметрам, причем значение 1 соответствует лучшему значению параметра, а 7 — худшему.
Таблица 20 - Сравнительные характеристики логических элементов различных типов логик

Тип элемента	Быстро действие	Рассеиваемая мощность	Разветвление по входу	Помехоустойчивость
ТТЛ	3	4	4	4
ТТЛШ	2	5	4	4
p-МОП	7	2	2	2
n-МОП	5	2	2	3
КМОП	6	1	1	1
ЭСЛ	1	6	3	4
И2Л	4	3	4	4

Выводы

1. В настоящее время в БИС преимущественно используются логические схемы на МДП-транзисторах.

2. Из схем на биполярных транзисторах применяют схемы ТТЛ, ТТЛШ, ЭСЛ и И²Л.

3. Схемы ЭСЛ обладают наибольшим быстродействием.

4. Схемы И²Л наиболее экономичны и позволяют создавать БИС с большой степенью интеграции.

5. Схемы ТТЛ наиболее универсальны — они хорошо согласуются с другими схемами, но по быстродействию и экономичности уступают схемам ЭСЛ и И²Л.

1.4 Анализ и синтез КЦУ
1.4.1 ЗАДАЧИ АНАЛИЗА И СИНТЕЗА КЦУ
Устройства, в которых передача информации осуществляется с помощью двоичных символов (цифры 0 и 1) называются цифровыми.

Цифровые устройства подразделяются на два вида - КЦУ и ПЦУ.

КЦУ – комбинационное цифровое устройство – это логическое устройство, у которого значение функции на выходе зависит только от значения комбинации аргументов, присутствующей на его входе в данный момент времени и не зависит от предыдущего состояния устройства. Такое устройство не обладает памятью.

---

ПЦУ – последовательностное цифровое устройство – это логическое устройство, у которого значение функции на выходе зависит не только от значения комбинации аргументов, присутствующей на его входе в данный момент времени, но и от предыдущего состояния устройства. Это автомат с памятью.

Все цифровые устройства строятся на логических схемах, которые выполняют определенные логические функции.

Логическая функция состоит в обработке и преобразовании по определенным правилам входной информации в выходную. Сигнал на выходе (У) является функцией входного сигнала (аргумента) у = f(х₃ , х₂ , х₁ ).

Логическая схема в общем случае представляет собой совокупность некоторых типов логических элементов и элементов памяти, объединенных между собой определенным образом и выполняющих простые логические операции (логические действия над аргументами). Чтобы построить (синтезировать) логическую схему, необходимо, в первую очередь, определить (проанализировать) основные функции цифрового устройства ЦУ, описать принцип его работы, а затем на основе этих данных выбрать из общего набора логических элементов те, которые в большей степени будут соответствовать заданным требованиям.

В логических схемах работа элементов, узлов и устройств описывается алгебраическими формулами. Логические схемы, выполняющие одни и те же функции, могут отличаться по числу входящих в них логических элементов и по способу их соединения. Более экономичные логические схемы проектируются с помощью специальных математических преобразований с использованием основных законов, теорем и тождеств алгебры логики. Логические формулы преобразуются к виду, который соответствует наиболее простой логической схеме, содержащей минимальное количество элементов. Поэтому указанное преобразование формул называется минимизацией. Построение логической схемы целесообразно вести по минимизированной форме.

Анализ – это логическое разложение (расчленение) целого на части, выделение отдельных его свойств или сторон. Анализ является процедурой, противоположной синтезу.

Синтез – это логическое соединение (сочетание) частей, признаков, свойств, сторон в единое целое.

Основными этапами синтеза являются:

1 Представление логической функции любым способом (составление таблицы истинности в зависимости от назначения устройства или предъявляемых к нему требований, Запись логического выражения в виде СНДФ или СНКФ);

---

2 Получение ее минимальной формы;

3 Построение логической схемы в заданном базисе и выбор элементной базы;

4 Проверка функционирования схемы.

1.4.2 Представление Логических Функций В ДСНФ и КСНФ
Алгебраический способ представления логической функции позволяет записать функцию в виде логического выражения (формулы). Например, или
Существует две основные формы записи логических функций:

- совершенная нормальная дизъюнктивная форма (СНДФ)

- совершенная нормальная конъюнктивная форма (СНКФ)
Логическая функция в форме СНДФ записывается по таблице истинности по значениям функции равным «1» (у=1).

Каждая комбинация входных сигналов (аргументов Х) на этих значениях функции записывается в виде логического произведения (конъюнкции). Причем, если входной сигнал в этой комбинации равен «0» (Х=0), то записывается его отрицание , если же он равен «1»(Х=1), то записывается его прямое значение Х.

Конечное выражение логической функции состоит из полученных комбинаций входных сигналов (конъюнкций), записанных через логическое сложение (дизъюнкцию).
Таблица 21- Таблица истинности КЦУ

№ набора	Знач.аргум. Х			Функция У
	Х3	Х2	Х1
0	0	0	0	0
1	0	0	1	0
2	0	1	0	0
3	0	1	1	1
4	1	0	0	0
5	1	0	1	1
6	1	1	0	1
7	1	1	1	1

---

В таблице 21 функция равна «1» (y=1) на следующих наборах аргументов: №3, №5, №6, №7. Запишем логические произведения для каждого указанного набора:
Набор №3:

Набор №5:

Набор №6:

Набор №7:



Для записи логической функции в форме СНКФ необходимо выбрать те комбинации (наборы) логических аргументов, где функция равна «0» (у=0).

Каждый набор аргументов необходимо представить в виде логического сложения (дизъюнкции). Причем, если входной сигнал равен «1» (Х=1), то записывается его отрицание (инверсия) . Если же он равен «0», то записывается его значение Х.

Конечное логическое выражение записывается в виде логических произведений (конъюнкций) наборов.

В таблице 1 функция у равна « 0» на следующих наборах аргументов: №0, №1, №2, №4. Запишем логические сложения для каждого указанного набора:

Набор №0:

Набор №1:

Набор №2:

Набор №4:


Запись функции в СНДФ или СНКФ зависит от того, как задана функция у:

если задано больше значений у=1, то функцию целесообразно записать в СНКФ, если больше значений у=0, то -в СНДФ.

Логическая функция может быть задана в форме НДФ или НКФ и не являться совершенной.

Функция несовершенна, если в записи логического выражения (в простом сложении для КФ или простом умножении для ДФ) отсутствует один и более аргументов Х, образующих функцию.

Если в ДФ в элементарном произведении или в КФ в элементарной сумме один и тот же аргумент Х или его инверсия

---