Файл: Протокол 1 от 28 августа 2020 г. Конспект лекций содержание введение Краткая характеристика дисциплины.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 402
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
не повторяется, то функция является нормальной.
Пример 3:
а) НДФ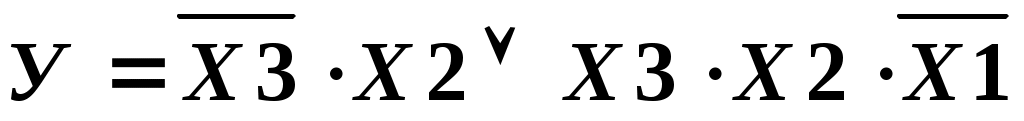
б) НКФ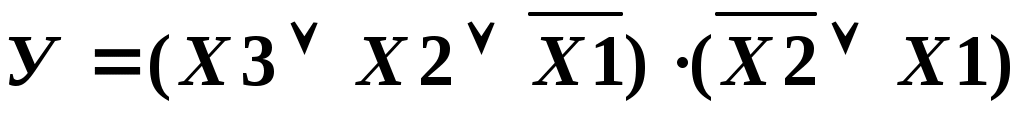
В примере 3 а) в первой простой конъюнкции отсутствует прямое значение аргумента Х1 или его инверсии;
В примере 3 б) во второй простой конъюнкции отсутствует значение аргумента Х3 или его инверсия.
В следующих двух выражениях функция не является нормальной и совершенной. Функция ДФ несовершенна, так как в первой простой конъюнкции отсутствует значение аргумента Х3 или его инверсия. Нормальный вид функции ДФ нарушает второе значение аргумента Х1 в первой простой конъюнкции и значение во второй.
во второй.
Совершенный вид функции КФ нарушает отсутствие значений Х1, Х3 и их инверсии в первой простой дизъюнкции, а также отсутствие значений Х1, Х2 и их инверсии на месте третьей простой дизъюнкции. Функция не является нормальной, так как на месте первой простой дизъюнкции приведены два одинаковых значения аргументов Х2.
ДФ
К
Ф
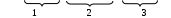
Цифровой способ записи позволяет получить компактное логическое выражение, в котором присутствуют номера наборов аргументов.
Для функции СНДФ под знаком суммы перечисляются номера наборов (в порядке возрастания), на которых функция принимает значение «1».
Все оставшиеся наборы функции (таблица 1) будут записываться под знаком произведения. На основании такой записи можно легко перейти к алгебраической записи логической функции.
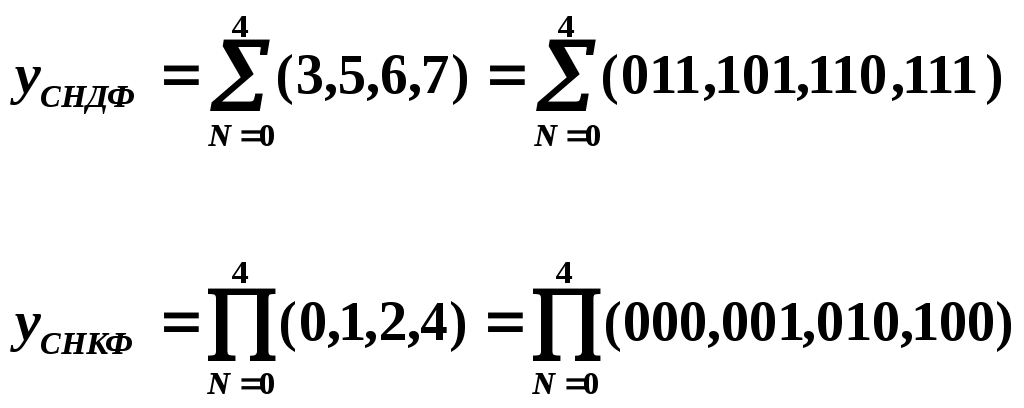
1.4.3 МИНИМИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
Общие сведения
Для того, чтобы построить логическую схему любого цифрового устройства, достаточно записать его логическую функцию в виде СНДФ или СНКФ, а затем реализовать ее с помощью простейших логических элементов.
Пример1: Логическая функция задана в форме СНДФ
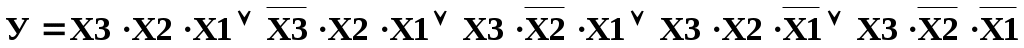
АНАЛИЗ. Для реализации схемы согласно выражения необходимо использовать 9 элементов:
3 элемента НЕ,
5 элементов 3И,
1 элемент 5ИЛ.
СИНТЕЗ. Построим логическую схему.
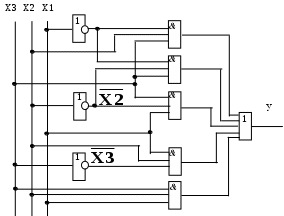
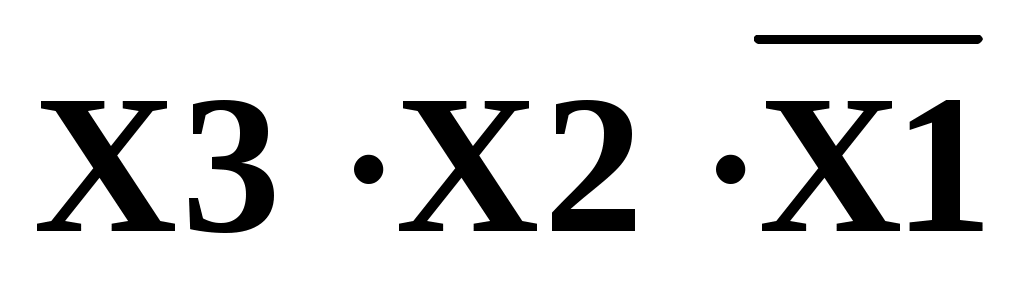
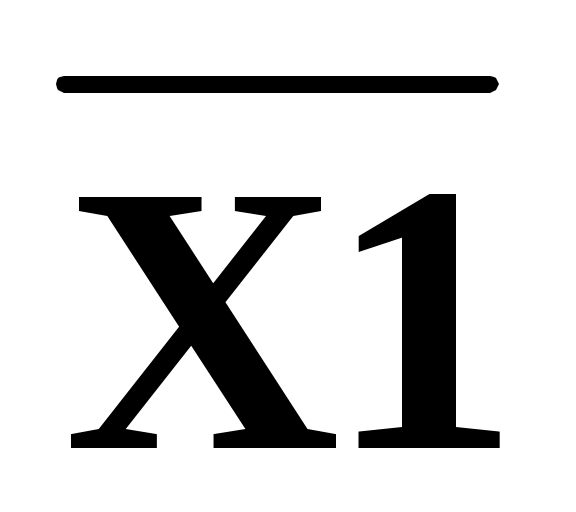
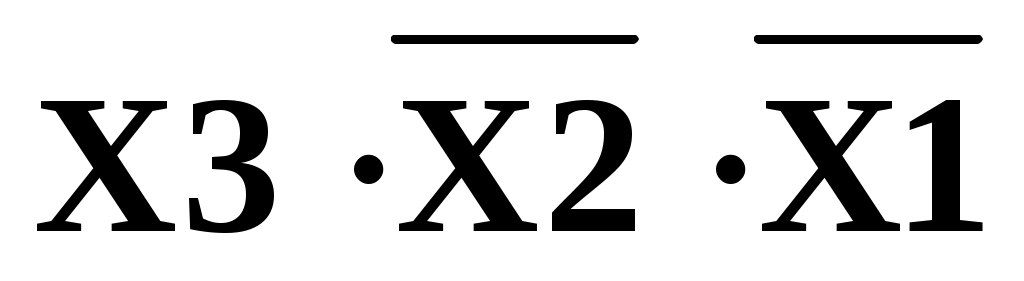
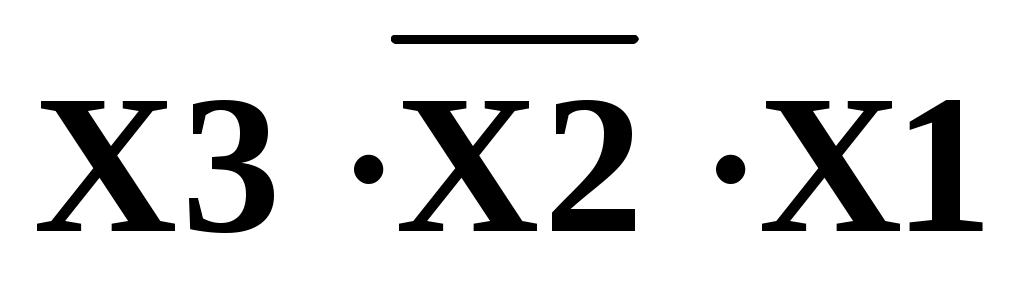
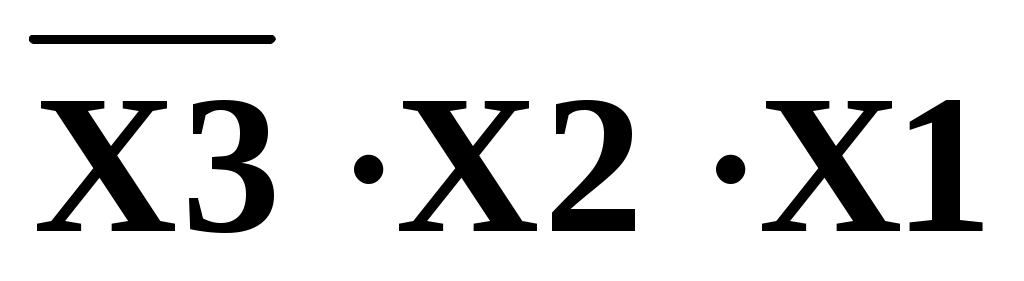
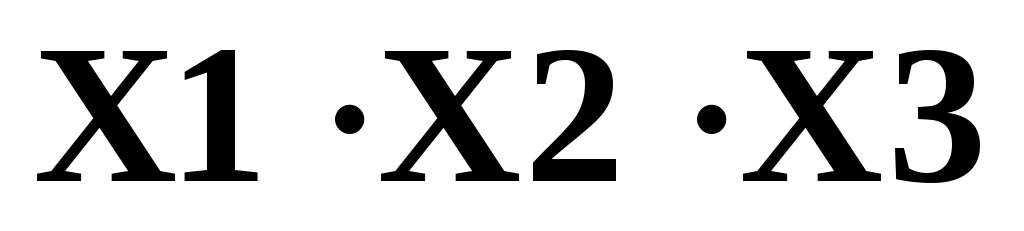
Рисунок 21 Логическая схема ЦУ
Построенная таким образом схема обеспечит правильное функционирование устройства. Однако, сама схема ЦУ получается сложной и громоздкой, т.к. содержит большое количество элементов. Затраты на построение таких схем увеличиваются, а надежность схем уменьшается.
Эти недостатки ЦУ устраняются за счет упрощения исходных логических выражений, представленных в форме СНДФ, СНКФ. При этом закон функционирования самого ЦУ не изменяется.
Процесс упрощения логических выражений называется минимизацией.
Основная задача минимизации заключается в получении минимальной формы логической функции. В результате получается логическая схема, содержащая наименьшее число логических элементов, что снижает стоимость схемы ЦУ.
Существует несколько способов минимизации. Все они базируются на применении основных законов теорем и тождеств алгебры логики:
1.4.4 Минимизация логических функций табличным методом
Данный метод также называется методом Вейча-Карно. Табличный способ минимизации является графическим и самым наглядным. Он применяется для минимизации логических функций, образованных от небольшого количества аргументов. Для минимизации применяется специальная таблица, называемая диаграммой Вейча или картой Карно. Она представляет собой своеобразную запись таблицы истинности цифрового устройства.
Количество клеток диаграммы зависит от количества аргументов, образующих функцию и определяется по формуле:
N=2n , где n количество аргументов Х
N количество клеток таблицы.
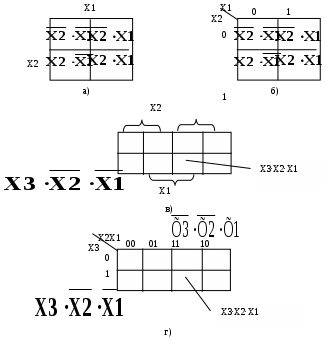
Рисунок 22: а)-б) шаблон диаграммы Вейча и карты Карно для 2-х аргументов СНДФ в)-г) шаблон диаграммы Вейча и карты Карно для 3-х аргументов СНДФ
Соответственно для двух аргументов Х1 и Х2 диаграмма будет иметь N=22 =4 клетки, для трех аргументов (Х1, Х2, Х3) N=8 клеток, для четырех аргументов (Х1, Х2, Х3, Х4) N=16 клеток.
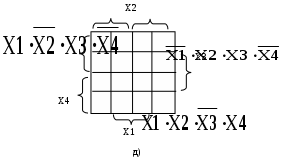
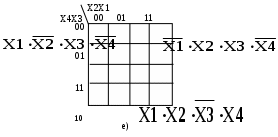
Рисунок 22 - д)-е) шаблон диаграммы Вейча и карты Карно для 4-х аргументов СНДФ
Каждой клетке диаграммы или карты Карно соответствует один набор аргументов логической функции (минтерм). Если значение функции на данном наборе равно единице «1», то клетка заполняется единицей «1». В этом случае функция представлена в форме СНДФ.
Если функция представлена в форме СНКФ, то клетки заполняются нулями «0».
Нужная клетка диаграммы или карты определяется по значению, двоичному номеру, набора аргументов логической функции. Она находится на пересечении строк и столбцов, принадлежащих соответствующим аргументам. Причем, если функция задана в форме СНДФ, то аргумент Х=1, аргумент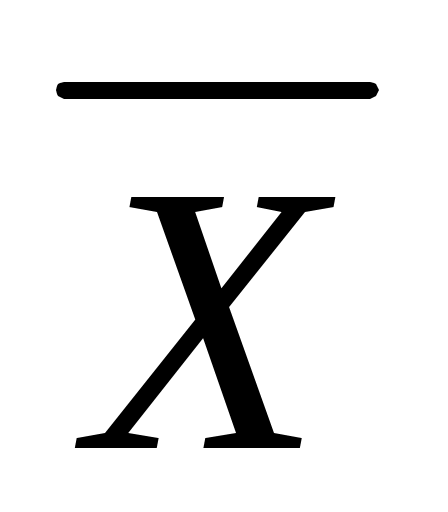 =0.
=0.
Для формы СНКФ аргумент Х=0, аргумент =1.
=1.
В диаграмме Вейча и карте Карно соседними следует считать такие клетки, которые располагаются рядом в каждом столбце (по вертикали) и каждой строке (по горизонтали), а также крайние клетки каждого столбца и каждой строки (если сворачивать диаграмму в цилиндр).
Любые две соседние в строке или столбце клетки склеиваются по соответствующей переменной между собой. В результате склеивания исключается та переменная, значение которой меняется.
Для того, чтобы выполнить минимизацию логической функции методом Вейча, необходимо:
Пример 1: Пусть функция задана таблицей истинности (таблица 22). Согласно таблице запишем логическую функцию в виде СНДФ. Дизъюнктивная форма записывается по значению функции У=1, в виде дизъюнкции простых конъюнкций.
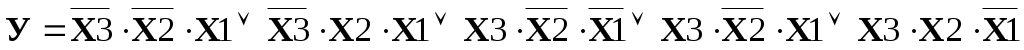

Таблица 22 - Таблица истинности логической функции
Так как функция образована от трех аргументов, то диаграмма (карта) будет содержать восемь клеток.
Диаграмму и карту Карно легче заполнить, если каждый минтерм представить в виде номера набора и найти для него соответствующую клетку.
Тогда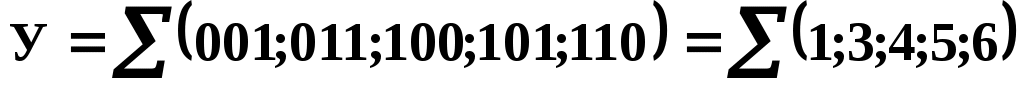
Заполняем карту Карно в соответствии с рисунком 3 и таблицей 2, и объединяем клетки в группы по вышеуказанным правилам (рисунок 4). Записываем минимальную форму логической функции (МДФ).
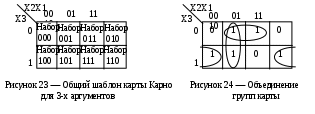
Записываем минимальную форму логической функции (МДФ).
Для крайних угловых клеток карты импликанта равна: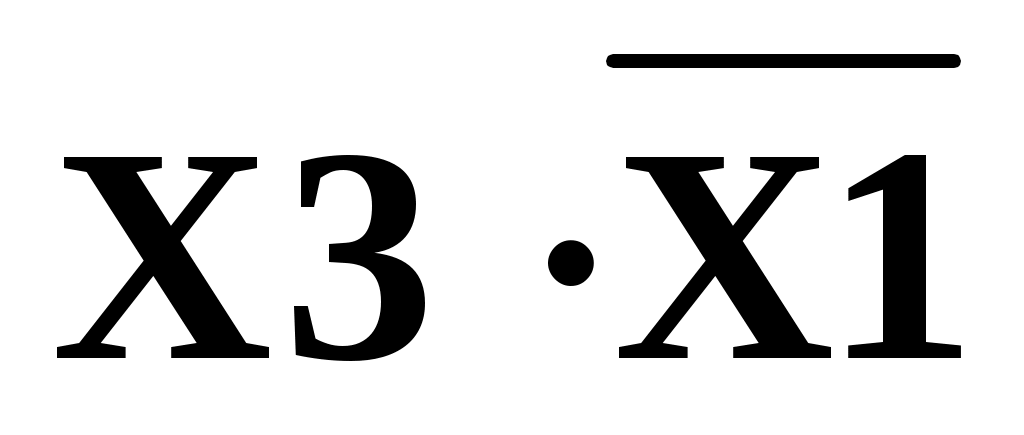
Эта группа занимает одну строку, в которой находится элемент Х3=1 и два столбца, в которых: 1) Х2=0, Х1=0
Так как значения (т.е. «0» и «1») Х2 различны, то по теореме склеивания аргумент Х2 исключается, остается Х1.
Ответ записывается в виде простой конъюнкции, значение которой в каждой клетке данной группы равны .
.
Группа, располагаемая вертикально, занимает один столбец, в котором: Х2=0, Х1=1 и две строки, в которых Х3=0 и Х3=1.
Склеивание происходит по аргументу Х3, остается: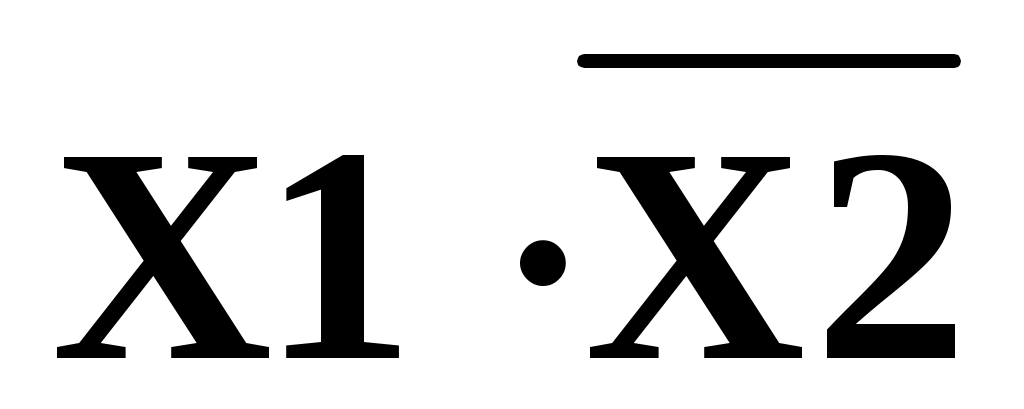 .
.
Группа, располагаемая горизонтально, занимает одну строку, в которой Х3=0 и два столбца.
В первом Х1=1, Х2=0, во втором Х1=1, Х2=1.
Склеивание происходит по аргументу Х2, остается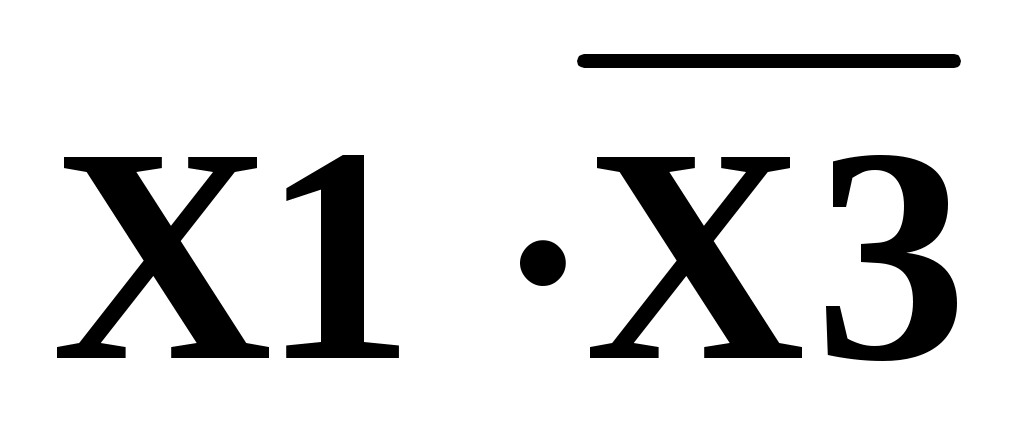 .
.
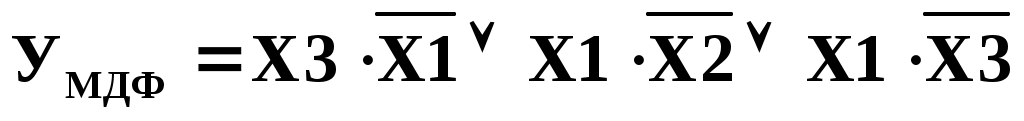
Пример 2: функция задана в СНКФ
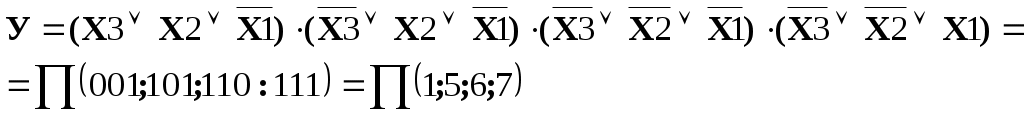
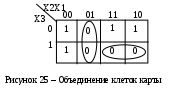
Карта Карно данной функции приведена на рисунке 5. Объединение клеток производится по нулевым значениям функции в соответствии с вышеуказанными правилами.
Вертикальная группа занимает один столбец, в котором Х2=0, Х1=1 и две строки. В них Х3=0 и Х3=1. Склеивание происходит по Х3. Простая имплианта для этой группы равна: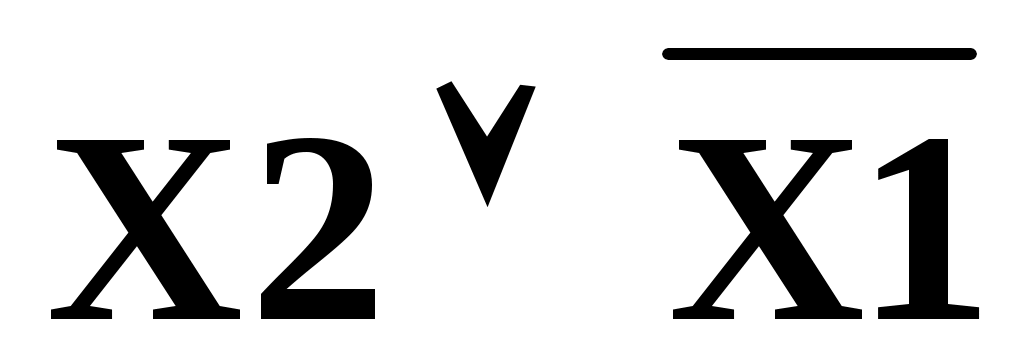 .
.
Горизонтальная группа занимает два столбца и одну строку. В первом столбце: Х2=1,Х1=1. Во втором: Х2=1, Х1=0. Склеивание происходит по Х1. В строке находится аргумент Х3=1. Простая импликанта равна: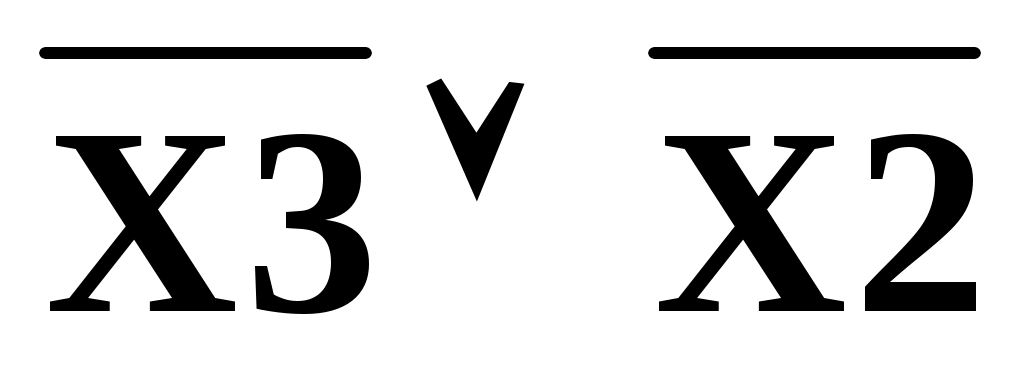 .
.
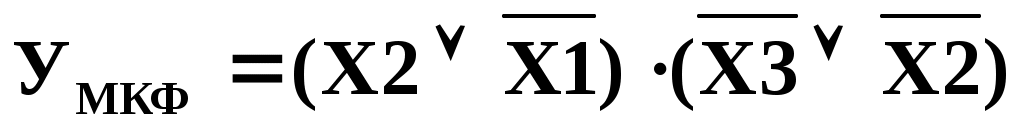
Пример 3: Минимизировать функцию, представленную в форме СНДФ табличным способом.

Данная функция образована от количества аргументов, равным четырем. Поэтому карта Карно будет иметь 16 клеток. Заполнение карты производится по заданным наборам логической функции. Так как функция представлена в форме СНДФ, то в клетках карты на заданных наборах будут находиться «1», а в остальных клетках «0».
Минимизация карты производится по вышеуказанным правилам.
Пример 3:
а) НДФ
б) НКФ
В примере 3 а) в первой простой конъюнкции отсутствует прямое значение аргумента Х1 или его инверсии;
В примере 3 б) во второй простой конъюнкции отсутствует значение аргумента Х3 или его инверсия.
В следующих двух выражениях функция не является нормальной и совершенной. Функция ДФ несовершенна, так как в первой простой конъюнкции отсутствует значение аргумента Х3 или его инверсия. Нормальный вид функции ДФ нарушает второе значение аргумента Х1 в первой простой конъюнкции и значение
Совершенный вид функции КФ нарушает отсутствие значений Х1, Х3 и их инверсии в первой простой дизъюнкции, а также отсутствие значений Х1, Х2 и их инверсии на месте третьей простой дизъюнкции. Функция не является нормальной, так как на месте первой простой дизъюнкции приведены два одинаковых значения аргументов Х2.
ДФ
К

Ф
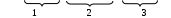
Цифровой способ записи позволяет получить компактное логическое выражение, в котором присутствуют номера наборов аргументов.
Для функции СНДФ под знаком суммы перечисляются номера наборов (в порядке возрастания), на которых функция принимает значение «1».
Все оставшиеся наборы функции (таблица 1) будут записываться под знаком произведения. На основании такой записи можно легко перейти к алгебраической записи логической функции.
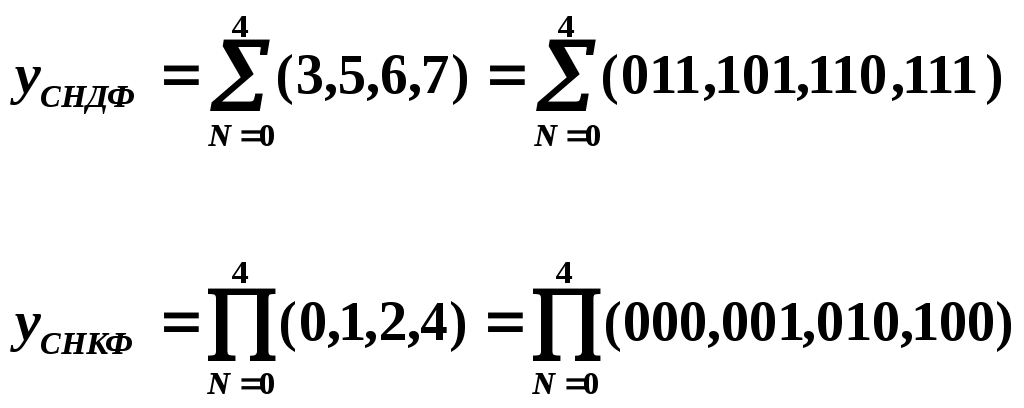
1.4.3 МИНИМИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
Общие сведения
Для того, чтобы построить логическую схему любого цифрового устройства, достаточно записать его логическую функцию в виде СНДФ или СНКФ, а затем реализовать ее с помощью простейших логических элементов.
Пример1: Логическая функция задана в форме СНДФ
АНАЛИЗ. Для реализации схемы согласно выражения необходимо использовать 9 элементов:
3 элемента НЕ,
5 элементов 3И,
1 элемент 5ИЛ.
СИНТЕЗ. Построим логическую схему.

Рисунок 21 Логическая схема ЦУ
Построенная таким образом схема обеспечит правильное функционирование устройства. Однако, сама схема ЦУ получается сложной и громоздкой, т.к. содержит большое количество элементов. Затраты на построение таких схем увеличиваются, а надежность схем уменьшается.
Эти недостатки ЦУ устраняются за счет упрощения исходных логических выражений, представленных в форме СНДФ, СНКФ. При этом закон функционирования самого ЦУ не изменяется.
Процесс упрощения логических выражений называется минимизацией.
Основная задача минимизации заключается в получении минимальной формы логической функции. В результате получается логическая схема, содержащая наименьшее число логических элементов, что снижает стоимость схемы ЦУ.
Существует несколько способов минимизации. Все они базируются на применении основных законов теорем и тождеств алгебры логики:
-
расчетный -
расчетно-табличный -
табличный
1.4.4 Минимизация логических функций табличным методом
Данный метод также называется методом Вейча-Карно. Табличный способ минимизации является графическим и самым наглядным. Он применяется для минимизации логических функций, образованных от небольшого количества аргументов. Для минимизации применяется специальная таблица, называемая диаграммой Вейча или картой Карно. Она представляет собой своеобразную запись таблицы истинности цифрового устройства.
Количество клеток диаграммы зависит от количества аргументов, образующих функцию и определяется по формуле:
N=2n , где n количество аргументов Х
N количество клеток таблицы.

Рисунок 22: а)-б) шаблон диаграммы Вейча и карты Карно для 2-х аргументов СНДФ в)-г) шаблон диаграммы Вейча и карты Карно для 3-х аргументов СНДФ
Соответственно для двух аргументов Х1 и Х2 диаграмма будет иметь N=22 =4 клетки, для трех аргументов (Х1, Х2, Х3) N=8 клеток, для четырех аргументов (Х1, Х2, Х3, Х4) N=16 клеток.

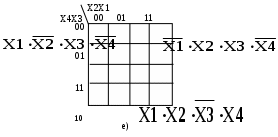
Рисунок 22 - д)-е) шаблон диаграммы Вейча и карты Карно для 4-х аргументов СНДФ
Каждой клетке диаграммы или карты Карно соответствует один набор аргументов логической функции (минтерм). Если значение функции на данном наборе равно единице «1», то клетка заполняется единицей «1». В этом случае функция представлена в форме СНДФ.
Если функция представлена в форме СНКФ, то клетки заполняются нулями «0».
Нужная клетка диаграммы или карты определяется по значению, двоичному номеру, набора аргументов логической функции. Она находится на пересечении строк и столбцов, принадлежащих соответствующим аргументам. Причем, если функция задана в форме СНДФ, то аргумент Х=1, аргумент
Для формы СНКФ аргумент Х=0, аргумент
В диаграмме Вейча и карте Карно соседними следует считать такие клетки, которые располагаются рядом в каждом столбце (по вертикали) и каждой строке (по горизонтали), а также крайние клетки каждого столбца и каждой строки (если сворачивать диаграмму в цилиндр).
Любые две соседние в строке или столбце клетки склеиваются по соответствующей переменной между собой. В результате склеивания исключается та переменная, значение которой меняется.
Для того, чтобы выполнить минимизацию логической функции методом Вейча, необходимо:
-
Заполнить диаграмму (карту). Это значит отметить «1» и «0» те клетки, которые соответствуют минтермам, образующим функцию. -
Отмеченные на диаграмме клетки сгруппировать. Группировать можно только соседние клетки. При этом количество групп должно быть минимальным, а количество клеток в группе максимальным и равным целой степени двух: две (21=2), четыре (22=4), восемь (23=8), шестнадцать (24=16). -
Одни и те же клетки могут входить в несколько групп с условием, что они сгруппированы по вышеуказанным правилам. -
Минимальная форма записывается в виде простых импликант (результата склеивания) для каждой объединенной группы минтермов.
Пример 1: Пусть функция задана таблицей истинности (таблица 22). Согласно таблице запишем логическую функцию в виде СНДФ. Дизъюнктивная форма записывается по значению функции У=1, в виде дизъюнкции простых конъюнкций.

Таблица 22 - Таблица истинности логической функции
| № набора | Х3 | Х2 | Х1 | У |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 2 | 0 | 1 | 0 | 0 |
| 3 | 0 | 1 | 1 | 1 |
| 4 | 1 | 0 | 0 | 1 |
| 5 | 1 | 0 | 1 | 1 |
| 6 | 1 | 1 | 0 | 1 |
| 7 | 1 | 1 | 1 | 0 |
Так как функция образована от трех аргументов, то диаграмма (карта) будет содержать восемь клеток.
Диаграмму и карту Карно легче заполнить, если каждый минтерм представить в виде номера набора и найти для него соответствующую клетку.
Тогда
Заполняем карту Карно в соответствии с рисунком 3 и таблицей 2, и объединяем клетки в группы по вышеуказанным правилам (рисунок 4). Записываем минимальную форму логической функции (МДФ).

Записываем минимальную форму логической функции (МДФ).
Для крайних угловых клеток карты импликанта равна:
Эта группа занимает одну строку, в которой находится элемент Х3=1 и два столбца, в которых: 1) Х2=0, Х1=0
-
Х2=1,Х1=0.
Так как значения (т.е. «0» и «1») Х2 различны, то по теореме склеивания аргумент Х2 исключается, остается Х1.
Ответ записывается в виде простой конъюнкции, значение которой в каждой клетке данной группы равны
Группа, располагаемая вертикально, занимает один столбец, в котором: Х2=0, Х1=1 и две строки, в которых Х3=0 и Х3=1.
Склеивание происходит по аргументу Х3, остается:
Группа, располагаемая горизонтально, занимает одну строку, в которой Х3=0 и два столбца.
В первом Х1=1, Х2=0, во втором Х1=1, Х2=1.
Склеивание происходит по аргументу Х2, остается
Пример 2: функция задана в СНКФ
Карта Карно данной функции приведена на рисунке 5. Объединение клеток производится по нулевым значениям функции в соответствии с вышеуказанными правилами.

Вертикальная группа занимает один столбец, в котором Х2=0, Х1=1 и две строки. В них Х3=0 и Х3=1. Склеивание происходит по Х3. Простая имплианта для этой группы равна:
Горизонтальная группа занимает два столбца и одну строку. В первом столбце: Х2=1,Х1=1. Во втором: Х2=1, Х1=0. Склеивание происходит по Х1. В строке находится аргумент Х3=1. Простая импликанта равна:
Пример 3: Минимизировать функцию, представленную в форме СНДФ табличным способом.

Данная функция образована от количества аргументов, равным четырем. Поэтому карта Карно будет иметь 16 клеток. Заполнение карты производится по заданным наборам логической функции. Так как функция представлена в форме СНДФ, то в клетках карты на заданных наборах будут находиться «1», а в остальных клетках «0».
Минимизация карты производится по вышеуказанным правилам.