Файл: Протокол 1 от 28 августа 2020 г. Конспект лекций содержание введение Краткая характеристика дисциплины.doc

- элементов И—НЕ (элементов Шеффера) в базисе И—НЕ

- элементов ИЛИ—НЕ(элементов Пирса) в базисе ИЛИ—НЕ

Функция инверсии в данных базисах реализуется как показано на рисунке 1б) и 1в).
СИНТЕЗ КЦУ В БАЗИСЕ ИЛИ—НЕ
Синтезируем логическое устройство на Примере 7

Запишем логическую функцию через операцию ИЛИ—НЕ. Для этого воспользуемся основными правилами перевода: законом двойного отрицания и теоремой Моргана.

Произведем анализ логического выражения.

Для построения схемы логического устройства в базисе ИЛИ—НЕ необходимо:

1 Выполнить инверсию аргументов Х2 и Х3. Для этого используем два элемента ИЛИ—НЕ (рисунок 1в) ;

2 Две группы аргументов (то что в скобках) получаем с помощью двух элементов ИЛИ--НЕ на два входа;

3 Для реализации логической функции «У» используем один элемент ИЛИ—НЕ на два входа.

Строим схему логического устройства согласно выражения базиса ИЛИ—НЕ и производим выбор микросхем.



Рисунок 31  Логическая схема ЦУ в базисе ИЛИ--НЕ

В данной схеме использован 2 ИМС К176ЛЕ5 DD1.1—DD1.4, DD2.1.

Микросхема К176ЛЕ5 содержит 4 элемента ИЛИ--НЕ. . Для построения данной схемы используются все элементы одной микросхемы DD1 и 1 элемент из 3 микросхемы DD2.

Схема будет более рациональной (Рисунок 12), если при ее построении использовать микросхему с трехвходовыми логическими элементами К176ЛЕ10. Она содержит три трехвходовых элемента ИЛИ—НЕ. Для построения данной схемы используется полностью одна и 2 / 3 микросхемы К176ЛЕ10 (DD1и DD2).


Х3 Х2 Х1

0 0 1




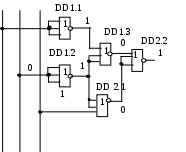
Рисунок 32  Принципиальная электрическая схема в базисе ИЛИ--НЕ
СИНТЕЗ КЦУ В БАЗИСЕ И—НЕ
На Примере 8 запишем логическую функцию через операцию И—НЕ.

Для перевода в базис применяем закон двойного отрициния к логическому выражению У.

Нижний знак инверсии и знак конъюнкции между скобками заменяем на «штрих Шеффера», при этом значение логического выражения будет инверсным.

---

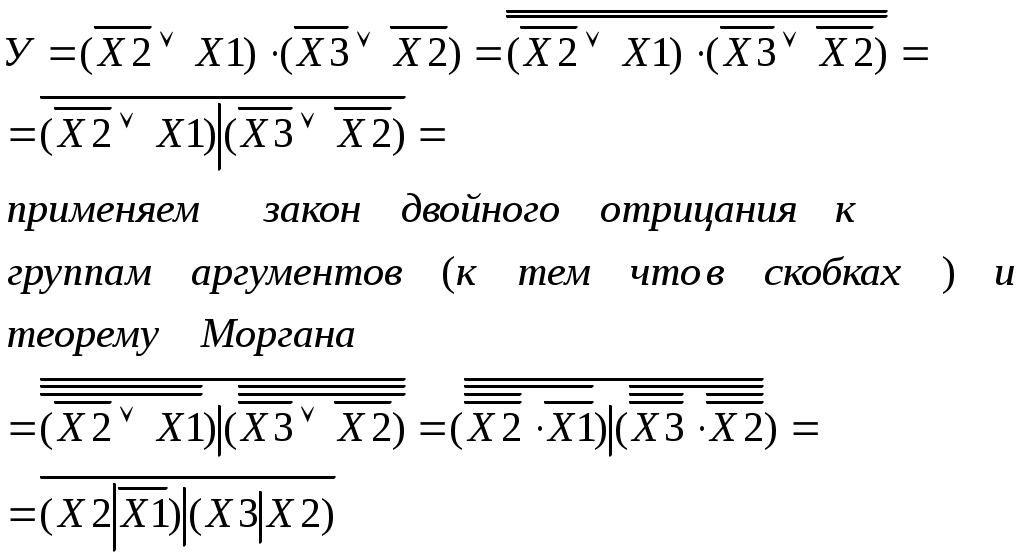
Произведем анализ этого выражения.

Для построения схемы логического устройства в базисе

И—НЕ необходимо:

1 Выполнить инверсию аргумента Х1. Для этого используется элемент И—НЕ (рисунок 1б);

2 Две группы аргументов (то что в скобках) получаем с помощью двух элементов И--НЕ на два входа;



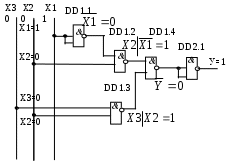
X1=1


Рисунок 33  Логическая схема ЦУ в базисе И—НЕ
Для получения прямого значения функции У используем один элемент И—НЕ на два входа;

Для рализации инверсного значения функции У также используем один элемент И—НЕ на два входа.

Строим схему логического устройства (рисунок 13) согласно выражения базиса И—НЕ и производим выбор микросхем.

В данной схеме использовано 2 ИМС К155ЛА3 DD1, DD2

Микросхема К155А3 содержит 4 элемента И--НЕ. . Для построения данной схемы используются все элементы микросхемы DD1 и 1/ 4 микросхемы DD2.

Если при построении схемы использовать микросхему с трехвходовыми логическими элементами К155ЛА4, то она будет более рациональной (Рисунок 34). Микросхема К155ЛА4 содержит три трехвходовых элемента И—НЕ. Для построения данной схемы используются все элементы одной микросхемы К155ЛА4 и 2 / 3 микросхемы К155ЛА4 (DD1и DD2).


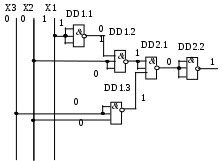
Рисунок 34  Принципиальная электрическая схема в базисе И--НЕ

---

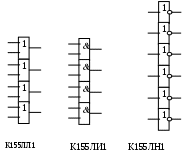
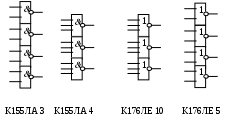
ПРИЛОЖЕНИЕ

Рисунок 35—УГО микросхем

РАЗДЕЛ 2 ЦИФРОВЫЕ УСТРОЙСТВА
2.1 Типовые КЦУ
2.1.1 ШИФРАТОРЫ
Шифратор (CD– называемый также кодером) – устройство, осуществляющее преобразование десятичных чисел в двоичную систему счисления. Шифратор имеет mвходов, последовательно пронумерованных десятичными числами и n выходов. Подача сигнала на один из входов приводит к появлению на выходах n-разрядного двоичного кода, соответствующего номеру возбуждённого входа.

Шифраторы широко применяются в различных устройствах ввода информации. Они обычно снабжаются клавиатурой, клавиши которой в исходном состоянии отжаты. При нажатии одной из клавиш, на выходе дешифратора появляется двоичный код, соответствующий символу, изображенному на клавиатуре.

Условно-графическое изображение шифратора приведено на рисунке 1.


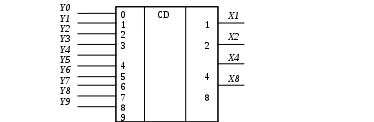
Рисунок 1 – УГО шифратора
Слева показаны 10 входов, обозначенных десятичными цифрами 0, 1. . . 9. Справа показаны выходы шифратора; цифрами 1, 2, 4, 8 обозначены весовые коэффициенты двоичных разрядов, соответствующих отдельным выходам. Таблица истинности шифратора имеет вид.


Таблица 1 - Таблица истинности шифратора

Десятичное число	Двоичный код
	X8	X4	X2	X1
0	0	0	0	0
1	0	0	0	1
2	0	0	1	0
3	0	0	1	1
4	0	1	0	0
5	0	1	0	1
6	0	1	1	0
7	0	1	1	1
8	1	0	0	0
9	1	0	0	1

---

По таблице истинности для каждого выхода запишем логическую функцию.


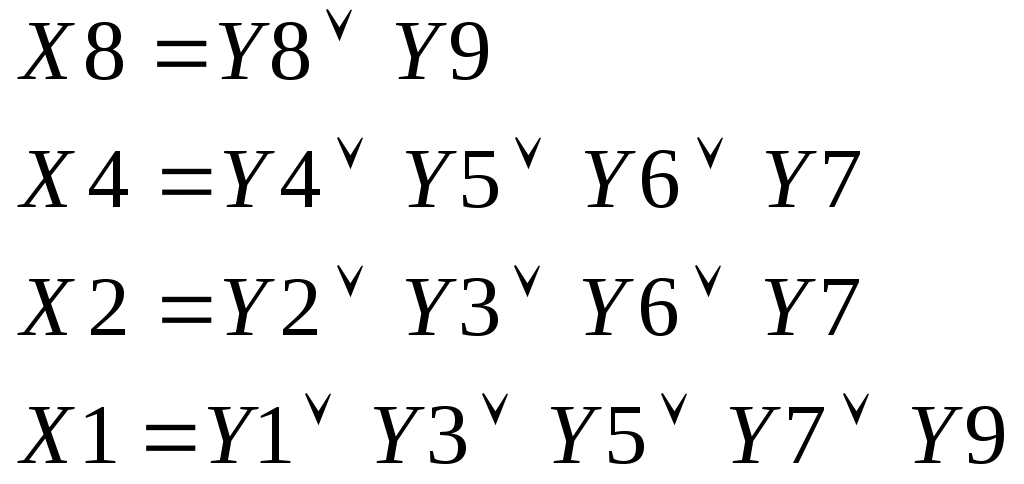
Построим схему в базисе «И, ИЛИ, НЕ»


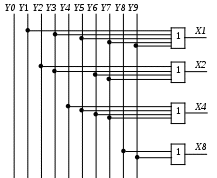
Рисунок 2 – Структурная схема шифратора
Выполним перевод полученных логических выражений в базис «И-НЕ»:





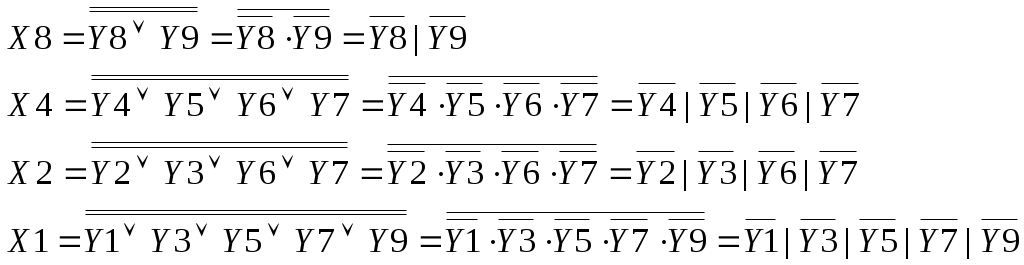
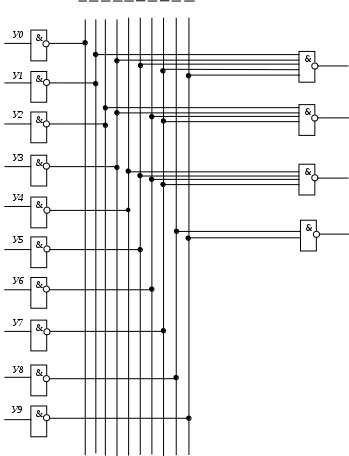
У0 У1 У2 У3 У4 У5 У6 У7 У8 У9

X1

X2

X4

X8


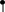
Рисунок 3 – Логическая схема шифратора в базисе «И – НЕ»
Логическая схема шифратора приведенная на рисунке 3.


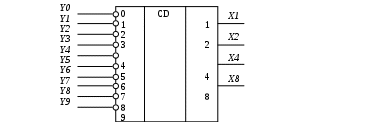
Рисунок 4 – УГО шифратора в базисе «И – НЕ»
Активным сигналом на входе будет «0».

Запишем логические выражения для выходов шифратора в базисе «ИЛИ – НЕ»:

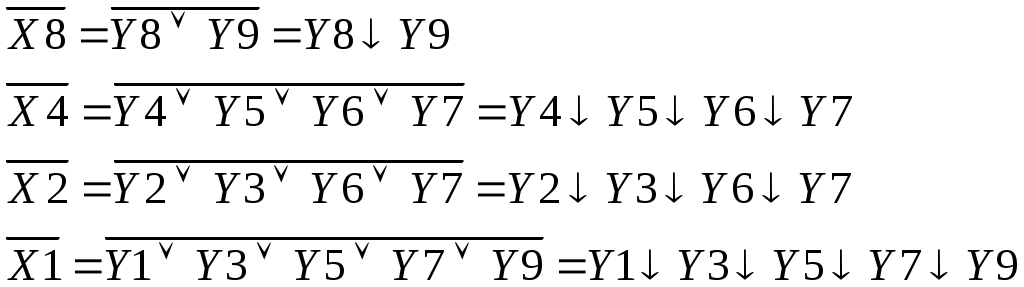
УГО шифратора в базисе «ИЛИ – НЕ» имеет инверсные выходы (Х1, Х2, Х4, Х8). Активный сигнал на выходах соответствует «0» (на входе – «1»).

---

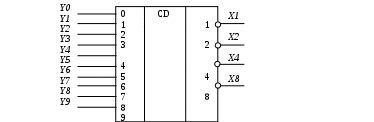
Рисунок 5 – УГО шифратора в базисе «ИЛИ – НЕ»

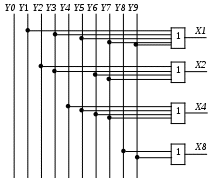
Рисунок 6 – Логическая схема шифратора в базисе «ИЛИ – НЕ»

2.1.2 ДЕШИФРАТОРЫ
Дешифраторы (DC – называемый также декодером) – это КЦУ, предназначенное для обратного преобразования двоичного кода в единичный сигнал и выдачу его на одном определённом выходе, соответствующем двоичному коду, поступившему на вход.

Дешифраторы широко применяются в различных устройствах компьютеров. Прежде всего, они используются в устройствах, печатающих на бумаге выводимые из цифрового устройства числа или текст. В таких устройствах двоичное число, поступая на вход дешифратора, вызывает появление сигнала на определённом его выходе. С помощью этого сигнала производится печать символа, соответствующего входному двоичному числу.

На рисунке 7 приведено символическое изображение дешифратора.



Рисунок 7 – УГО дешифратора
Составим таблицу истинности дешифратора.

Таблица 2 - Таблица истинности DC

Входы				Выходы
Х8	Х4	Х2	Х1	Y0	Y1	Y2	Y3	Y4	Y5	Y6	Y7	Y8	Y9
0	0	0	0	1	0	0	0	0	0	0	0	0	0
0	0	0	1	0	1	0	0	0	0	0	0	0	0
0	0	1	0	0	0	1	0	0	0	0	0	0	0
0	0	1	1	0	0	0	1	0	0	0	0	0	0
0	1	0	0	0	0	0	0	1	0	0	0	0	0
0	1	0	1	0	0	0	0	0	1	0	0	0	0
0	1	1	0	0	0	0	0	0	0	1	0	0	0
0	1	1	1	0	0	0	0	0	0	0	1	0	0
1	0	0	0	0	0	0	0	0	0	0	0	1	0
1	0	0	1	0	0	0	0	0	0	0	0	0	1

---