Файл: Протокол 1 от 28 августа 2020 г. Конспект лекций содержание введение Краткая характеристика дисциплины.doc

Согласно таблице 1 запишем логически выражения для выходов DC:







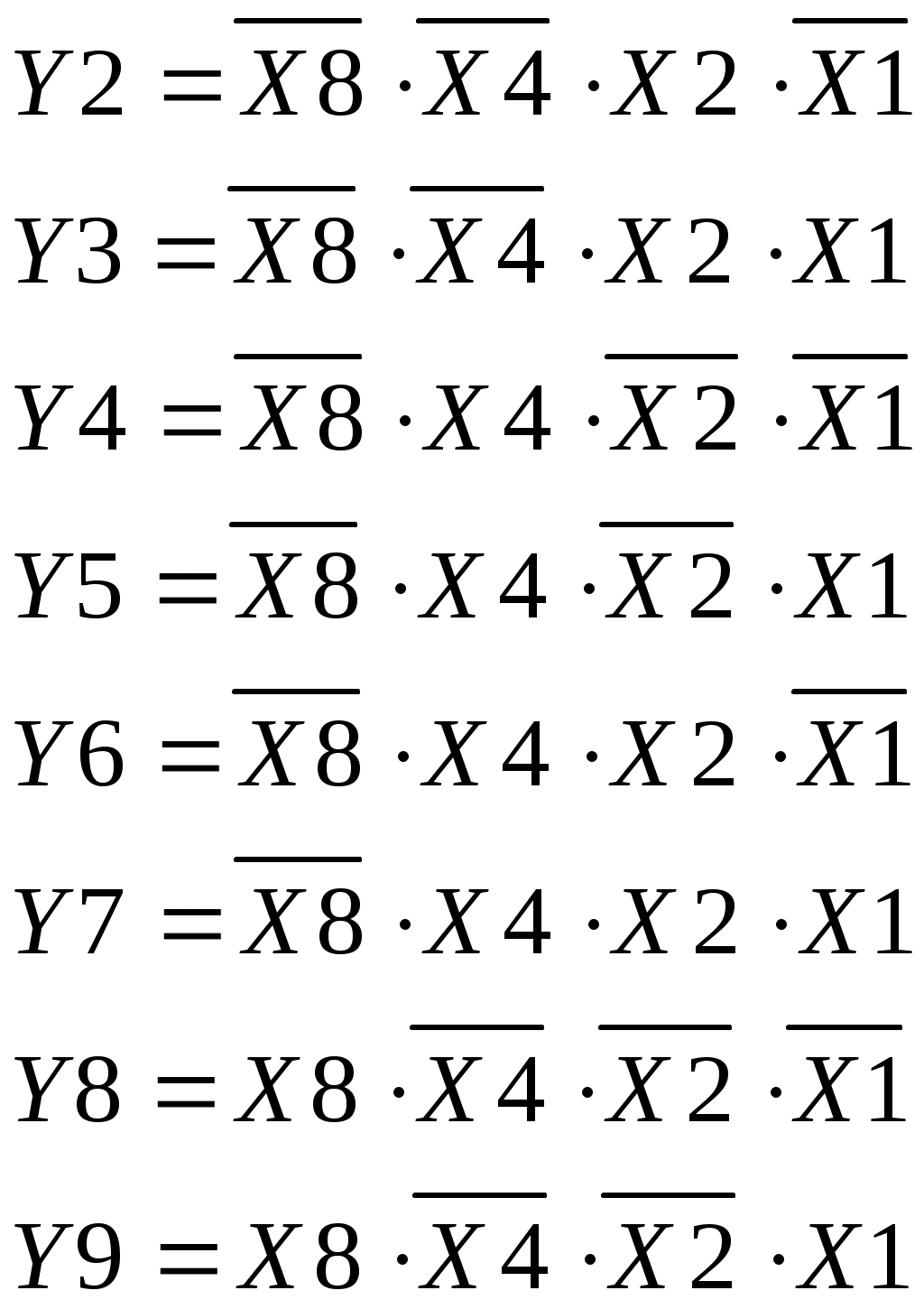
Построим схему DC в базисе «И, ИЛИ, НE».



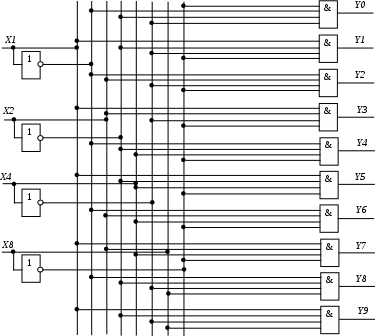
Рисунок 8 - Структурная схема дешифратора

Переведём логические выражения для выходов (Y) в базис «И-НЕ».

В этом случае Y - инверсные («0»).




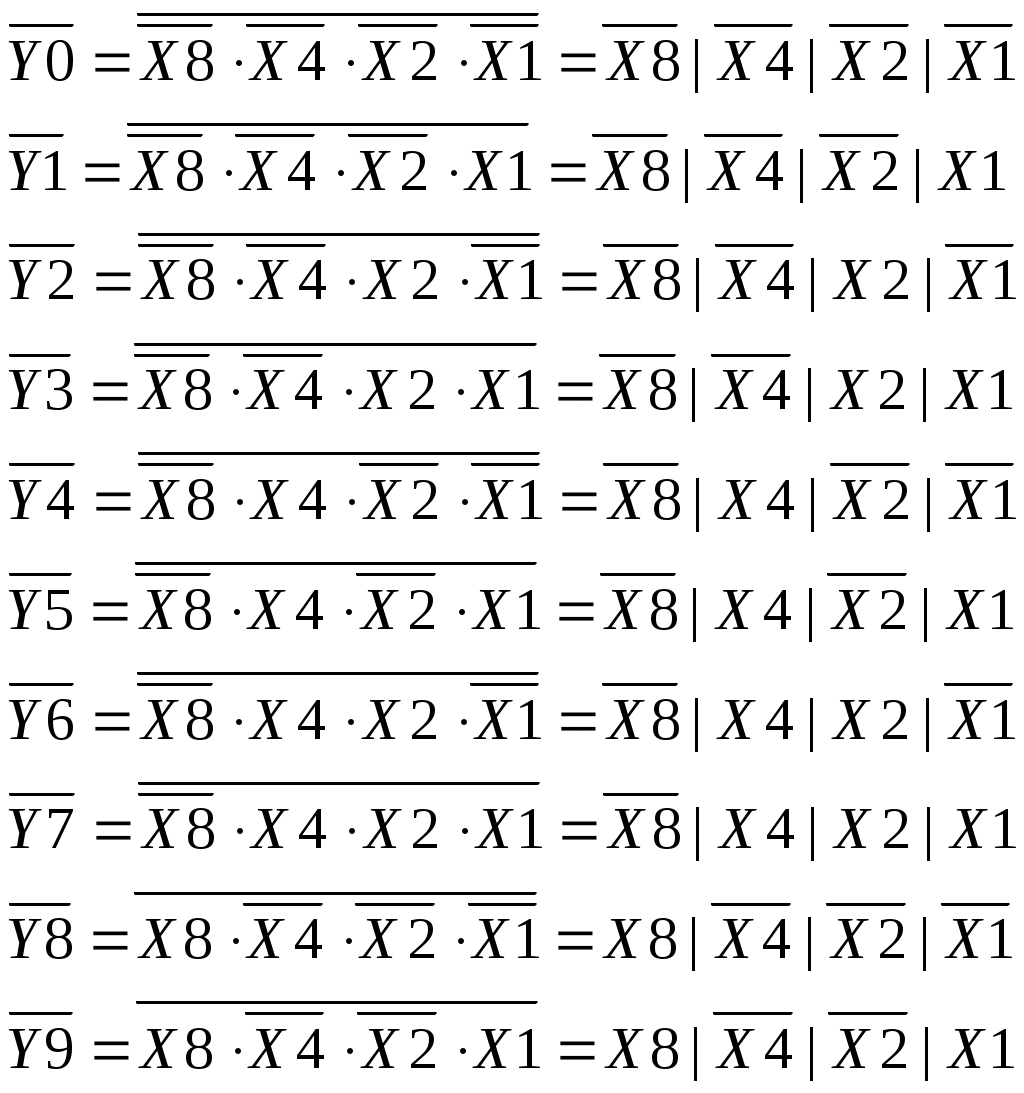
Рисунок 9 - УГО DC в базисе «И-НЕ»
Активный сигнал на выходе - «0»

---

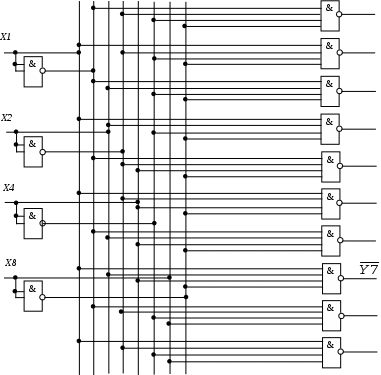
Рисунок 10 - Структурная схема DC в базисе «И-НЕ»
Запишем логические выражения для выходов DC в базисе «ИЛИ-НЕ»



















УГО DC базиса «ИЛИ-НЕ» имеет инверсные входы (Х). Активный сигнал для входа «0». Выходы (У) прямые.



Рисунок 11 - УГО DC базиса «ИЛИ-НЕ»






























Рисунок 12 - Структурная схема DC в базисе «ИЛИ-НЕ»

---

2.1.3 МУЛЬТИПЛЕКСОРЫ
Мультиплексор (MS) - это КЦУ, предназначенное для выбора и подключения одного из информационных входов к своему выходу.

Мультиплексор (MS) - имеет несколько информационных входов (D); несколько адресных входов (А) и один выход.

В соответствии с кодом на входах «А» выбирается и подключается соответствующий вход D. Каждый информационный вход (D) имеет свой адрес (А).

Зависимость между входами А и D MS:

,

где А-количество адресных входов

D - количество информационных входов.

УГО мультиплексора:


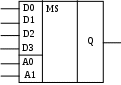
Рисунок 13 - УГО ИМС MS
Составляем таблицу истинности MS:

Таблица 3 – Таблица истинности MS

Входы		Выходы
А1	А0	Q
0	0	D0
0	1	D1
1	0	D2
1	1	D3

Запишем по таблице истинности логическое выражение для MS:



Построим схему мультиплексора согласно логическому выражению:


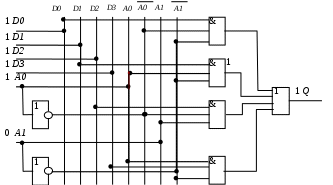
Рисунок 14 - Логическая схема MS
Объединив между собой несколько MS можно получить мультиплексное устройство (дерево). Объединение 2-х устройств (MS и DM) в одно создает коммутатор.

2.1.4 ДЕМУЛЬТИПЛЕКСОРЫ
Демультиплексор (DM) - цифровое устройство, осуществляющее распределение сигналов, поступающих на его единственный информационный вход D, на один из нескольких выходов Q₀ – Q_n. Номер выхода Q_n, подключаемого ко входу D, определяется двоичным кодом, поданным на адресные входы А₀ – А_n.

При наличии в схеме демультиплексора входа синхронизации С, подключение выхода ко входу происходит только при наличии на входе С активного сигнала.

Соотношение между количеством выходов Q

---

_n и числом адресных входов А_n определяется формулой:

Q=2^А
Где А - количество адресных входов DM

Q – количество выходов DM





Рисунок 15 – УГО ИМС DM
Таблица 4 – Таблица истинности DM

Входы		Выходы
А1	А0	Q0	Q1	Q2	Q3
0	0	D	0	0	0
0	1	0	D	0	0
1	0	0	0	D	0
1	1	0	0	0	D

Запишем логические выражения для выходов Q



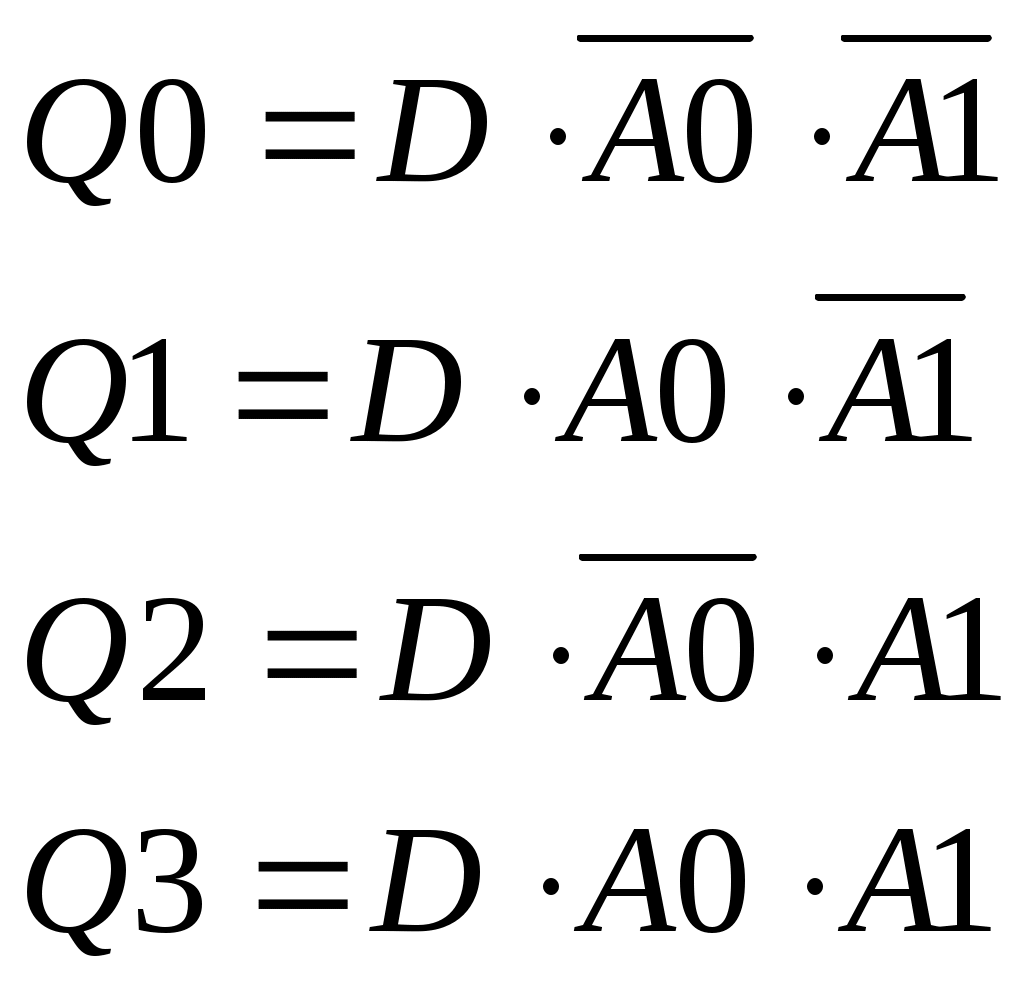
Построим логическую схему демультиплексора:



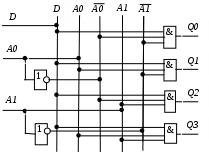
Рисунок 16 –Логическая схемаDM

2.1.5 КОДОПРЕОБРАЗОВАТЕЛИ
В линиях связи информация передается в кодированном виде. Существует множество кодов 8421; 2421; 7421; с избытком 3 и т. п.

В некоторых случаях возникает необходимость преобразования одного кода в другой. Эту задачу выполняют кодопреобразователи (КП).

К кодопреобразователям так же относятся 7-сегментный цифровой индикатор, который позволяет отобразить любую десятичную цифру с помощью 7-сегментов (горит - «1», не горит -«0»).

Преобразование (2-10) кода в код 7-сегментного индикатора показан в таблице 5.

У1

У6

У7

У2

У5

У3

У4

---

Таблица 5 – Преобразование кода

Цифра	Двоичный код				Семисегментный код
	Х8	Х4	Х2	Х1	У1	У2	У3	У4	У5	У6	У7
0	0	0	0	0	1	1	1	1	1	1	0
1	0	0	0	1	0	1	1	0	0	0	0
2	0	0	1	0	1	1	0	1	1	0	1
3	0	0	1	1	1	1	1	1	0	0	1
4	0	1	0	0	0	1	1	0	0	1	1
5	0	1	0	1	1	0	1	1	0	1	1
6	0	1	1	0	1	0	1	1	1	1	1
7	0	1	1	1	1	1	1	0	0	0	0
8	1	0	0	0	1	1	1	1	1	1	1
9	1	0	0	1	1	1	1	1	0	1	1

---