Файл: Протокол 1 от 28 августа 2020 г. Конспект лекций содержание введение Краткая характеристика дисциплины.doc

1 4 2 2 0 4

1 2 1 2

0 0 8

2

1 6

Ответ: 10111, 1001 ₍₂₎




2
x

3,6₍₁₀₎  (8) 0, 6

2
-

3 8 8

1 6 2 4 8

7 8

6 4

8

3 2

8

1 6

Ответ: 27,4631 ₍₈₎
2 3,6₍₁₀₎  (16)

2
-


x

3 16 0, 6

1 6 1 16

7 9 6

16

9 6

16

9 6

16

Ответ: 17,9999 ₍₁₆₎ 9 6
2 Перевод из любой позиционной СС в десятичную осуществляется по формуле (1) степенного ряда:

Пример:
10111, 1001 ₍₂₎  (10)

12 ⁴ + 02 ³ + 12 ² + 12 ¹ + 12 ⁰ + 12 ^-1 + 12 ^-4 = 16 + 0 + 4 + 2 + 1 + ½ + 1/16 = 23 + 0,5 +…   23,6 ₍₁₀₎
27,4631 ₍₈₎  (10)
28

---

¹ + 78 ⁰ + 48 ^-1 + 68 ^-2 + 38 ^-3 + 18 ^-4 = 16 + 7 + 1/2 + 3/32 + …  23,6 ₍₁₀₎
17,9999 ₍₁₆₎  (10)
116 ¹ + 716 ⁰ + 916 ^-1 + 916 ^-2 + 916 ^-3 + 916 ^-4 = 16 + 7 + 9/16 + …  23,6 ₍₁₀₎
В ЦТ для физического представления чисел, подлежащих обработке, необходимы устройства, которые бы фиксировали каждую цифру в виде устойчивого состояния.

Проще всего фиксировать 2 состояния.

Поэтому с точки зрения технической реализации в ЦВМ получила наибольшее применение двоичная С.С..

Достаточно фиксировать всего 2 состояния (0 или 1).

- транзисторный ключ; ферромагнитный сердечник; реле…

1) Недостаток – число разрядов в двоичном представлении больше, чем в другой С.С..
Сравните:
10111,1001(2)  23,6000(10)  27,4631(8)  17,9999(16)
2. Недостаток – необходимость предварительного перевода исходных данных из десятичной С.С. в двоичную С.С. и обратного перевода результатов в десятичную С.С..
Представление чисел, заданных в 8, 16, 10 СС, в двоичной С.С..
Основание восьмеричной и двоичной СС связаны соответствием:

2³ = 8, поэтому каждую восьмеричную цифру можно представить трехразрядным двоичным кодом – (см. таблицу)

Таблица 1 - СС

№ п/п	Значения аргумента
	X4	X3	X2	X1
0	0	0	0	0
1	0	0	0	1
2	0	0	1	0
3	0	0	1	1
4	0	1	0	0
5	0	1	0	1
6	0	1	1	0
7	0	1	1	1
8	1	0	0	0
9	1	0	0	1
10	1	0	1	0
11	1	0	1	1
12	1	1	0	0
13	1	1	0	1
14	1	1	1	0
15	1	1	1	1

---

Основание шестнадцатеричной СС 2⁴=16, поэтому каждую шестнадцатеричную цифру можно представить четырехразрядным двоичным кодом.

Аналогично и для десятичной СС.
3 С, AF ₍₈₎ = 0011 1100, 1010 1111 ₍₂₎

3 С A F
2 4,6 ₍₈₎ = 010 100, 110 ₍₂₎

2 4 6
Обратный перевод:

Двоичное число разбивается на группы влево и вправо от запятой по 3 разряда для восьмеричной СС, и по 4 разряда для шестнадцатеричной С.С. и по таблице записывается значение цифр.

Например:

101 110 010, 000 010 01 ₍₂₎  (8) 562, 022 ₍₈₎



5 6 2 . 0 2 2 ₍₈₎
1 0111 0010, 0000 1001  (16) 172, 09 ₍₁₆₎

1 7 2 . 0 9

1.1.3 Формы представления чисел в ЭВМ
Числа в ЭВМ хранятся в памяти, память состоит из ячеек.

Одна ячейка предназначена для хранения одного машинного многоразрядного слова.

Старший разряд – знаковый.

если отрицательное число – «1»

если положительное число – «0».

Различают две формы представления чисел в ЭВМ:

- с фиксированной запятой;

- с плавающей запятой.

---

Представление чисел с фиксированной запятой:
Положение запятой строго определено:

если перед старшим разрядом – то число дробное;

если перед младшим разрядом – то число целое.



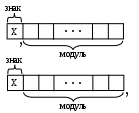
2^-1 2^-2

- дробное


2¹ 2⁰

- целое


Недостатки:

1. Переполнение – если при расчетах появились разряды числа, не помещающиеся в ячейку памяти.

2. Необходимо масштабирование исходных данных, применение специальных масштабированных коэффициентов, чтобы не было переполнения разрядной сетки.

3. Малый диапазон машинных чисел (ограничен числом разрядов в машинной сетке).
Представление чисел с плавающей запятой.
Числа представлены произведением цифровой части (мантиссы) на целую степень основания СС.

Мантисса – правильная дробь.

Например:

- 0, 624  10 ⁺³ ₍₁₀₎

+0, 01010  10 ^-101 ₍₂₎
2^-1 2^-2




2^-1 2^-2

Пример для Z = + 0, 01010  10 ^-101 ₍₂₎


0 0 1 0 1 0 …

1 1 0 1


Х Х
Обязательное условие: в памяти ЭВМ числа должны быть нормализованы, т.е. первый старший разряд = 1. В ЭВМ есть схемы нормализации, для нормализации исходных данных и промежуточных результатов.

Нормализация – сдвиг мантиссы влево до получения разряда, равного «1»
Достоинства:

- большой диапазон машинных чисел;

- высокая точность вычислений (мала абсолютная ошибка округления).

Недостатки: сложность аппаратуры, т.к. необходимо выполнить действия не только над мантиссами, но и над порядками. Необходимо наличие схемы нормализации.

Например:

- 0, 010101  10 ^-10 = - 0, 10101  10 ^-11

0, 0011101  10 ¹⁰¹ = 0, 11101  10 ¹¹
Один двоичный разряд – БИТ

---

Восьмибитовое слово – БАЙТ

ЭВМ могут перерабатывать информацию порциями – словами.

8-битовые, 16-битовые, 32-битовые;

(1, 2, 4 БАЙТ)

Вывод: В ЭВМ и ПЭВМ применяются обе формы представления чисел в соответствующих режимах работы. Они дополняют друг друга, это приводит к значительному расширению функциональных возможностей машин и систем.

1.1.4 Способы кодирования двоичных чисел в ЦТ
Во всех ЭВМ для выполнения арифметических операций над числами применяются специальные машинные коды: прямой, обратный и дополнительный. С использованием этих кодов операция вычитания (или алгебраического сложения) сводится к арифметическому суммированию, упрощается определение знака результата операции, облегчается выработка признака переполнения разрядной сетки.

В каждом из этих кодов перед старшим цифровым разрядом числа располагается знаковый разряд, в котором записывается нуль для положительного числа и единица для отрицательного. В дальнейшем при записи машинных кодов знаковый разряд будет отделяться от цифровых разрядов точкой.

Прямой код двоичного числа содержит цифровые разряды, перед которыми записан знаковый разряд. Например, для чисел х = +1101 и у = -1001 их прямые коды запишутся в виде:
х_пр = 0.1101 и у_пр = 1.1001.
Обратный код положительного числа полностью совпадает с его прямым кодом. Обратный код отрицательного числа содержит единицу в знаковом разряде, а значащие цифровые разряды числа заменяются инверсными, т.е. нули заменяются единицами, а единицы – нулями. Для приведенного выше примера с числами х и у имеем:
х_обр = 0.1101 и у_обр = 1.0110.
Особенностью обратного кода является то, что в нем нуль имеет двоякое представление. Он может быть положительным (+0)_обр = 0.00…0 и отрицательным числом (-0)_обр = 1.11…1. Двойственное представление нуля явилось причиной того, что в современных ЭВМ числа обычно представляются не обратным, а дополнительным кодом.
Дополнительный код положительного числа совпадает с прямым кодом, а для отрицательного числа образуется из обратного кода путем прибавления единицы к младшему разряду. Для приведенного ранее примера имеем:
х_доп = х_пр = 0.1101 и у_доп = 1.0111.
В дополнительном коде нуль имеет единственное представление (+0)

---