Файл: Протокол 1 от 28 августа 2020 г. Конспект лекций содержание введение Краткая характеристика дисциплины.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 389
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
уст определяется суммой времени задержки переключения всех триггеров. Время установления Туст определяет быстродействие счетчика. Счетчики с последовательным переносом обладают сравнительно плохим быстродействием.
* Суммирующий двоичный счетчик с параллельным переносом
Наличие сигнала переноса в старший разряд определяется выражениями:
P12 = Q1C1; P23 = Q1Q2C; P34 = Q1Q2Q3C,
Где Р12 – сигнал переноса из первого разряда во второй;
Р23 – сигнал переноса из второго разряда в третий и т.п.
Для любого разряда Pn(n+1) = Q1Q2Q3, …, QnC
В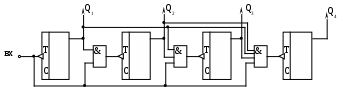
схеме счетчика с параллельным переносом сигналы переноса в каждый разряд формируются согласно приведенным формулам.
Рисунок 58 - Схема счетчика с параллельным переносом
Время установления кода при параллельной организации переноса определяется задержкой переключения одного триггера и временем задержки срабатывания схем И - существенно меньше, чем при последовательном переносе.
Недостаток - при большом числе разрядов требуются схемы И с большим числом входов.
* Суммирующий счетчик со сквозным переносом
При сквозном переносе триггеры счётчика объединяются в группы, внутри каждой группы осуществляется параллельный перенос, а между группами – последовательный. На рисунке 7 представлена схема счетчика со сквозным переносом, каждая группа которого содержит по два триггера.
При такой организации переноса все схемы умножения должны быть двухвходовыми.
Время установления кода в счетчике со сквозным переносом определяется задержкой переключения триггера, задержка переключения схем И и инвертора в одной группе и количеством групп.
Таким образом, быстродействие такого счетчика является промежуточным между быстродействиями счетчиков с последовательным и параллельным переносом.
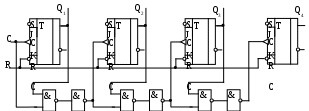
Рисунок 59 - Схема счетчика со сквозным переносом
2.4.5 Вычитающие счетчики
Счетчик обратного счета – при поступлении на вход очередного импульса вызывает уменьшение на единицу хранимого в счетчике числа. Т.о, выполняется вычитание единицы от предыдущего значения числа по правилам операции двоичного вычитания.
В вычитающем двоичном счетчике последовательные двоичные числа перебираются в обратном порядке, и при повторении последовательности максимальное число следует за нулем. На рисунке 8 приведена схема асинхронного трехразрядного двоичного вычитающего счетчика, построенного на базе D-триггеров.
Условия для изменения состояний триггеров вычитающих счетчиков аналогичны условиям для суммирующих счетчиков с той лишь разницей, что они должны “опираться” на значения инверсных, а не прямых выходов триггеров. Следовательно, рассмотренный выше счетчик можно превратить в вычитающий, просто переключив входы “С” триггеров с выходов Q на выходы . Когда в качестве разрядных триггеров используются D-триггеры, синхронизируемые передним фронтом синхроимпульсов, для получения вычитающего счетчика (асинхронного) входы “С” последующих триггеров соединяются с прямыми выходами предыдущих, как и в счетчике прямого счета на JK-триггерах.
Работа вычитающего счетчика на D-триггерах приведена на рисунке 8 б. После нулевого состояния всех триггеров, с приходом первого синхроимпульса они устанавливаются в состояние “1”. Поступление второго синхроимпульса приводит к уменьшению этого числа на одну единицу и т.д. После поступления восьмого импульса, все триггеры обнуляются и цикл счета повторяется, что соответствует Ксч = 8.
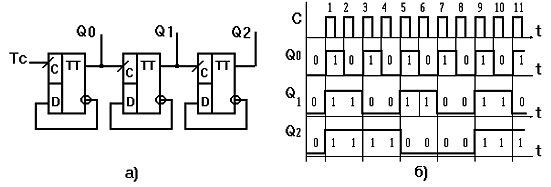
а) схема счетчика
б) временные диаграммы, поясняющие работу счетчика
Рисунок 60 - Асинхронный двоичный вычитающий счетчик на D-триггерах
Не двоичные счетчики - это счетчики с произвольным коэффициентом счета
, имеющие значение Ксч 2n.
Принцип построения подобного класса счетных устройств состоит в исключении нескольких состояний обычного двоичного счетчика, являющихся избыточными для счетчиков с коэффициентом пересчета, отличающимися от двоичных. При этом избыточные состояния исключаются с помощью обратных связей внутри счетчика.
Число избыточных состояний для любого счетчика определяется из следующего выражения:
М = 2n - Ксч,
где М - число запрещенных состояний,
Ксч - требуемый коэффициент счета;
2n - число устойчивых состояний двоичного счетчика.
Задача синтеза счетчика с произвольным коэффициентом счета заключается в определении необходимых обратных связей и минимизации их числа.
Для синтеза счетчика могут использоваться любые типы триггеров.
Требуемое количество триггеров определяется из выражения:
n= [log2 Ксч],
где [log2 Ксч] - двоичный логарифм заданного коэффициента пересчета Ксч, округленный до ближайшего целого числа.
ЗАДАЧА: Выполнить синтез схемы недвоичного счетчика с периодом цикла Ксч = 5, работающего в режиме сложения. Использовать для построения схемы синхронные JK – триггеры.
Выполним расчет неизвестных:
Ксч = 5
N = 2n – 1 = Ксч – 1, N = 5 – 1 = 4 – емкость счетчика
n= [log2 Ксч], n= [log2 5]
n= 3 – разрядность счетчика.
Составим таблицу работы счетчика согласно полученным данным.
Приведем таблицу переключения триггеров счетчика согласно таблице 17 и таблице 18.
Таблица 18 – Таблица переходов J K триггера
Таблица 19 – Таблица переключения триггеров счетчика
Приведем диаграммы Вейча –Карно
ШАБЛОН
J3 K3
J2 K2
J1 K1
Рисунок 61 - Диаграммы Вейча –Карно
В результате минимизации получены следующие выражения:
J3 = Q2Q1
K3 = 1
J2 = Q1
K2 = Q1
J 1 = Q3
1 = Q3
K1 = 1
Построим
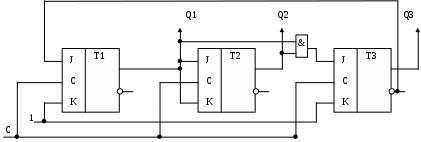
Рисунок 62 - Логическая схема счетчика
2.4.7 Особенности построения недвоичных счетчиков
В каждом отдельном случае приходится применять какие-то конкретные методы получения требуемого коэффициента счета. Существует несколько методов получения счетчиков с заданным коэффициентом пересчета Ксч. Один их этих методов заключается в немедленном сбросе в “0” счетчика, установившегося в комбинацию, соответствующему числу Ксч. Его называют также методом автосброса.
Рассмотрим пример реализации счетчика с Ксч=10 методом автосброса.
Очевидно, что “сбрасывая” двоичный четырехразрядный счетчик на нуль каждый раз, когда он будет принимать состояние 1010, можно обеспечить”возврат” счетчика в исходное состояние после каждых десяти импульсов. Подобный прием удобно применять при использовании счетчиков в интегральном исполнении, имеющих ячейки конъюнкции (И) на входах установки в нуль, как это сделано в микросхеме К1533ИЕ5. В данном примере организованы соединения, обеспечивающие коэффициент пересчета Ксч =10.
Таблица 20 – Таблица работы счетчика
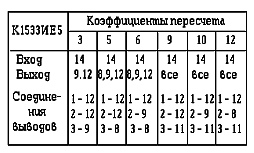
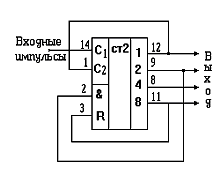
Рисунок 63 - Пример реализации счетчика с Ксч = 10
Как следует из рисунка 63, роль ячейки, выявляющей факт достижения кодовой комбинации 1010 на выходах счетчика, играет ячейка И, уже имеющаяся на входе сброса ИМС К1533ИЕ5.
В таблице 2 поясняются конфигурации соединений для получения различных коэффициентов пересчета с помощью счетчика К1533ИЕ5. Наиболее очевидные варианты получения коэффициентов (2, 4, 8, 16 ) в таблице не указаны.
В графе “Соединения” таблицы указано, какие выводы микросхемы должны быть соединены между собой: например, указание 1-12 означает, что нужно соединить вывод 1 с выводом 12. В строках “Ввод” и “Выход” таблицы указаны номера выводов микросхемы, на которые следует подавать входные импульсы и с которых надлежит снимать выходные, соответственно.
Следует отметить, что ИМС К1533ИЕ5 состоит из четырех счетных триггеров, один из которых имеет раздельные выводы входа и выхода, а остальные три триггера соединены последовательно по схеме асинхронного счетчика.
2.4.8 Реверсивный счётчик
В некоторых случаях необходимо, чтобы счетчик мог работать как в прямом, так и в обратном направлении счета. Такие счетчики называются реверсивными.
Реверсивные счетчики могут быть как асинхронного, так и синхронного типа. Они строятся путем применения логических коммутаторов (мультиплексоров) в цепях связи между триггерами.
Так, например, асинхронный реверсивный двоичный счетчик можно построить, если обеспечить подачу сигналов с прямого (при суммировании) или с инверсного (при вычитании) выхода предыдущего JK- или Т-триггера на счетный вход последующего.
В случае, когда реверсивный счетчик строится на базе D-триггеров, управляемых передним фронтом, для получения режима прямого счета следует соединить инверсный выход предыдущего с счетным входом последующего триггера.
Все рассмотренные типы счетчиков могут быть использованы в цифровых устройствах “умеренного” быстродействия, когда частота следования синхроимпульсов не превышает критического значения, при котором время задержки установки триггеров последних (старших) разрядов счетчика становится соизмеримым с длительностью периода входных тактовых импульсов. В связи с этим, асинхронные счетчики строятся на относительно небольшое количество разрядов, так как при большем количестве разрядов выходные сигналы триггеров старших разрядов появляются позднее, чем управляющие фронты синхроимпульсов (поступающих на вход первого триггера) .
Для построения вычитающего счетчика достаточно подать сигнал переноса на триггер старшего разряда не с прямого выхода предыдущего триггера, а с инверсного.
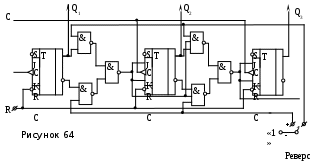
Связи между триггерами реверсивного счётчика соответствуют как суммирующему, так и вычитающему счётчику, но работает только одна из связей, которая определяется командой «Реверс» и подается на элемент И–НЕ, включенные в цепи передачи сигнала переноса. Схема реверсивного счётчика показана на рисунке 64.
2.4.9 Делители частоты. Назначение. Особенности построения
Цифровые последовательностные устройства, выполненные по схеме счетчика, но имеющие один счетный вход и один выход называются делителями частоты.
Любой счетчик может служить в качестве делителя частоты, если используется информация только одного из его выходов. Счетчики и делители имеют единую структуру, синтез делителя частоты соответствует синтезу счетчика.
Коэффициент счета счетчика численно совпадает с модулем деления делителя частоты. Счетчик по модулю 8 (Ксч = 8) позволяет реализовать делитель частоты на 8 без дополнительных схемных затрат. Это значит, что данный делитель делит частоту входной импульсной последовательности на 8.
* Суммирующий двоичный счетчик с параллельным переносом
Наличие сигнала переноса в старший разряд определяется выражениями:
P12 = Q1C1; P23 = Q1Q2C; P34 = Q1Q2Q3C,
Где Р12 – сигнал переноса из первого разряда во второй;
Р23 – сигнал переноса из второго разряда в третий и т.п.
Для любого разряда Pn(n+1) = Q1Q2Q3, …, QnC
В

схеме счетчика с параллельным переносом сигналы переноса в каждый разряд формируются согласно приведенным формулам.
Рисунок 58 - Схема счетчика с параллельным переносом
Время установления кода при параллельной организации переноса определяется задержкой переключения одного триггера и временем задержки срабатывания схем И - существенно меньше, чем при последовательном переносе.
Недостаток - при большом числе разрядов требуются схемы И с большим числом входов.
* Суммирующий счетчик со сквозным переносом
При сквозном переносе триггеры счётчика объединяются в группы, внутри каждой группы осуществляется параллельный перенос, а между группами – последовательный. На рисунке 7 представлена схема счетчика со сквозным переносом, каждая группа которого содержит по два триггера.
При такой организации переноса все схемы умножения должны быть двухвходовыми.
Время установления кода в счетчике со сквозным переносом определяется задержкой переключения триггера, задержка переключения схем И и инвертора в одной группе и количеством групп.
Таким образом, быстродействие такого счетчика является промежуточным между быстродействиями счетчиков с последовательным и параллельным переносом.

Рисунок 59 - Схема счетчика со сквозным переносом
2.4.5 Вычитающие счетчики
Счетчик обратного счета – при поступлении на вход очередного импульса вызывает уменьшение на единицу хранимого в счетчике числа. Т.о, выполняется вычитание единицы от предыдущего значения числа по правилам операции двоичного вычитания.
В вычитающем двоичном счетчике последовательные двоичные числа перебираются в обратном порядке, и при повторении последовательности максимальное число следует за нулем. На рисунке 8 приведена схема асинхронного трехразрядного двоичного вычитающего счетчика, построенного на базе D-триггеров.
Условия для изменения состояний триггеров вычитающих счетчиков аналогичны условиям для суммирующих счетчиков с той лишь разницей, что они должны “опираться” на значения инверсных, а не прямых выходов триггеров. Следовательно, рассмотренный выше счетчик можно превратить в вычитающий, просто переключив входы “С” триггеров с выходов Q на выходы . Когда в качестве разрядных триггеров используются D-триггеры, синхронизируемые передним фронтом синхроимпульсов, для получения вычитающего счетчика (асинхронного) входы “С” последующих триггеров соединяются с прямыми выходами предыдущих, как и в счетчике прямого счета на JK-триггерах.
Работа вычитающего счетчика на D-триггерах приведена на рисунке 8 б. После нулевого состояния всех триггеров, с приходом первого синхроимпульса они устанавливаются в состояние “1”. Поступление второго синхроимпульса приводит к уменьшению этого числа на одну единицу и т.д. После поступления восьмого импульса, все триггеры обнуляются и цикл счета повторяется, что соответствует Ксч = 8.

а) схема счетчика
б) временные диаграммы, поясняющие работу счетчика
Рисунок 60 - Асинхронный двоичный вычитающий счетчик на D-триггерах
Таблица 16 – Таблица переходов вычитающего счётчика для кода 8421
| № входного импульса | СОСТОЯНИЕ ТРИГГЕРОВ СЧЕТЧИКА | |||||||
| ТЕКУЩЕЕ | СЛЕДУЮЩЕЕ | |||||||
| Q4 | Q3 | Q2 | Q1 | Q4’ | Q3’ | Q2’ | Q1’ | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 4 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 8 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 10 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
-
Недвоичные счетчики
Не двоичные счетчики - это счетчики с произвольным коэффициентом счета
, имеющие значение Ксч 2n.
Принцип построения подобного класса счетных устройств состоит в исключении нескольких состояний обычного двоичного счетчика, являющихся избыточными для счетчиков с коэффициентом пересчета, отличающимися от двоичных. При этом избыточные состояния исключаются с помощью обратных связей внутри счетчика.
Число избыточных состояний для любого счетчика определяется из следующего выражения:
М = 2n - Ксч,
где М - число запрещенных состояний,
Ксч - требуемый коэффициент счета;
2n - число устойчивых состояний двоичного счетчика.
Задача синтеза счетчика с произвольным коэффициентом счета заключается в определении необходимых обратных связей и минимизации их числа.
Для синтеза счетчика могут использоваться любые типы триггеров.
Требуемое количество триггеров определяется из выражения:
n= [log2 Ксч],
где [log2 Ксч] - двоичный логарифм заданного коэффициента пересчета Ксч, округленный до ближайшего целого числа.
ЗАДАЧА: Выполнить синтез схемы недвоичного счетчика с периодом цикла Ксч = 5, работающего в режиме сложения. Использовать для построения схемы синхронные JK – триггеры.
Выполним расчет неизвестных:
Ксч = 5
N = 2n – 1 = Ксч – 1, N = 5 – 1 = 4 – емкость счетчика
n= [log2 Ксч], n= [log2 5]
n= 3 – разрядность счетчика.
Составим таблицу работы счетчика согласно полученным данным.
Таблица 17 – Таблица переходов суммирующего счётчика
| № входного импульса | СОСТОЯНИЕ ТРИГГЕРОВ СЧЕТЧИКА | |||||
| ТЕКУЩЕЕ | СЛЕДУЮЩЕЕ | |||||
| Q3 | Q2 | Q1 | Q3’ | Q2’ | Q1’ | |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 | 1 | 0 |
| 3 | 0 | 1 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 1 | 1 | 0 | 0 |
| 5 | 1 | 0 | 0 | 0 | 0 | 0 |
Приведем таблицу переключения триггеров счетчика согласно таблице 17 и таблице 18.
Таблица 18 – Таблица переходов J K триггера
| Вид перехода | J | K |
| 0→0 | 0 | - |
| 0→1 | 1 | - |
| 1→0 | - | 1 |
| 1→1 | - | 0 |
Таблица 19 – Таблица переключения триггеров счетчика
| № имп. на входе счётчика | Состояние триггеров первой декады | ||||||||
| Т3 | Т2 | Т1 | |||||||
| Q3 – Q3’ | J3 | K3 | Q2 – Q2’ | J2 | K2 | Q1 – Q1’ | J1 | K1 | |
| 1 | 0→0 | 0 | - | 0→0 | 0 | - | 0→1 | 1 | - |
| 2 | 0→0 | 0 | - | 0→1 | 1 | - | 1→0 | - | 1 |
| 3 | 0→0 | 0 | - | 1→1 | - | 0 | 0→1 | 1 | - |
| 4 | 0→1 | 1 | - | 1→0 | - | 1 | 1→0 | - | 1 |
| 5 | 1→0 | - | 1 | 0→0 | 0 | - | 0→0 | 0 | - |
Приведем диаграммы Вейча –Карно
ШАБЛОН
| Q2Q1 Q4Q3 | 00 | 01 | 11 | 10 |
| 0 | 1 | 2 | 4 | 3 |
| 1 | 5 | - | - | - |
J3 K3
| Q2Q1 Q3 | 00 | 01 | 11 | 10 |
| 0  | 0 | 0 | 1 | 0 |
| 1 | - | - | - | - |
| Q2Q1 Q3 | 00 | 01 | 11 | 10 |
| 0 | - | - | - | - |
| 1 | 1 | - | - | - |
J2 K2
| Q2Q1 Q3 | 00 | 01 | 11 | 10 |
| 0 | - | - | 1 | 0 |
| 1 | - | - | - | - |
| Q2Q1 Q3 | 00 | 01 | 11 | 10 |
| 0 | 0 | 1 | - | - |
| 1 | 0 | - | - | - |
J1 K1
| Q2Q1 Q3 | 00 | 01 | 11 | 10 |
| 0 | 1 | - | - | 1 |
| 1 | 0 | - | - | - |
| Q2Q1 Q3 | 00 | 01 | 11 | 10 |
| 0 | - | 1 | 1 | - |
| 1 | - | - | - | - |
Рисунок 61 - Диаграммы Вейча –Карно
В результате минимизации получены следующие выражения:
J3 = Q2Q1
K3 = 1
J2 = Q1
K2 = Q1
J
 1 = Q3
1 = Q3K1 = 1
Построим

Рисунок 62 - Логическая схема счетчика
2.4.7 Особенности построения недвоичных счетчиков
В каждом отдельном случае приходится применять какие-то конкретные методы получения требуемого коэффициента счета. Существует несколько методов получения счетчиков с заданным коэффициентом пересчета Ксч. Один их этих методов заключается в немедленном сбросе в “0” счетчика, установившегося в комбинацию, соответствующему числу Ксч. Его называют также методом автосброса.
Рассмотрим пример реализации счетчика с Ксч=10 методом автосброса.
Очевидно, что “сбрасывая” двоичный четырехразрядный счетчик на нуль каждый раз, когда он будет принимать состояние 1010, можно обеспечить”возврат” счетчика в исходное состояние после каждых десяти импульсов. Подобный прием удобно применять при использовании счетчиков в интегральном исполнении, имеющих ячейки конъюнкции (И) на входах установки в нуль, как это сделано в микросхеме К1533ИЕ5. В данном примере организованы соединения, обеспечивающие коэффициент пересчета Ксч =10.
Таблица 20 – Таблица работы счетчика


Рисунок 63 - Пример реализации счетчика с Ксч = 10
Как следует из рисунка 63, роль ячейки, выявляющей факт достижения кодовой комбинации 1010 на выходах счетчика, играет ячейка И, уже имеющаяся на входе сброса ИМС К1533ИЕ5.
В таблице 2 поясняются конфигурации соединений для получения различных коэффициентов пересчета с помощью счетчика К1533ИЕ5. Наиболее очевидные варианты получения коэффициентов (2, 4, 8, 16 ) в таблице не указаны.
В графе “Соединения” таблицы указано, какие выводы микросхемы должны быть соединены между собой: например, указание 1-12 означает, что нужно соединить вывод 1 с выводом 12. В строках “Ввод” и “Выход” таблицы указаны номера выводов микросхемы, на которые следует подавать входные импульсы и с которых надлежит снимать выходные, соответственно.
Следует отметить, что ИМС К1533ИЕ5 состоит из четырех счетных триггеров, один из которых имеет раздельные выводы входа и выхода, а остальные три триггера соединены последовательно по схеме асинхронного счетчика.
2.4.8 Реверсивный счётчик
В некоторых случаях необходимо, чтобы счетчик мог работать как в прямом, так и в обратном направлении счета. Такие счетчики называются реверсивными.
Реверсивные счетчики могут быть как асинхронного, так и синхронного типа. Они строятся путем применения логических коммутаторов (мультиплексоров) в цепях связи между триггерами.
Так, например, асинхронный реверсивный двоичный счетчик можно построить, если обеспечить подачу сигналов с прямого (при суммировании) или с инверсного (при вычитании) выхода предыдущего JK- или Т-триггера на счетный вход последующего.
В случае, когда реверсивный счетчик строится на базе D-триггеров, управляемых передним фронтом, для получения режима прямого счета следует соединить инверсный выход предыдущего с счетным входом последующего триггера.
Все рассмотренные типы счетчиков могут быть использованы в цифровых устройствах “умеренного” быстродействия, когда частота следования синхроимпульсов не превышает критического значения, при котором время задержки установки триггеров последних (старших) разрядов счетчика становится соизмеримым с длительностью периода входных тактовых импульсов. В связи с этим, асинхронные счетчики строятся на относительно небольшое количество разрядов, так как при большем количестве разрядов выходные сигналы триггеров старших разрядов появляются позднее, чем управляющие фронты синхроимпульсов (поступающих на вход первого триггера) .
Для построения вычитающего счетчика достаточно подать сигнал переноса на триггер старшего разряда не с прямого выхода предыдущего триггера, а с инверсного.

Связи между триггерами реверсивного счётчика соответствуют как суммирующему, так и вычитающему счётчику, но работает только одна из связей, которая определяется командой «Реверс» и подается на элемент И–НЕ, включенные в цепи передачи сигнала переноса. Схема реверсивного счётчика показана на рисунке 64.
2.4.9 Делители частоты. Назначение. Особенности построения
Цифровые последовательностные устройства, выполненные по схеме счетчика, но имеющие один счетный вход и один выход называются делителями частоты.
Любой счетчик может служить в качестве делителя частоты, если используется информация только одного из его выходов. Счетчики и делители имеют единую структуру, синтез делителя частоты соответствует синтезу счетчика.
Коэффициент счета счетчика численно совпадает с модулем деления делителя частоты. Счетчик по модулю 8 (Ксч = 8) позволяет реализовать делитель частоты на 8 без дополнительных схемных затрат. Это значит, что данный делитель делит частоту входной импульсной последовательности на 8.