Файл: Протокол 1 от 28 августа 2020 г. Конспект лекций содержание введение Краткая характеристика дисциплины.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 405
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
значениям функции равным «1» (у=1). Каждая комбинация входных сигналов (аргументов Х) на этих значениях функции записывается в виде логического произведения (конъюнкции). Причем, если входной сигнал в этой комбинации равен «0»(Х=0), то записывается его отрицание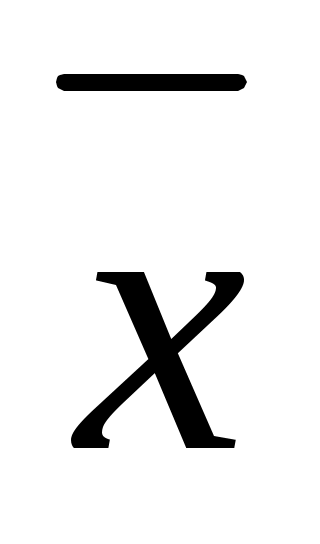 
, если же он равен «1»(Х=1), то записывается его прямое значение Х. Само выражение логической функции записывается в виде логического сложения (дизъюнкции) этих произведений (конъюнкций).
В таблице 1 функция равна «1» (y=1) на следующих наборах аргументов: №3, №5, №6, №7. Запишем логические произведения для каждого указанного набора:
Набор №3: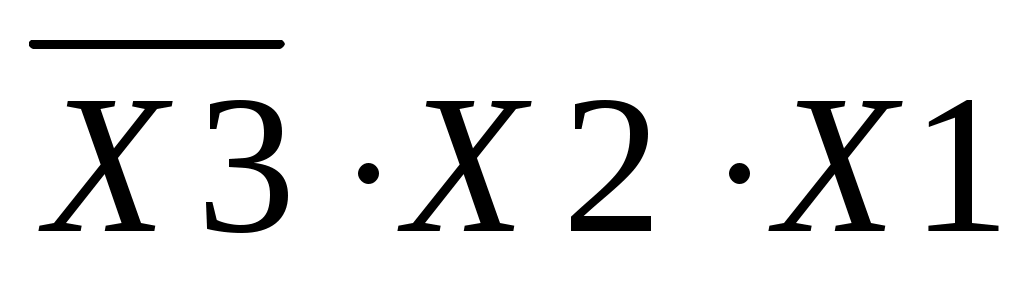
Набор №5: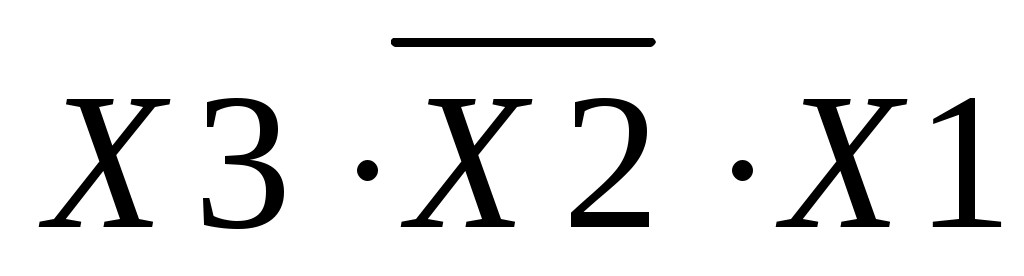
Набор №6: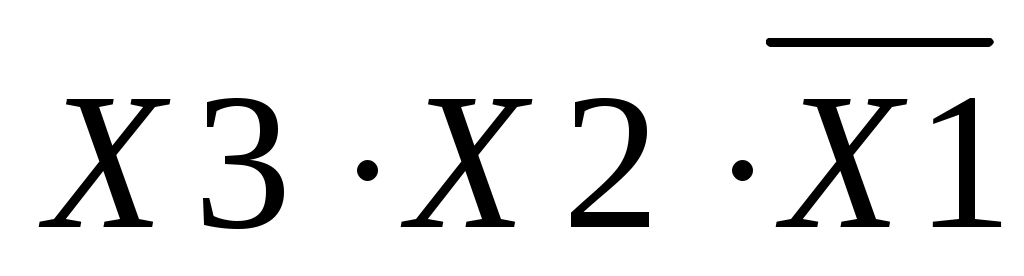
Набор №7: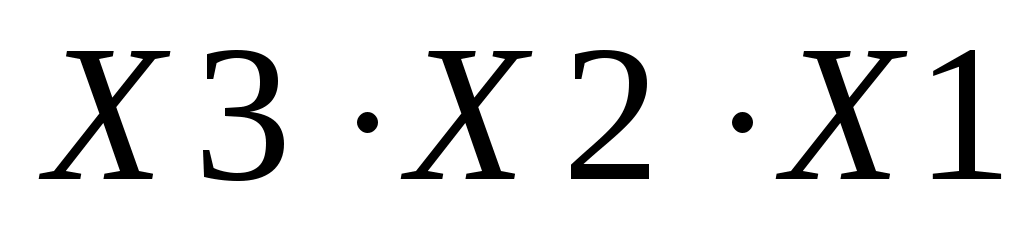
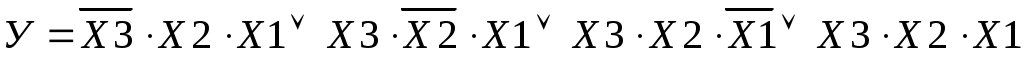
Для записи логической функции в форме СНКФ необходимо выбрать те комбинации (наборы) логических аргументов, где функция равна «0» (у=0). Каждый набор аргументов необходимо представить в виде логического сложения (дизъюнкции). Причем, если входной сигнал равен «1» (Х=1), то записывается его отрицание (инверсия)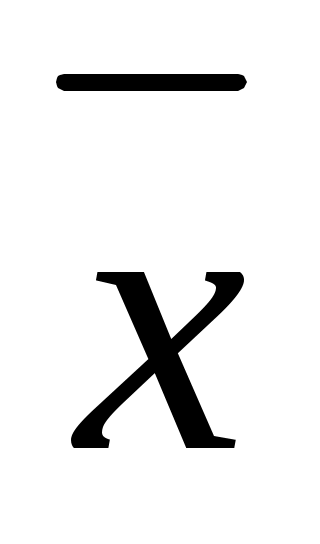 . Если же он равен «0», то записывается его значение Х. Конечное логическое выражение записывается в виде логических произведений (конъюнкций) наборов.
В таблице 1 функция у равна « 0» на следующих наборах аргументов: №0, №1, №2, №4. Запишем логические сложения для каждого указанного набора:
Набор №0: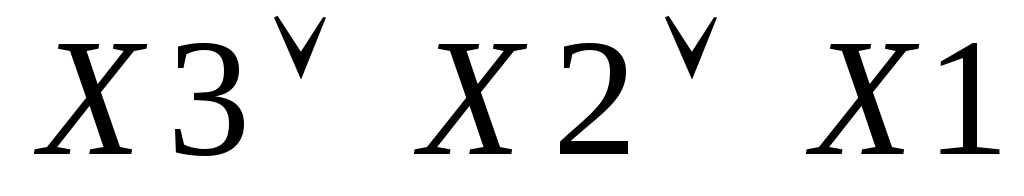
Набор №1: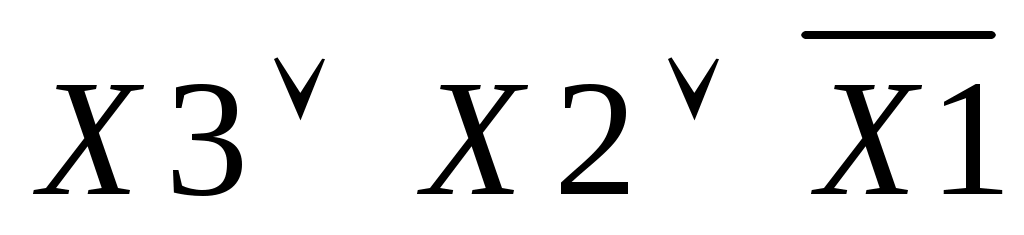
Набор №2: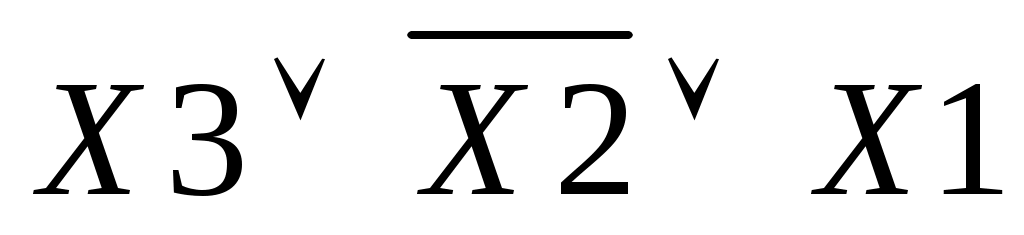
Набор №4: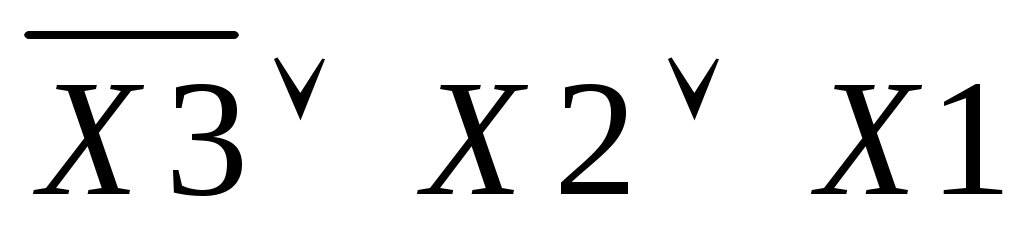
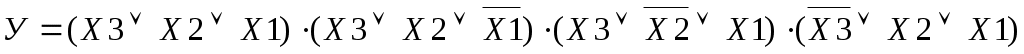
Запись функции в СНДФ или СНКФ зависит от того, как задана функция у: если задано больше значений у=1, то функцию целесообразно записать в СНКФ, если больше значений у=0, то --в СНДФ.
Логическая функция может быть задана в форме НДФ или НКФ и не являться совершенной.
Функция несовершенна, если в записи логического выражения (в простом сложении для КФ или простом умножении для ДФ) отсутствует один и более аргументов Х, образующих функцию.
Если в ДФ в элементарном произведении или в КФ в элементарной сумме один и тот же аргумент Х или его инверсия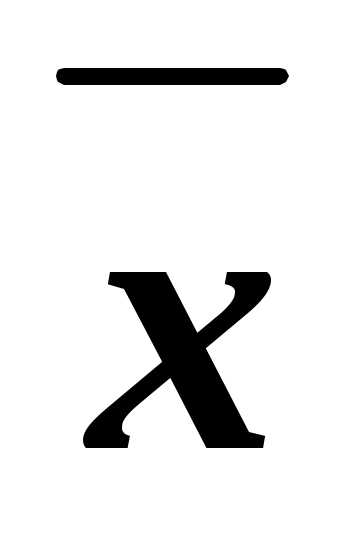
не повторяется, то функция является нормальной.
Пример 3:
а) НДФ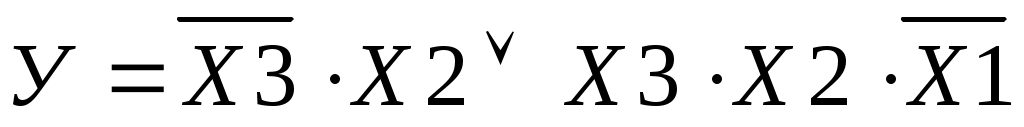
б) НКФ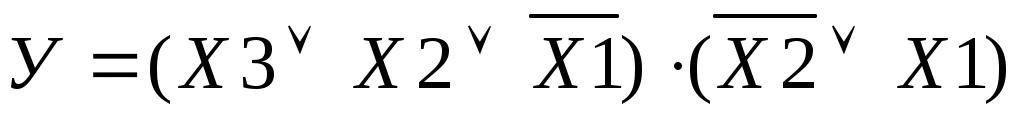
В примере 3 а) в первой простой конъюнкции отсутствует прямое значение аргумента Х1 или его инверсии;
В примере 3 б) во второй простой конъюнкции отсутствует значение аргумента Х3 или его инверсия.
В следующих двух выражениях функция не является нормальной и совершенной. Функция ДФ несовершенна, так как в первой простой конъюнкции отсутствует значение аргумента Х3 или его инверсия. Нормальный вид функции ДФ нарушает второе значение аргумента Х1 в первой простой конъюнкции и значение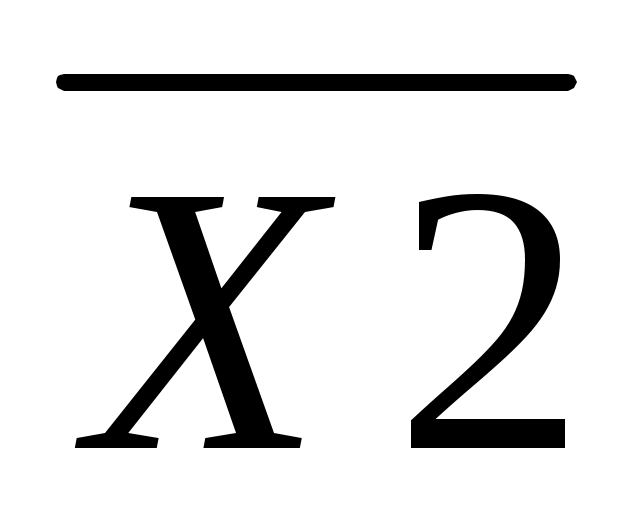
во второй.
Совершенный вид функции КФ нарушает отсутствие значений Х1, Х3 и их инверсии в первой простой дизъюнкции, а также отсутствие значений Х1, Х2 и их инверсии на месте третьей простой дизъюнкции. Функция не является нормальной, так как на месте первой простой дизъюнкции приведены два одинаковых значения аргументов Х2.
ДФ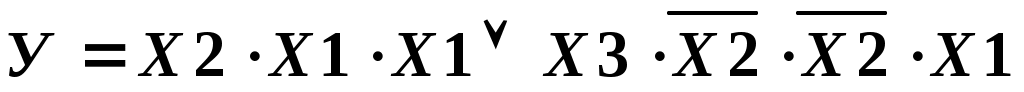
К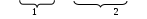
Ф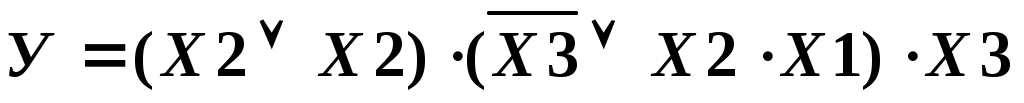
ЦИФРОВОЙ способ представления позволяет получить компактное логическое выражение, в котором присутствуют номера наборов аргументов. Для функции СНДФ под знаком суммы перечисляются номера наборов (в порядке возрастания), на которых функция принимает значение «1». Все оставшиеся наборы функции (таблица 1) будут записываться под знаком произведения.
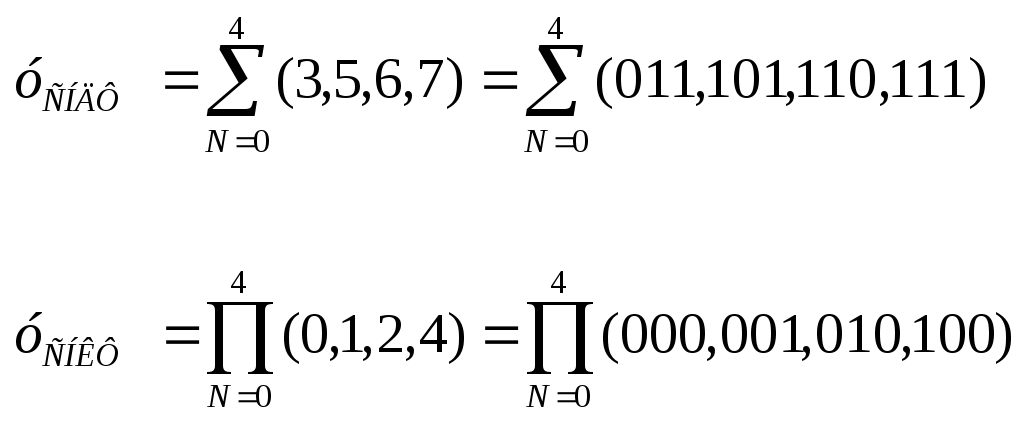
На основании такой записи можно легко перейти к алгебраической записи логической функции.
Ц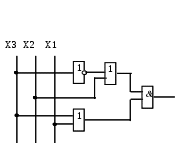
ИФРОВОЙ способ представления логических функций также подразумевает представление логической функции в виде схемы цифрового устройства.
Например,
Рисунок 7 –Логическая схема устройства на элементах И, ИЛИ, НЕ
1.2.3
Логические функции одного и двух аргументов
Общее количество всех возможных функций для “x” аргументов определяется количеством комбинаций из 2x разрядов и равно числу:
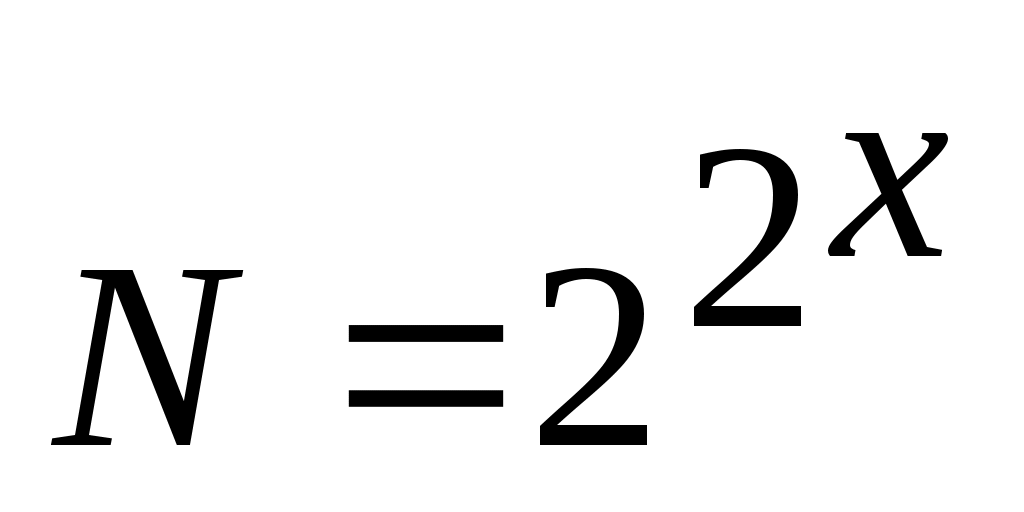
Для каждой логической функции можно составить таблицу истинности, в которой указывается число аргументов, образующих функцию, все возможные значения наборов аргументов “x” и значение функции на каждом из наборов.
Кроме того, логическую функцию можно записать в виде логического выражения и присвоить элементу, выполняющему данную ЛФ, свое УГО (условное графическое обозначение).
Примеры ЛФ, образованных от различного числа аргументов, рассмотрены ниже. Логические функции 1 аргумента называются элементарными, т.к. логические выражения этих функций содержат не более одной логической операции.
* Логические функции одного аргумента
Следует учесть, что аргумент «Х» может принимать два (n=2) значения, т.е. Х=0 и Х=1.
Согласно формуле (2) от одного аргумента «Х» можно образовать 4 различных логических функций (f0 –f3).
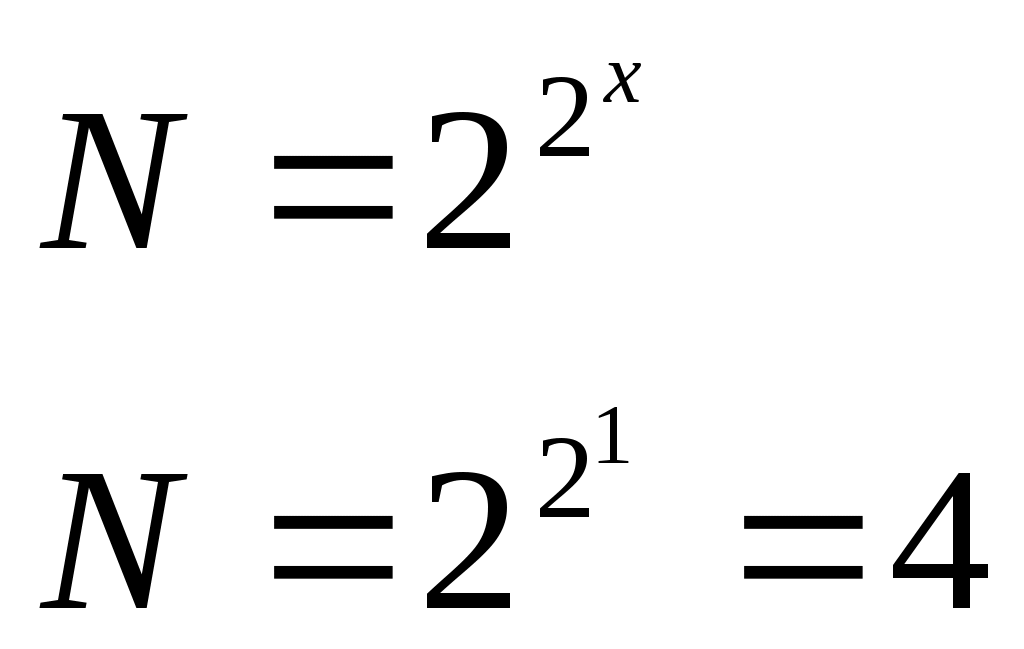
Каждой логической функции соответствует свой логический элемент.
Логические функции одного аргумента приведены в таблице 1. Таблицы истинности этих функций указаны в таблице 2.
Логическая функция f0 независимо от значения аргумента «Х», равна нулю (f0=0). Такую функцию называют «постоянный нуль» (const 0).
Логическая функция f1 на выходе логического элемента принимает значение, соответствующее значению аргумента «Х», подаваемого на его вход (f1=Х). Такую функцию называют «аргумент Х».
Функция f1 = x представляет собой логическую операцию “повтор”. Логический элемент, реализующий эту операцию, называется “повторитель”.
Логическая функция f2 принимает значение, обратное значению аргумента «Х», действующему на входе логического элемента(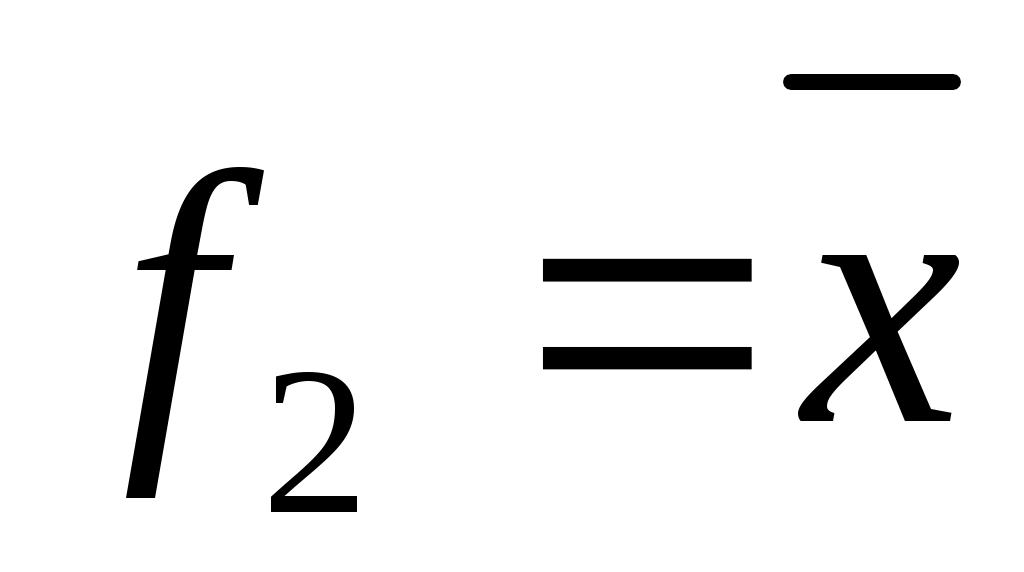
). Если Х=0, то f2=1,если Х=1, то f2=0. Такую функцию называют «инверсия Х».
Функция f2 =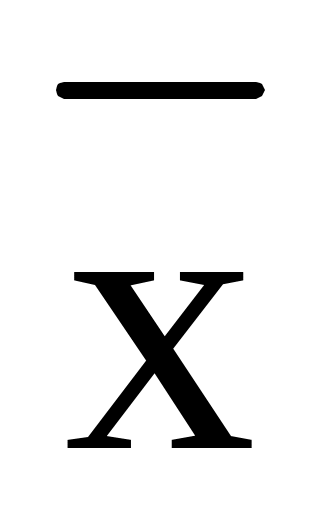
носит название “инверсии” или “отрицания ” и представляет собой логическую операцию (действие) НЕ. Логический элемент, реализующий операцию логического отрицания называется элементом НЕ (инвертором).
Логическая функция f3 независимо от значения аргумента «Х», принимает значение единицы (f3=1). Она называется «постоянная единица» (const 1).
Логические функции f0 и f3 не имеют своего логического элемента, так как являются источниками постоянного сигнала (генератором).
Логические элементы (их УГО), реализующие функции f1 и f2 приведены на рисунке 1.
а) повторитель б) инвертор
Рисунок 8 – УГО элементов
Таблица 7 – Логические функции одного аргумента
Таблица 8 – Таблица истинности логических функций
Указанные в таблице 2 логические функции обладают следующими свойствами.
, если же он равен «1»(Х=1), то записывается его прямое значение Х. Само выражение логической функции записывается в виде логического сложения (дизъюнкции) этих произведений (конъюнкций).В таблице 1 функция равна «1» (y=1) на следующих наборах аргументов: №3, №5, №6, №7. Запишем логические произведения для каждого указанного набора:
Набор №3:
Набор №5:
Набор №6:
Набор №7:
Для записи логической функции в форме СНКФ необходимо выбрать те комбинации (наборы) логических аргументов, где функция равна «0» (у=0). Каждый набор аргументов необходимо представить в виде логического сложения (дизъюнкции). Причем, если входной сигнал равен «1» (Х=1), то записывается его отрицание (инверсия)
. Если же он равен «0», то записывается его значение Х. Конечное логическое выражение записывается в виде логических произведений (конъюнкций) наборов.В таблице 1 функция у равна « 0» на следующих наборах аргументов: №0, №1, №2, №4. Запишем логические сложения для каждого указанного набора:
Набор №0:
Набор №1:
Набор №2:
Набор №4:
Запись функции в СНДФ или СНКФ зависит от того, как задана функция у: если задано больше значений у=1, то функцию целесообразно записать в СНКФ, если больше значений у=0, то --в СНДФ.
Логическая функция может быть задана в форме НДФ или НКФ и не являться совершенной.
Функция несовершенна, если в записи логического выражения (в простом сложении для КФ или простом умножении для ДФ) отсутствует один и более аргументов Х, образующих функцию.
Если в ДФ в элементарном произведении или в КФ в элементарной сумме один и тот же аргумент Х или его инверсия
не повторяется, то функция является нормальной.Пример 3:
а) НДФ
б) НКФ
В примере 3 а) в первой простой конъюнкции отсутствует прямое значение аргумента Х1 или его инверсии;
В примере 3 б) во второй простой конъюнкции отсутствует значение аргумента Х3 или его инверсия.
В следующих двух выражениях функция не является нормальной и совершенной. Функция ДФ несовершенна, так как в первой простой конъюнкции отсутствует значение аргумента Х3 или его инверсия. Нормальный вид функции ДФ нарушает второе значение аргумента Х1 в первой простой конъюнкции и значение
во второй. Совершенный вид функции КФ нарушает отсутствие значений Х1, Х3 и их инверсии в первой простой дизъюнкции, а также отсутствие значений Х1, Х2 и их инверсии на месте третьей простой дизъюнкции. Функция не является нормальной, так как на месте первой простой дизъюнкции приведены два одинаковых значения аргументов Х2.
ДФ
К
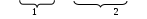
Ф
ЦИФРОВОЙ способ представления позволяет получить компактное логическое выражение, в котором присутствуют номера наборов аргументов. Для функции СНДФ под знаком суммы перечисляются номера наборов (в порядке возрастания), на которых функция принимает значение «1». Все оставшиеся наборы функции (таблица 1) будут записываться под знаком произведения.
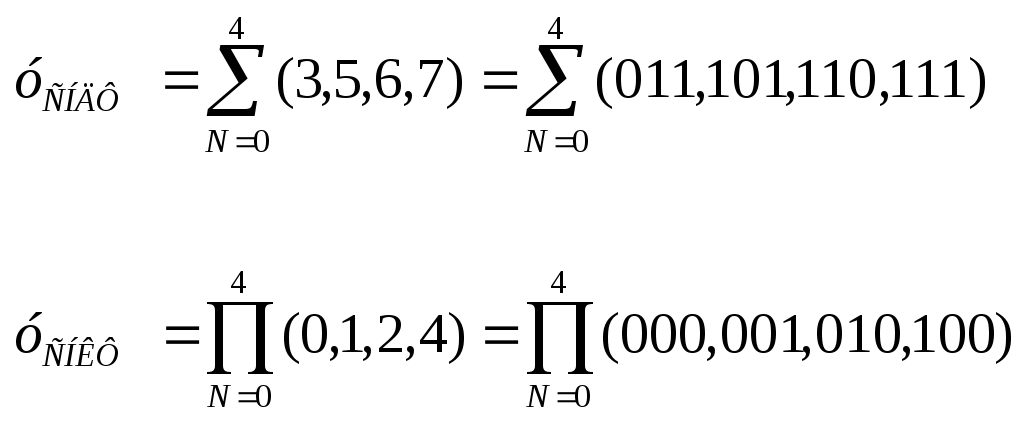
На основании такой записи можно легко перейти к алгебраической записи логической функции.
Ц
ИФРОВОЙ способ представления логических функций также подразумевает представление логической функции в виде схемы цифрового устройства.Например,
Рисунок 7 –Логическая схема устройства на элементах И, ИЛИ, НЕ
1.2.3
Логические функции одного и двух аргументов
Общее количество всех возможных функций для “x” аргументов определяется количеством комбинаций из 2x разрядов и равно числу:
Для каждой логической функции можно составить таблицу истинности, в которой указывается число аргументов, образующих функцию, все возможные значения наборов аргументов “x” и значение функции на каждом из наборов.
Кроме того, логическую функцию можно записать в виде логического выражения и присвоить элементу, выполняющему данную ЛФ, свое УГО (условное графическое обозначение).
Примеры ЛФ, образованных от различного числа аргументов, рассмотрены ниже. Логические функции 1 аргумента называются элементарными, т.к. логические выражения этих функций содержат не более одной логической операции.
* Логические функции одного аргумента
Следует учесть, что аргумент «Х» может принимать два (n=2) значения, т.е. Х=0 и Х=1.
Согласно формуле (2) от одного аргумента «Х» можно образовать 4 различных логических функций (f0 –f3).
Каждой логической функции соответствует свой логический элемент.
Логические функции одного аргумента приведены в таблице 1. Таблицы истинности этих функций указаны в таблице 2.
Логическая функция f0 независимо от значения аргумента «Х», равна нулю (f0=0). Такую функцию называют «постоянный нуль» (const 0).
Логическая функция f1 на выходе логического элемента принимает значение, соответствующее значению аргумента «Х», подаваемого на его вход (f1=Х). Такую функцию называют «аргумент Х».
Функция f1 = x представляет собой логическую операцию “повтор”. Логический элемент, реализующий эту операцию, называется “повторитель”.
Логическая функция f2 принимает значение, обратное значению аргумента «Х», действующему на входе логического элемента(
). Если Х=0, то f2=1,если Х=1, то f2=0. Такую функцию называют «инверсия Х».
Функция f2 =
носит название “инверсии” или “отрицания ” и представляет собой логическую операцию (действие) НЕ. Логический элемент, реализующий операцию логического отрицания называется элементом НЕ (инвертором).Логическая функция f3 независимо от значения аргумента «Х», принимает значение единицы (f3=1). Она называется «постоянная единица» (const 1).
Логические функции f0 и f3 не имеют своего логического элемента, так как являются источниками постоянного сигнала (генератором).
Логические элементы (их УГО), реализующие функции f1 и f2 приведены на рисунке 1.
а) повторитель б) инвертор
Рисунок 8 – УГО элементов
Таблица 7 – Логические функции одного аргумента
| Обозначение функции | f0 = 0 | f1 = x | f2 =  | f3 = 1 |
| Название функции | Постоян. “0” генератор | аргумент “x” | Инверсия ”х” | Постоян. “1” генератор |
| Логические элементы | - | повторитель | Инвертор | - |
Таблица 8 – Таблица истинности логических функций
| Аргумент “x” | Функции | |||
| f0 | f1 | f2 | f3 | |
| 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
Указанные в таблице 2 логические функции обладают следующими свойствами.