Файл: Протокол 1 от 28 августа 2020 г. Конспект лекций содержание введение Краткая характеристика дисциплины.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 409
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2 = 0.Во всех остальных случаях функция равна “1”.
Она задается таблицей истинности приведенной в таблице 13.
Таблица 13 Таблица 14
Логическая функция “импликация” от X2 к X1 (f11) обозначается как
f11 = X2 X1
ее значение определяется по формуле f11 =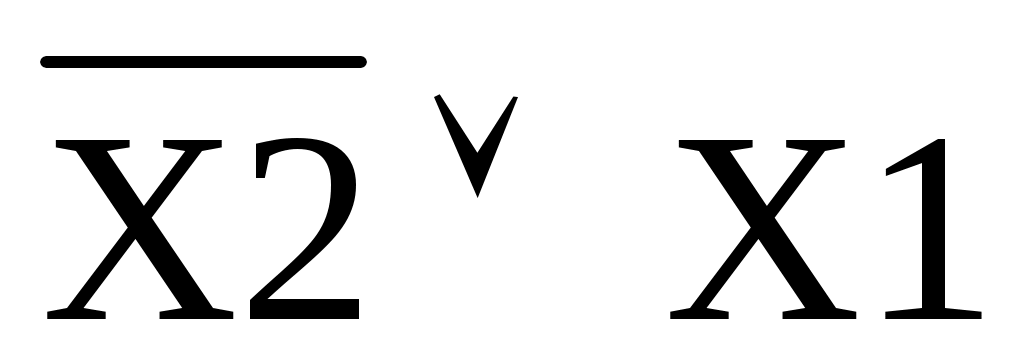
Функция будет равна “0” только в том случае, когда
X2 = 1; X1 = 0. Во всех остальных случаях функция “истинна” (равна “1”). Таблица приведена в таблице 14.
Логические функции f2 и f4 являются функциями, выполняющими операцию запрета (отрицание импликации).
Логическая функция f2 выполняет операцию запрета по X2 (отрицание импликации f13
). Она задается формулой
f2 = X1 X2=Х1∆Х2
и ее значение определяется как: f2 =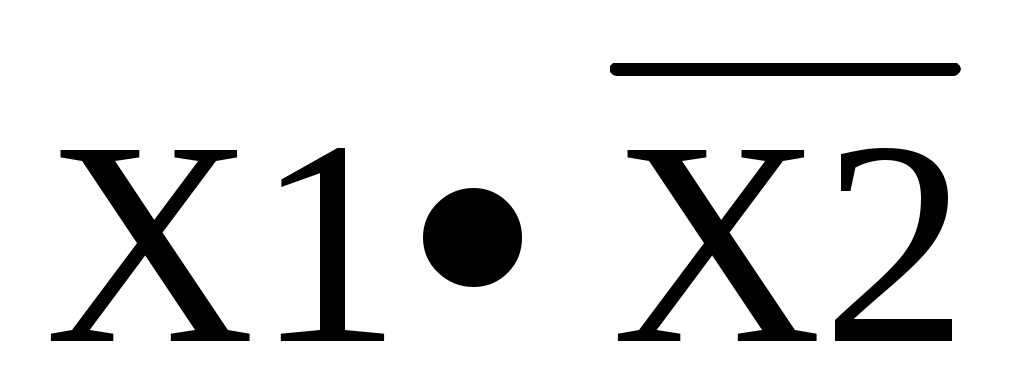
Таким образом, f2 =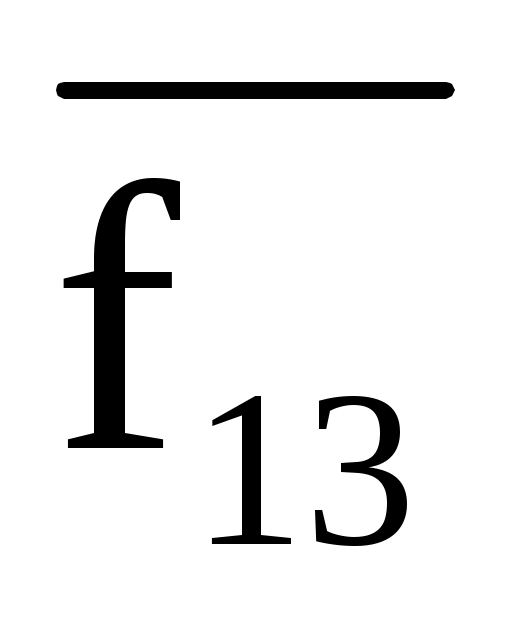
. По теореме Моргана доказываем утверждение
f13 =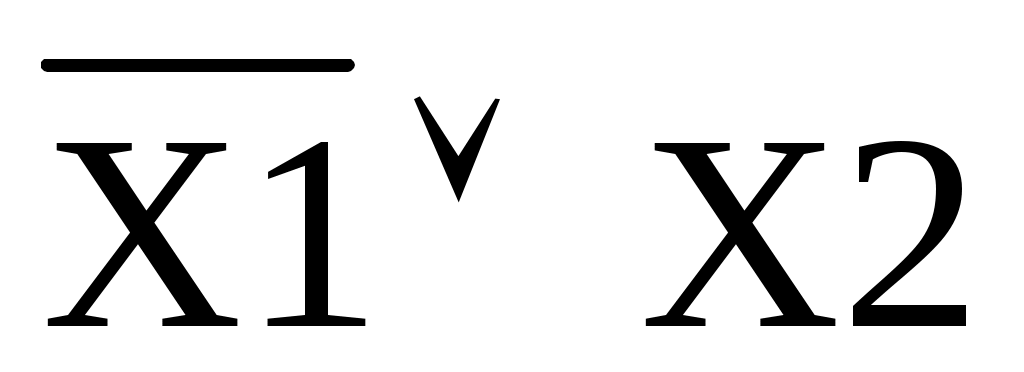
f2 =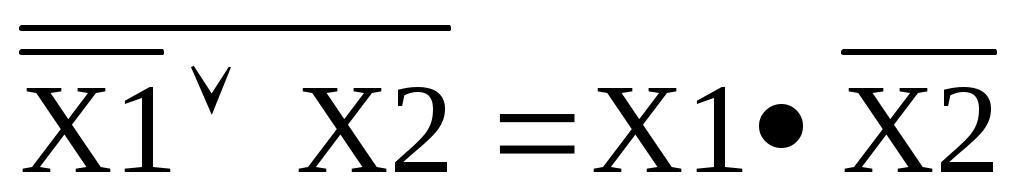
Логическая функция f4 выполняет операцию запрета по X1 (отрицание импликации f11)
f4 = X2 X1=Х2∆Х1
Значение функции в таблице истинности определяется как:
f4 =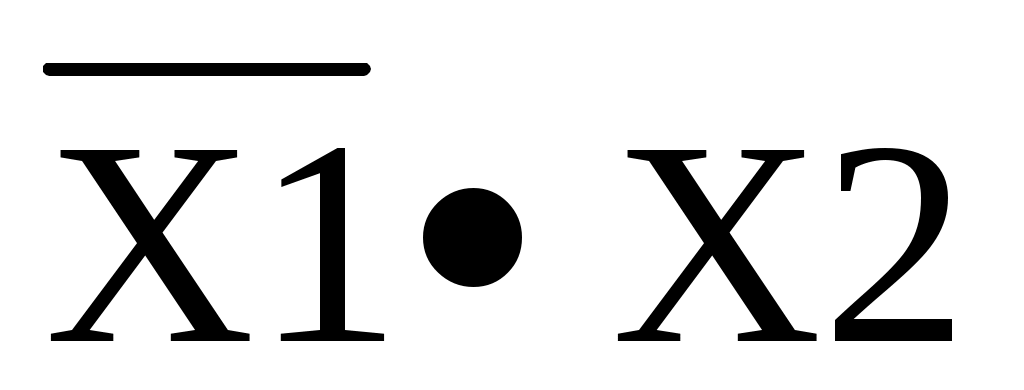
Согласно свойств логических функций f4 =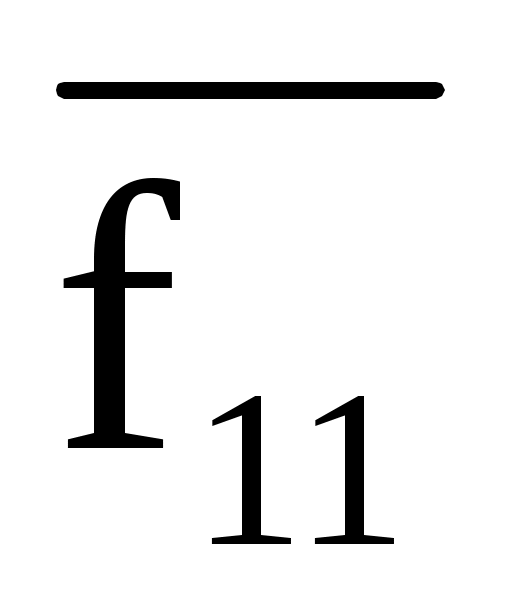
, т.е.
f11 =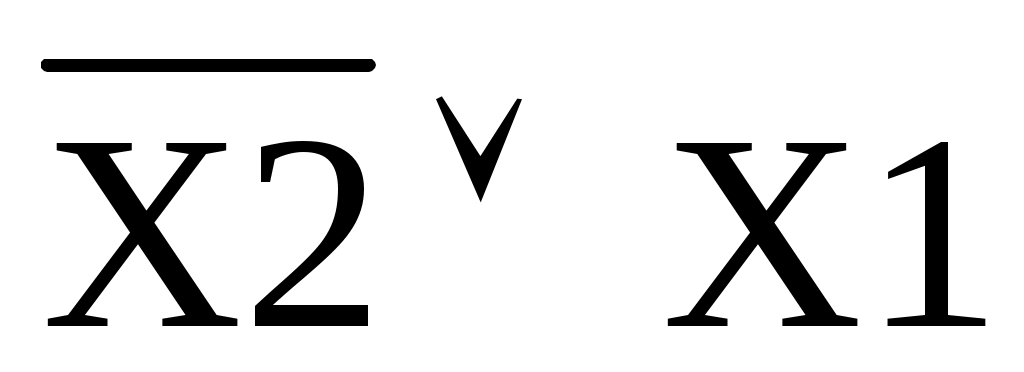
f4 =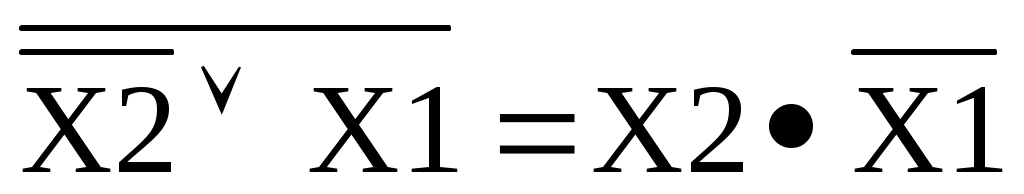
что соответствует исходному значению f4.
Таблицы истинности функций f2 (таблица 15) и f4 (таблица 16) приведены ниже.
Таблица 15 Таблица 16
Удобно все таблицы истинности функций 2-х аргументов представить в виде одной общей таблицы (таблица17). Возле нее указана связь логических функций в виде стрелок. Они указывают на попарную инверсию соответствующих функций.
Таблица 17 – Логические функции 1 и 2 аргументов
На рисунке 9 приведены УГО логических элементов для некоторых функций.
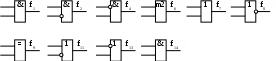
Рисунок 9
Рассмотренные логические функции являются элементарными, так как содержат не более одной логической операции. С помощью их можно описать любое логическое устройство и построить его схему.
* Логический элемент «И-НЕ» - элемент ЩЕФФЕРА
Логический элемент «И-НЕ» Выполняет действие логического отрицания умножения аргументов Х1, Х2, ... Хn (отрицание конъюнкции).
Логическая функция принимает значение ложь (Y=0) только в том случае, если все аргументы Х, участвующие в операции логического отрицания умножения, - истинны (Х1=Х2=...=Хn=1).
Если хотя бы один из аргументов Х равен нулю (X=0), то логическая функция Y равна единице (Y=1) - истинна.
Данная функция является сложной. Условно можно считать, что функция состоит из двух операций. Вначале выполняется логическая операция умножения, а затем инверсия.
Алгебраическая запись операции «И-НЕ», образованной от двух аргументов, имеет вид:
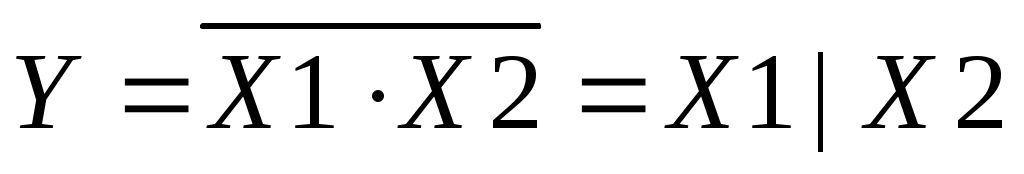
Читается: Функция У равна Х1 «штрих» Х2.
Знак « | » обозначают действие «И-НЕ».
Условно-графическое изображение элемента «И-НЕ» представлено на рисунке 10.
Р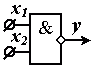
исунок 10 - Условно-графическое изображение элемента «И-НЕ»
Таблица истинности логического элемента «И-НЕ» имеет вид:
Таблица 18
Свойство операции «И-НЕ»: Функция равна «0» только в том случае, если все аргументы, образующие функцию равны «1» (Х1=Х2=1). Если хотя бы один из аргументов «Х», образующий функцию равен «0» (Х1=0 либо Х2=0), то функция обращается в единицу «У=1».
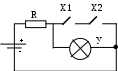
Рисунок 11 – Электрическая схема для элемента «ИЛИ»
Ключи разомкнуты – Х1=Х2=0, лампочка горит – У=1.
Один из ключей замкнут – Х1=1, Х2=0 (либо Х1=0, Х2=1), лампочка горит – У=1.
Оба ключа замкнуты - Х1=Х2=1, лампочка гаснет– У=0.
* Логический элемент «ИЛИ-НЕ» - элемент ПИРСА
Логический элемент «ИЛИ-НЕ» Выполняет действие логического отрицания сложения аргументов Х1, Х2, ... Хn (отрицание дизъюнкции).
Логическая функция истинна (Y=1) только в том случае, если все аргументы Х, участвующие в операции логического отрицания сложения, равны нулю (X1=X2=...=Xn=0).
Логическая функция ложна (Y=0) в том случае, если хотя бы один из аргументов Х, участвующий в операции отрицания сложения – истинен (Хn=1).
Алгебраическая запись операции «ИЛИ-НЕ», образованной от двух аргументов, имеет вид:
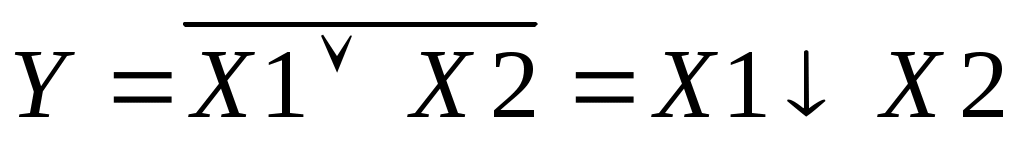
Читается: Функция У равна Х1 «стрелка» Х2.
Знак «↓ » обозначают действие «ИЛИ-НЕ».
Условно-графическое изображение элемента «ИЛИ-НЕ» представлено на рисунке 12.
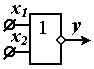
Рисунок 12 - Условно-графическое изображение элемента «ИЛИ-НЕ»
Таблица истинности логического элемента «ИЛИ» имеет вид:
Таблица 19
Свойство операции «ИЛИ-НЕ»: Функция равна «1» только в том случае, если все аргументы, образующие функцию равны «0» (Х1=Х2=0). Если хотя бы один из аргументов «Х», образующий функцию равен «1» (Х1=1 либо Х2=1), то функция обращается в ноль «У=0».
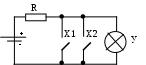
Рисунок 13 – Электрическая схема для элемента «ИЛИ»
Ключи разомкнуты – Х1=Х2=0, лампочка горит – У=1.
Один из ключей замкнут – Х1=1, Х2=0 (либо Х1=0, Х2=1), лампочка гаснет – У=0.
Оба ключа замкнуты - Х1=Х2=1, лампочка гаснет – У=0.
1.2.4 Алгебра логики. Основные законы, теоремы и тождества
Представляет собой свод основных законов, теорем и тождеств, с помощью которых можно упростить любую сложную логическую функцию, а следовательно, схему ЦУ.
* Основные тождества:
для конъюнкции для дизъюнкции
(логического умножения) (логического сложения)
Она задается таблицей истинности приведенной в таблице 13.
Таблица 13 Таблица 14
| X1 | X2 |  | f13=  | | X1 | X2 |  | f11= |
| 0 | 0 | 1 | 1 | | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | | 1 | 1 | 0 | 1 |
f11 = X2 X1
ее значение определяется по формуле f11 =
Функция будет равна “0” только в том случае, когда
X2 = 1; X1 = 0. Во всех остальных случаях функция “истинна” (равна “1”). Таблица приведена в таблице 14.
Логические функции f2 и f4 являются функциями, выполняющими операцию запрета (отрицание импликации).
Логическая функция f2 выполняет операцию запрета по X2 (отрицание импликации f13
). Она задается формулой
f2 = X1 X2=Х1∆Х2
и ее значение определяется как: f2 =
Таким образом, f2 =
. По теореме Моргана доказываем утверждениеf13 =
f2 =
Логическая функция f4 выполняет операцию запрета по X1 (отрицание импликации f11)
f4 = X2 X1=Х2∆Х1
Значение функции в таблице истинности определяется как:
f4 =
Согласно свойств логических функций f4 =
, т.е.f11 =
f4 =
что соответствует исходному значению f4.
Таблицы истинности функций f2 (таблица 15) и f4 (таблица 16) приведены ниже.
Таблица 15 Таблица 16
| X1 | X2 | | f2=  | | X1 | X2 | | f4=  |
| 0 | 0 | 1 | 0 | | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | | 1 | 1 | 0 | 0 |
Удобно все таблицы истинности функций 2-х аргументов представить в виде одной общей таблицы (таблица17). Возле нее указана связь логических функций в виде стрелок. Они указывают на попарную инверсию соответствующих функций.
Таблица 17 – Логические функции 1 и 2 аргументов
| Значение аргументов | Значение Булевых функций | ||||||||||||||||
| X1 | X2 | F0 | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 | F13 | F14 | F15 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| | | 0 | & ∩ | ∆ X1 ← X2 | X1 | ∆ X2← X1 | X2 | ≠ | | | ≡ ∞ | X2 | X2 X1 | X1 | X1 X2 | | 1 |
На рисунке 9 приведены УГО логических элементов для некоторых функций.
Рисунок 9
Рассмотренные логические функции являются элементарными, так как содержат не более одной логической операции. С помощью их можно описать любое логическое устройство и построить его схему.
* Логический элемент «И-НЕ» - элемент ЩЕФФЕРА
Логический элемент «И-НЕ» Выполняет действие логического отрицания умножения аргументов Х1, Х2, ... Хn (отрицание конъюнкции).
Логическая функция принимает значение ложь (Y=0) только в том случае, если все аргументы Х, участвующие в операции логического отрицания умножения, - истинны (Х1=Х2=...=Хn=1).
Если хотя бы один из аргументов Х равен нулю (X=0), то логическая функция Y равна единице (Y=1) - истинна.
Данная функция является сложной. Условно можно считать, что функция состоит из двух операций. Вначале выполняется логическая операция умножения, а затем инверсия.
Алгебраическая запись операции «И-НЕ», образованной от двух аргументов, имеет вид:
Читается: Функция У равна Х1 «штрих» Х2.
Знак « | » обозначают действие «И-НЕ».
Условно-графическое изображение элемента «И-НЕ» представлено на рисунке 10.
Р
исунок 10 - Условно-графическое изображение элемента «И-НЕ»Таблица истинности логического элемента «И-НЕ» имеет вид:
Таблица 18
| Х2 | Х1 | У |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Свойство операции «И-НЕ»: Функция равна «0» только в том случае, если все аргументы, образующие функцию равны «1» (Х1=Х2=1). Если хотя бы один из аргументов «Х», образующий функцию равен «0» (Х1=0 либо Х2=0), то функция обращается в единицу «У=1».
Рисунок 11 – Электрическая схема для элемента «ИЛИ»
Ключи разомкнуты – Х1=Х2=0, лампочка горит – У=1.
Один из ключей замкнут – Х1=1, Х2=0 (либо Х1=0, Х2=1), лампочка горит – У=1.
Оба ключа замкнуты - Х1=Х2=1, лампочка гаснет– У=0.
* Логический элемент «ИЛИ-НЕ» - элемент ПИРСА
Логический элемент «ИЛИ-НЕ» Выполняет действие логического отрицания сложения аргументов Х1, Х2, ... Хn (отрицание дизъюнкции).
Логическая функция истинна (Y=1) только в том случае, если все аргументы Х, участвующие в операции логического отрицания сложения, равны нулю (X1=X2=...=Xn=0).
Логическая функция ложна (Y=0) в том случае, если хотя бы один из аргументов Х, участвующий в операции отрицания сложения – истинен (Хn=1).
Алгебраическая запись операции «ИЛИ-НЕ», образованной от двух аргументов, имеет вид:
Читается: Функция У равна Х1 «стрелка» Х2.
Знак «↓ » обозначают действие «ИЛИ-НЕ».
Условно-графическое изображение элемента «ИЛИ-НЕ» представлено на рисунке 12.
Рисунок 12 - Условно-графическое изображение элемента «ИЛИ-НЕ»
Таблица истинности логического элемента «ИЛИ» имеет вид:
Таблица 19
| Х2 | Х1 | У |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Свойство операции «ИЛИ-НЕ»: Функция равна «1» только в том случае, если все аргументы, образующие функцию равны «0» (Х1=Х2=0). Если хотя бы один из аргументов «Х», образующий функцию равен «1» (Х1=1 либо Х2=1), то функция обращается в ноль «У=0».
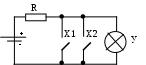
Рисунок 13 – Электрическая схема для элемента «ИЛИ»
Ключи разомкнуты – Х1=Х2=0, лампочка горит – У=1.
Один из ключей замкнут – Х1=1, Х2=0 (либо Х1=0, Х2=1), лампочка гаснет – У=0.
Оба ключа замкнуты - Х1=Х2=1, лампочка гаснет – У=0.
1.2.4 Алгебра логики. Основные законы, теоремы и тождества
Представляет собой свод основных законов, теорем и тождеств, с помощью которых можно упростить любую сложную логическую функцию, а следовательно, схему ЦУ.
* Основные тождества:
для конъюнкции для дизъюнкции
(логического умножения) (логического сложения)